اثر پوستی در مهندسی برق — به زبان ساده
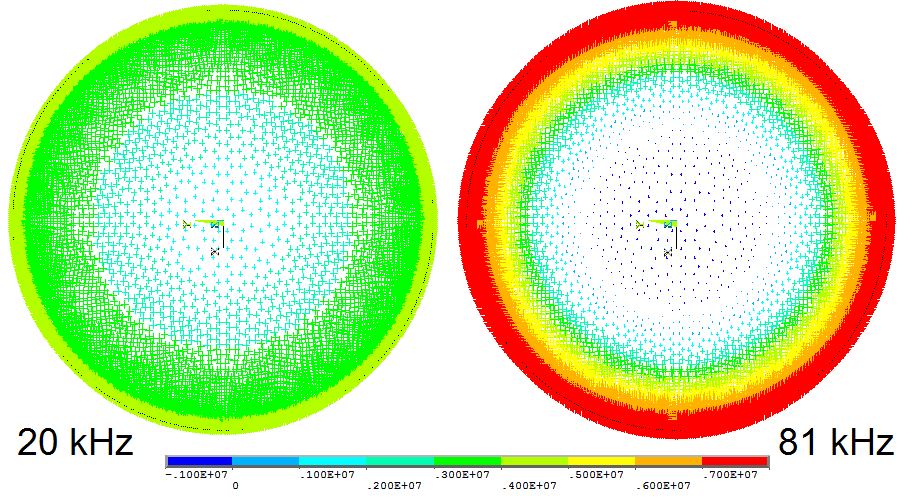
در آموزشهای قبلی مجله فرادرس، درباره گرمایش القایی صحبت کردیم. در این آموزش قصد داریم اثر پوستی یا سطحی در مهندسی برق را بررسی کنیم.
تمایل جریان متناوب الکتریکی (AC) به پخش شدن در داخل هادی الکتریکی، «اثر پوستی» (Skin Effect) نام دارد. چگالی جریان در نزدیکی سطح هادی، به دلیل اثر پوستی، بیشترین مقدار ممکن را دارد. هرچه از سطح به داخل رسانا حرکت کنیم، چگالی جریان کمتر میشود.
جریان الکتریکی، بیشتر از سطح هادی عبور میکند. در واقع این سطح، لایهای بین سطح خارجی رسانا و «عمق نفوذ» (Skin Depth) هادی است. هرچه فرکانس بالاتر باشد، «مقاومت موثر» (Effective Resistance) هادی به دلیل اثر پوستی، بیشتر میشود. با افزایش فرکانس، عمق نفوذ در هادی کاهش مییابد. به این ترتیب، سطح مقطع موثر هادی کم میشود، زیرا جریان از سطح کمتری عبور میکند.
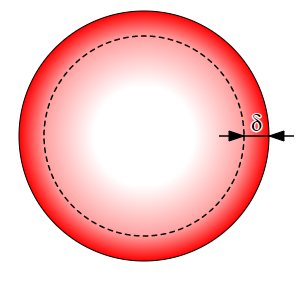
اثر پوستی به دلیل جریانهای گردابی در داخل هادی ایجاد میشود. همانطور که میدانیم، با اعمال یک میدان مغناطیسی متغیر با زمان به هادی، جریانهای گردشی در داخل هادی به وجود میآید. این جریانها طبق قانون لنز با میدان مغناطیسیِ اعمالشده مخالفت میکنند.
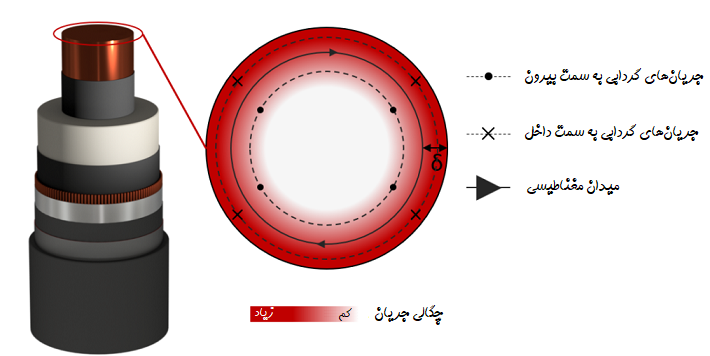
در سیستمهای قدرت، به دلیل وجود اثر پوستی، مقاومت AC سیم زیاد میشود. افزایش مقاومت، مطلوب نیست زیرا تلفات سیستم را افزایش میدهد. این مقاومت را میتوان به وسیله «سیم لیتز بافته شده» (Woven Litz Wire) حذف کرد. در یک سیم استوانهای با قطر زیاد، قسمت داخلی سیم جریان کمی را حمل میکند. به همین دلیل، برای کم کردن وزن و هزینه، میتوان داخل هادی را لولهگذاری کرد.
دلیل پدیده اثر پوستی
همانطور که میدانیم، معمولا برای انتقال انرژی یا سیگنال الکتریکی، از رساناها، مخصوصا رساناهای سیمی استفاده میشود. سیگنال الکتریکی میتواند یک جریان متناوب با زمان باشد. منبع تولید این سیگنال، یک میدان الکتریکی ایجاد میکند. الکترونها یا همان حاملهای بار تشکیلدهنده جریان به وسیله این میدان الکتریکی، وادار به حرکت میشوند و به این ترتیب، جریان از هادی عبور میکند.
جریان الکتریکی متناوب، در داخل و اطراف هادی، یک میدان مغناطیسی متناوب ایجاد میکند. اگر شدت جریان در هادی تغییر کند، میدان مغناطیسی نیز تغییر میکند. طبق قانون لنز، تغییر در میدان مغناطیسی سبب ایجاد میدان الکتریکی میشود. این میدان الکتریکی، با تغییر شدت جریان در هادی مخالفت میکند که «نیروی ضد محرکه الکتریکی» (Counter Electromotive Force) نام دارد. این نیرو در مرکز هادی بیشترین مقدار خود را دارد و به الکترونهای هدایتی واقع در مرکز، نیرویی به سمت سطح هادی وارد میکند. جریان اصلی و جریان گردابی (ناشی از تغییر میدان H) در مرکز هادی یکدیگر را خنثی میکنند و به دلیل اثر پوستی نیرویی در جهت سطح هادی به الکترونها وارد میشود. شکل زیر، این پدیده را نشان میدهد.
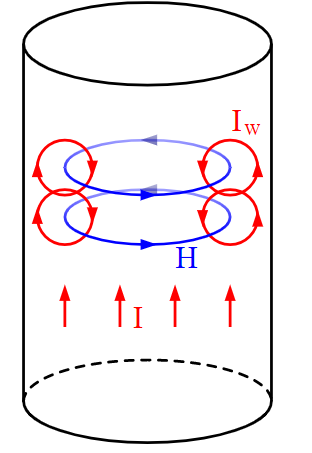
همانطور که گفتیم، طبق قانون القای الکترومغناطیسی، با اعمال یک میدان مغناطیسی متناوب به هادی، میدان الکتریکی در داخل آن القا میشود. بنابراین در حالت کلی، اگر یک میدان الکترومغناطیسی به هادی برخورد کند، در داخل هادی، جریان القا میشود. این پدیده، انعکاس امواج الکترومغناطیسی از فلزات را نشان میدهد.
صرفنظر از اینکه منبع چه توانی به هادی تحویل میدهد، چگالی جریان در سطح هادی بیشترین مقدار خود را دارد. هرچه به عمق هادی نفوذ کنیم، اندازه چگالی جریان کم میشود. این کاهش در چگالی جریان به نام اثر پوستی مشهور است. عمق نفوذ نیز نقطهای است که در آن، چگالی جریان به $$1/e$$ مقدار خود در سطح هادی میرسد. حدود ۶۳ درصد جریان عبوری از هادی از لایهای به ضخامت یک عمق نفوذ ($$\delta$$) و حدود ۹۸ درصد این جریان، از لایهای به ضخامت تقریبا ۴ برابر عمق نفوذ ($$4\delta$$) عبور میکند. بنابراین فقط ۲ درصد از کل چگالی جریان، از قسمتهای داخلی هادی میگذرد. این رفتار با جریان مستقیم متفاوت است. در جریان مستقیم، جریان از سطح مقطع سیم رسانا به صورت یکنواخت عبور میکند (زیرا در جریان مستقیم، فرکانس برابر صفر است).
بنابراین، برای جریان مستقیم گذرنده از یک سیم، میتوان مقاومت سیم را بر حسب طول و قطر آن محاسبه کرد. زیرا در این حالت فرض میشود جریان الکتریکی در سطح مقطع سیم، به صورت یکنواخت توزیع شده است. هرچند، برای جریان متناوب تعامل بین میدان الکتریکی و میدان مغناطیسی در هادی باعث میشود جریان در سطح خارجی سیم توزیع شود. اثر پوستی در فرکانسهای رادیویی باعث میشود جریان، فقط از یک لایه نازک هادی عبور کند.
«هوراس لمب» (Horace Lamb) در سال ۱۸۸۳ برای نخستین بار، اثر پوستی را در مقالهای برای هادیهای کروی ارائه کرد. پس از آن، «اولیور هِویساید» (Oliver Heaviside) در سال ۱۸۸۵، این پدیده را برای هادی با شکلهای مختلف تعمیم داد.

اثر پوستی، در تحلیل و طراحی مدارها در فرکانس مایکروویو و رادیویی، خطوط انتقال (موجبرها) و آنتنها، نقش مهمی دارد. همچنین این پدیده در فرکانس برق شهری و سیستمهایِ توزیع و انتقالِ توانِ الکتریکیِ AC حائز اهمیت است.
فرمول اثر پوستی
هرچه به سمت داخل هادی حرکت کنیم، چگالی جریان ($$J$$)، نسبت به مقدار آن در سطح هادی ($$J_S$$) به صورت نمایی کاهش مییابد. رابطه بین این دو پارامتر به صورت زیر است:
$$J=J_S \, e^{-(1+j)d/\delta}$$
که در آن $$\delta$$، «عمق نفوذ» (Skin Depth) و $$d$$ فاصله از سطح هادی است. به این ترتیب، عمق نفوذ بر حسب فاصلهای از سطح هادی تعریف میشود که در آن چگالی جریان به $$1/e$$ (حدود ۰.۳۷) مقدار خود در سطح هادی ($$J_s$$) میرسد. قسمت موهومی توان نمایی، نشان میدهد که اگر به اندازه یک عمق نفوذ وارد هادی شویم، فاز چگالی جریان به اندازه یک رادیان تاخیر خواهد داشت.
فرمول کلی برای عمق نفوذ به صورت زیر است:
$$\delta=\sqrt{\frac{2\rho}{\omega \mu}} \, \sqrt{\sqrt{1+(\rho \omega \varepsilon)^2}+\rho \omega \varepsilon}$$
که در آن:
- $$\rho$$ مقاومت هادی است.
- $$\omega$$ فرکانس زاویهای جریان و برابر با $$2\pi f$$ است.
- $$\mu = \mu_r \mu_0$$ است که $$\mu_r$$ ضریب نفوذپذیری مغناطیسی نسبی هادی و $$\mu_0$$ ضریب نفوذپذیری خلا هستند.
- $$\varepsilon = \varepsilon_0 \varepsilon_r$$ است که $$\varepsilon_r$$ ضریب گذردهی الکتریکی نسبی هادی و $$\varepsilon_0$$ ضریب گذردهی خلا هستند.
وقتی فرکانس از مقدار $$1/\rho \varepsilon$$ کمتر باشد، عبارت زیر رادیکالِ بزرگ، به عدد یک نزدیک میشود. بنابراین میتوان عمق نفوذ را به صورت ساده زیر نوشت:
$$\delta=\sqrt{\frac{2 \rho}{\omega \mu}}$$
در فرکانسهای پایننتر از فرکانس پلاسمای هادی (وابسته به چگالی الکترونهای آزاد در ماده) یا در فرکانسهایی که هادی، رزونانسهای مولکولی یا اتمی ندارد (در این حالت، قسمت موهومی $$\varepsilon$$ بزرگ است)، رابطه بالا معتبر است. همه این شرایط در مواد با رسانایی خوب مثل فلزات تا فرکانس مایکروویو برقرار است. بنابراین، این رابطه برای فلزات درست است. مثلا برای مس، این رابطه تا فرکانس $$10^{18}$$ هرتز معتبر است. عمق نفوذ برای فلز مس، در فرکانس ۶۰ هرتز، حدوداً ۸.۵ میلیمتر است. در فرکانسهای بالا، عمق نفوذ بسیار کمتر خواهد بود.
در رساناهای ضعیف و در فرکانسهای به اندازه کافی بالا، ضریب زیر رادیکالِ بزرگ، زیاد میشود. در فرکانسهای بسیار بزرگتر از $$1/\rho \varepsilon$$ نشان داده میشود که عمق نفوذ، به صورت مجانبی به مقدار زیر نزدیک خواهد شد:
$$\delta \approx 2\rho \sqrt{\frac{\epsilon}{\mu}}$$
این انحراف از مقدار اصلی، فقط برای مواد با هدایت ضعیف و فرکانسهایی که در آن، اندازه طول موج خلا خیلی بزرگتر از عمق نفوذ نیست، صحیح است. برای مثال، سیلیکون خالص، یک هادی ضعیف است و عمق نفوذ آن در فرکانس ۱۰۰ کیلوهرتز ($$\lambda=3000m$$) حدود ۴۰ متر است. هرچند، با افزایش فرکانس به محدوده مگاهرتز، عمق نفوذ هیچگاه کمتر از مقدار مجانبی خود یعنی ۱۱ متر نخواهد شد. نتیجه آن است که در مواد با هدایت ضعیف مثل سیلیکون خالص، لازم نیست اثر پوستی را در نظر بگیریم. این مسئله به این معنی است که جریان در سطح مقطع ماده - صرفنظر از فرکانس - به طور یکنواخت توزیع شده است.
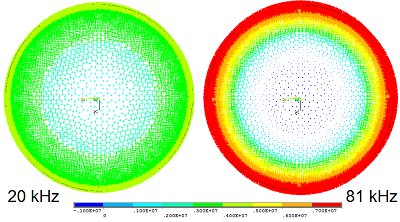
چگالی جریان در یک هادی استوانهای
هنگامی که عمق نفوذ نسبت به شعاع هادی کوچک نباشد، چگالی جریان را میتوان بر حسب توابع بسل بیان کرد. چگالی جریان داخل سیم استوانهای که تحت تاثیر میدانهای دیگر نیست، به صورت تابعی از فاصله از محور هادی و به صورت زیر نوشته میشود:
$$J_r=\frac{kI}{2\pi R} \frac{J_0(kr)}{J_1(kR)}=J_R \frac{kr}{kR}$$
که در آن:
- $$\omega$$ فرکانس زاویهای جریان و برابر با $$2 \pi f$$ است.
- $$r$$ فاصله از محور سیم است.
- $$R$$ شعاع سیم است.
- $$J_r$$ فازور چگالی جریان در فاصله $$r$$ از محور سیم است.
- $$J_R$$ فازور چگالی جریان در سطح سیم است.
- $$I$$ فازور کل جریان است.
- $$J_0$$ تابع بسل نوع اول و از درجه صفر است.
- $$J_1$$ تابع بسل نوع اول و از درجه یک است.
- $$\rho$$ مقاومت هادی است.
- $$\mu_r$$ ضریب نفوذپذیری مغناطیسی نسبی هادی و $$\mu_0$$ ضریب نفوذپذیری مغناطیسی خلا و برابر $$4 \pi \times 10^{-7} H/m$$ است.
- $$\mu = \mu_0 \mu_r$$
عبارت $$k=\sqrt{\frac{-j \omega \mu}{\rho}} =\frac{1-j}{\delta}$$ عدد موج در هادی است. به $$\delta$$، عمق نفوذ نیز میگویند. از آنجا که $$k$$ یک عدد مختلط است، توابع بسل نیز مختلط هستند. دامنه و فاز چگالی جریان با فاصله از سطح هادی تغییر میکند.
امپدانس سیم دایرهای
امپدانس داخلی برای یک سیم دایرهای بر حسب واحد طول (متر) به صورت زیر تعریف میشود:
$$Z_{int}=\frac{k \rho}{2 \pi R} \, \frac{J_0(KR)}{J_1(KR)}$$
این امپدانس یک مقدار مختلط است و از اتصال سری یک مقاومت حقیقی و یک راکتانس موهومی تشکیل میشود که نتیجه «اندوکتانس خودی» (Self-Inductance) سیم نسبت به واحد طول است.
اندوکتانس
قسمتی از اندوکتانس سیم را میتوان به میدان مغناطیسی داخل سیم نسبت داد که به آن، «اندوکتانس داخلی» (Internal Inductance) میگویند. قسمت موهومی امپدانس داده شده در معادله بالا، راکتانس سلفی سیم است. اثرات میدانهای مغناطیسی خارج از سیم که توسط سیم تولید شدهاند، «اندوکتانس خارجی» (External Inductance) را تشکیل میدهد.
در فرکانسهایی که عمق نفوذ نسبت به اندازه هادی، بزرگ نیست، اثر پوستی موجب کاهش اندوکتانس داخلی سیم میشود، در حالی که روی اندوکتانس خارجی تاثیری ندارد. این جزء کوچک از اندوکتانس، در فرکانسهای پایین صرفنظر از شعاع سیم، به عدد $$\frac{\mu}{8 \pi}$$ میل میکند. در شکل زیر اندوکتانس داخلی یک سیم دایرهای بر حسب نسبت عمق نفوذ به شعاع سیم نشان داده است.
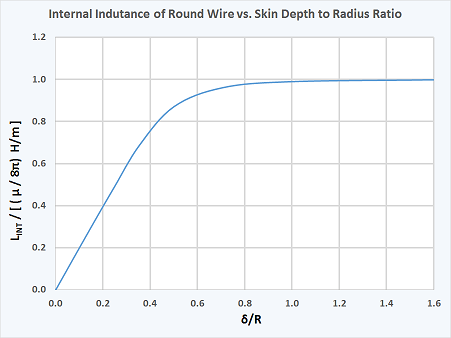
مقاومت
مهمترین نتیجه اثر پوستی روی امپدانس یک سیم تکی، افزایش مقاومت سیم و تلفات منتجه است. عبور جریان محدود در نزدیکی سطح هادی بزرگ (با ضخامت خیلی بزرگتر از $$\delta$$) یک مقاومت موثر ایجاد میکند. اگر جریان عبوری از یک لایه با ضخامت $$\delta$$ به صورت یکنواخت بگذرد، میتوان مقاومت DC در اثر این جریان را با مقاومت موثر جریان در حالت قبل برابر در نظر گرفت.
سطح مقطع موثر، تقریبا برابر با حاصل ضرب $$\delta$$ در محیط هادی است. بنابراین، یک هادی استوانهای بلند مثل سیم، با قطر $$D>>\delta$$، مقاومتی تقریبا برابر با یک لوله خالی حامل جریان مستقیم و با ضخامت $$\delta$$ دارد. مقاومت AC یک سیم با طول L و مقاومت ویژه $$\rho$$ عبارت است از:
$$R\approx \frac{L \rho}{\pi (D- \delta)\delta} \approx \frac{L \rho}{\pi D \delta}$$
در تقریبِ آخر، فرض شده است که $$D>>\delta$$ باشد.
اگر فرض کنیم مقاومت AC یک هادی نسبت به فرکانس f، به دلیل اثر پوستی 10% زیاد شود، فرمول تقریبی قطر سیم ($$D_W$$) با سطح مقطع دایرهای به صورت زیر داده میشود:
$$D_W = \frac{200mm}{\sqrt{f(Hz)}}$$
این معادله، برای افزایش مقاومت AC در یک سیم تکی صحیح است. در صورتی که در نزدیکی این سیم، سیمهای دیگری (مثلا در یک کابل یا سیمپیچ) نیز داشته باشیم، مقاومت AC به وسیله «اثر مجاورت» (Proximity Effect) نیز تحت تاثیر قرار میگیرد که میتواند منجر به افزایش بیشتر مقاومت AC شود.
تاثیر نوع ماده روی اثر پوستی
در یک رسانای خوب، عمق نفوذ با ریشه دوم مقاومت متناسب است. یعنی رساناهای بهتر، عمق نفوذ کمتری دارند. در این رساناها، نسبت مقاومت AC به مقاومت DC بالاتر از سایر رساناهای با مقاومت بالا است. مثلا مقاومت هادی مسی با طول ۱۰۰۰ میلیمتر، در فرکانس ۶۰ هرتز، 23 درصد بیشتر از مقدار آن در فرکانس DC است. در هادی آلومینیومی با اندازه مشابه در فرکانس ۶۰ هرتز، مقاومت AC نسبت به مقاومت DC، فقط ۱۰ درصد بیشتر است.
از سوی دیگر، عمق نفوذ، با جذر ضریب نفوذپذیری مغناطیسی هادی، نسبت عکس دارد. مثلا ضریب هدایت آهن حدودا ۱/۷ ضریب هدایتی مس است. اما به دلیل آنکه آهن مادهای فرومغناطیسی است، ضریب نفوذپذیری آن حدودا ده هزار برابر بزرگتر است. به همین دلیل، عمق نفوذ آهن ۱/۳۸ برابر عمق نفود مس است. این عدد در فرکانس ۶۰ هرتز حدودا ۲۲۰ میکرومتر خواهد بود. به همین دلیل، سیم آهنی برای خطوط انتقال برق AC بسیار نامناسب است. زیرا مقاومت الکتریکی آن زیاد است. اثر پوستی، ضخامت موثر را در ورقه هسته ترانسفورماتورهای توان کاهش میدهد. این موضوع باعث افزایش تلفات ترانسفورماتورها میشود.
میلههای آهنی برای جوشکاری در فرکانسهای DC بسیار مناسب هستند. اما استفاده از آنها برای فرکانسهای خیلی بالاتر از ۶۰ هرتز تقریبا غیرممکن است. در فرکانسهایی در حدود چند کیلوهرتز، افزایش مقاومت AC به دلیل اثر پوستی، باعث داغ شدن میله جوشکاری میشود. به این ترتیب، توان بسیار کمی برای عملیات جوشکاری باقی میماند. برای جوشکاری در فرکانسهای بالا، فقط میلههای غیرمغناطیسی قابل استفاده هستند.
کاهش اثر پوستی
در فرکانسهای پایین بین چند کیلوهرتز تا حدود یک مگاهرتز، برای کم کردن اثر پوستی از یک نوع کابل به نام «سیم لیتز» (Litz wire) استفاده میشود. این سیم، شامل تعدادی رشته سیم عایقدار است که با طراحی دقیقی به یکدیگر بافته شدهاند. بنابراین، میدان مغناطیسی، رفتاری مشابه رفتار روی سیمها دارد. به این ترتیب، توزیع جریان روی سیم یکنواخت است. تاثیر اثر پوستی روی هریک از رشته سیمها بسیار ناچیز است. بنابراین در این سیم، افزایش مقاومت AC روی نخواهد داد (برخلاف یک سیم تکی با قطر مشابه).

در سیمپیچی ترانسفورماتورهای فرکانس بالا، با حذف یا کاهش اثر پوستی و اثر مجاورتی، بازده زیاد میشود. در این حالت، سیم لیتز به کار برده میشود. ترانسفورماتورهای توان بزرگ، از سیم لیتز استفاده میکنند، اما در این ترانسفورماتورها، استفاده از سطح مقطع بزرگتر، منجر به ایجاد اثرات عمق نفوذ بزرگتر در فرکانس برق شهری میشود.
در آنتنها، برای فرکانسهای میانی تا مایکروویو از رشتههای رسانا مانند نانوتیوپهای کربنی استفاده میشود که ابعاد آنها برخلاف هادیهای رشتهای، از عمق نفوذ کمتر است. به این ترتیب، از تمام سطح مقطع رشته سیم استفاده میشود. این موضوع منجر به طراحی آنتنهایی با وزن بسیار کم خواهد شد.

خطوط قدرت ولتاژ و جریان بالا، عموما از کابل آلومینیومی با هستهای از جنس فولاد تقویتشده استفاده میکنند. هسته فولادی، پایینتر از عمق نفوذ قرار دارد و جریان AC از آن عبور نمیکند.
در کاربردهایی که جریان عبوری چندین هزار آمپر است، هادیها جای خود را به لوله میدهند و قسمت داخلی هادی که جریان کمی از آن عبور میکند، کاملا حذف میشود. به این ترتیب، مقاومت AC تغییری نمیکند، اما وزن کلی هادی کاهش قابل ملاحظهای خواهد داشت.
همچنین در کاربردهای جریان بالا که هادیها ضخامتی بین ۵ تا 5۰ میلیمتر دارند (مثل «باسبارهای» (Busbar) تخت یا حلقوی)، اثر پوستی در خمیدگیهای تیز رخ میدهد. در این حالت، فلز در داخلِ خمیدگی فشرده و بیرون آن کشیده میشود. به دلیل آنکه جریان در عبور از خمیدگی سطح کمتری را طی میکند، مقاومت در این محدوده کمتر است. بنابراین، جریان نزدیک به سطح داخلیِ خمیدگی، تمرکز بیشتری دارد. این موضوع باعث میشود افزایش دما در خمیدگیهای هادی نسبت به قسمتهای بدون خمیدگی بیشتر باشد.
اثر پوستی در گوشههای هادی مستطیلی نیز روی میدهد. در این حالت، میدان مغناطیسی در گوشهها نسبت به کنارههای هادی بیشتر متمرکز میشود. این موضوع باعث عملکرد بهتر نسبت به هادیهای نازک و عریض میشود. در این حالت، جریان بالاتر، اما افزایش دما کمتر است. برای مثال، در هادیهای نواری اثرات گوشهها به صورت موثر حذف میشود. بنابراین، میتوان نتیجهگیری کرد که یک ترانسفورماتور با هسته گرد نسبت به ترانسفورماتور معادل با هسته مربعی یا مستطیلی، بازده بهتری دارد.
در هادیهای استوانهای، از پوشش نقره استفاده میشود، زیرا نقره ضریب هدایت بالاتری دارد. از این روش، اغلب در فرکانسهای VHF و مایکروویو استفاده میشود. در این فرکانسها، به دلیل عمق نفوذ کم، به لایه بسیار نازکی از نقره نیاز است. به این ترتیب، بهبود در هدایت، هزینه بسیار پایینی خواهد داشت. از پوشش نقره در سطح موجبرهای مورد استفاده در انتقال امواج مایکروویو نیز استفاده میشود. به این ترتیب، تضعیف امواج منتشر شده به دلیل تلفات مقاومتی ناشی از جریانهای گردابی، کم میشود. در این حالت، اثر پوستی، جریانهای گردابی را به یک لایه بسیار نازک از ساختار موجبر محدود میکند.

از طلا نیز برای پوشش استفاده میشود. اگرچه ضریب هدایتی طلا از مس و نقره کمتر است، اما بر خلاف این دو فلز، طلا زنگ نمیزند. یک لایه نازک از مس یا نقره اکسید شده، هدایت بسیار پایینی دارد و باعث تلفات توان بسیار زیادی میشود، زیرا بیشتر جریان از این لایه عبور میکند.
اخیرا، نشان داده شده است که در کاربردهای فرکانس بسیار بالا، پوششدهی به مواد غیر مغناطیسی و فرومغناطیسی با ضخامت نانومتر، افزایش مقاومتِ ناشی از اثر پوستی را حذف میکند. یک نظریه برای مواد فرومغناطیسی آن است که این مواد در فرکانسهای بسیار بالا، میدانها و جریانهایی تولید میکنند که با میدانها و جریانهای تولید شده توسط مواد غیر مغناطیسی مخالفت میکند. اما برای توجیه این رفتار در مواد فرومغناطیسی، کار بیشتری نیاز است تا مکانیزم دقیق آن مشخص شود. به این طریق میتوان بازده رساناها را برای فرکانسهای چندین گیگاهرتز یا بالاتر افزایش داد. بنابراین، در توسعه ارتباطات نسل پنجم، این راهکار، یکی از روشهای پیشنهادی است.
چند مثال از اثر پوستی
یک رابطه کاربردی برای عمق نفوذ به صورت بیان میشود:
$$\delta = \sqrt{\frac{2 \rho}{(2\pi f)(\mu_0 \mu_r)}} \approx \sqrt{\frac{\rho}{\mu_r f}}$$
که در آن:
- $$\delta$$ عمق نفوذ بر حسب متر است.
- $$\mu_r$$ ضریب نفوذپذیری نسبی ماده است.
- $$\rho$$ مقاومت ویژه ماده با واحد $$\Omega .m$$ و معکوس ضریب هدایتی ماده ($$\rho= \frac{1}{\sigma}$$) است. برای مثال برای فلز مس این عدد برابر $$\rho= 1.68 \times 10^{-8} \Omega . m$$ است.
- $$f$$ نیز فرکانس جریان با واحد هرتز (Hz) است.
طلا یک هادی خوب با مقاومت $$2.44\times 10^{-8} \Omega. m$$ و یک ماده غیر مغناطیسی است. بنابراین برای طلا $$\mu_r=1$$ است. پس عمق نفوذ این هادی برای فرکانس ۵۰ هرتز برابر است با:
$$\delta= 503 \sqrt{\frac{2.44. 10^{-8}}{1.50}}=11.1 mm$$
سرب، برخلاف طلا یک هادی نسبتا ضعیف محسوب میشود. مقاومت سرب برابر $$2.2\times 10^{-7} \Omega . m$$ است. این عدد حدودا ۹ برابر طلا است. عمق نفوذ سرب در فرکانس ۵۰ هرتز حدودا ۳۳ میلیمتر یا $$\sqrt{9}=3$$ برابر طلا است.
موادی که خاصیت مغناطیسی بالایی دارند، به دلیل ضریب نفوذپذیری مغناطیسی ($$\mu_r$$) بزرگ، عمق نفوذ کمی دارند. برای مثال، علیرغم هدایت ضعیفتر آهن، عمق نفوذ در این فلز کمتر است یا در اجاقهای القایی نمیتوان از فولاد ضد زنگ استفاده کرد، زیرا این ماده فرومغناطیسی نیست.
در فرکانسهای بسیار بالا، عمق نفوذ برای هادیهای خوب، عدد بسیار کوچکی است. مثلا برای فلزات معمولی در فرکانس ده گیگاهرتز (ناحیه مایکروویو)، عمق نفوذ از یک میکرومتر کمتر است. این مسئله در جدول زیر نشان داده شده است:
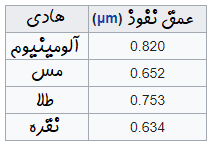
در فرکانسهای مایکروویو، بیشترِ جریان از ناحیه بسیار نازکی از سطح هادی عبور میکند. بنابراین تلفات اهمی موجبرها در فرکانسهای مایکروویو، فقط به پوشش سطحی ماده وابسته است. بنابراین، یک لایه از نقره به ضخامت ۳ میکرومتر که روی یک قطعه شیشه قرار گرفته است، هادی بسیار مناسبی برای این محدوده فرکانسی محسوب میشود.
عمق نفوذ، با ریشه دوم فرکانس نسبت عکس دارد. این مسئله برای فلز مس در زیر نشان داده شده است:
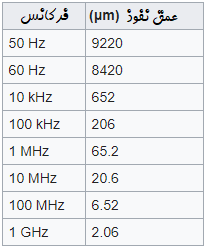
در نمودار شکل زیر، عمق نفوذ بر حسب فرکانس برای مواد مختلف نشان داده شده است (خط قرمز، فرکانس ۵۰ هرتز را نشان میدهد):
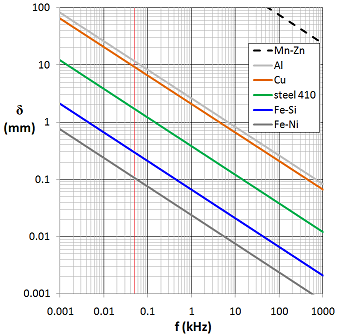
در مهندسی الکترومغناطیس، «هایت» (Hayt) بیان میکند که در یک ایستگاه قدرت، یک باس بار با شعاعی بزرگتر از یک سوم اینچ (۸ میلیمتر) برای جریان متناوب با فرکانس ۶۰ هرتز، اتلاف فلز مس است. در عمل، ضخامت باسبارها برای جریانهای AC بسیار بزرگ، به ندرت از نیم اینچ (۱۲ میلیمتر) بزرگتر میشود. مگر اینکه دلایل مکانیکی باعث افزایش ضخامت باسبار شود.
کاهش اثر پوستی برای اندوکتانس داخلی یک هادی
شکل زیر را در نظر بگیرید. این شکل، هادیهای داخلی و خارجی یک کابل کواکسیال را نشان میدهد.
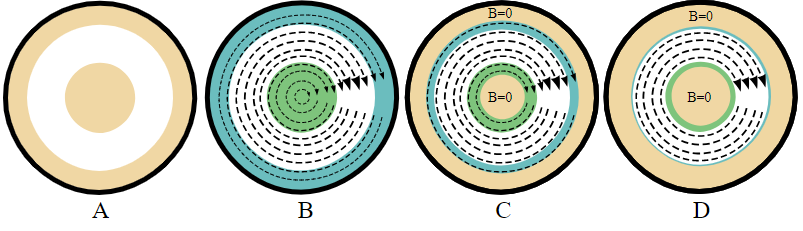
اثر پوستی باعث میشود در فرکانسهای بالا، جریان فقط از سطح هادی عبور کند. به این ترتیب، میدان مغناطیسی داخل سیم کم میشود. نشان داده شده است که این موضوع، اثر کمی بر اندوکتانس خودی سیم دارد. توجه به این نکته ضروری است که اندوکتانس در نظر گرفته شده در این حالت، مربوط به یک هادی تکی است. این اندوکتانس برای یک سیمپیچ که به صورت یک عنصر مداری استفاده میشود، کاربرد ندارد.
قسمت غالب اندوکتانس سیمپیچ، اندوکتانس متقابل بین دورهای سیمپیچ است که به نسبت مربع تعداد دورهای سیمپیچ زیاد میشود. هرچند، وقتی فقط یک سیم را در نظر میگیریم، علاوه بر اندوکتانس خارجی که شامل میدانهای مغناطیسی خارجی سیم است، یک مولفه بسیار کوچکتر نیز وجود دارد که اندوکتانس داخلی سیم را نشان میدهد.
همانطور که گفتیم، اندوکتانس داخلی، ناشی از میدان مغناطیسی داخل سیم است. این مولفه کوچک میدان، با رنگ سبز نشان داده شده است. در فرکانسهای بالا، عمق نفوذ خیلی بزرگتر از شعاع سیم نیست. پس جریان در سطح هادی متمرکز میشود. در این حالت، اندوکتانس خودی سیم کاهش مییابد.
برای یک سیم تکی، هرچه طول سیم نسبت به قطر آن بیشتر باشد، اندوکتانس خودی سیم کاهش قابل ملاحظهای مییابد و برابر صفر در نظر گرفته میشود. هرچند در خطوط انتقال، مقدار میدان مغناطیسی خارجی به دلیل وجود هادی دوم، صرفنظر از طول سیم (و اندوکتانس خودی) کم میشود. بنابراین، اندوکتانس به دلیل اثر پوستی کاهش مییابد، اما هنوز قابل چشمپوشی نیست. برای مثال، در یک جفت سیم پیچیده شده تلفن، اندوکتانس هادیها اساسا با افزایش فرکانس، کاهش مییابد. در این فرکانسها، اثر پوستی مهم میشود. از سوی دیگر، به دلیل شکل سیمپیچ و اندوکتانس متقابل بین دورها، مولفه خارجی اندوکتانس فزایش مییابد. در این حالت، از مولفه داخلی اندوکتانس نیز صرفنظر میشود.
اندوکتانس نسبت به واحد طول برای یک کابل کواکسیال
فرض کنید b ،a و c، به ترتیب، شعاع هادی داخلی، شعاع داخلی هادی بیرونی (پوشش) و شعاع خارجی هادی بیرونی باشند. برای یک جریان، انرژی ذخیره شده در میدانهای مغناطیسی باید با انرژی الکتریکی محاسبه شده مربوط به جریان گذرنده از اندوکتانس کابل کواکسیال برابر باشد. این انرژی، با اندوکتانس اندازهگیری شده از کابل کواکسیال متناسب است.
میدان مغناطیسی داخل کابل کواکسیال را میتوان به سه ناحیه تقسیمبندی کرد. هرکدام از این سه ناحیه، در اندوکتانس الکتریکیِ مشاهده شده از کابل سهم دارند:
- اندوکتانس $$L_{cen}$$ که مربوط به میدان مغناطیسی در ناحیهای با شعاع $$r<a$$ و داخل هادی مرکزی است.
- اندوکتانس $$L_{ext}$$ که مربوط به میدان مغناطیسی در ناحیه $$a<r<b$$ و ناحیه بین دو هادی است (شامل دیالکتریک یا هوا است).
- اندوکتانس $$L_{shd}$$ که مربوط به میدان مغناطیسی در ناحیه $$b<r<c$$ و داخل هادی بیرونی است.
اندوکتانس الکتریکی کل، جمع این سه اندوکتانس است. پس:
$$L_{total}=L_{cer}+L_{shd}+L_{ext}$$
اندوکتانس $$L_{ext}$$ به واسطه اثر پوستی تغییر نمیکند و به وسیله رابطه معروف اندوکتانس کابل کواکسیال به صورت زیر داده میشود:
$$L/D=\frac{\mu_0}{2 \pi}ln \large (\frac {b}{a} \large)$$
که در آن $$L$$، اندوکتانس و $$D$$، طول کابل کواکسیال است.
در فرکانسهای پایین، هر سه اندوکتانس وجود دارند، بنابراین:
$$L_{DC}=L_{cen}+L_{shd}+L_{ext}$$
در فرکانسهای بالا، فقط ناحیه دیالکتریک شار مغناطیسی دارد، پس:
$$L_{\infty}=L_{ext}$$
خطوط انتقال کواکسیال، اغلب برای فرکانسهای بالا مورد استفاده قرار میگیرند. بنابراین تنها معادله آخر معتبر است.
همچنان که اثر پوستی زیاد میشود، جریانهای الکتریکی در سطح خارجی هادی داخلی ($$r=a$$) و سطح داخلی هادی بیرونی ($$r=b$$) متمرکز میشوند. از آنجا که اساسا در عمق هادی داخلی، جریانی موجود نیست، میدان مغناطیسی در درون هادی داخلی وجود ندارد. جریان در هادی داخلی با جریان مخالف گذرنده از سطح داخلی هادی بیرونی، برابر است. بنابراین، در هادی بیرونی ($$b<r<c$$) میدان مغناطیسی وجود ندارد. در فرکانسهای بالاتر، فقط اندوکتانس $$L_{ext}$$، نمایانگر اندوکتانس الکتریکی کل است. اگرچه یک جفت سیمِ پیچیده شده تلفن، شکل متفاوتی دارد، اما اثرات اندوکتانسی آن مشابه است. در فرکانسهای بالاتر، اندوکتانس بیش از ۲۰ درصد کاهش مییابد.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:










سلام ممنون از اموزش خوب شما،پس با توجه به مطالب شما ایا در یک هادی با یک سطح مقطع مشخص جریان dc بیشتر از ac می تواند عبور کند؟