فرادرسآزمون مک نمار (McNemar’s Test) — به زبان ساده
برای آزمون و سنجش ارتباط بین زوج از متغیرهای کیفی، از آزمون مک نمار (McNemar's Test) استفاده می‌شود. بنابراین معمولا زمانی که یک جدول توافقی ۲×۲ از متغیرهای کیفی دو وضعیتی (Dichotomous) در اختیار داریم برای نشان دادن استقلال بین سطرها و ستون‌های این جدول، از آزمون مک نمار کمک می‌گیریم.
این آزمون توسط «کوئین مک‌نمار» (Quinn McNemar) آماردان و روانشناس آمریکایی در سال ۱۹۴۷ معرفی شد. از آنجایی که فرض نرمال بودن در این داده‌ها وجود ندارد، آزمون مک نمار را در گروه آزمون‌ها و روش‌های ناپارامتری در استنباط آماری در نظر می‌گیرند.
برای آشنایی بیشتر با جدول توافقی نوشتار جدول توافقی و کاربردهای آن در SPSS — راهنمای کاربردی را مطالعه کنید. همچنین برای آگاهی با نحوه محاسبات مشابه روی جدول‌های توافقی و آزمون استقلال متغیرهای تصادفی کیفی، خواندن مطلب آزمون نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای۲ نیز توصیه می‌شود.
آزمون مک نمار (McNemar's Test)
آزمون مک نمار بخصوص در تحقیقات و بررسی‌های پزشکی برای سنجش صحت عملکرد یک دارو یا یک نوع تیمار خاص به کار می‌رود و بواسطه آن «حساسیت» (Sensitivity) و «ویژگی» (Specificity) اندازه‌گیری مشخص می‌شود. به این ترتیب می‌توان دقت یک تست را محاسبه کرد. در ادامه هر یک از این مشخصات را در آزمون مک نمار توضیح خواهیم داد.
فرض کنید روی یک گروه از مردم، دو گونه تست و آزمون تشخیصی انجام شده است. می‌خواهیم مطابقت بین این دو آزمون را بسنجیم. به این منظور آزمون را در بین دو گروه بیمار و سالم اجرا کرده‌ایم تا نتایج صحیح و غلط آزمون نیز مشخص شود. تشخیص این که فردی دچار بیماری هست یا خیر، بوسیله متخصص یا علائم بالینی صورت گرفته است که بطور قطع صحیح است. ولی از آنجایی که متخصص در همه جا حضور ندارد، می‌خواهیم به واسطه یک آزمایش شیمیایی، وجود یا عدم وجود بیماری را در فرد تشخیص دهیم.
از آنجایی که این آزمایش دارای دو پاسخ یا مقادیر دو وضعیتی است (بیمار یا سالم) و از طرفی دو نوع آزمون یا تست (نتایج آزمایش شیمیایی و نظر متخصص) نیز داریم، مقدمات اجرای آزمون مک نمار (یک جدول توافقی دو در دو) بوجود آمده است.
جدول توافقی و آزمون مک نمار
با توجه به توضیحات بالا، یک جدول توافقی (Contingency Table) به مانند جدول زیر را در نظر بگیرید. در ستون اول (نظر متخصص)، وضعیت برای آزمون یا تست شماره ۱ نوشته شده و در ستون‌های دوم و سوم نیز وضعیت آزمون یا تست شماره ۲ (آزمایش شیمایی) قرار دارد.
خانه‌هایی که از تقاطع سطر و ستون‌ها حاصل شده، تعداد افرادی است که در آزمون ۱ و ۲ بیمار یا سالم تشخیص داده شده‌اند. برای مثال مقداری که با علامت c مشخص شده، نشان دهنده تعداد افرادی است که در تست ۱ سالم (Negative) ولی در تست یا آزمون ۲، بیمار (Positive) تشخیص داده شده‌اند.
جدول ۱: جدول توافقی آزمون مک نمار
| جدول آزمون مک نمار | جمع سطر | تست ۲ (سالم) | تست ۲ (بیمار) | |
| a+b | b | a | تست ۱ (بیمار) | |
| c+d | d | c | تست ۱ (سالم) | |
| n | b+d | a+c | جمع ستون |
در آزمون مک نمار، فرضیه‌های صفر و مقابل به صورت زیر در نظر گرفته می‌شوند.
- فرض صفر: احتمال حاشیه‌ای برای هر یک از متغیرهای سطری یا ستونی، برابر است.
- فرض مقابل: متغیر سطر با ستون از لحاظ آماری هم‌توزیع نیستند.
اگر $$p_a,p_b,p_c,p_d$$ را احتمالات یا فراوانی نسبی در جدول فراوانی دو طرفه (جدول توافقی) در نظر بگیریم، فرض صفر را در این آزمون، می‌توان به صورت زیر نشان داد.
$$\large {\begin{aligned}H_{0}&:~p_{b}=p_{c}\\H_{1}&:~p_{b}\neq p_{c}\end{aligned}}$$
که در آن $$p_a+p_b= p_a+p_c,\;\;\;p_c+p_d=p_b+p_d$$ است. زیرا در صورتی که متغیر سطر و ستون هم‌توزیع باشند، احتمال آنکه کسی در آزمون ۱ نتیجه مثبت بگیرد باید با احتمال نتیجه مثبت در آزمون ۲ نیز برابر باشد. یعنی نسبت $$\dfrac{a+b}{n}$$ با نسبت $$\dfrac{a+c}{n}$$ یکسان باشد، پس خواهیم داشت:
$$\large p_a+p_b = p_a+p_c$$
و
$$\large p_c+p_d = p_b+p_d$$
آماره آزمون مک نمار
توجه داشته باشید که آماره مک نمار براساس یک جدول توافقی ۲×۲ ساخته می‌شود. در نتیجه اگر جدول ۱ را در نظر گرفته باشیم، آماره آزمون مک نمار به صورت زیر محاسبه می‌شود.
$$\large \chi ^{2}={(b-c)^{2} \over b+c}$$
رابطه ۱
این آماره، دارای توزیع کای ۲ با یک درجه آزادی (Degree of Freedom) است. در نتیجه اگر صورت به اندازه کافی بزرگ باشد، بطوری که اختلاف بین تعداد تشخیص غلط در تست ۲ نسبت به آزمون ۱ با تعداد تشخیص غلط در آزمون ۱ نسبت به آزمون ۲، زیاد باشد، رای به تفاوت بین این دو آزمون خواهیم داد و فرض صفر که یکسان بودن هر دو آزمون را در نظر گرفته بود، رد می‌کنیم.
مقدار بزرگی آماره آزمون بستگی به میزان خطا و سطح آزمون ($$\alpha$$) دارد. به این ترتیب قاعده‌ای را برای این آزمون در نظر می‌گیریم. اگر $$\chi^2 > \chi^2_{(\alpha/2,1)}$$، آنگاه فرض صفر را رد می‌کنیم. در غیر اینصورت دلیلی بر رد صفر وجود ندارد.
مثال ۱
قرار است اثر یک دارو را روی یک بیماری مورد بررسی قرار دهیم. قبل از تجویز دارو وجود بیماری را در دسته‌ای از افراد مورد بررسی قرار می‌دهیم. فراوانی این افراد در سطرها یک جدول توافقی قرار گرفته است. پس از مصرف دارو نیز وجود بیماری را در بین آن‌ها آزمایش کرده‌ایم. می‌خواهیم اثر دارو در بین بیماران را بررسی کنیم. توجه داشته باشید که بیماران قبل و بعد از مصرف دارو مورد آزمایش قرار گرفته‌اند.
| جمع سطر | بعد از مصرف (سالم) | بعد از مصرف (بیمار) | |
| 222 | 121 | 101 | قبل از مصرف (بیمار) |
| 92 | 33 | 59 | قبل از مصرف (سالم) |
| 314 | 154 | 160 | جمع ستون |
مطابق با رابطه ۱، آماره آزمون به صورت زیر محاسبه می‌شود.
$$\large \chi ^{2}={(121-59)^{2} \over {121+59}}=21.35$$
با توجه به اینکه مقدار آماره کای ۲ با یک درجه آزادی تقریبا برابر با ۰٫004 است، فرض صفر رد خواهد شد.
$$\large 21.35 > 0.004$$
به این ترتیب مشخص است که مصرف دارو روی بهبود بیماران تاثیر گذار است. در صورتی که فرض صفر رد نمی‌شد، به این معنی بود که دارو در درمان بیماری، بی‌اثر است.
توزیع دو جمله‌ای برای آماره آزمون مک نمار
اگر مقدار b و c کوچک باشد بطوری که مجموع آن‌ها از ۲۵ کوچکتر باشد، تقریب توزیع کای برای توزیع آماره آزمون مک نمار صحیح نخواهد بود و بهتر است از «توزیع دو جمله‌ای» (Binomial Distribution) و «آزمون دو جمله‌ای» (Binomial Test) استفاده کرد.
در این حالت آماره آزمون را آماره دقیق دو جمله‌ای (Exact Binomial Test) می‌نامند.
توجه داشته باشید که در اینجا منظور از $$n$$، مجموع $$b$$ و $$c$$ است. به این ترتیب، مقدار احتمال (p-Value) برای این آزمون برابر است با:
$$\large {\displaystyle {\text{exact-P-value}}=2\sum _{i=b}^{n}{n \choose i}0.5^{i}(1-0.5)^{n-i},} \;\;\;n = a+b$$
واضح است که این مقدار، دو برابر مقدار بالایی تابع احتمال تجمعی توزیع دو جمله‌ای با پارامترهای $$0.5$$ و $$n$$ است.
نکته: به منظور اصلاح پیوستگی برای توزیع دو جمله‌ای، ادواردز (Edwards) آماره زیر را پیشنهاد کرده است.
$$\large \chi ^{2}={(|b-c|-1)^{2} \over b+c}$$
مثال ۲
با توجه به جدول مربوط به مثال ۱، جدول توافقی زیر را در نظر بگیرید.
| جمع سطر | بعد از مصرف (سالم) | بعد از مصرف (بیمار) | |
| 65 | 6 | 59 | قبل از مصرف (بیمار) |
| 96 | 80 | 16 | قبل از مصرف (سالم) |
| 161 | 86 | 75 | جمع ستون |
هر چند تعداد نمونه‌ها در این جدول کوچک نیست (تعداد موارد مشاهده شده، ۱۶۱ مورد است) ولی تعداد $$c$$ و $$b$$ و بخصوص مجموعشان از ۲۵ (که معمولا برای شرط نرمال بودن در نظر گرفته می‌شود)، کوچکتر است. در نتیجه باید از آزمون دقیق دو جمله‌ای استفاده شود.
مقدار احتمال برای آزمون مک نمار با توزیع دو جمله‌ای، برابر با 0٫053 و با تصحیح پیوستگی ادواردز 0٫055 است که هر دو روش، بدون رد فرض صفر عمل می‌کنند، در حالیکه براساس آزمون مک نمار با توزیع آماره کای ۲، مقدار احتمال برابر با 0٫033 است که در نتیجه فرض صفر را رد می‌کند.
مزایا و معایب آزمون مک نمار
نکته جالب در محاسبه و تفسیر آزمون مک نمار آن است که عناصر قطر اصلی در جدول توافقی نقشی در آماره آزمون و نتیجه آن ندارند. به این معنی که شرایط قبل از درمان در نتایج آزمون اهمیت نداشته و بی‌تاثیر هستند. همانطور که دیده شد، با کوچک بودن مقادیر$$b$$ و $$c$$، توان آزمون به شدت کاهش یافته و ممکن است حتی با بزرگ بودن اندازه نمونه، نتایج نادرستی از آزمون مک نمار گرفته شود.
صحت، حساسیت و ویژگی در جدول‌های توافقی
اصطلاحات زیر را در نظر بگیرید:
- بیمار: کسی که دچار بیماری است.
- سالم: فردی که دچار بیماری نیست.
- مثبت صحیح (True Positive): وضعیتی که فردی بوسیله آزمون به درستی بیمار تشخیص داده شده و نتیجه تست پزشکی روی او، تشخیص بیماری است؛ او واقعا بیمار است.
- منفی صحیح (True Negative): وضعیتی است که فردی بوسیله آزمون سالم تشخیص داده شده در حالیکه در حقیقت نیز سالم است.
- منفی کاذب (False Negative): وضعیتی است که فرد بوسیله آزمون سالم تشخیص داده شده ولی در حقیقت دچار بیماری است. این وضعیت به عنوان خطای آزمون یا تشخیص پزشکی سنجیده می‌شود.
- مثبت کاذب (False Positive): وضعیتی است که فرد بوسیله آزمون بیمار تشخیص داده شده در حالیکه در حقیقت سالم است. این وضعیت نیز به عنوان خطای آزمون یا تشخیص پزشکی در نظر گرفته می‌شود.
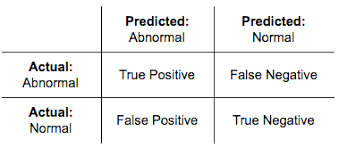
به این ترتیب اگر جدول توافقی را براساس مقایسه نتایج یک آزمون پزشکی با واقعیت ایجاد کنیم، خواهیم داشت:
جدول 2: جدول توافقی و خطای آزمون پزشکی
| حساسیت /
ویژگی/ دقت | جمع سطر | نتیجه تست = سالم | نتیجه تست = بیمار | حقیقت |
| a+b | b | a | بیمار | |
| c+d | d | c | سالم | |
| n | b+d | a+c | جمع ستون |
حال با مقایسه مشخصات این جدول خواهیم داشت:
- a = مثبت صحیح
- b = منفی کاذب
- c = مثبت کاذب
- d = منفی صحیح
در اینجا منظور از صحت در آزمون پزشکی، توانایی آن در تشخیص صحیح فرد بیمار و فرد سالم است. در نتیجه نسبت زیر را صحت (Accuracy) می‌نامیم.
$$\large \operatorname{Accuracy}=\dfrac{a+d}{a+c+b+d}$$
در این حالت حساسیت (Sensitivity) بوسیله رابطه زیر اندازه‌گیری می‌شود.
$$\large \operatorname{Sensitivity}=\dfrac{a}{a+c}$$
به این ترتیب، توانایی یک آزمون پزشکی برای پیدا کردن موارد بیماری بدست می‌آید.
از طرفی ویژگی که به نوعی دقت آزمون پزشکی برای پیدا کردن افراد غیربیمار است، توسط رابطه زیر بدست می‌آید.
$$\large \operatorname{Specificity}=\dfrac{d}{d+b}$$
مثال ۳
فرض کنید یک آزمون پزشکی، قادر است ۲۵ مورد از ۵۰ فرد سالم را به درستی تشخیص دهد و بقیه را به اشتباه، بیمار تشخیص می‌دهد. از طرفی در بین ۱۰۰ بیمار، همه آن‌ها را به درستی بیمار تشخیص داده است. در این صورت جدول توافقی به صورت زیر در خواهد آمد.
| جمع سطر | نتیجه آزمون = سالم | نتیجه آزمون = بیمار | |
| 50 | 0 | 50 | بیمار |
| 50 | 25 | 25 | سالم |
| 100 | 25 | 75 | جمع ستون |
با توجه به روابطی که برای سنجش صحت، حساسیت و ویژگی آزمایش‌های پزشکی گفتیم، خواهیم داشت:
$$\large \operatorname{Accuracy}=\dfrac{50+25}{100}=0.75$$
در نتیجه در ۷۵٪ موارد، این آزمون نتیجه درست را در برخواهد داشت و بیمار را به درستی بیمار و فرد سالم را به درستی، سالم معرفی خواهد کرد.
از طرفی برای محاسبه حساسیت نیز فرمول زیر را به کار می‌بریم:
$$\large \operatorname{Sensitivity}=\dfrac{50}{50+0}=1$$
در نتیجه این آزمون برای تشخیص بیماران، صد در صد، درست عمل می‌کند.
ولی با توجه به این که از بین ۵۰ فرد سالم، نیمی از آن‌ها را بیمار تشخیص داده است، ویژگی آن برابر با ۵۰٪ است.
$$\large \operatorname{Specificity}=\dfrac{25}{25+25}=0.5$$
خلاصه و جمع‌بندی
در این نوشتار به بررسی آزمون مک نمار و خصوصیات آن پرداختیم. البته زمانی که اندازه مشاهدات در گروه‌های با اهمیت کم بود از آزمون با توزیع دو جمله‌ای استفاده کردیم. همچنین به ضعف این آزمون نیز اشاره‌ای داشتیم.
در بررسی و مقایسه نتایج آزمایش‌های پزشکی، بخصوص در اندازه‌گیری صحت و دقت در چنین آزمایش‌های، از آزمون مک نمار و مفاهیم مثبت درست و منفی کاذب استفاده شده و حساسیت و ویژگی آزمون‌های پزشکی اندازه‌گیری می‌شود.
خوشبختانه محاسبه مربوط به این آزمون توسط بیشتر نرم‌افزارهای محاسبات آماری، صورت گرفته و کاربران و محققین آماری، این گونه محاسبات را با دقت و سرعت زیادی انجام داده و به نتیجه مورد نظر می‌رسند.
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
