روش پوسته استوانه ای — از صفر تا صد

«روش پوسته ای» (Shell Method) یا روش پوسته استوانهای روشی برای یافتن حجمهای حاصل از دوران است. در این روش، به جای برشها یا اصطلاحاً قاچهای افقی، برشهای عمودی نواحی با هم جمع شده و سبب میشوند بسیاری از مسائل را که در آنها توصیف برشهای عمودی سادهتر است، آسانتر کرد.
روش پوسته استوانهای روشی برای یافتن حجم با تجزیه یک حجم حاصل از دوران به پوستههای استوانهای است. ناحیهای را در صفحه در نظر بگیرید که به نوارهای عمودی نازک تقسیم شده است. اگر هر نوار عمودی حول محور $$ x $$ چرخانده شود، آنگاه نوار عمودی یک دیسک یا قرص ایجاد خواهد کرد. حال اگر این نوار عمودی حول محور $$ y $$ بچرخد، یک جسم دورانی جدید به دست خواهد آمد که شبیه یک پوسته استوانهای یا یک قوطی خالی بدون سر و ته است. حجم حاصل از پوسته استوانهای برابر با حاصلضرب مساحت سطح استوانه در ضخامت دیواره آن است:
$$ \large \Delta V = 2 \pi x y \Delta x . $$
روش پوسته استوانهای
حجم کل جسم حاصل از دوران را با جمع کردن حجمهای همه این پوستههای استوانهای به ضخامت $$ \Delta x $$ و با میل ضخامت به $$ 0 $$ محاسبه میکنند:
$$ \large V = \int d V = \int _ a ^ b 2 \pi x y \, d x = \int _ a ^ b 2 \pi x f ( x ) \, d x . $$
توجه کنید که محور چرخش و متغیر انتگرالگیری با هم متفاوت هستند، یعنی حتی اگر حول محور $$ x $$ انتگرالگیری کنیم، در حقیقت حول محور $$ y $$ میچرخیم.
در چه مواردی از روش پوسته ای استفاده میکنیم؟
مواردی وجود دارد که در آنها تمایز بین روش قرصی یا دیسک و روش پوسته ای دشوار است. بسیاری از افراد به روش پوسته ای علاقهای ندارند، زیرا درک نمیکنند در این روش چه اتفاقی رخ میدهد. بنابراین، آنها سعی میکنند اغلب از روش قرصی استفاده کنند.
با این حال، مواردی وجود دارد که روش پوسته استوانهای بسیار ساده تر است:
- وقتی تابع $$ f ( x ) $$ حول محور $$ y $$ میچرخد.
- وقتی نمودار دوران یافته حول محور $$ x$$، تابعی از $$ x $$ نباشد، اما تابعی از $$ y $$ باشد.
- وقتی انتگرالگیری از $$ f ( x ) ^ 2 $$ نسبت به انتگرالگیری از $$ x f ( x ) $$ سادهتر باشد (به ویژه انتگرالگیری جزء به جزء).
در ادامه، مثالهایی را از این موارد بررسی میکنیم.
مثالها
در این بخش چند مثال متنوع را بررسی میکنیم.
مثال ۱
با استفاده از روش پوسته استوانهای حجم حاصل از دوران ناحیه محصور به $$ y = \frac { 1 } { x } $$، $$ y = 0 $$، $$ x = 1 $$ و $$ x = 4 $$ حول محور $$ y $$ را محاسبه کنید.
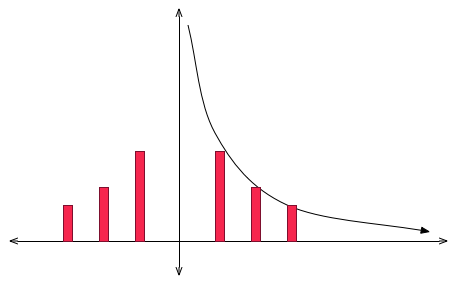
حل: در این حالت، شعاع پوسته استوانهای $$ x $$ و ارتفاع آن $$ y = \frac { 1 } { x } $$ است. از آنجا که نقاط ابتدا و انتهای بازه $$ x $$ برابر با $$ x = 1 $$ و $$ x = 4 $$ هستند، حجم جسم به صورت زیر محاسبه میشود:
$$ \large \begin {aligned} V & = \int _ 1 ^ 4 2 \pi x \cdot \frac { 1 } { x } d x \\ & = 2 \pi \int _ 1 ^ 4 1 d x \\ & = 2 \pi \left [ x \right ] ^ 4 _ 1 \\ & = 2 \pi ( 4 - 1 ) \\ & = 6 \pi . \end {aligned} $$
مثال 2
با استفاده از روش پوسته استوانهای حجم حاصل از دوران ناحیه محدود به $$ y = x $$ و $$ y = x ^ 2 $$ را حول محور $$ y $$ به دست آورید.
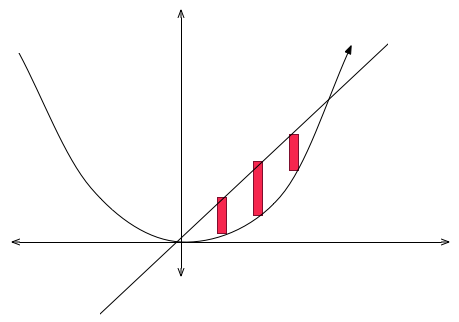
حل: این دو نمودار در نقاط $$ ( 0 , 0 ) $$ و $$ ( 1 , 1 ) $$ تقاطع دارند. شعاع پوسته استوانهای برابر با $$ x $$ بوده و ارتفاع آن $$ x - x ^ 2 $$ است. بنابراین، حجم جسم برابر است با:
$$ \large \begin {aligned} \int _ 0 ^ 1 2 \pi x ( x - x ^ 2 ) \, d x & = \int _ 0 ^ 1 2 \pi ( x ^ 2 - x ^ 3 ) \, d x \\ & = \left [ 2 \pi ( \frac { x ^ 3 } { 3 } - \frac { x ^ 4 } { 4 } ) \right ] _ 0 ^ 1 \\ & = \frac { \pi } { 6 } . \end {aligned} $$
مثال ۳
با استفاده از روش پوستهای حجم کرهای به شعاع $$ r $$ را به دست آورید که حفرهای به شعاع $$ a < r $$ در مرکز آن ایجاد شده است.
حل: شعاع پوسته استوانهای $$ 2 \pi x $$ و ارتفاع آن $$ 2 y = 2 \sqrt { r ^ 2 - x ^ 2 } $$ است. در نتیجه، حجم پوسته استوانهای برابر است با:
$$ \large \Delta V = 2 \pi x ( 2 y ) \Delta x = 4 \pi x \sqrt { r ^ 2 - x ^ 2 } \Delta x . $$
حال، از آنجا که یک سوراخ عمودی به شعاع $$ a $$ در مرکز داریم، نقاط ابتدایی و انتهایی بازه $$ x $$، به ترتیب، $$ x = a $$ و $$ x = r $$ خواهند بود و داریم:
$$ \large \begin {aligned} V & = \int _ a ^ r 4 \pi x \sqrt { r ^ 2 - x ^ 2 } d x \\ & = - \left [ \frac { 4 \pi } { 3 } ( r ^ 2 - x ^ 2 ) ^ { 3 / 2 } \right ] ^ { r } _ a \\ & = \frac { 4 \pi }{ 3 } \left ( r ^ 2 - a ^ 2 \right ) ^ { 3 / 2 } . \end {aligned} $$
مثال ۴
وقتی تابع $$ f ( x ) $$ حول محور $$ y $$ میچرخد، روش پوسته ای یک جواب مستقیم ارائه خواهد داد، اما روش قرصی مستلزم پی بردن به این موضوع است که چگونه حجم مربوطه را محاسبه کنیم. وقتی ناحیه محدود به $$ y = \sqrt { x } $$، خط $$ x = 1 $$ و محور $$ x $$، حول محور $$ y $$ بچرخند، اندازه حجم جسم حاصل را به دست آورید.
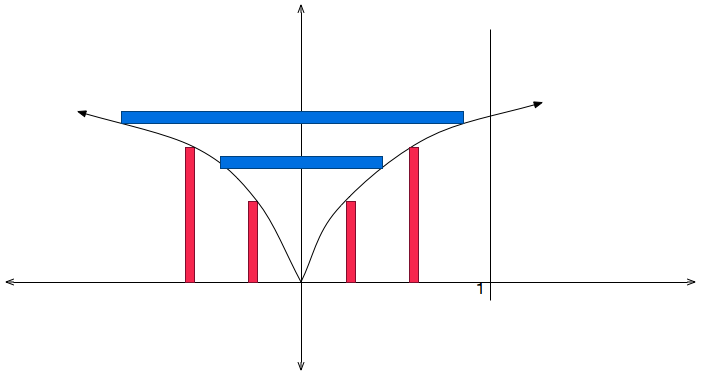
حل: با استفاده از روش پوستهای، وقتی $$ x $$ از $$ 0 $$ تا $$ 1 $$ تغییر میکند، شعاع $$ x $$ و ارتفاع $$ \sqrt { x } $$ است. بنابراین، حجم برابر است با:
$$ \large \int _ 0 ^ 1 2 \pi x \sqrt { x } \, d x = \left [ 2 \pi \times \frac { 2 } { 5 } x ^ { \frac { 5 } { 2 } } \right ] _ 0 ^ 1 = \frac { 4 \pi } { 5 } . $$
اگر از روش قرصی استفاده میکردیم، باید استوانه را با چرخش مربع واحد و سپس تفریق ناحیه محدود به $$ y = 1 $$، $$ y = \sqrt { x } $$ و محور $$ y $$ که حول محور $$ y $$ چرخیده است به دست میآوردیم:
$$ \large \pi \times 1 ^ 2 \times 1 - \int _ 0 ^ 1 \pi x ^ 2 \, d y = \pi - \int _ 0 ^ 1 \pi y ^ 4 \, d y = \pi - \left [ \pi \frac { y ^ 3 } { 5 } \right ] _ 0 ^ 1 = \frac { 4 \pi } { 5 } . $$
مثال ۵
وقتی نمودار دوران یافته حول محور $$ x$$، تابعی از $$ x $$ نباشد، اما تابعی از $$ y $$ باشد، روش پوسته ای یک نتیجه مستقیم خواهد داشت، اما در روش قرصی باید همه توابع مربوطه را محاسبه کنیم. حجم جسم حاصل از دوران ناحیه محدود به $$ x = y ^ 2 - 4 y + 4 $$، $$ x = 0 $$ و $$ x = 1 $$ را که حول محور $$ x $$ میچرخد، محاسبه کنید.
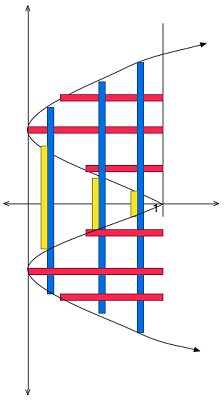
حل: وقتی $$ x = 0 $$ باشد، $$ y = 2 $$ بوده و وقتی $$ x = 1 $$ باشد، $$ y = 1, 3 $$ است. همچنین، وقتی $$ x $$ از $$ 0 $$ تا $$ 1 $$ تغییر میکند، $$ y $$ نیز از $$1$$ تا $$ 3 $$ تغییر خواهد کرد. توجه کنید که تابعی برحسب $$ y $$ داریم. با استفاده از روش پوستهای، وقتی $$ y $$ از $$ 1 $$ به $$ 3 $$ تغییر میکند، شعاع استوانه $$ y$$ و ارتفاع آن $$ 1 - x $$ است. بنابراین، حجم برابر است با:
$$ \large \begin {aligned} \int _ 1 ^ 3 2 \pi y ( 1 - x ) \, d y & = \int _ 1 ^ 3 2 \pi y ( 1 - y ^ 2 + 4 y - 4 ) \ d y \\ & = \int _ 1 ^ 3 2 \pi ( - y ^ 3 + 4 y ^ 2 - 3 y ) \, d y \\ & = \left [ 2 \pi \left ( - \frac { y ^ 4 } { 4 } + \frac { 4 y ^ 3 } { 3 } - \frac { 3 y ^ 2 } { 2 } \right ) \right ] _ 1 ^ 3 \\ & = \frac { 1 6 \pi }{ 3 } . \end {aligned} $$
اگر از روش قرصی استفاده میکردیم، باید باید حجم تولیدی «بالای منحنی» را در نظر میگرفتیم و سپس حجم تولیدی «پایین منحنی» را از آن کم میکردیم. برای این کار توابع $$ x = ( y - 2 ) ^ 2 $$ یا $$ \pm \sqrt { x} = y - 2 $$، بنابراین، $$ y =2 \pm \sqrt { x } $$ را حساب کنیم که منحنی بالا $$ y = 2 + \sqrt { x } $$ و منحنی پایین $$ y = 2 - \sqrt { x } $$ است.
در نتیجه، حجم مورد نظر برابر است با:
$$ \large \begin {aligned} \int _ 0 ^ 1 \pi ( 2 + \sqrt { x } ) ^ 2 \, d x - \int _ 0 ^ 1 \pi ( 2 - \sqrt { x } ) ^ 2 \, d x & = \int _ 0 ^ 1 \pi 8 \sqrt { x } \, d x \\ & = \left [ \frac { 1 6 \pi } { 3 } x ^ { \frac { 3 } { 2 } } \right ] _ 0 ^ 1 \\ & = \frac { 1 6 } { 3 } . \end{aligned} $$
مثال ۶
از روش پوسته ای برای محاسبه حجم حاصل از دوران ناحیه محدود به $$ y = \sqrt { x - 1 } $$، $$ y = 0 $$ و $$ x = 1 0$$ حول خط $$ y = 5 $$ استفاده کنید.
حل: از آنجا که ناحیه دوران یافته حول $$ y = 5 $$ است، پوستههای استوانهای را با خط محور مرکزی $$ y = 5 $$ در نظر میگیریم. در نتیجه، شعاع پوسته استوانهای $$ 2 \pi ( 5 - y ) $$، ارتفاع پوسته استوانهای $$ 10 - x $$ و حجم آن به صورت زیر است:
$$ \large \Delta V = 2 \pi ( 5 -y ) ( 1 0 - x ) \Delta y = 2 \pi ( 5 -y ) ( 1 0 - y ^ 2 - 1 ) \Delta y . $$
از آنجا که نقاط ابتدا و انتهای بازه $$ y = 0 $$ و $$ y = \sqrt { 10 - 1 } = 3 $$ هستند، حجم برابر خواهد بود با:
$$ \large \begin {aligned} V & = \int _ 0 ^ 3 2 \pi ( 5 - y ) ( 1 0 - y ^ 2 - 1 ) \, d y \\ & = \int _ 0 ^ 3 2 \pi ( 5 - y ) ( 9 - y ^ 2 ) \, d y \\ & = \int _ 0 ^ 3 2 \pi ( 4 5 - 9 y - 5 y ^ 2 + y ^ 3 ) \, d y \\ & = 2 \pi \left [ 4 5 y - \frac { 9 } { 2 } y ^ 2 - \frac { 5 } { 3 } y ^ 3 + \frac { y ^ 4 } { 4 } \right ] ^ 3 _ 0 \\ & = 2 \pi \left ( 4 5 \cdot 3 - \frac { 9 } { 2 } \cdot 9 - \frac { 5 } { 3 } \cdot 2 7 + \frac { 8 1 } { 4 } \right ) \\ & = \frac { 2 7 9 \pi } { 2 }. \end{aligned} $$
مثال ۷
حجم جسم حاصل از دوران ناحیه محدود به $$y = 0 $$، $$ y = 1 / (1+ x ^ 2 )$$، $$ x = 0 $$ و $$ x = 1 $$ را حول محور $$ y $$ به دست آورید.
حل: این ناحیه در شکل زیر نشان داده شده است. خط موازی با محور دوران یک پوسته است که حول محور $$ y $$ خواهد چرخید (یک عنصر دیفرانسیلی).
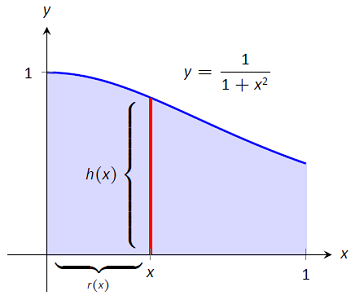
فاصله این خط از محور دوران را $$ r ( x ) $$ مینامیم که در واقع، $$ r ( x ) = x $$ است. ارتفاع نیز $$ h ( x ) $$ است. قسمت بالای خط در $$ y=1/(1+x^2) $$ و قسمت پایینی آن در $$ y = 0 $$ قرار دارد. بنابراین، $$h(x) = 1/(1+x^2)-0 = 1/(1+x^2) $$ است. ناحیه از $$ x = 0 $$ تا $$ x = 1 $$ محدود شده است و حجم مورد نظر برابر است با:
$$ \large V = 2 \pi \int _ 0 ^ 1 \dfrac { x } { 1 + x ^ 2 } \ d x . $$
برای حل این انتگرال از تغییر متغیر $$ u = 1 + x ^ 2 $$ و در نتیجه، $$ d u = 2x d x $$ استفاده میکنیم. در نتیجه، محدوده از $$ u ( 0 ) = 1 $$ تا $$ u ( 1 ) = 2 $$ تغییر میکند. بنابراین، خواهیم داشت:
$$ \large \begin {align*} V & = \pi \int _ 1 ^ 2 \dfrac { 1 } { u } \ du \\[5pt] &= \pi \ln u \Big | _ 1 ^ 2 \\[5pt] & = \pi \ln 2 - \pi \ln 1 \\[5pt] & = \pi \ln 2 \approx 2 . 1 7 8 \ .\end{align*}$$
مثال ۸
حجم جسم حاصل از دوران ناحیه مثلثی با رئوس $$ (0,1)$$، $$(1,1)$$ و $$(1 , 3 )$$ را حول خط $$ x = 3 $$ بیابید.
حل: این ناحیه در بخش (الف) شکل زیر نشان داده شده است. همچنین، عنصر دیفرانسیلی موازی با محور دوران در نظر گرفته شده است. در بخش (ب) از شکل، میبینیم که پوسته با عنصر دیفرانسیلی ردیابی میشود و در بخش (ج) کل جسم نشان داده شده است.
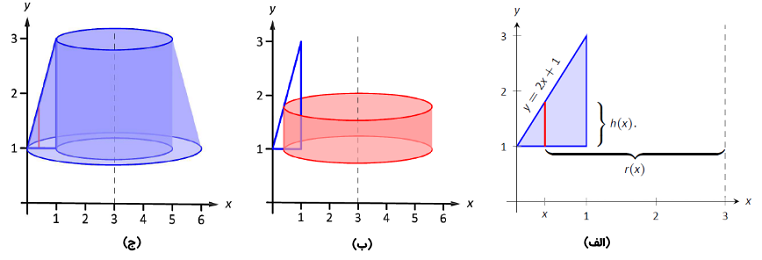
ارتفاع عنصر دیفرانسیلی برابر با فاصله $$ y = 1 $$ از $$ y = 2 x + 1 $$ (خط متصل کننده $$ (0 , 1 )$$ و $$ ( 1 , 3 ) $$) است. بنابراین، $$h(x) = 2x+1-1 = 2x $$. شعاع پوسته که از عنصر دیفرانسیلی تشکیل شده است، اندازهاش از $$ x $$ تا $$ x = 3 $$ است و در نتیجه $$ r ( x ) = 3 - x $$. محدوده $$ x $$ از $$ x = 0 $$ تا $$ x = 1 $$ تغییر میکند و در نتیجه، داریم:
$$ \large \begin {align*} V & = 2 \pi \int _ 0 ^ 1 ( 3 - x ) ( 2 x ) \ d x \\[5pt] & = 2 \pi \int _ 0 ^ 1 \big ( 6 x - 2 x ^ 2 ) \ d x \\[5pt] & = 2 \pi \left ( 3 x ^ 2 - \dfrac 2 3 x ^ 3 \right ) \Big | _ 0 ^ 1 \\ [5pt] & = \dfrac { 1 4 } { 3 } \pi \approx 1 4 . 6 6 . \end {align*} $$
وقتی ناحیه حول یک محور افقی میچرخد، باید دقت کنیم که توابع شعاع و ارتفاع را برحسب $$ y $$ بنویسیم، نه $$ x $$.
مثال ۹
حجم حاصل از دوران ناحیه مثال قبل را حول محور $$ x $$ بیابید.
حل: ناحیه در شکل ۷ (الف) با یک عنصر دیفرانسیلی نمونه رسم شده است. در بخش (ب) شکل پوسته با عنصر دیفرانسیلی رسم شده تشکیل شده و جسم در شکل (ج) نشان داده شده است.
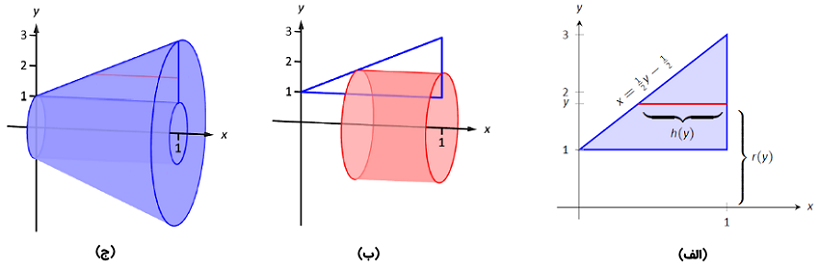
ارتفاع عنصر دیفرانسیلی فاصله در جهت $$ x $$ بین $$x=\dfrac12y-\dfrac12 $$ و $$ x = 1 $$ است. بنابراین، $$h(y) = 1-(\dfrac12y-\dfrac12) = -\dfrac12y+\dfrac32 $$. شعاع فاصله $$ y $$ از محور $$ x $$ است، بنابراین، $$ r ( y ) = y $$. محدودههای $$ y$$ ناحیه $$ y = 1 $$ و $$ y = 3 $$ است و منجر به انتگرال زیر میشود:
$$ \large \begin {align*} V & = 2 \pi \int _ 1 ^ 3 \left [ y \left ( - \dfrac 1 2 y + \dfrac 3 2 \right ) \right ] \ d y \\[5pt] & = 2 \pi \int _ 1 ^ 3 \left [ - \dfrac 1 2 y ^ 2 + \dfrac 3 2 y \right ] \ d y \\[5pt] & = 2 \pi \left [ - \dfrac 1 6y ^ 3 + \dfrac 3 4 y ^ 2 \right ] \Big | _ 1 ^ 3 \\[5pt] & = 2 \pi \left [ \dfrac 9 4 -\dfrac 7 { 1 2 } \right ] \\[5pt] & = \dfrac { 1 0 } { 3 } \pi \approx 1 0 . 4 7 2 . \end {align*} $$
مثال ۱۰
حجم جسمی را پیدا کنید که حاصل از دوران ناحیه محدود به $$ y = \sin x $$ و محور $$ x $$ از $$ x = 0 $$ تا $$ x = \pi $$ حول محور $$ y $$ است.
حل: ناحیه و عنصر دیفرانسیلی، پوسته تشکیل شده از عنصر دیفرانسیلی، و جسم حاصل در شکل زیر نشان داده شده است.
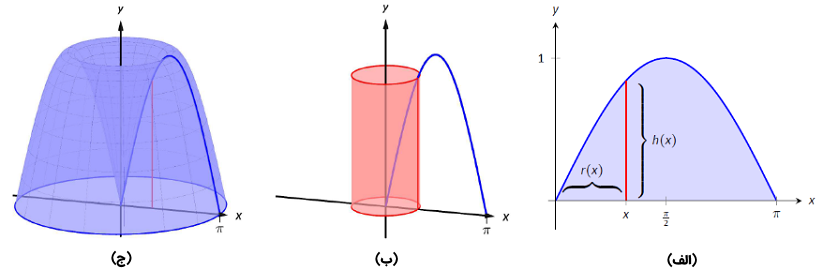
شعاع یک پوسته نمونه $$ r ( x ) = x $$ است. ارتفاع یک پوسته نمونه $$ h ( x ) = \sin x $$ از $$ x = 0 $$ تا $$ x = \pi $$ است. بنابراین، حجم جسم برابر است با:
$$ \large V = 2 \pi \int _ 0 ^ { \pi } x \sin x \ d x . $$
از انتگرالگیری جزء به جزء کمک میگیریم و با قرار دادن $$ u = x $$ و $$ d v = \sin x d x $$، خواهیم داشت:
$$ \large \begin {align*} V& = 2 \pi \Big [ - x \cos x \Big | _ 0 ^ { \pi } + \int _ 0 ^ { \pi } \cos x \ d x \Big ] \\[5pt]
& = 2 \pi \Big [ \pi + \sin x \Big | _ 0 ^ { \pi } \ \Big ] \\[5pt] & = 2 \pi \Big [ \pi + 0 \Big ] \\[5pt]
& = 2 \pi ^ 2 \approx 1 9 . 7 4 . \end {align*} $$
اگر مطلب بالای برای شما مفید بوده است و به یادگیری مباحث مشابه آن علاقهمند هستید، آموزشهای زیر نیز به شما پیشنهاد میشوند:










