کنترل پیش بین مدل (MPC) – راهنمای جامع

کنترل پیش بین مدل (Model Predictive Control)، یک کنترل‌کننده پیشرفته برای کنترل فرآیندهای صنعتی است که در آن می‌توان قیدهای فیزیکی حاکم بر سیستم را در هنگام طراحی در نظر گرفت. مزیت دیگر کنترل ‌پیش‌بین مدل این است که این کنترل‌کننده در واقع همان کنترل بهینه است، اما به صورت بلادرنگ (Real-time) و آنلاین بهینه‌سازی آن انجام می‌شود. در این آموزش قصد داریم به مبانی این کنترل‌کننده مهم بپردازیم و مزایا و معایب آن را بررسی کنیم.

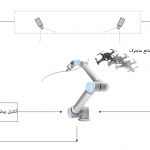
مقایسه کنترل تناسبی-انتگرالی-مشتقی (PID) و کنترل پیش بین مدل

در کنترل ‌پیش بین مدل سیگنال کنترلی همواره از طریق حل یک مسئله بهینه‌سازی مقید حاصل می‌شود. تابع هزینه مسئله بهینه‌سازی، بسته به نوع پلانت می‌تواند انرژی مصرفی، سوخت مصرفی، انرژی خطای ردیابی و... باشد. برای درک بهتر عملکرد کنترل‌ پیش بین مدل بهتر است که مقایسه‌ای بین کنترل‌کننده رایج تناسبی-انتگرالی-مشتقی PID و کنترل‌ پیش‌بین مدل به منظور کنترل سرعت یک موتور جریان مستقیم 12 ولت داشته باشیم.

فیلم آموزش کنترل پیش بین مدل با متلب در فرادرس

کلیک کنید

در هنگام طراحی پارامترهای کنترل‌کننده PI ما فقط مشخصه‌های حوزه فرکانس یا زمان (مانند درصد بالازدگی، زمان نشست، پهنای باند و...) را در نظر می‌گیریم و کاری به انرژی مصرفی سیستم کنترل نداریم. اما به دلیل این‌که موتور 12 ولت است، نباید ولتاژی بیشتر از آن را به موتور اعمال کنیم، چون ممکن است موتور بسوزد. پس سیگنال کنترلی باید کوچکتر از 12 ولت باشد که این قید را نمی‌توان در تنظیم پارامترهای کنترل‌کننده PI در نظر گرفت. از طرف دیگر، مسائل انرژی مصرفی و قیدهای مربوط به سیگنال‌های کنترلی و حتی خود حالت‌های سیستم را می‌توان در کنترل‌ پیش‌بین مدل در نظر گرفت. برای مثال می‌توان کنترل‌کننده‌ای طراحی کرد که سیگنال کنترلی کمتر از 12 ولت باشد، سرعت موتور هیچ وقت بزرگتر از 1000 دور بر دقیقه نشود و همزمان با برآورده شدن این قیدها انرژی مصرفی موتور نیز حداقل شود.

اصول کنترل‌ پیش بین مدل (MPC)

کنترل پیش‌بین مدل بر اساس بهینه‌سازی تکراری (آنلاین) یک تابع هزینه با افق محدود از عملکرد پلانت کار می‌کند. شکل زیر اصول کار این کنترل‌کننده محبوب را نشان می‌دهد. فرض کنید که وضعیت تمام سیگنال‌های موجود در سیستم تا نمونه kام در دسترس باشد، یعنی حالت‌ها و خروجی‌های سیستم از نمونه 0 تا نمونه kام و همچنین سیگنال کنترلی نیز از نمونه $$0$$ تا $$k-1$$ ام در دسترس باشند. دقت کنید که اگر زمان نمونه‌بردای مشخص باشد، شماره نمونه به راحتی تبدیل به زمان واقعی خواهد شد ($$t = kT_s$$). به همین دلیل از این به بعد به جای نمونه از زمان استفاده می‌کنیم تا درک مطلب واضح‌تر شود. حال هدف این است که سیگنال‌های کنترلی از زمان k تا زمان $$k+p‌$$ را طوری تعیین کنیم، که خروجی سیستم از زمان $$k$$ تا زمان $$k+p$$ تا حد ممکن به خروجی مرجع نزدیک باشد.

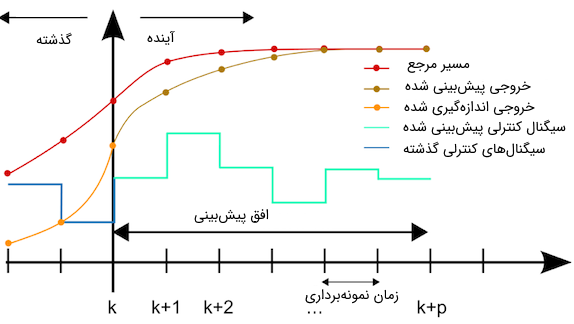
برای این کار باید خروجی سیستم از زمان $$k$$ تا زمان $$k+p$$ پیش‌بینی شود، که با توجه به مشخص بودن مدل دینامیکی سیستم، به راحتی می‌توان پیش‌بینی را انجام داد. به پارامتر $$p$$ افق پیش‌بینی گفته می‌شود و در واقع طول بازه پیش‌بینی را نشان می‌دهد. اگر فرض کنیم که مدل دینامیکی گسسته سیستم به صورت زیر باشد:

$$y(k+1)=y(k)+0.5u(k)$$

آنگاه با توجه به اینکه اطلاعات خروجی سیستم تا زمان $$k$$ و اطلاعات سیگنال کنترلی تا زمان $$k-1$$ مشخص است، پس خروجی یک نمونه به جلو یا یک گام به جلو بصورت زیر خواهد بود:

$$\widehat{y}(k+1\mid k)=y(k)+0.5 u(k)$$

از علامت $$\widehat{y}$$ ‌برای نشان دادن مقادیر پیش‌بینی استفاده می‌شود و $$\widehat{y}(k+1\mid k)$$ به معنی پیش‌بینی یک گام به جلو با داشتن اطلاعات تا زمان k است. حال با جایگذاری $$k+1$$ به جای $$k$$ در رابطه بالا پیش‌بینی دو گام به جلو به دست می‌آید:

$$\widehat{y}(k+2\mid k)=y(k)+0.5u(k)+0.5 u(k+1)$$

به همین ترتیب، با جایگذاری‌های متوالی، پیش‌بینی تا $$p$$ گام به جلو انجام می‌شود.

$$\widehat{y}(k+p\mid k)=y(k)+0.5u(k)+0.5 u(k+1)+...0.5u(k+p-1)$$

واضح است که تمام پیش‌بینی‌ها، وابسته به سیگنال کنترلی در طول افق پیش‌بین (یعنی $$u(k)$$ تا $$u(k+p-1)$$) هستند. حال برای اینکه پیش‌بینی‌ها تا حد امکان به خروجی‌های مرجع نزدیک باشند، اغلب از تابع هزینه مجموع مربعات خطای ردیابی استفاده می‌شود. خطای ردیابی $$n$$ گام به جلو به صورت زیر تعریف می‌شود:

$$e(k+n)=y_{ref}(k+n)-\widehat{y}(k+n)$$

که در آن $$n$$ می‌توان از یک تا $$p$$ تغییر کند و $$y_{ref}(k+n)$$ مقدار سیگنال مرجع می‌باشد. حال مجموع مربعات خطا به صورت زیر تعریف می‌شود:

$$Cost=\sum_{i=1}^{i=p} (y_{ref}(k+n)-\widehat{y}(k+n))^{2}$$

با بهینه‌سازی تابع هزینه بالا، سیگنال کنترلی در طول افق پیش‌بین به دست می‌آید. اما همان‌طور که قبلا اشاره شد، علاوه بر حداقل‌سازی تابع هزینه باید قیدهای فیزیکی نیز برآورده شوند. بهینه‌سازی تابع هزینه بالا ممکن است منجر به سیگنال کنترلی با دامنه بالا شود. برای رفع این مشکل، انرژی سیگنال کنترلی در طول افق پیش‌بین نیز به تابع هزینه اضافه می‌شود:

$$Cost=\sum_{i=1}^{i=p} (y_{ref}(k+n)-\widehat{y}(k+n))^{2}+ \rho\sum_{i=1}^{i=p-1}u(k+i)^{2}$$

جمله دوم در تابع هزینه، باعث می‌شود که مصالحه‌ای بین دامنه سیگنال کنترلی و خطای ردیابی برقرار شود. پارامتر $$\rho$$ به منظور تنظیم اهمیت نسبی خطای ردیابی نسبت به دامنه سیگنال کنترلی استفاده می‌شود. هرچه خطای ردیابی نسبت به دامنه سیگنال کنترلی اهمیت بیشتری داشته باشد، اندازه $$\rho$$ کوچکتر انتخاب می‌شود.

مسئله بهینه‌سازی بالا نامقید است و اگر بخواهیم قید سیگنال کنترلی صد در صد رعایت شود، باید مسئله بهینه‌سازی مقید زیر را محاسبه کنیم:

$$u(k)=\min_{SubjectTo \;\; u(t+k)\in [u_{min}\;u_{max}]}Cost=\sum_{i=1}^{i=p} (y_{ref}(k+n)-\widehat{y}(k+n))^{2}+ \rho\sum_{i=1}^{i=p-1}u(k+i)^{2}$$

حال اگر خروجی‌های پیش‌بینی شده نیز مقید باشند (مثلا سرعت موتور هیچ وقت بزرگتر از 1000 دور بر دقیقه نشود)، مسئله بهینه‌سازی به صورت زیر تغییر پیدا می‌کند:

$$u(k)=\min_{SubjectTo \;\;\begin{cases} u(t+k)\in [u_{min}\;u_{max}]\\ y(t+k)\in [y_{min}\;y_{max}] & \end{cases} }Cost=\sum_{i=1}^{i=p} (y_{ref}(k+n)-\widehat{y}(k+n))^{2}+ \rho\sum_{i=1}^{i=p-1}u(k+i)^{2}$$

اصل افق کاهنده (Receding Horizon Principle)

دقت کنید که تابع هزینه تعریف شده دارای متغیرهای $$u(k)$$ تا $$u(k+p-1)$$ است و با حل مسئله بهینه‌سازی مقادیر بهینه آن‌ها محاسبه می‌شوند. اما طبق اصل افق کاهنده فقط اولین مقدار محاسبه شده مربوط به سیگنال کنترلی بهینه به پلانت اعمال می‌شود و در زمان بعدی یعنی $$k+1$$، تمام محاسبات قبل دوباره تکرار خواهد شد. پس فقط $$(k)u$$ به پلانت اعمال می‌شود و اثر آن یعنی $$y(k+1)$$ اندازه‌گیری می‌شود. حال ما اطلاعات خروجی سیستم تا زمان $$k+1$$ را داریم و دوباره با طی کردن مسیر قبل، سیگنال کنترلی بهینه جدید $$u(k+1)$$ را به دست می‌آوریم و آن را به پلانت اعمال می‌کنیم تا $$y(k+2)$$ به دست آید و همین فرآیند را همواره تکرار می‌کنیم.

دلیل استفاده از اصل افق کاهنده، کاهش اثر عدم قطعیت‌ها، اغتشاشات و نویزهای موجود در سیستم است. زیرا این سیگنال‌ها اغلب دارای ماهیت تصادفی هستند و تا زمانی‌ که رخ ندهند، نمی‌توانیم آن‌ها را اندازه‌گیری کنیم. حال اگر کل سیگنال کنترلی یعنی $$u(k)$$ تا $$u(k+p-1)$$ به پلانت اعمال شود، بدین معنی است که اثرات اغتشاشات در طول افق پیش‌بین لحاظ نخواهد شد. اما با $$p$$ بار تکرار مسئله بهینه‌سازی و اندازه‌گیری اثرات اغتشاشات در هر نمونه‌برداری می‌توان اثرات آن‌ها را نیز جبران کرد.

افق کنترل

در توضیحات قبل اشاره شد که هدف تعیین سیگنال کنترلی در طول افق پیش‌بین برای حداقل‌سازی تابع هزینه و با در نظر گرفتن قیدهای حاکم بر سیستم است. در واقع در این حالت، افق کنترل برابر افق پیش‌بین در نظر گرفته شده است. افق کنترل طول بازه‌ای از سیگنال کنترلی را مشخص می‌کند که با استفاده از آن می‌خواهیم تابع هزینه را حداقل‌سازی کنیم. اما اغلب افق کنترل را کمتر از افق پیش‌بین در نظر می‌گیرند. به عبارت دیگر، هدف این است که با سیگنال‌های کنترلی $$u(k)$$ تا $$u(k+q-1)$$، خروجی‌های پیش‌بینی شده سیستم یعنی $$y(k+1)$$ تا $$y(k+p)$$ تا حد امکان به مقادیر مرجع آن‌ها نزدیک باشند. در این شرایط، به پارامتر $$q$$ افق کنترلی گفته می‌شود و کوچکتر از افق پیش‌بین است ($$q$$).

مزایای کنترل پیش‌بین مدل

همان‌طور که قبلا اشاره کردیم، مزیت برجسته کنترل‌ پیش‌بین مدل، بهینه‌سازی آنلاین همراه با در نظر گرفتن قیدهای فیزیکی حاکم بر سیستم است. اما این تنها خاصیت کنترل پیش‌بین مدل نیست.

فیلم آموزش طراحی کنترل پیش بین مبتنی بر مدل MPC در متلب MATLAB در فرادرس

کلیک کنید

سایر نقاط قوت کنترل پیش‌بین مدل عبارتند از:

• ذخیره‌سازی انرژی و هزینه: با درنظر گرفتن انرژی سیگنال کنترلی در تابع هزینه می‌توان مصرف انرژی سیستم را کاهش داد که به نوبه خود باعث کاهش هزینه‌های سیستم خواهد شد.
• جبران موثر اغتشاشات وارد بر سیستم: با استفاده از اصل افق کاهنده اثرات اغتشاشات (عدم قطعیت‌ها و نویزها) در کنترل پیش‌بین مدل نسبت به سایر کنترل‌کننده‌ها به صورت موثرتری حذف خواهد شد.
• کنترل سیستم‌های چند متغیره: تعمیم کنترل پیش‌بین مدل به سیستم‌های چند متغیره بسیار سرراست و مستقیم است و باعث پیچیدگی زیادی نمی‌شود. در حالی که طراحی کنترل‌کننده‌های کلاسیک مانند PID برای سیستم‌های چند متغیره بسیار سخت‌تر و چالش‌برانگیزتر از سیستم‌های تک‌متغیره است.
• پیاده‌سازی آسان در سیستم‌های دیجیتال:‌ بر خلاف تئوری‌های پیچیده کنترل بهینه که نیازمند حل معادلات دیفرانسیل غیرخطی و پیچیده هستند، کنترل پیش‌بین مدل به راحتی در کامپیوترهای دیجیتال قابل پیاده‌سازی است.
• کاربرد در صنعت: کنترل‌کننده پیش‌بین مدل از صنعت نشات گرفته است و بسیاری از استراتژی‌های کنترل پیش‌بین مدل به خوبی بر روی پلانت‌های صنعتی مانند ربات‌ها، توربین‌های بادی و بخار، اتوپایلوت، نورد فلزات، تولید سیمان و صنایع نفت و پتروشیمی کارایی خودشان را نشان داده‌اند.

معایب کنترل پیش‌بین مدل

بزرگترین عیب کنترل‌ پیش بین مدل، نیاز آن به مدل دقیق فرآیند است، زیرا در این کنترل‌کننده در قدم اول باید رفتار آینده سیستم پیش‌بینی شود. بنابراین اگر مدل ریاضی سیستم دقیق نباشد، پیش‌بینی‌های خروجی سیستم نیز معتبر نخواهد بود و در نتیجه منجر به خطا خواهد شد.

فیلم آموزش تنظیم پارامترهای کنترل پیش بین مدل (رایگان) در فرادرس

کلیک کنید

پیچیده‌ شدن حل مسئله بهینه‌سازی برای سیستم‌های غیرخطی عیب دیگر کنترل‌پیش بین است. اگر دینامیک سیستم غیرخطی باشد آنگاه تابع هزینه کنترل پیش‌بین مدل یک تابع پیچیده از متغیرهای تصمیم (سیگنال کنترلی در طول افق کنترل) خواهد شد و بهینه‌سازی آن مشکلات زیادی را به همراه خواهد شد. البته برای رفع این مشکل می‌توان با تعریف یک تبدیل (نگاشت) غیرخطی، سیستم غیرخطی را به یک سیستم خطی تبدیل کرد. دقیقا همانند کاری که در تئوری کنترل غیرخطی در روش فیدبک خطی‌ساز انجام می‌شود.

الگوریتم‌های حل مسئله بهینه‌سازی

اگر کنترل پیش‌بین مدل نامقید باشد، می‌توان به صورت تحلیلی مسئله بهینه‌سازی را حل کرد. کافی است که از تابع هزینه نسبت به متغیرهای تصمیم مشتق گرفته و ریشه مشتق را محاسبه کرد. اما اگر تابع هزینه کنترل پیش‌بین مدل مقید باشد، اغلب از روش‌های تکراری برای بهینه‌سازی آن استفاده می‌کنند. معروف‌ترین الگوریتم‌های بهینه‌سازی تکراری Interior-point ،SQP‌ و Active-Set هستند که در نرم‌افزار مهندسی متلب (MATLAB) در دستور fmincon گنجانده شده است.

نرم‌افزارهای تجاری نیز برای بهینه‌سازی تابع هزینه، هنگام پیاده‌سازی صنعتی کنترل‌ پیش‌بین مدل وجود دارند که یکی از مهم‌ترین آنها تولباکس yalmip است که با استفاده از این نرم‌افزار بسیاری از مسائل بهینه‌سازی نامقید، مقید، خطی و غیرخطی قابل حل است.

انواع استراتژی‌های کنترل پیش‌بین مدل

استراتژی‌های مختلفی برای کنترل پیش‌بین مدل ذکر شده‌اند که در همه آنها از سه اصل زیر استفاده می‌شود:

• استفاده صریح از مدل دینامیکی فرآیند به منظور پیش‌بینی رفتار آینده سیستم
• محاسبه سیگنال کنترلی بهینه با بهینه‌سازی تابع هزینه و در نظر گرفتن قیود آن
• اصل افق کاهنده

اما تفاوت آنها در موارد زیر است:

• نوع مدل فرآیند برای پیش‌بینی:‌ برخی از الگوریتم‌ها از پاسخ پله سیستم، برخی دیگر از مدل تابع تبدیل و برخی دیگر از مدل فضای حالت سیستم برای پیش‌بینی استفاده می‌کنند.
• شیوه در نظر گرفتن اغتشاشات وارد بر سیستم.
• نوع تابع هزینه: اغلب از مجموع مربعات خطای ردیابی و سیگنال کنترلی به عنوان تابع هزینه استفاده می‌شود. اما می‌توان مجموع قدرمطلق‌های خطای ردیابی و سیگنال کنترلی و یا هر تابع هزینه‌ای دیگری را بسته به نوع پلانت در نظر گرفت.

با توجه به این تفاوت‌ها، مهمترین استراتژی‌های کنترل پیش‌بین مدل عبارتند از:

• الگوریتم MAC: استفاده از پاسخ ضربه تجربی سیستم برای پیش‌بینی سیستم.
• الگوریتم DMC: استفاده از پاسخ پله تجربی سیستم برای پیش‌بینی سیستم.
• الگوریتم PFC:‌ استفاده از مدل‌سازی فضای حالت سیستم برای پیش‌بینی سیستم.
• الگوریتم GPC:‌ استفاده از مدل‌سازی تابع تبدیل گسسته سیستم برای پیش‌بینی سیستم.
• الگوریتم کنترل پیش‌بین مدل غیرخطی NMPC:‌ کنترل پیش‌بین مدل برای سیستم‌های غیرخطی.

در مقالات بعدی، درباره هر کدام از این الگوریتم‌ها توضیح داده خواهد شد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های مهندسی کنترل
• آموزش کنترل پیش بین مدل با متلب (لینک آموزش)
• مجموعه آموزش مهندسی برق
• مجموعه آموزش های برنامه نویسی متلب (MATLAB)
• سیستم LTI — از صفر تا صد
• سیستم کنترل حلقه باز — به زبان ساده
• فیدبک (Feedback) در سیستم های کنترل — مفاهیم اصلی

^^