نامساوی مارکف و اثبات آن – از صفر تا صد

نامساوی‌هایی که برمبنای احتمال و برای متغیرهای تصادفی مورد استفاده قرار می‌گیرند، نقشی مهم در آمار و استنباط آماری ایفا می‌کنند. به کمک این نامساوی‌ها قادر هستیم برای مقادیر احتمالاتی، کران‌‌هایی در نظر بگیریم. در این نوشتار به بررسی یک نامساوی مهم به نام نامساوی مارکف خواهیم پرداخت که در آمار و بخصوص آمار ریاضی، نقش مهمی در اثبات قضیه‌های دیگر دارد.

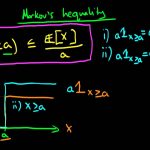
از آنجایی که در بیشتر نامساوی‌ها، تابع احتمال و فاصله متغیر تصادفی از میانگین آن مورد بررسی قرار می‌گیرد، مطالعه نوشتارهای امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال توصیه می‌شود. همچنین خواندن نامساوی چبیشف – کاربرد در توزیع‌های غیرنرمال و نامساوی چبیشف و اثبات آن --- از صفر تا صد نیز خالی از لطف نیست.

نامساوی مارکف و اثبات آن

براساس نامساوی مارکف، می‌توان یک کران بالا برای مقدار احتمال پیشامدی پیدا کرد که در آن یک متغیر تصادفی نامنفی از مقدار ثابت و مشخصی (مثل $$a$$) بزرگتر باشد.

این نامساوی اولین بار توسط ریاضی‌دان روسی «آندری مارکف» (Andry Markov) براساس کارهایی که استادش «پافناتی چبیشف» (Pafnuty Lvovich Chebyshev) انجام داده بود، معرفی و به افتخار او نامساوی مارکف نامیده شد. البته گاهی به نامساوی مارکف، نامساوی اول چبیشف یا نامساوی بینایم (Bienaymé) نیز می‌گویند زیرا هر دو، بطور جداگانه در بررسی این نامساوی نقش داشته‌اند.

این نامساوی مرتبط با احتمال و امید ریاضی متغیر تصادفی است و یک کران برای تابع احتمال توزیع تجمعی متغیر تصادفی X در شرایط خاص ایجاد می‌کند.

نامساوی مارکف

بیان رسمی نامساوی مارکف در ادامه مورد بررسی قرار می‌گیرد. فرض کنید متغیر تصادفی $$X$$ دارای تکیه‌گاهی با مقادیر نامنفی است. بنابراین اگر $$S_X$$ را تکیه‌گاه $$X$$ بنامیم، داریم:

$$\large S_x = [0,\infty)$$

به این ترتیب اگر $$E(X)$$، امید ریاضی (Mathematical Expectation) یا مقدار چشم‌داشتی (Expected Value) برای متغیر تصادفی $$X$$ باشد، برای هر مقدار مثبتی مثل $$a$$ خواهیم داشت:

$$\large {\displaystyle \operatorname {P} (X\geq a)\leq {\frac {\operatorname {E} (X)}{a}}}$$

رابطه ۱

در نتیجه نسبت امید ریاضی به مقدار $$a$$، تشکیل یک کران برای مقدار احتمال یا تابع توزیع تجمعی متغیر تصادفی $$X$$ خواهد داد.

می‌توان نامساوی مارکف را به شکل دیگری نیز نشان داد. فرض کنید $${\displaystyle a={\tilde {a}}\cdot \operatorname {E} (X)}$$. واضح است که در این حالت هم $$\tilde{a}>0$$ زیرا هم $$X$$ و هم $$a$$ نامنفی هستند. آنگاه نامساوی مارکف به صورت زیر نوشته خواهد شد.

$$\large {\displaystyle \operatorname {P} (X\geq {\tilde {a}}\cdot \operatorname {E} (X))\leq {\frac {1}{\tilde {a}}}}$$

به این ترتیب یک کران بالا برای احتمال پیشامدی پیدا می‌شود که در آن متغیر تصادفی $$X$$‌ از مضارب امید ریاضی خودش بزرگتر باشد.

نامساوی مارکف در نظریه اندازه

نامساوی مارکف در نظریه اندازه (Measure Theory) نیز به کار می‌رود. فرض کنید که سه تایی $$(X,\Sigma , \mu)$$ یک فضای اندازه (Measure Space) باشند. واضح است که $$X$$ یک مجموعه $$\mu$$‌-اندازه‌پذیر و $$\Sigma$$ نیز میدان سیگمایی آن است. $$\mu$$ نیز یک اندازه تعریف شده روی $$\Sigma$$ است.

اگر $$f$$ یک تابع حقیقی-مقدار و $$\mu$$-اندازه‌پذیر ($$\mu \;-measurable$$) باشد، برای هر $$\varepsilon>0$$، می‌توان نوشت:

$$\large {\displaystyle \mu (\{x\in X:|f(x)|\geq \varepsilon \})\leq {\frac {1}{\varepsilon }}\int _{X}|f|\,d\mu }$$

نکته: گاهی به این نامساوی که براساس اندازه $$\mu$$ نوشته شده، نامساوی چبیشف می‌گویند.

نامساوی مارکف تعمیم یافته برای توابع یکنوا صعودی

نامساوی مارکف، برای توابع یکنوایی از متغیر تصادفی نیز، به کار گرفته می‌شود. در این حالت به آن نامساوی مارکف تعمیم یافته می‌گویند.

فرض کنید تابع $$\varphi$$ تابعی یکنوا و صعودی با مقادیر نامنفی است. دراین صورت برای $$a>0$$ و $$\varphi(a)>0$$ و متغیر تصادفی $$X$$ (نه لزوما نامنفی) داریم:

$$\large{\displaystyle \operatorname {P} (|X|\geq a)\leq {\frac {\operatorname {E} (\varphi (|X|))}{\varphi (a)}}}$$

نکته: از آنجایی که تابع $$X^n$$ تابع صعودی و یکنوا روی مقادیر مثبت $$X$$ است، می‌توانیم نامساوی مارکف را برای گشتاورهای متغیر تصادفی $$X$$ نیز به کار ببریم. به شرطی که محاسبات نامساوی مارکف روی مقادیر مثبت از تکیه‌گاه متغیر تصادفی $$X$$ صورت گیرد.

$$\large{\displaystyle \operatorname {P} (X\geq a)\leq {\frac {\operatorname {E} (|X|^{n})}{a^{n}}}}$$

در اینجا هم $$a$$ مقداری نامنفی است.

اثبات نامساوی مارکف

اثبات نامساوی مارکف را ابتدا برای فضای احتمال مورد بررسی قرار می‌دهیم زیرا در این حوزه کاربرد بیشتری دارد. سپس به اثبات آن در فضای اندازه می‌پردازیم.

فیلم آموزش آمار و احتمالات مهندسی – حل نمونه سوالات کنکور ارشد در فرادرس

کلیک کنید

نامساوی مارکف و اثبات آن در فضای احتمال

اثبات نامساوی مارکف در فضای احتمال را به دو شیوه می‌توان انجام داد. در روش اول، با توجه به تعریف امید ریاضی برای متغیر تصادفی $$X$$ عمل می‌شود. ولی در شیوه دوم، براساس تابع نشانگر روی متغیر تصادفی $$X$$، نامساوی مارکف را اثبات می‌کنند.

روش اول: با استفاده از امید ریاضی متغیر تصادفی $$X$$

همانطور که می‌دانید با توجه به تعریف امید ریاضی می‌توان نوشت:

$$\large {\displaystyle \operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,dx}$$

حال اگر متغیر تصادفی $$X$$ دارای تکیه‌گاه اعداد حقیقی نامنفی باشد می‌نویسیم:

$$\large {\displaystyle \operatorname {E} (X)=\int _{-\infty }^{\infty }xf(x)\,dx=\int _{0}^{\infty }xf(x)\,dx}$$

به این ترتیب با افراز ناحیه $$[0,\infty)$$ به نواحی صفر تا $$a$$ و از $$a$$ تا بی‌نهایت می‌توانیم رابطه بالا را به صورت زیر بنویسیم. دقت داشته باشید که $$a>0$$‌ است.

$$\large {\displaystyle \operatorname {E} (X)=\int _{0}^{a}xf(x)\,dx+\int _{a}^{\infty }xf(x)\,dx}$$

با حذف عبارت اول (که مشخص است مقداری مثبت است)، نامساوی زیر حاصل می‌شود.

$$\large E(X) \geq \int _{a}^{\infty }xf(x)\,dx\geq \int _{a}^{\infty }af(x)\,dx=a\int _{a}^{\infty }f(x)\,dx$$

از آنجایی که کران پایین برای ناحیه انتگرال، مقدار $$a$$‌ است نامساوی بالا شکل گرفته است.

$$\large E(X) \geq a\;\operatorname {Pr} (X\geq a)$$

توجه داشته باشید که نامساوی آخر با توجه به رابطه $$a$$ بدست می‌آید. به این ترتیب با تقسیم رابطه بالا بر $$a$$، نامساوی مارکف اثبات می‌شود.

$$\large {\displaystyle \Pr(X\geq a)\leq \dfrac{\operatorname {E} (X)}{a}}$$

روش دوم: با استفاده از امید ریاضی تابع نشانگر

فرض کنید تابع نشانگر برای هر پیشامد در فضای احتمال به صورت $$I_E$$ نشان داده شود. در این صورت نحوه محاسبه تابع نشانگر را به صورت زیر تعریف می‌کنیم:

$$\large I_E= \begin{cases}1 &, P(E)=1\\0 &, P(E)=0\end{cases}$$

با توجه به این موضوع برای پیشامد $$X>a$$ از این تابع نشانگر استفاده می‌کنیم. پس براساس رابطه بالا خواهیم داشت:

$$\large I_{X\geq a}= \begin{cases}1 &, P(X\geq a)=1\\0 &, P(X<a)=0\end{cases}$$

به این ترتیب نامساوی زیر برای مقدار $$a>0$$ و تابع نشانگر (متغیر تصادفی) $$I_{(X\geq a)}$$ برقرار است.

$$\large aI_{(X\geq a)}\leq X$$

رابطه ۳

به این ترتیب زمانی که $$X$$ باشد، $$I_{(X\geq a)}=0$$ و در نتیجه $$aI_{(X\geq a)}=0\geq X$$‌ است. همچنین زمانی که $$X\geq a$$ است، آنگاه $$I_{(X\geq a)}=1$$‌ و در نتیجه $$a\;I_{(X\geq a)}=1\leq X$$.

توجه داشته باشید که تابع احتمال با افزایش مقدار $$X$$ نیز افزایش می‌یابد در نتیجه می‌توان آن را به عنوان یک تابع صعودی یکنوا در نظر گرفت. با گرفتن امید ریاضی از دو طرف رابطه ۳ خواهیم داشت:

$$\large {\displaystyle \operatorname {E} (aI_{(X\geq a)})\leq \operatorname {E} (X)}$$

رابطه ۴

از طرفی با توجه به نحوه محاسبه امید ریاضی برای یک پیشامد (تابع نشانگر)، طرف چپ نامساوی بالا را بسط داده، و به صورت زیر می‌نویسیم:

$$\large {\displaystyle a\operatorname {E} (I_{(X\geq a)})=a[1\cdot \operatorname {P} (X\geq a)+0\cdot \operatorname {P} (X<a)]=a\operatorname {P} (X\geq a)}$$

رابطه ۵

پس با مقایسه رابطه ۴ و ۵ خواهیم داشت:

$$\large {\displaystyle a\operatorname {P} (X\geq a)\leq \operatorname {E} (X)}$$

چون می‌دانیم $$a>0$$ پس تقسیم دو طرف نامساوی بر $$a$$، جهت را تغییر نمی‌دهد. به این ترتیب نامساوی مارکف اثبات خواهد شد.

$$\large {\displaystyle \operatorname {P} (X\geq a)\leq \dfrac{\operatorname{E}(X)}{a}}$$

نامساوی مارکف و اثبات آن در فضای اندازه

فرض کنید که تابع نامنفی $$f$$ با مقادیر حقیقی، روی یک فضای اندازه $$\mu$$ تعریف شده است. تابع حقیقی‌-مقدار $$s$$ روی $$X$$ را به صورت زیر در نظر بگیرید.

$$\large s(x) =\begin{cases}\varepsilon, & \text{if }\;\; f(x) \;\;\geq \varepsilon \\0, & \text{if }\;\; f(x)\;\; < \varepsilon\end{cases}$$

در نتیجه خواهیم داشت:

$$\large {\displaystyle 0\leq s(x)\leq f(x)}$$

با توجه به تعریف انتگرال لبگ (Lebesque Integral) داریم:

$$\large \int_X f(x) \, d\mu \geq \int_X s(x) \, d \mu = \varepsilon \mu( \{ x\in X : \, f(x) \geq \varepsilon \} )$$

مشخص است که $$\varepsilon>0$$ پس تقسیم آن بر دو طرف نامساوی، جهت را تغییر نمی‌دهد و نامساوی مارکف بدست می‌آید.

$$\large\mu(\{x\in X : \, f(x) \geq \varepsilon \}) \leq {1\over \varepsilon }\int_X f \,d\mu$$

کاربردهای نامساوی مارکف

نامساوی مارکف در اثبات نامساوی‌های دیگر که بخصوص براساس احتمال ساخته می‌شوند، کاربرد دارد. برای مثال می‌توانیم نامساوی چبیشف را حالت خاصی از نامساوی مارکف در نظر بگیریم.

همچنین این نامساوی برای توابع یکنوا و صعودی از متغیر تصادفی نیز باعث ایجاد نامساوی‌هایی جدیدی خواهد شد. در ادامه به این دو موضوع خواهیم پرداخت.

نامساوی مارکف و چبیشف

حتما در دیگر نوشتارهای فرادرس با نامساوی چبیشف (Chebyshev's inequality) و خصوصیات آن، آشنا شده‌اید. در اینجا می‌خواهیم به ارتباط نامساوی مارکف و چبیشف بپردازیم.

هر چند مارکف، دانشجوی چبیشف بوده ولی نامساوی چبیشف از نامساوی مارکف نیز می‌تواند به دست آید. بنابراین نامساوی مارکف، کلی‌تر است.

همانطور که می‌دانید، نامساوی چبیشف برای متغیر تصادفی $$X$$ با امید ریاضی و واریانس $$E(X)$$ و $$V(X)$$ به شکل زیر نوشته می‌شود.

$$\large {\displaystyle \operatorname {P} (|X-\operatorname {E} (X)|\geq a)\leq {\frac {\operatorname {Var} (X)}{a^{2}}}}$$

توجه داشته باشید که $$a>0$$ است. ازطرفی می‌دانیم که واریانس متغیر تصادفی $$X$$ به صورت زیر محاسبه می‌شود.

$$\large \operatorname{Var}(X) = \operatorname{E}[(X - \operatorname{E}(X) )^2]$$

در نتیجه می‌توانیم در نامساوی مارکف با قرار دادن $$(X-E(X))^2$$ به جای $$X$$ نامساوی چبیشف را بدست آوریم. واضح است که $$(X-E(X))^2$$ نامنفی است. در نتیجه طبق نامساوی مارکف می‌توان نوشت:

$$\large {\displaystyle \operatorname {P} ((X-\operatorname {E} (X))^{2}\geq a^{2})\leq {\frac {\operatorname {Var} (X)}{a^{2}}}}$$

اگر از دو طرف نامساوی مربوط به احتمال در رابطه بالا، جذر بگیریم و از نامساوی مارکف استفاده کنیم، نامساوی چبیشف را اثبات کرده‌ایم.

$$\large {\displaystyle \operatorname {P} (|X-\operatorname {E} (X)|\geq a)= \operatorname {P} \left((X-\operatorname {E} (X))^{2}\geq a^{2}\right)}$$

در رابطه‌ زیر، منظور از MI، استفاده از نامساوی مارکف است.

$$\large \operatorname {P} \left((X-\operatorname {E} (X))^{2}\geq a^{2}\right){\overset {\underset {\mathrm {MI} }{}}{\leq }}\,\dfrac{\operatorname {E} [X-\operatorname {E} (X)]^{2}}{a^{2}}=\\ \large \dfrac {\operatorname {Var} (X)}{a^{2}}$$

به این ترتیب نامساوی چبیشف حاصل می‌شود.

نامساوی مارکف برای توابع یکنوا و صعودی

همانطور که در معرفی نامساوی مارکف خواندید، حالت تعمیم یافته این نامساوی برای توابع یکنوا نیز معرفی شد. به این ترتیب می‌توانیم برای تابع یکنوا و صعودی $$\varphi$$ از هر متغیر تصادفی بنویسیم.

$$\large {\displaystyle \operatorname {P} (|X|\geq a)=\operatorname {P} {\big (}\varphi (|X|)\geq \varphi (a){\big )}\;\;{\overset {\underset {\mathrm {MI} }{}}{\leq }}\;\;{\dfrac {\operatorname {E} (\varphi (|X|))}{\varphi (a)}}}$$

توجه دارید که در اینجا با استفاده از قدرمطلق، شرایط نامساوی مارکف را برای متغیر تصادفی $$|X|$$ ایجاد کرده‌ایم.

نامساوی مارکف برای چندک‌های توزیع

یکی از کاربردهایی که نامساوی مارکف تعمیم یافته برای توابع یکنوا و صعودی دارد، پیدا کردن کران بالا برای چندک‌ها است. فرض کنید $$Q_X(p)$$ چندک $$p$$ام متغیر تصادفی $$X$$ باشد.

اگر تکیه‌گاه متغیر تصادفی $$X$$، مجموعه اعداد حقیقی نامنفی باشد، می‌توانیم بنویسیم:

$$\large {\displaystyle Q_{X}(1-p)\leq {\frac {\operatorname {E} (X)}{p}}}$$

زیرا با توجه به مفهوم چندک‌ $$p$$‌ داریم:

$$\large {\displaystyle p\leq \operatorname {P} (X\geq Q_{X}(1-p))\;\;{\overset {\underset {\mathrm {MI} }{}}{\leq }}\;\;{\dfrac {\operatorname {E} (X)}{Q_{X}(1-p)}}}$$

از آنجایی که چندک‌ها و مقدار $$p$$ مثبت هستند، جابجا کردن آن‌ها در رابطه بالا، باعث تغییر جهت نامساوی نمی‌شود. پس رابطه نامساوی مارکف برای چندک‌ها حاصل می‌شود.

یادآوری می‌کنیم که نماد $$MI$$ در رابطه بالا، بیانگر استفاده از نامساوی مارکف است.

تحقیق نامساوی مارکف در توزیع دو جمله‌ای و نرمال

در ادامه به بررسی نامساوی مارکف برای توزیع گسسته دو جمله‌ای و پیوسته نرمال می‌پردازیم. همانطور که می‌دانید، باید برای هر دو حالت، ابتدا مقدار تابع بقا ($$P(X>a)$$ را محاسبه کنیم. همچنین با توجه به مقدار $$a$$ طرف راست نامساوی یعنی $$E(X)/a$$ را بدست آوریم. در انتها نیز این دو مقدار را بوسیله یک نمودار با یکدیگر مقایسه می‌کنیم. البته واضح است که نمودار ترسیم شده از منحنی تابع بقا همیشه در پایین نمودار حاصل از امید ریاضی قرار خواهد گرفت.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

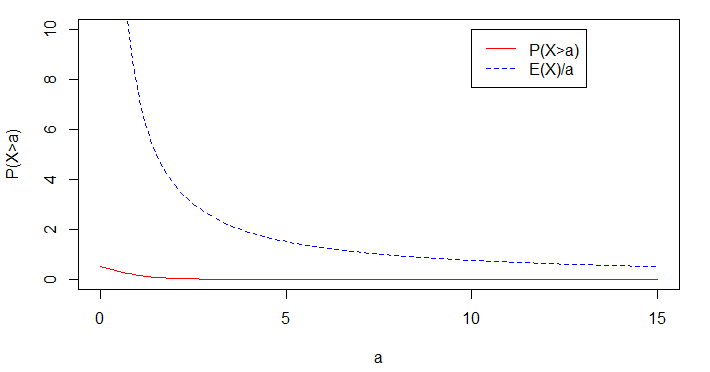
کد زیر که به زبان محاسباتی R نوشته شده است، به بررسی این نامساوی برای توزیع دو جمله‌ای با پارامترهای $$n=15$$‌ و $$p=0.5$$ پرداخته است. واضح است که مقدار $$a$$‌ از ۱ تا ۱۵ خواهد بود.

حاصل اجرای این برنامه نموداری به صورت زیر خواهد بود.

همانطور که مشاهده می‌کنید، فاصله این دو منحنی زمانی که مقدار $$a$$ به امید ریاضی متغیر تصادفی (در این حالت $$E(X)=np=10\times 0.5 = 5$$) نزدیک می‌شود، کمترین مقدار خود خواهد بود.

این بار براساس توزیع نرمال این نمودار را ترسیم می‌کنیم. البته توجه داریم که مقادیر $$X$$‌ در اینجا باید مثبت باشند. کد زیر به این منظور نوشته شده است.

نتیجه اجرای این برنامه، به شکل نموداری مطابق زیر خواهد بود.

خلاصه و جمع‌بندی

نامساوی مارکف یک نامساوی قوی است که برحسب احتمال و امید ریاضی متغیرتصادفی نوشته می‌شود. به کمک این نامساوی می‌توانیم برای تابع بقا $$P(X\geq a)$$ یا $$1-F(X)$$ یک کران بالا بدست آوریم. در این متن نامساوی مارکف و اثبات آن با شیوه‌های مختلف و فضاهای متفاوت مورد بحث قرار گرفت و به کاربردهای آن در اثبات نامساوی‌های دیگر نیز اشاره شد.

شاید در زندگی روزمره هم بتوان از نامساوی مارکف برای مقادیری که نامنفی هستند، استفاده کرد. برای مثال با فرض نامنفی بودن میزان درآمد به عنوان متغیر تصادفی، می‌توان از نامساوی مارکف نتیجه گرفت که احتمال اینکه فردی بیش از ۵ برابر میانگین درآمد جامعه را داشته باشد، کمتر از ۰٫۲ یا ۲۰٪ است. به این ترتیب می‌توان گفت که حداکثر ۲۰٪ مردم بیش از ۵ برابر میانگین درآمد جامعه، دریافتی دارند.

البته می‌دانیم که این رقم، بسیار کمتر از ۲۰٪ است ولی به هر حال بیشترین مقداری که می‌توان تصور کرد (کران بالا) برای چنین حالتی در اینجا ۲۰٪ است.

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های آمار و احتمالات
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^