معادلات و نامعادلات قدر مطلق – به زبان ساده
در آموزشهای قبلی مجله فرادرس، درباره قدر مطلق بحث شد. در این آموزش، معادلات و نامعادلات شامل قدر مطلق را با جزئیات بیشتری بررسی خواهیم کرد.


معادلات قدر مطلق
ابتدا تعاریف سادهای از قدر مطلق را بیان میکنیم: یک تعریف هندسی و یک تعریف ریاضی که هر دو در ادامه معرفی شدهاند.
تعریف هندسی
فرض کنید میخواهیم یک فاصله یا بازه را روی محوری بسنجیم که درجهبندی شده است. اگر کسی از ما بپرسد فاصله بین دو نقطه (که یک نقطه آن مبدا محور است) چقدر است، هیچگاه یک عدد منفی را به زبان نمیآوریم. اگر این گفته را کمی نظاممندتر کنیم، در تعریف هندسی، را فاصله از مبدا در نظر میگیریم. این معادل همان گفته است که همیشه یک عدد مثبت را بهعنوان فاصله در نظر میگیریم. شکل زیر را ببینید.
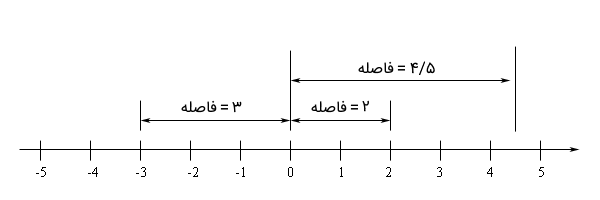
با توجه به شکل بالا، بدون در نظر گرفتن جهت و در بازه مثبت یا منفی بودن محور، مقادیر مطلق زیر را برای توصیف فاصله بیان میکنیم:
واضح است که فاصله مبدا از خودش برابر با صفر است، یعنی .
تعریف ریاضی
تعریف ریاضی قدر مطلق، بهصورت زیر است:
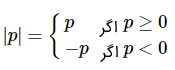
عبارت بالا به ما میگوید به عدد نگاه کنید؛ اگر بزرگتر یا مساوی با صفر بود، خودش را بنویسید و اگر منفی بود، علامت منفی آن را حذف کنید. مثالهای زیر، این موضوع را بهخوبی نشان میدهند:
بنابراین، قدر مطلق، هر عددی را مثبت میکند و این یعنی .
البته به شرایط تعریف قدر مطلق توجه کنید. برای مثال، عبارت را نمیتوان بهعنوان تعریف قدر مطلق نوشت، زیرا اطلاعی از مقدار نداریم.
همچنین باید توجه کنید که قدر مطلق به این معنا نیست که هر جا علامت منفی دیدیم، آن را به مثبت تبدیل کنیم. برای مثال:
حال چگونه یک معادله قدر مطلق را حل کنیم؟ اگر قدر مطلق را بهعنوان یک معادله داشته باشیم، چه میتوانیم بگوییم؟ با توجه به تعاریفی که بیان شد، اولین راهحلی که به ذهنمان میرسد، احتمالاً این جمله است: عدد حتماً یا بوده است که قدر مطلق آن برابر با است. این جمله ساده، اساس حل معادلات قدر مطلق است. فرمول کلی زیر، معادل ریاضی عبارتی است که بیان کردیم:

دقت کنید که باید یک عدد مثبت باشد. این عدد نمیتواند منفی باشد، چون حاصل قدر مطلق هیچ عددی منفی نیست. البته اگر صفر باشد، واضح است که نیز برابر با صفر است.
حال، چند مثال را درباره معادلات قدر مطلق بررسی میکنیم.
مثال ۱
معادله زیر را حل کنید:
حل: راه حل این معادله، چیزی جز فرمول اخیر نیست که بیان کردیم. کل عبارت داخل قدر مطلق را بهعنوان عدد در نظر میگیریم و بهسادگی مسئله را حل میکنیم. بنابراین، دو حالت داریم:
یا
از همین رو، دو معادله یک مجهولی ساده خواهیم داشت که باید آنها را حل کنیم.
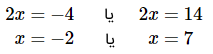
در نتیجه، به دو جواب و میرسیم.

مثال 2
معادله زیر را حل کنید:
حل: همانطور که قبلاً گفتیم، وقتی حاصل یک قدر مطلق صفر میشود، عبارت داخل آن نیز برابر با صفر است. بنابراین، میتوان مقدار مجهول را بهصورت زیر تعیین کرد:
مثال ۳
معادله زیر را حل کنید:
حل: چه عددی را به جای قرار دهیم که مقدار قدر مطلق برابر با شود؟ اولین چیزی که به ذهن میرسد، این است که قدر مطلق نمیتواند منفی باشد. پس هیچ حلی برای وجود ندارد.
مثال ۴
معادله زیر را حل کنید:
حل: همانطور که از قبل میدانیم، مقدار قدر مطلق، دو حالت دارد. بنابراین، داریم:
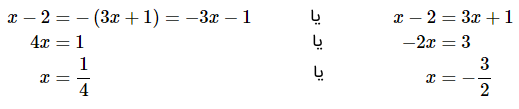
میبینیم که دو پاسخ بالقوه برای معادله وجود دارد. این دو پاسخ باید بهگونهای باشند که سمت راست معادله قدر مطلق منفی نشود. بعد از بهدست آمدن دو پاسخ، باید آنها را در معادله اصلی قرار داده و این موضوع را تحقیق کنیم. برای مشکلی وجود ندارد، اما برای داریم:
میبینیم که اندازه اعداد دو سمت با هم برابر است و علامت آنها با هم تفاوت دارد. با این تفاسیر، پاسخ معادله مورد سوال، است.
مثال ۵
معادله زیر را حل کنید:
حل: این مثال مانند مثال قبل است. بنابراین داریم:
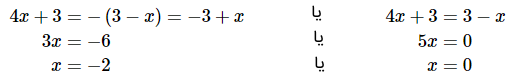
اگر دو پاسخ بهدست آمده را در معادله اصلی جایگذاری کنیم، میبینیم که هر دو پاسخ صحیح هستند. بنابراین، و ، پاسخ معادله فوق هستند.

مثال ۶
پاسخ معادله زیر را پیدا کنید:
حل: مشابه مثالهای قبل، داریم:

با توجه به اینکه در دو سمت معادله، قدر مطلق وجود دارد، نیازی نیست صحت پاسخهای بهدست آمده را بررسی کنیم. بنابراین، پاسخ معادله، و است.
نامعادلات قدر مطلق
در بخش قبل، معادلات قدر مطلق را بررسی کردیم. در این بخش، نامعادلاتی را معرفی خواهیم کرد که در آنها قدر مطلق وجود دارد. برای نامعادلهها دو حالت وجود دارد که آنها را به تفکیک بیان میکنیم.
نامعادلههای شامل و
مانند بخش معادلهها، از یک مثال بسیار ساده شروع میکنیم:
اگر از دیدگاه هندسی به مسئله بنگریم، نامعادله فوق بیان میکند فاصله از مبدا مهم نیست، مهم فقط این است که از بزرگتر نباشد. این یعنی در بازه زیر قرار گیرد:
مشابه عبارت بالا را برای علامت نیز داریم.
در حالت کلی، میتوانیم از فرمولهای زیر استفاده کنیم:

مانند معادلهها، در فرمول بالا باید مثبت باشد. در ادامه، چند مثال ارائه میکنیم.
مثال ۷
نامعادله زیر را حل کنید:
حل: طبق فرمولی که گفتیم، بهسادگی میتوان قدر مطلق را حذف کرد و نامعادله را بهصورت زیر نوشت:
با یک عملیات جبری بسیار ساده، به پاسخ نهایی خواهیم رسید:
بنابراین، پاسخ سوال، بازه است.
نامعادلههای شامل و
باز هم یک مثال ساده عددی را در نظر میگیریم:
عبارت بالا بیان میکند حداقل فاصله از مبدا باید باشد. به عبارت بهتر، یعنی:
یا
قبل از ارائه راهحل کلی مسئله، اشتباه رایجی را بیان میکنیم که معمولاً در بین دانشآموزان وجود دارد. بسیاری از دانشآموزان، دو نامعادله بالا را با هم ترکیب کرده و بهصورت زیر مینویسند:
عبارت بالا نادرست است. این عبارت میگوید عدد ، عددی است که بزرگتر یا مساوی و کوچکتر یا مساوی است. به نظرتان این عدد چیست؟ معلوم است که پاسخی برای آن وجود ندارد و از اساس غلط است.
هنگام برخورد با نامعادلههای شامل و ، از فرمولهای کلی زیر استفاده میکنیم:


مثال ۸
نامعادله زیر را حل کنید:
حل: نامعادله فوق را میتوان به دو نامعادله زیر تجزیه کرد:
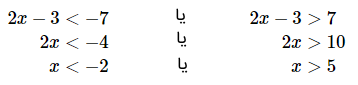
بنابراین، پاسخ نامعادله، یا است.
مثال ۹
نامعادله زیر را حل کنید:
حل: شاید در نگاه اول، برای حل این نامعادله دست به قلم شوید. اما، کمی بیشتر به آن دقت کنید. سوال میگوید که به ازای چه مقادیری از ، قدر مطلق باید بزرگتر یا مساوی با صفر باشد. چه وقت یک قدر مطلق، بزرگتر یا مساوی با صفر است؟ معلوم است، همیشه! به عبارت دیگر، به ازای همه ها، نامعادله فوق برقرار است. به بیان ریاضی، پاسخ نامعادله برابر است با .
آزمون معادلات و نامعادلات قدر مطلق
۱. کدام گزینه تعریف هندسی قدر مطلق یک عدد را بهدرستی بیان میکند؟
قدر مطلق فقط برای اعداد مثبت تعریف میشود.
قدر مطلق مقدار مثبت یا منفی هر عدد را نشان میدهد.
قدر مطلق مقدار عدد را دو برابر میکند.
قدر مطلق فاصله یک عدد تا عدد صفر روی محور عددها است.
عبارت «قدر مطلق فاصله یک عدد تا عدد صفر روی محور عددها است» تعریف هندسی درست را بیان میکند، زیرا در این رویکرد، مطلقا فاصله از مبداء مهم است، نه علامت عدد. گزینه «قدر مطلق مقدار مثبت یا منفی هر عدد را نشان میدهد» دقیق نیست، چون قدر مطلق فقط مقدار مثبت فاصله را نمایش میدهد. گزینه «فقط برای اعداد مثبت تعریف میشود» غلط است چون صفر و اعداد منفی هم قدر مطلق دارند. همچنین عبارت «قدر مطلق مقدار عدد را دو برابر میکند» درست نیست و ویژگی قدر مطلق را نشان نمیدهد.
۲. در معادله |p|=b چرا باید مقدار b همیشه مثبت یا صفر باشد و اگر b منفی باشد چه اتفاقی میافتد؟
زیرا قدر مطلق میتواند مقدار منفی بگیرد اگر p هم منفی باشد.
چون اگر b منفی باشد تنها مقدار p=0 معادله را برقرار میکند.
چون قدر مطلق فقط خروجی مثبت یا صفر دارد و برای b منفی هیچ پاسخی ممکن نیست.
چون اگر b منفی باشد معادله بینهایت پاسخ خواهد داشت و کنترل جواب دشوار میشود.
هنگامی که مقدار b منفی باشد، به دلیل اینکه خروجی قدر مطلق هیچگاه منفی نمیشود، هیچ عددی برای p وجود ندارد که معادله را برقرار کند. پس فقط زمانی که b مثبت یا صفر باشد معادله پاسخ دارد.
۳. در حل نامعادله مطابق توضیح متن، بازه جواب چگونه تعیین میشود و هنگام حل باید به چه نکتهای توجه کرد؟
تنها باید مقدار x را از معادله 2x-4=10 پیدا کنیم و همان را بازه جواب قرار دهیم.
ابتدا نامعادله به دو نابرابری 2x-4<10 و 2x-4>-10 تبدیل و سپس بازه جواب بین دو عدد به دست میآید.
هر مقدار x که بزرگتر از صفر باشد جواب نامعادله است.
عبارت 2x-4 باید همواره مثبت باشد تا شرایط حل برقرار باشد.
برای حل نامعادله |2x-4|<10 طبق روش متن، باید دو نابرابری «2x-4<10» و «2x-4>-10» را در نظر گرفت که نتیجه آن یک بازه پیوسته برای x خواهد شد. توجه به این نکته مهم است که مقدار سمت راست یعنی عدد 10 باید مثبت باشد تا بازه جواب معتبر به دست آید.
۴. برای حل معادله طبق روش ارائهشده در آموزش، چه فرایندی لازم است؟
مقدار مطلق را حذف کرده، جواب مستقیم بنویسیم.
مقدار x را با فرض مثبت بودن عبارت داخل مطلق به دست آوریم.
معادله را به دو حالت تقسیم و برای هر جواب مقدار x را ابتدا جایگذاری و کنترل کنیم.
دو حالت برای x در نظر گرفته و هر دو را بدون بررسی استفاده کنیم.
برای حل معادلهای مانند باید آن را به دو معادله مستقل تقسیم کرد؛ یعنی یک بار با فرض مثبت بودن x-2 و بار دیگر منفی بودن آن را نوشت، سپس هر جواب به دست آمده را در معادله اصلی جایگذاری کرد و صحت جوابها را براساس شرط اولیه بررسی نمود. استفاده از جایگذاری و بررسی صحت جواب اهمیت دارد، زیرا ممکن است برخی جوابها مطابق شرایط اولیه نباشند.













سوالم این هست که حل نامعادله
|X+3|+|2x-1| کوچکتر از 6 به چه صورت هست؟
با سلام خدمت شما؛
برای حل این نامعادله ابتدا نقاط صفر شدن قدرمطلقها را پیدا میکنیم: x = -۳ و x=۱/۲. سپس محور را به سه بازه تقسیم میکنیم و در هر بازه قدرمطلقها را بدون علامت حل میکنیم. در نهایت نامعادله داده شده برای xهایی برقرار است که از ۲- بزرگتر و از ۴/۳ کوچکتراند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
بسیارعالی بود
خیلی مفید کاربردی …خیلی بهتر از بیشتر فیلم های اموزشی
سلام استاد میبخشید اگه به ما بازه جواب یه نامعادله قدر مطلقی رو بدن و بگن فرمولش رو بیان کنید از چه راهی باید استفاده کنیم
متشکرم بسیار عالی بود
سلام این درسته که “معادلات قدرمطلق میتوانند دارای یه جواب یا دو جواب باشند و یا دارای هیچ جوابی نباشند”؟
استاد خدا خیرتون بده خیلی کمکم کرد توضیحات معادلات ونامعادلات قدرمطلق
با سلام،
بله، معادله قدرمطلق ممکن است هیچ جوابی نداشته باشد. به عنوان مثال ∣x∣=−1 هیچ جوابی ندارد.
با تشکر از همراهی شما با مجله فرادرس
سلام خسته نباشید.
درمثال نامعادلات قدرمطلقی بزرگتراز b یه منفی اضافه هست لطفا اصلاح کنید که دوستان به اشتباه نیفتند.
(p≥۴)
سلام وقت بخیر ببخشید اگر در طرف قدر مطلق هم عدد داشته باشیم چی؟
یا دو قدر مطلق در یک طرف داشته باشیم؟
عالی بود . فایل پی دی اف رو هم میگزاشتید دیگه عالیتر میشد
با سلام و وقت بخیر؛
کاملا درسته. ممنون از دقت نظر شما. متن اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
در مثال آخر معادلات قدر مطلق، x = -4/3 است، اشتباه تایپ شده
با سلام،
متن، بازبینی و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس
عشقین??????
بسیار گوی و عالی بود از شما سپاسگذارم
سلام یلماز عزیز.
سپاس از همراهیتان با مجله فرادرس.
شاد و پیروز باشید.
عالي بود. ممنون از زحمات شما
سلام
اگر مثلا قدر xاز قدر y بزرگتر بود چه گونه میشود و چه شرایط دارد
ایا نامعادله
ایکس بزرگتر از ۰ و کوچکتر از ۸
هم میشه به صورت قدر مطلقی نوشت؟
سلام.
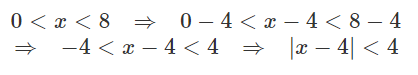
این کار بهصورت زیر قابل انجام است:
از اینکه با مجله فردارس همراه هستید، خوشحالیم.
عالی
مرسی. عالی بود