مجانب تابع – به زبان ساده
مُجانب در لغت بهمعنی «دور شونده» است و بهخاطر همین، آن را معادل واژه انگلیسی Asymptote قرار دادهاند. در فرهنگ فارسی معین این تعریف برای مجانب آمده است: «در هندسه، خط مستقیمی را مجانب یک منحنی میگویند که چون نقطهای در روی منحنی حرکت کند و به سمت بینهایت رود، فواصل این نقطه از این خط مرتب کم شود و میل به صفر کند». در این آموزش، با انواع مجانبها آشنا شده و نحوه بهدست آوردن آنها را بیان میکنیم.

مجانب چیست؟
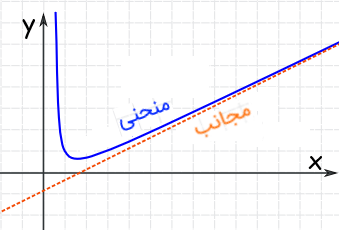
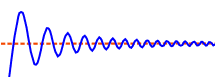
مجانب، خط راستی است که منحنی یا خمی در بینهایت به آن نزدیک میشود. شکل زیر، این موضوع را بهخوبی نشان میدهد.
همانطور که میبینیم، فاصله منحنی و مجانب با میل منحنی به بینهایت، کم و کمتر میشود.
انواع مجانبها
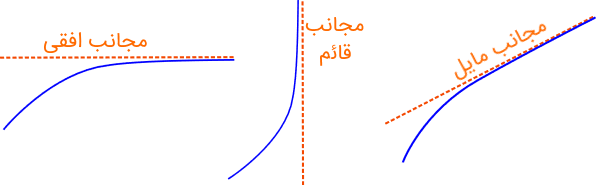
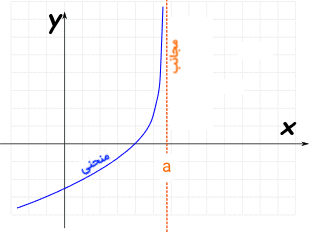
مجانب قائم
خط راست را مجانب قائم یک منحنی گوییم اگر وقتی به بینهایت میل کند، فاصله منحنی با خط به صفر برسد.
به بیان ریاضی، خط قائم یک مجانب قائم برای نمودار تابع نامیده میشود، اگر یکی از چهار شرط زیر برقرار باشد:
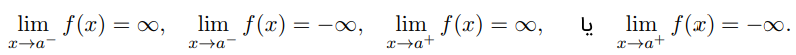
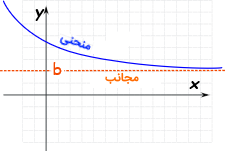
مجانب افقی
خط مجانب افقی منحنی است، اگر وقتی به بینهایت (یا منفی بینهایت) میل کند، فاصله منحنی با مقدار ثابت به صفر میل کند.
به بیان ریاضی، خط افقی ، مجانب افقی منحنی نامیده میشود، اگر یکی از دو شرط زیر برقرار باشد:
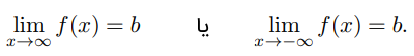
مجانب مایل
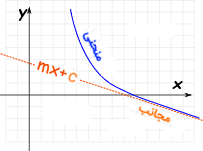
خط ، مجانب مایل است، اگر وقتی به بینهایت (یا منفی بینهایت) میل کند، فاصله منحنی و خط به صفر متمایل شود. به عبارت دیگر، خط ، مجانب مایل تابع است، اگر
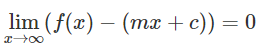
چند نکته
- یک منحنی، میتواند تعداد نامتناهی مجانب قائم داشته باشد، اما حداکثر دو مجانب افقی دارد.
- مجانبهای افقی، رفتار سمت چپ و راست منحنی را توصیف میکنند.
- اغلب، یک منحنی، با مجانب قائم برخورد نمیکند، در حالی که ممکن است از مجانب افقی عبور کند.
- مجانب افقی، نوعی مجانب مایل است که در آن، .
مجانب توابع کسری
تابع کسری زیر را در نظر بگیرید:

- مجانبهای قائم منحنی تابع ، مقادیری از خواهد بود که بهازای آنها مخرج برابر با صفر شود.
- منحنی ، حداکثر یک مجانب افقی دارد که بهصورت زیر میتوان آن را تعیین کرد:
- اگر (درجه مخرج، بزرگتر از درجه صورت باشد)، آنگاه منحنی در (یعنی محور ) یک مجانب افقی خواهد داشت.
- اگر (درجه مخرج، برابر با درجه صورت باشد)، آنگاه منحنی تابع ، یگ مجانب افقی در خواهد داشت.
- اگر (درجه صورت بزرگتر از درجه مخرج باشد)، آنگاه منحنی ، هیچ مجانب افقی نخواهد داشت.
- اگر ، مجانب مایل تابع را میتوان بهصورت تعیین کرد که در آن، درجه کوچکتر از درجه است. اگر ، میبینیم که همان شرطی که برای وجود مجانب مایل بیان کردیم، برقرار خواهد بود. مجانب مایل را میتوان از تقسیم چندجملهای صورت بر مخرج بهدست آورد.
مجانب توابع رادیکالی
وقتی ، میتوان از هم ارزیهای زیر برای توابع رادیکالی استفاده کرد:

بنابراین، میتوان مجانبها را (در صورت وجود) برای توابعی بهدست آورد که شامل توابع رادیکالی هستند.
مثالهای زیر، برای آشنایی بیشتر با نحوه تعیین مجانبهای توابع، راهگشا خواهد بود.
مثال 1
مجانبهای افقی و قائم تابع زیر را پیدا کنید:
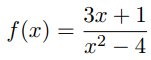
حل: مجانبهای قائم، در مقادیری از واقع هستند که مخرج تابع برابر با صفر شود:
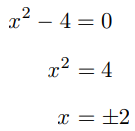
بنابراین، منحنی، دو مجانب قائم در و دارد.
مشاهده میکنید که درجه صورت از درجه مخرج بزرگتر است. بنابراین، منحنی، یک مجانب افقی در خواهد داشت. منحنی تابع بهصورت زیر است:
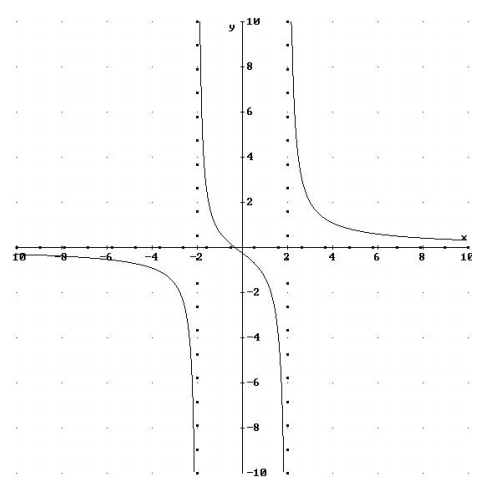
حدهای مربوط به تابع، بهصورت زیر هستند:

مثال 2
مجانبهای تابع زیر را بهدست آورید:
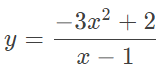
حل: از آنجایی که درجه صورت بزرگتر از درجه مخرج است، تابع فوق، مجانب افقی ندارد. اگر بخواهیم مجانب قائم تابع را بهدست آوریم، باید مخرج آن را برابر صفر قرار داده و مقداری را پیدا کنیم که بهازای آن، تابع به بینهایت میل میکند. با توجه به تابع، میبینیم که با ، تابع به بینهایت همگرا میشود، در نتیجه، ، مجانب قائم تابع است.
با توجه به اینکه درجه صورت، بهاندازه یک واحد از درجه مخرج بزرگتر است، مجانب مایل وجود دارد. گفتیم که برای بهدست آوردن مجانب مایل تابع، صورت را بر مخرج تقسیم میکنیم. بنابراین، داریم:
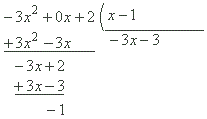
با توجه به تقسیم، میتوانیم تابع را بهصورت زیر بنویسیم:
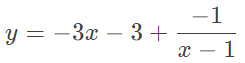
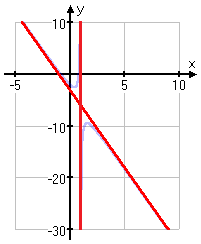
میبینیم که اگر ، کسر صفر شده و تابع به خط میل میکند. شکل زیر میل تابع به مجانب را بهخوبی نشان میدهد. خطوط قرمز رنگ، مجانبهای قائم و مایل تابع هستند.
مثال 3
مجانبهای تابع زیر را بهدست آورید:
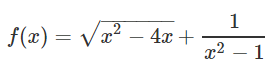
حل: طبق همارزی که برای توابع رادیکالی در بینهایت بیان کردیم، داریم:
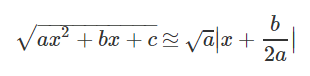
بنابراین، با میل به بینهایت، به دو مجانب مایل زیر میرسیم:
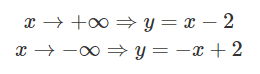













سلام تابع ثابت f(x)=b آیا مجانب افقی دارد؟ و میشه گفت خط y=b مجانب افقی این تابعه؟چون فکر میکم در شرط بالا صدق میکنه
حد این تابع وقتی مقدار xبه بینهایت میل بکنه یعنی مدام بزرگتر بشه برابر مقدار b میشه
با سلام خدمت شما؛
بله، خط y=b خطی است که نمودار تابع f(x)=b در هر دو جهت x به آن نزدیک میشود. در واقع، نمودار تابع ثابت f(x)=b خود خط y=b است. بنابراین، تابع ثابت f(x)=b دارای یک مجانب افقی در y=b است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام ایا تابع قدر مطلق xمجانب قائم افقی یا مایل داره؟
با سلام و وقت بخیر؛
خیر. تابع قدر مطلق x، مجانب قائم و افقی ندارد. مجانب قائم به حالتی اطلاق میشود که تابع به سمت بینهایت در یک نقطه خاص نزدیک میشود. تابع قدر مطلق x در نقطه x=0، تغییر شیب میدهد و به سمت بینهایت نمیرود. بنابراین، این تابع مجانب قائم ندارد. مجانب افقی به حالتی اشاره دارد که وقتی x به سمت بینهایت میل میکند، تابع به یک مقدار ثابت نزدیک میشود. وقتی تابع قدر مطلق x به بینهایت میل کند، مقدار آن نیز به بینهایت میل میکند. بنابراین این تابع، مجانب افقی نیز ندارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
ممنون از زحمات قابل ستایش تان…
بر علاوه یک سوال داشتم.
اگر صورت و مخرج با هم دو بینوم مساوی باشد. مثلا: در صورت و مخرج X-1 داشته باشیم. در این صورت مجانب قائم چی میشود؟
سلام و وقت بخیر؛
در شرایطی که صورت و مخرج یک کسر، کاملا یکسان باشند، مجانب قائمی وجود نخواهد داشت. زیرا حاصل این کسر، عدد ثابت ۱ یا y=1 خواهد بود. این معادله، یک خط افقی را نمایش میدهد که مجانب قائم ندارد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
مطالب مفید و عالی بودش ممنونم از شما
y = 2/x + 6x^2
چگونه مجانب مایل y را بدست آوریم ؟
ببخشید آقا بعضی توابع هستن در بعضی موارد هستند ک پولینومی اند ولی میبینم کتاب برایش مجانب در نظر گرفته.
آیا توابع پولینومی هم مجانب دارد یا خیر ؟
سلام
میشه مثالی از قطع مجانب قائم توسط نمودارش بگید؟این با ریشه مخرج بودن مجانب و مقدار نگرفتن تابع در آن نقطه منافات ندارد؟
سپاس از مطلب مفیدتون
سلام. ببخشید چطور توی همه موارد برای حد در بی نهایت که مجانب افقی وجود دارد متوجه بشیم که از بالا به مجانب افقی نزدیک میشود تابع یا از پایین مخصوصا در مواردی که مجانب یک عدد حقیقی غیر صفر است؟
سلام من خیلی از فرادرس راضی هستم و به دوستام هم معرفی میکنم من برای کنکور سراسری و ورود به دانشگاه میخونم و بعضی از مطالب سایتتون با اینکه فراتر از کتاب ماست ولی به فهم عمیقم تو ریاضیات خیلی کمک میکنن
سلام محدثه گرامی.
خوشحالیم که این مطلب برایتان مفید بوده است.
شاد و پیروز باشید.
سلام ،میشه به این سوال جواب بدین
تابع اف ایکس مساوی ۴ایکس به توان ۲ +ایکس-۱ به روی خط کسری ایکی به توان ۲-۲ایکس -۳ چند مجانب دارد؟
سلام علی عزیز.
تابع را میتوان اینگونه نوشت:
f(x)=x2−2x−34x2+x−1=(x−3)(x+1)4x2+x−1
همانطور که میبینیم، در x=3 و x=−1 تابع تعریفنشده است و دو مجانب قائم داریم.
حد تابع، وقتی x به بینهایت میرود، برابر با 4 است و بنابراین، یک مجانب افقی نیز داریم.
موفق باشید.
عالی ممنون واقعا
سلام.
سپاس از همراهیتان با مجله فرادرس.
شاد و پیروز باشید.
سلام خسته نباشید
من خیلی دنبال اثبات هم ارزی رادیکالی گشتم اما پیداش نکردم…میشه لطفا شما اثباتش رو بگین????
سلام مجدد.
استاد منظورم مجانب قائم هست.
امکان داره که تابعی مجانب قائم خود رو قطع کنه؟
البته چند ضابطه ای نباشه.
سلام دوباره علی عزیز.
خیر. طبق تعریف مجانب قائم، با نزدیک شدن به نقطه خاص x0، اندازه تابع به بینهایت میرود و در واقع، f(x) در x0 تعریف نشده است.
موفق باشید.
سلام.آیا تابعی میتونه مجانب خودش رو قطع کنه؟
اگر وجود داره لطفا مثال هم بزنید.
سلام.
بله، این امکان وجود دارد. برای مثال، تابع xsinx وقتی x→∞ دارای مجانب y=0 است که بارها خود تابع را قطع میکند.
سالم و موفق باشید.
سلام ببخشید چطور ثابت کنیم یک تابع حداکثر دو مجانب افقی داریم؟
سلام.
از برهان خلف میتوانید کمک بگیرید. فرض کنید تابع f(x) بیش از دو مجانب افقی داشته باشد. در این صورت،
باید علاوه بر x→∞limf(x)=a و x→–∞limf(x)=b حداقل یکی از دو تساوی x→∞limf(x)=c یا x→–∞limf(x)=d را داشته باشیم. این یعنی اینکه وقتی x به −∞ یا ∞ میل کند، دو مقدار متفاوت خواهیم داشت که با تعریف تابع تناقض دارد. بنابراین، فرض غلط است و یک تابع میتواند حداکثر دو مجانب افقی داشته باشد.
موفق باشید.
از اینکه در گسترش دانش فعالیت می کنید از شما سپاسگزاری می کنم .پرتوتن باشید ..
سلام.
خوشحالیم که این مطلب برایتان مفید بوده است.
سپاس از همراهیتان.
سلام خسته نباشید
آیا تابع میتونه روی مجانب افقی کاملا منطبق باشه؟
یا یه تابع خطی آیا مجانب مایل داره؟
سلام.برای سوال دومتون من فکر میکنم که نه توابع خطی هیچ مجانبی ندارن چون اگر دقت کنید برای مجانب داشتن تابع یا نمودار نه یک شکل خطی بلکه واضحا باید کاملا یجور منحنی و شکل انحنادار و خلاصه ” شکل غیر خطی” داشته باشن که رفته رفته نزدیک بشن به مجانب و شیبشون متغیره(مثلا در تابع هموگرافیک ، توابع کسری مجانب دار و …این حالت انحنا دار رو کاملا میشه دید) ؛
ولی توابع خطی که به فرم y=ax+b هستند دارای شیب ثابت=a هستن در همه ی نقاط دامنشون و اصلا انحنا و اون حالتی که میشه یه نمودار به مجانب نزدیک بشه رو ندارند