قاعده هوپیتال – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
در مطالب قبلی وبلاگ فرادرس، مفهوم حد در بینهایت و حد بینهایت به صورت دقیق مورد مطالعه قرار گرفت. در مثالهای موجود در این مطالب با حدهای مبهم بینهایت به روی بینهایت () و صفر به روی صفر (صفر صفرم ) مواجه شدیم که برای حل آنها از روشهای مختلف رفع ابهام مانند فاکتورگیری و اتحادها استفاده کردیم. یکی دیگر از روشهای رفع ابهام، استفاده از قاعده هوپیتال است که در این مطلب به صورت دقیق به بیان آن پرداخته میشود.


حدهای مبهم
همانطور که اشاره شد، در مطالبی مانند حد در بینهایت و حد بینهایت با کسرهایی به شکل زیر مواجه شدیم.
در حد اول موجود در رابطه فوق، اگر ما عدد را در صورت و مخرج کسر قرار دهیم، با یک عبارت مواجه میشویم. همچنین اگر در حد دوم موجود در رابطه فوق، عبارت را در صورت و مخرج جایگذاری کنیم، کسر نشان داده شده به یک کسر مبهم، تبدیل میشود.
در واقع در عبارت اول، با یک کسر مواجه هستیم که صورت و مخرج آن برابر با صفر است. در این حالت جواب کلی حد به این موضوع بستگی دارد که صفر موجود در صورت کسر بر صفر موجود در مخرج غلبه میکند و یا صفر مخرج بر صفر صورت غلبه میکند.

توجه کنید که کسر دوم یک عبارت است و بررسی آن نیز مشابه کسر اول است. در واقع پاسخ آن به این نکته بستگی دارد که بینهایت موجود در صورت کسر بر بینهایت مخرج غلبه میکند یا بینهایت موجود در مخرج بر بینهایت صورت غلبه میکند. البته حالتی نیز حضور دارد که این دو بینهایت تاثیر یکسانی دارند و در نتیجه پاسخ نهایی حد به صورت یک عدد مشاهده میشود.
مباحثی که در بالا توضیح داده شد یکی از مشکلات اصلی حالات مبهم است. در واقع در این شرایط به صورت قطعی نمیتوان درباره پاسخ یک کسر نظر داد و پاسخ هر کسر به صورت جداگانه باید مورد بررسی قرار بگیرد. در رابطه زیر، انواع حالات مبهم موجود در مبحث حد بیان شده است.
مفاهیم و قوانین مختلفی وجود دارد که به بررسی این نوع از حدها میپردازد و هرکدام از این روشها، محدودیتهایی نیز دارند. این مطلب به صورت دقیق به بررسی شیوه محاسبه حدهای مبهم بیان شده، میپردازد. البته شیوه محاسبه برخی از حدهای مبهم در مطالب قبلی وبلاگ فرادرس مورد مطالعه قرار گرفته است. برای مثال دو حد ذکر شده در ابتدای این مطلب به صورت زیر محاسبه میشوند.
در واقع کسر اول را با استفاده از نوشتن اتحاد مزدوج در صورت کسر، ساده کردیم. اتحاد مزدوج صورت کسر به صورت است. همچنین کسر دوم نیز به صورت زیر محاسبه میشود.
در محاسبه حد بالا نیز از این نکته استفاده شده که حد در بینهایت یک چند جملهای، برابر با حد بزرگترین درجه و توان آن چند جملهای است. در واقع برای اثبات این نکته میتوان از عبارت در صورت و مخرج فاکتور گرفت. این موضوع در رابطه بالا به خوبی نشان داده شده است.
بنابراین برای رفع ابهام حدهای مبهم مختلف، نیاز به استفاده از الگوهای مشخصی داریم. یکی از این الگوها و روشها برای رفع ابهام حالتهای مختلف، قاعده هوپیتال است که در بخش بعدی به صورت مفصل مورد مطالعه قرار میگیرد.

قاعده هوپیتال چیست؟
در بسیاری از مثالها و حدهایی که مشابه دو حد بیان شده در بخش قبل هستند، میتوان از روشهای ارائه شده استفاده کرد. اما این روشها برای حدهایی به شکل زیر، روشهای کارامدی نیستند.
کسر اول یک حالت مبهم صفر صفرم ( ) و کسر دوم یک حالت مبهم بینهایت به روی بینهایت ( ) را نشان میدهد. برای مثال ما نمیتوانیم عبارتی مانند را در صورت کسر دوم فاکتور بگیریم. بنابراین محاسبه آن به صورت فاکتورگیری رایج، امکان پذیر نیست و برای محاسبه آن میتوان از قاعده هوپیتال استفاده کرد. این قاعده به شکل زیر قابل بیان است.
فرض کنید که یکی از دو حالت مختلف حدهای مبهم زیر را داشته باشیم.
در روابط بالا، a میتواند هر عدد حقیقی، مثبت بینهایت و منفی بینهایت را در بر بگیرد. بنابراین تحت شرایط داده شده، رابطه زیر برقرار است.
توجه کنید که شرط مشتقپذیری توابع f و g در همسایگی محذوف نقطه a باید رعایت شود. بر این اساس و طبق رابطه بالا، قاعده هوپیتال بیان میکند که اگر ما با یکی از حالات مبهم صفر صفرم ( ) یا بینهایت به روی بینهایت ( ) مواجه شدیم، تنها کافی است که از صورت و مخرج مشتق بگیریم و حد را دوباره محاسبه کنیم.
نکته بسیار مهم دیگر این است که اگر بعد از اعمال قاعده هوپیتال، دوباره به حالتهای مبهم صفر صفرم ( ) یا بینهایت به روی بینهایت ( ) رسیدیم، کافی است که یک بار دیگر قاعده هوپیتال را اعمال و حد را محاسبه کنیم. این عمل را تا محاسبه نهایی حد و رفع ابهام کامل انجام میدهیم.
در ادامه به کمک چند مثال، کاربرد قاعده هوپیتال به صورت دقیق مورد مطالعه قرار میگیرد.
مثال 1
حد نشان داده شده در رابطه زیر را در نقطه صفر محاسبه کنید.
همانطور که مشاهده میشود، با قرار دادن مقدار صفر در صورت و مخرج رابطه فوق، کسر به صورت یک عبارت صفر صفرم در میآید.
بنابراین برای رفع ابهام حد فوق، از قاعده هوپیتال استفاده میکنیم و یک بار از صورت و مخرج آن مشتق میگیریم و حد را به شکل زیر بازنویسی میکنیم.
همانطور که مشاهده میشود، رفع ابهام به کمک قاعده هوپیتال و به صورت کامل انجام شد و پاسخ حد موجود در صورت سوال به دست آمد.

مثال 2
حد زیر را در نقطه محاسبه کنید.
در ابتدا برای محاسبه حد داده شده، مقدار را در صورت و مخرج کسر جایگذاری میکنیم. بنابراین داریم:
همانطور که مشاهده میشود، با قرار دادن مقدار در رابطه صورت سوال، حد داده شده به صورت مبهم صفر صفرم در میآید. بنابراین برای رفع ابهام کسر فوق از قاعده هوپیتال استفاده میشود.
مثال 3
حد در بینهایت زیر را محاسبه کنید.
ابتدا مقدار بینهایت را در صورت و مخرج حد فوق جایگذاری میکنیم. بنابراین داریم:
حد فوق، یک حد مبهم است و برای رفع ابهام آن از قاعده هوپیتال استفاده میکنیم. بر این اساس از صورت و مخرج مشتق میگیریم و حد را دوباره به شکل زیر محاسبه میکنیم.
همانطور که مشاهده میشود، با استفاده از قاعده هوپیتال، همچنان حد فوق به صورت بینهایت به روی بینهایت () است. بنابراین همانطور که در نکات موجود در درسنامه بیان شد، در این حالت یک بار دیگر از قاعده هوپیتال برای رفع ابهام حد داده شده استفاده میکنیم. بر این اساس از صورت و مخرج کسر فوق مشتق میگیریم و حد را مورد محاسبه قرار میدهیم. بنابراین داریم:
در نهایت همانطور که در رابطه بالا نشان داده شده، پاسخ حد فوق برابر با میشود.

رفع ابهام سایر حدهای مبهم
همانطور که اشاره شد، روش و قاعده هوپیتال برای رفع ابهام حدهای مبهم به شکل صفر صفرم () یا بینهایت به روی بینهایت () به خوبی عمل میکند. اما همانطور که در ابتدای مطلب بیان شد، حالات مبهم دیگری نیز در مبحث حد، حضور دارند. در ادامهی این مطلب به بررسی شیوه رفع ابهام سایر حدهای مبهم پرداخته میشود.
حالت مبهم
ابتدا با شیوه رفع ابهام حد مبهم صفر ضرب در بینهایت () شروع میکنیم. بنابراین در این قسمت، ابتدا باید توجه کنیم که اگر دو تابع f و g در یکدیگر ضرب شده باشند، رابطه زیر برقرار است.
در واقع با استفاده از دو رابطه بالا، میتوان یک حد به شکل را با یک حد به شکل یا جایگزین کرد و در نهایت با استفاده از قاعده هوپیتال، رفع ابهام را انجام داد. این روند در مثالهای زیر به خوبی نشان داده شده است.
مثال 1
حد زیر را محاسبه کنید.
توجه کنید که در این مثال ما مجبور هستیم که تنها حد راست عبارت فوق را در نقطه محاسبه کنیم. دلیل این موضوع این است که دامنه عبارت لگاریتمی، تنها اعداد مثبت را در بر میگیرد. دامنه و برد توابع مختلف در مطلب «دامنه و برد تابع — به زبان ساده» از مجموعه مطالب ریاضی وبلاگ فرادرس به صورت دقیق مورد مطالعه قرار گرفته است.
بنابراین با قرار دادن مقدار در رابطه صورت سوال، حالت مبهم به دست میآید. توجه کنید که قاعده هوپیتال در حالت ضرب کارایی ندارد و تنها در حالتی که یک کسر گویا داریم میتوانیم از این قاعده استفاده کنیم.
طبق توضیحات داده شده، میتوانیم حالت را به صورت یک کسر نمایش دهیم. این موضوع در رابطه زیر به خوبی بیان شده است.
حال این رابطه به یک حد مبهم تبدیل شده است. در این حالت میتوانیم از قاعده هوپیتال برای رفع ابهام آن استفاده کنیم. این موضوع در رابطه زیر نشان داده شده است.
این عبارت را میتوان به شکل زیر ساده کرد.
بنابراین رفع ابهام بیان شده به صورت کامل و با استفاده از روند بالا انجام شد.

مثال 2
حد زیر را محاسبه کنید.
همانطور که مشاهده میشود با قرار دادن مقدار بینهایت در این حد، پاسخ آن به صورت یک حالت مبهم در میآید. بنابراین با استفاده از روشی که در این بخش بیان شد، این عبارت را به صورت یک عبارت بازنویسی میکنیم. این موضوع در رابطه زیر نشان داده شده است.
بنابراین کسر فوق به صورت یک حالت مبهم صفر صفرم بازنویسی شد و برای رفع ابهام آن میتوانیم از قاعده هوپیتال استفاده کنیم.
حد فوق همچنان به صورت مبهم است. بنابراین یک بار دیگر از قاعده هوپیتال استفاده میکنیم. این موضوع در رابطه زیر نشان داده شده است.
همانطور که مشاهده میشود، در رابطه بالا، بارها از قاعده هوپیتال استفاده شده است و هر دفعه همچنان حالت مبهم وجود دارد. اما اگر حالت عکس را انجام میدادیم یعنی را در صورت و معکوس را در مخرج قرار میدادیم، حد به یک بینهایت به روی بینهایت به شکل زیر تبدیل میشود.
توجه کنید که برای نوشتن رابطه بالا از این نکته استفاده کردیم که معکوس یک عبارت نمایی برابر با توان منفی آن عبارت نمایی است. رابطه زیر به خوبی به بیان این موضوع میپردازد.
حال این عبارت بینهایت به روی بینهایت را با استفاده از قاعده هوپیتال رفع ابهام میکنیم.
در واقع همانطور که مشاهده شد، زمانی که ما حاصل ضرب داشته باشیم، میتوانیم با کمی خلاقیت، حد را به حالت مبهمی مانند صفر صفرم یا بینهایت به روی بینهایت تبدیل کنیم که قاعده هوپیتال در آن کاربرد داشته باشد. در واقع همانطور که در مثال بالا مشاهده کردیم، در برخی از حدها باید چند حالت مختلف را برای رسیدن به پاسخ صحیح در نظر بگیریم.
حالت مبهم
در ادامه به بررسی سه نوع از حالات مبهم دیگر پرداخته میشود. روند کلی این حد را میتوان با استفاده از مثال زیر به خوبی مورد بررسی قرار داد.

مثال
حد زیر را محاسبه کنید.
در ابتدا مقدار بینهایت را در متغیر این عبارت قرار میدهیم. بنابراین عبارت بالا به صورت یک حالت مبهم به شکل زیر در میآید.
برای رفع ابهام این گونه از حالات مبهم عبارت حد صورت سوال را به شکل زیر بازنویسی میکنیم.
در ادامه از طرفین رابطه فوق، لگاریتم طبیعی () میگیریم. بنابراین رابطه فوق به شکل زیر در میآید.
حال برای محاسبه حد صورت سوال، از طرفین رابطه فوق، حد در بینهایت میگیریم. بنابراین داریم:
توجه کنید که برای محاسبه حد بالا از قاعده هوپیتال استفاده شده است. در ادامه به رابطه زیر توجه کنید. این رابطه یک رابطه رایج در ریاضیات است.
در ادامه، برای محاسبه حد صورت سوال باید توجه کنید که برابر با y و عبارت y برابر با است. بنابراین رابطه زیر را داریم:
همچنین حد تابع را در قسمت قبل محاسبه کردیم. بنابراین داریم:
بنابراین همانطور که در مثالهای مختلف این مطلب مشاهده میشود، با استفاده از قاعده هوپیتال میتوان بسیاری از حدهای مبهم را مورد محاسبه قرار داد.
آزمون قاعده هوپیتال
۱. کدام یک از حالتهای حدی زیر به طور خاص مناسب استفاده از قاعده هوپیتال است؟
حالت صفر به توان صفر
حالت صفر تقسیم بر صفر
حالت صفر ضربدر بینهایت
حالت عدد تقسیم بر صفر
قاعده هوپیتال برای زمانی کاربرد دارد که صورت و مخرج به طور همزمان به صفر یا به بینهایت میل کنند. بنابراین حالت «صفر تقسیم بر صفر» دقیقا یکی از فرمهای اصلی برای استفاده از این قاعده محسوب میشود.
۲. حدود مبهم ۰ بر ۰ و بینهایت بر بینهایت چه ویژگی مشترکی دارند که باعث میشود برای تحلیل آنها از روشهای خاص مثل قاعده هوپیتال استفاده شود؟
در هر دو حالت عدد معینی به دست میآید و محاسبه آسان است.
در هر دو حالت مقدار حد به دلیل نامعین بودن نسبت تابعها قابل بهدستآوردن نیست.
در هر دو حالت، حد تابعها صرفا با سادهسازی جبری حل میشود.
در هر دو حالت همیشه میتوان بهجای تابعها فقط مقادیر حد را گذاشت.
ویژگی مشترک «نامعین بودن نسبت تابعها» در دو حالت ۰ بر ۰ و بینهایت بر بینهایت اهمیت دارد، زیرا در این شرایط مقدار دقیق حد از روی مقدار جداگانه صورت و مخرج قابل تعیین نیست و نیاز به بررسی خاص یا روشهایی مانند قاعده هوپیتال برای رفع ابهام دارد.
۳. چرا روشهای تجزیه و اتحاد مزدوج برای حل همه حدهای مبهم کافی نیستند؟
چون بعضی حدهای مبهم نیاز به تحلیل وابسته به صورت و مخرج دارند.
چون این روشها همیشه جواب صفر را تولید میکنند.
چون این روشها فقط در حدهای چندجملهای کاربرد دارند.
چون این روشها بدون مشتقگیری قابل اجرا نیستند.
روشهای تجزیه و اتحاد مزدوج تنها برای برخی اشکال ساده حدهای مبهم مناسباند و همیشه پاسخگو نیستند، چرا که بعضی حدهای مبهم بسته به ساختار صورت و مخرج نیازمند تحلیل اختصاصی هستند. این حدها گاهی با ابزارهایی قویتر مثل قاعده هوپیتال باید بررسی شوند.
۴. اگر پس از یک بار مشتقگیری روی صورت و مخرج یک حدِ مبهم از نوع همچنان ابهام باقی بماند، روش پیشنهادی قاعده هوپیتال چیست؟
بلافاصله استفاده از اتحاد مزدوج برای سادهسازی
استفاده مجدد از مشتقگیری تا رفع ابهام
تقسیم صورت بر بزرگترین توان مخرج
استفاده از تغییر متغیر روی صورت و مخرج
وقتی پس از یک بار مشتقگیری در صورت و مخرج هنوز حالت مبهم برقرار است، قاعده هوپیتال اجازه میدهد همین فرایند مشتقگیری را تکرار کنیم تا زمانیکه ابهام برطرف شود.
۵. کدام دلیل به طور دقیق نشان میدهد چرا برای حل حدهای مبهم مانند نمیتوان همیشه از آزمون و خطا استفاده کرد و باید برای هر مورد تحلیل جداگانه انجام داد؟
قاعده هوپیتال فقط برای برخی از حالات قابل استفاده است و معمولا دیگر روشها کفایت میکند.
همیشه میتوان با اتحاد مزدوج یا تجزیه، ابهام را برطرف کرد.
تمام حدهای مبهم ساختار ریاضی یکسانی دارند و راهحل عمومی دارند.
ماهیت صورت و مخرج در هر حد مبهم تفاوت دارد و نیاز به تحلیل اختصاصی دارد.
عبارت «ماهیت صورت و مخرج در هر حد مبهم تفاوت دارد و نیاز به تحلیل اختصاصی دارد» درست است چون همانطور که در متن آمده، هر حد مبهم ساختاری منحصربهفرد دارد و روشهای آزمون و خطا یا ابزارهای اولیه مانند اتحاد مزدوج همه حالات را پوشش نمیدهد.
۶. برای تبدیل یک حد مبهم به صورت به حالت قابل استفاده از قاعده هوپیتال، چه روشی مناسب است؟
به جایگذاری مستقیم مقدار حد اکتفا کنیم.
از اتحاد مزدوج برای سادهسازی استفاده کنیم.
عبارت را به صورت یک کسر بنویسیم.
مقدار حد را با مشتق مستقیم بدست آوریم.
روش درست این است که حالت ضربی مثل «عبارت را به صورت یک کسر بنویسیم» را با بازنویسی ضرب به صورت کسری مانند تبدیل کنیم، تا بتوان قاعده هوپیتال را اعمال کرد. جایگذاری مستقیم مقدار حد یا مشتقگیری بدون بازنویسی نمیتواند ابهام را رفع کند. استفاده از اتحاد مزدوج هم مختص برخی اشکال دیگر است و برای تبدیل ضرب صفر در بینهایت به فرم مناسب هوپیتال کاربرد ندارد.
۷. چرا استفاده از لگاریتم طرفین برای حدهای مبهم به شکل نمایی (مثل توابع تواندار یا نمایی) برای بهکارگیری قاعده هوپیتال کارآمد است؟
چون لگاریتمگیری توابع را به توابع چندجملهای تبدیل میکند.
چون لگاریتم طرفین معادله را به یک کسر تبدیل میکند که قابل مشتقگیری میشود.
چون لگاریتم باعث حذف نماد بینهایت میشود و همه حدها را محدود میکند.
چون لگاریتم مانع بهکارگیری قاعده هوپیتال در فرمهای کسر میشود.
روش لگاریتمگیری طرفین یک ابزار استاندارد برای حل حد نمایی نامعین است، زیرا این کار حالت ضرب یا توان نامعین را به یک کسر تبدیل میکند. در این صورت عبارت جدید به فرم مناسب قاعده هوپیتال یعنی یا میرسد و میتوان مستقیما مشتق گرفت و حد را محاسبه کرد.
۸. در کدام حالت نیاز است در روند حل یک حد مبهم با استفاده از قاعده هوپیتال، مرحله مشتقگیری دوباره تکرار شود؟
اگر پس از مشتقگیری عبارت به صورت ضربی باشد.
وقتی توابع اولیه مشتقپذیر نباشند.
اگر نتیجه حد پس از مشتقگیری صفر شود.
وقتی پس از مشتقگیری نخست ابهام حد برطرف نشده باشد.
اگر پس از یک بار مشتقگیری از صورت و مخرج هنوز عبارت حدی در حالت مبهم مثل «صفر بر صفر» یا «بینهایت بر بینهایت» باشد، باید دوباره قاعده هوپیتال را به کار برد. وجود عبارت ضربی یا مشتقپذیر نبودن توابع اولیه، دلیل تکرار مشتقگیری نیست و اگر نتیجه حد صفر شود، لزومی به ادامه روند وجود ندارد.
۹. کدام خصوصیت قاعده هوپیتال سبب میشود بتوان در حل حد مبهم بیش از یک بار از آن استفاده کرد؟
سادهسازی مستقیم کسر بدون نیاز به مشتق گیری
امکان مشتقگیری چندباره تا رفع ابهام کامل
کاربرد فقط در یک مرحله برای انواع حد مبهم
استفاده فقط برای حدهای با مخرج صفر
در قاعده هوپیتال برای بهدست آوردن حدهایی که پس از یک بار مشتقگیری هنوز مبهم باقی ماندهاند، میتوان مشتقگیری را پیاپی تکرار کرد، بنابراین تنها گزینه «امکان مشتقگیری چندباره تا رفع ابهام کامل» بیانگر این ویژگی است.












عالی بود ممنونم از شما❤
عالی
سایت شما بیش از اندازه عالیه من تمام اموزش هاتون رو میبینم
سلام
خیلی ممنون از سایت عالیتون
واقعا مفید بود??
سلام
من تا اینجایی که در مورد هوپیتال خوندم میبینم که این دو تا مثال اولی را میشد با استفاده از قاعده ی کراندار ضربدر صفر هم حل کرد
به نظرم مثالهایی میزدید که آدم ناگزیر میشد از قاعده ی هوپیتال استفاده کنه بهتر بود.
مشتق چجوری باید گرفت؟?
سلام.
برای آشنایی با مشتقگیری، آموزش «روشهای مشتقگیری — به همراه مثال» را مطالعه کنید.
از همراهی شما سپاسگزاریم.
سلام. بسیار متشکرم از توضیحات کامل شما
سلام ممنون از توضیحاتتون
در صورتی که عبارت کسری داشته باشیم که در صورت آن قدر مطلق باشد و یا عبارت کسری ای که در مخرج آن یک براکت باشد و حد یکی صفر صفرم و دیگری تعریف نشده شود از چه طریقی رفع ابهام میشود؟
مثلا
Lim ㅣx-2ㅣ تقسیم بر x-2 و x به سمت 2 میل کند.
(Lim(x-5 تقسیم بر [x-2] و x به سمت 2 میل کند
اینجا باید تو اون نقطه که ابهام ایجاد میکنه یا مخرج رو صفر میکنه، حد چپ و راست تعریف بکنید و جداگانه محاسبه کنید
سلام توضیحات کامل بود اما من این سوال را نمیتوانم حل کنم :
Lim(x+x²+…+x^n-n)/(x-1) x–>1
مرسی فیلم ها خیلی خوب بودن حد های رادیکالی رو چطور هوپیتال بگیریم؟
سلام. برای آشنایی با این موضوع، پیشنهاد میکنیم به آموزش «رفع ابهام حد — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
از همراهیتان با مجله فرادرس سپاسگزاریم.
با سلام و تشکر از بازخورد شما.
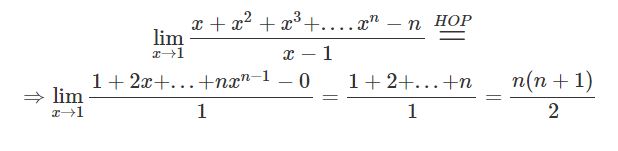
پاسخ این سوال را میتوان با استفاده از روش هوپیتال بدست آورد. در ادامه فرآیند حل این حد ارائه شده است.