تحلیل تنش و تغییر شکل در تیرها – بخش دوم: فرمول‌های متداول

در بخش اول این مقاله، به بررسی نیروها و تنش‌های برشی و خمشی درون تیرها پرداختیم. در این بخش، فهرستی از معادلات مرتبط با تغییر شکل، شیب، نیروی برشی و گشتاور خمشی موجود در امتداد تیرهای مستقیم برای شرایط مرزی و بارگذاری متفاوت آورده شده است. این فهرست، اکثر حالت‌های متداول را پوشش می دهد. از این‌رو، می توانید از آن‌ها به عنوان یک مرجع سریع برای انجام محاسبات خود و حل مسائل مربوط به تیر در مقاومت مصالح استفاده کنید.

تیرهای گیردار

در ادامه، هریک از انواع تیرهای گیردار را بررسی می‌کنیم.

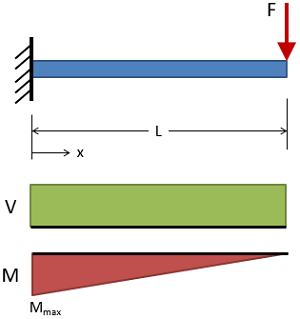
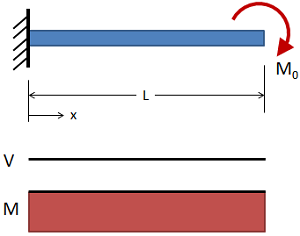
• تیرگیردار با بارگذاری انتهایی

تغییر شکل:

$$\delta = - {Fx^2 \over 6EI} \left(3L - x \right)$$

$$\delta_{max} = {F L^3 \over 3EI}\\ {x=L}$$

شیب:

$$\theta = - {Fx \over 2EI} \left(2L - x \right)$$

$$\theta_{max} = {F L^2 \over 2EI}\\ {x=L}$$

نیروی برشی:

$$V = +F$$

گشتاور خمشی:

$$M = -F (L - x)$$

$$M_{max} = -FL\\{x=0}$$

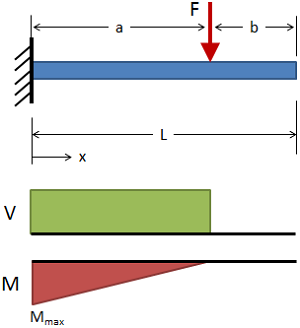
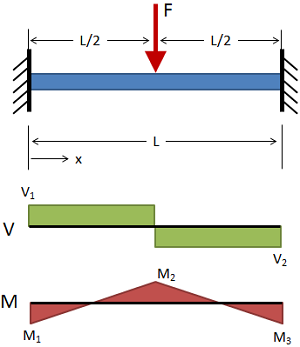
• تیرگیردار با بارگذاری میانی

تغییر شکل:

$$\delta = - {Fx^2 \over 6EI} \left(3a - x \right)\\(0 \le x \le a)$$

$$\delta = - {Fa^2 \over 6EI} \left(3x - a \right)\\(a \le x \le L)$$

$$\delta_{max} = {F a^2 \over 6EI} \left(3L - a \right)\\ {x=L}$$

شیب:

$$\theta = - {Fx \over 2EI} \left( 2a - x \right) \\ (0 \le x \le a)$$

$$\theta = - {Fa^2 \over 2EI} \\ (a \le x \le L)$$

نیروی برشی:

$$V = +F \\ (0 \le x \le a)$$

$$V = 0 \\ (a \le x \le L)$$

گشتاور خمشی:

$$M = -F (a - x) \\ (0 \le x \le a)$$

$$M = 0 \\ (a \le x \le L)$$

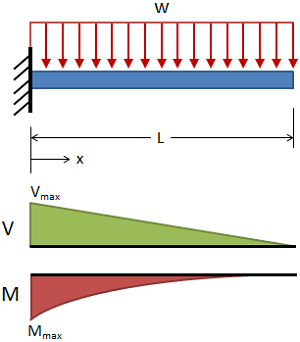
• تیرگیردار با بارگذاری یکنواخت

تغییر شکل:

$$\delta = - {w x^2 \over 24EI} \left(6L^2 - 4Lx + x^2 \right)$$

$$\delta_{max} = {w L^4 \over 8EI} \\ {x=L}$$

شیب:

$$\theta = - {wx \over 6EI} \left(3L^2 - 3Lx + x^2 \right)$$

$$\theta_{max} = {w L^3 \over 6EI} \\ {x=L}$$

نیروی برشی:

$$V = +w (L - x)$$

$$V_{max} = +wL \\ {x=0}$$

گشتاور خمشی:

$$M = -{w (L-x)^2 \over 2}$$

$$M_{max} = -{w L^2 \over 2} \\ {x=0}$$

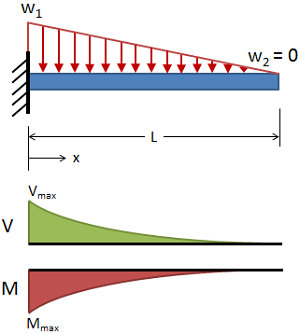
• تیرگیردار با بارگذاری یکنواخت مثلثی

تغییر شکل:

$$\delta = -{w_1 x^2 \over 120 LEI} \left(10L^3 - 10 L^2 x + 5Lx^2 - x^3 \right)$$

$$\delta_{max} = {w_1 L^4 \over 30EI} \\ {x=L}$$

شیب:

$$\theta = - {w_1 L \over 24LEI} \left(4L^3 - 6 L^2 x + 4Lx^2 - x^3 \right)$$

$$\theta_{max} = {w_1 L^3 \over 24EI} \\ {x=L}$$

نیروی برشی:

$$V_{max} = +{w_1 L \over 2} \\ {x=0}$$

گشتاور خمشی:

$$M_{max} = -{w_1 L^2 \over 6 } \\ {x=0}$$

• تیرگیردار با گشتاور انتهایی

تغییر شکل:

$$\delta = - {M_0 x^2 \over 2EI}$$

$$\delta_{max} = {M_0 L^2 \over 2EI} \\ {x=L}$$

شیب:

$$\theta = - {M_0 x \over EI}$$

$$\theta_{max} = {M_0 L \over EI} \\ {x=L}$$

نیروی برشی:

$${V = 0}$$

گشتاور خمشی:

$${M = - M_0}$$

تیرهای دوسر مفصل

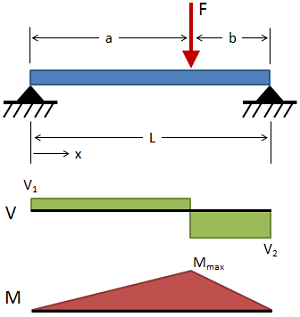
• تیر ساده با بارگذاری میانی

تغییر شکل:

$$\delta = -{Fbx \over 6LEI} \left(L^2 - b^2 - x^2 \right) \\ (0 \le x \le a)$$

برای مقادیر a بزرگتر از b داریم:

$$\delta_{max} = {Fb (L^2 - b^2)^{3/2} \over 9 \sqrt{3} LEI} \\ {x = \sqrt{ {L^2 - b^2} \over 3}}$$

شیب:

$$\theta = -{Fb \over 6LEI} \left(L^2 - b^2 - 3x^2 \right) \\ (0 \le x \le a)$$

$$\theta_1 = -{Fab (L+b) \over 6LEI} \\ {x=0}$$

$$\theta_2 = {Fab (L+a) \over 6LEI} \\ {x=L}$$

نیروی برشی:

$$V_1 = +{Fb \over L} \\ (0 \le x \le a)$$

$$V_2 = -{Fa \over L} \\ (a \le x \le L)$$

گشتاور خمشی:

$$M_{max} = +{Fab \over L} \\ {x=a}$$

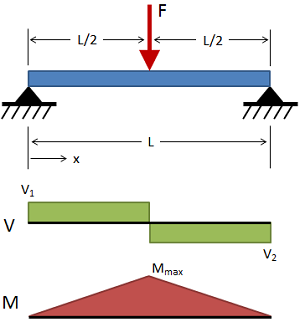
• تیر ساده با بارگذاری مرکزی

تغییر شکل:

$$\delta = -{Fx \over 48EI} \left(3L^2 - 4x^2 \right) \\ (0 \le x \le L/2)$$

$$\delta_{max} = {F L^3 \over 48EI} \\ {x=L/2}$$

شیب:

$$\theta = -{F \over 16EI} \left(L^2 - 4x^2 \right) \\ (0 \le x \le L/2)$$

$$\theta_1 = -{FL^2 \over 16EI} \\ {x=0}$$

$$\theta_2 = +{FL^2 \over 16EI} \\ {x=L}$$

نیروی برشی:

$$V_1 = +{F \over 2} \\ (0 \le x \le L/2)$$

$$V_2 = -{F \over 2} \\ (L/2 \le x \le L)$$

گشتاور خمشی:

$$M_{max} = {FL \over 4} \\ {x=L/2}$$

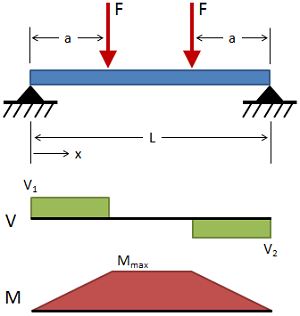
• تیر ساده با دو بارگذاری در فاصله برابر با مفصل‌ها

تغییر شکل:

$$\delta = - {Fx \over 6EI} \left(3aL - 3a^2 - x^2 \right) \\ (0 \le x \le a)$$

$$\delta = - {Fa \over 6EI} \left(3Lx - 3x^2 - a^2 \right) \\ (a \le x \le L-a)$$

$$\delta_{max} = {Fa \over 24EI} \left(3L^2 - 4a^2 \right) \\ {x=L/2}$$

شیب:

$$\theta = - {F \over 2EI} \left(aL - a^2 - x^2 \right) \\ (0 \le x \le a)$$

$$\theta = - {Fa \over 2EI} \left(L - 2x \right) \\ (a \le x \le L - a)$$

$$\theta_1 = - { Fa (L - a) \over 2EI } \\ {x=0}$$

$$\theta_2 = + { Fa (L - a) \over 2EI } \\ {x=L}$$

نیروی برشی:

$$V_1 = +F \\ (0 \le x \le a)$$

$$V_1 = -F \\ (L-a \le x \le L)$$

گشتاور خمشی:

$$M_{max} = Fa \\ (a \le x \le L - a)$$

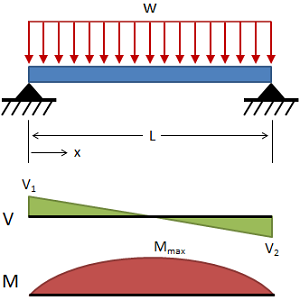
• تیر ساده با بارگذاری یکنواخت

تغییر شکل:

$$\delta = - {wx \over 24EI} \left(L^3 - 2Lx^2 + x^3 \right)$$

$$\delta_{max} = {5 w L^4 \over 384EI} \\ {x=L/2}$$

شیب:

$$\theta = - {w \over 24EI} \left(L^3 - 6Lx^2 + 4x^3 \right)$$

$$\theta_1 = -{wL^3 \over 24EI} \\ {x=0}$$

$$\theta_2 = +{wL^3 \over 24EI} \\ {x=L}$$

نیروی برشی:

$$V = w \left({L \over 2} - x \right)$$

$$V_1 = + {wL \over 2} \\ {x=0}$$

$$V_2 = - {wL \over 2} \\ {x=0}$$

گشتاور خمشی:

$$M_{max} = {w L^2 \over 8} \\ {x=L/2}$$

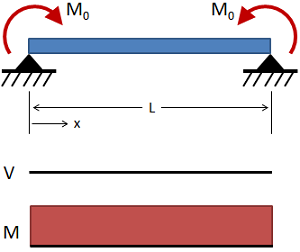
• تیر ساده با گشتاور خمشی در هر مفصل

تغییر شکل:

$$\delta = - {M_0 x \over 2EI} \left(L - x \right)$$

$$\delta_{max} = {M_0 L^2 \over 8EI} \\ {x=L/2}$$

شیب:

$$\theta = - {M_0 \over 2EI} \left(L - 2x \right)$$

$$\theta_1 = - {M_0 L \over 2EI} \\ {x=0}$$

$$\theta_2 = + {M_0 L \over 2EI} \\ {x=L}$$

نیروی برشی:

$$V=0$$

گشتاور خمشی:

$$M = M_0$$

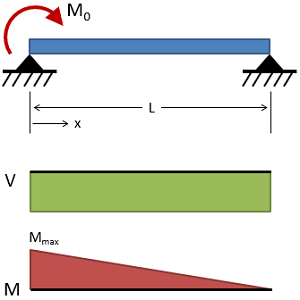
• تیر ساده با گشتاور خمشی در یک مفصل

تغییر شکل:

$$\delta = - {M_0 x \over 6LEI} \left( 2L^2 - 3Lx + x^2 \right)$$

$$\delta_{max} = {M_0 L^2 \over 9 \sqrt{3} EI} \\ x = L \left(1 - {\sqrt{3} \over 3} \right)$$

شیب:

$$\theta = - {M_0 \over 6LEI} \left(2L^2 - 6Lx + 3x^2 \right)$$

$$\theta_1 = - {M_0 L \over 3EI} \\ {x=0}$$

$$\theta_2 = + {M_0 L \over 6EI} \\ {x=L}$$

نیروی برشی:

$$V = - {M_0 \over L}$$

گشتاور خمشی:

$$M_{max} = M_0 \\ {x=0}$$

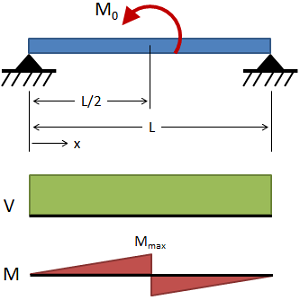
• تیر ساده با گشتاور خمشی در مرکز

تغییر شکل:

$$\delta = - {M_0 x \over 24LEI} \left(L^2 - 4x^2 \right) \\ (0 \le x \le L/2)$$

شیب:

$$\theta = - {M_0 \over 24LEI} \left(L^2 - 12x^2 \right) \\ (0 \le x \le L/2)$$

$$\theta_1 = - {M_0 L \over 24EI} \\ {x=0}$$

$$\theta_2 = - {M_0 L \over 24EI} \\ {x=L}$$

نیروی برشی:

$$V = + {M_0 \over L}$$

گشتاور خمشی:

$$M = {M_0 x \over L} \\ (0 \le x \le L/2)$$

$$M_{max} = {M_0 \over 2} \\ {x = L/2}$$

تیرهای دو انتها گیردار

در ادامه، هریک از انواع تیرهای دو انتها گیردار را بررسی می‌کنیم.

• تیر دو انتها گیرداربا بارگذاری مرکزی

تغییر شکل:

$$\delta = -{Fx^2 \over 48EI} \left(3L - 4x \right) \\ (0 \le x \le L/2)$$

$$\delta_{max} = {F L^3 \over 192EI} \\ {x = L/2}$$

نیروی برشی:

$$V_1 = +{F \over 2} \\ (0 \le x \le L/2)$$

$$V_2 = -{F \over 2} \\ (L/2 \le x \le L)$$

گشتاور خمشی:

$$M = {F \over 8} \left(4x - L \right) \\ (0 \le x \le L/2)$$

$$M_1 = M_3 = -{FL \over 8} \\ {x=0 \ و \ x=L }$$

$$M_2 = +{FL \over 8} \\ {x=L/2}$$

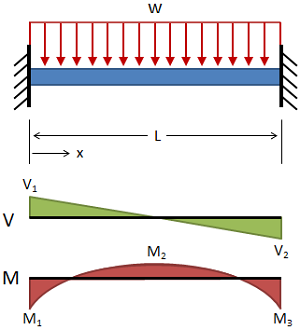
• تیر دو انتها گیردار با بارگذاری یکنواخت

تغییر شکل:

$$\delta = - {w x^2 \over 24EI} \left(L - x \right)^2$$

$$\delta_{max} = {w L^4 \over 384EI} \\ {x=L/2}$$

نیروی برشی:

$$V = w \left({L \over 2} - x \right)$$

$$V_1 = + {wL \over 2} \\ {x=0}$$

$$V_2 = - {wL \over 2} \\ {x=L}$$

گشتاور خمشی:

$$M = {w \over 12} \left(6Lx - 6x^2 - L^2 \right)$$

$$M_1 = M_3 = - {w L^2 \over 12} \\ {x=0 \ و \ x=L}$$

$$M_2 = - {w L^2 \over 24} \\ {x=L/2}$$