فرمول اصطکاک جنبشی و اصطکاک ایستایی + نمونه سوال با جواب

نیروی اصطکاک یکی از مهم‌ترین نیروهای موجود در زندگی ما است. به کمک این نیرو راه می‌رویم، بر روی کاغذ می‌نویسیم، اجسام را در دست نگه می‌داریم و بسیاری از کارهای دیگر را انجام می‌دهیم. هنگامی که توپی با سرعت معینی بر روی زمین در حال حرکت است، پس از مدت زمان مشخصی از حرکت می‌ایستد. در حالت ایده‌آل توپ به حرک خود ادامه می‌دهد زیرا هیچ نیروی خارجی بر آن وارد نمی‌شود. اما پس از مدت زمان مشخصی حرکت نخواهد کرد. این بدان معنا است که نیرویی در خلاف جهت حرکت بر توپ وارد می‌شود. به این نیرو، نیروی اصطکاک گفته می‌شود. در این مطلب از مجله فرادرس، در مورد فرمول اصطکاک ایستایی و جنبشی صحبت خواهد شد و در ادامه مثال‌هایی در مورد این دو نوع اصطکاک حل می‌شود.

فرمول اصطکاک چیست ؟

نیروی اصطکاک با حرکت اجسام مخالفت می‌کند. گرچه این نیرو منجر به تولید گرما و پوسیدگی اجسام می‌شود، اما در بیشتر موارد کمک‌کننده و لازم است. وجود این نیرو در اتومبیل‌ها منجر به اتلاف بیست درصد انرژی مفید خواهد شد. اصطکاک به نیروی عمودی سطح وابسته است. در حالت کلی این نیرو به دو قسمت تقسیم می‌شود:

1. اصطکاک ایستایی: این نوع اصطکاک از لغزیدن اجسام بر روی سطح جلوگیری می‌کند. جهت این نیرو از لغزش جسمی بر روی جسم دیگر جلوگیری خواهد کرد.
2. اصطکاک جنبشی: این نوع اصطکاک هنگامی وارد می‌شود که جسمی بر روی سطح می‌لغزد. جهت اصطکاک جنبشی با جهت اصطکاک ایستایی یکسان است.

قوانین اصطکاک چیست ؟

قوانینی بر نیروی اصطکاک حاکم هستند که مهم‌ترین آن‌ها عبارتند از:

1. اصطکاک جسم متحرک متناسب و عمود بر نیروی عمودی سطح است.
2. نیروی اصطکاک وارد شده بر جسم به ماهیت سطح در تماس با آن بستگی دارد.
3. نیروی اصطکاک مستقل از مساحت تماس است.
4. اصطکاک جنبشی مستقل از سرعت حرکت جسم است.
5. ضریب اصطکاک ایستایی از ضریب اصطکاک جنبشی بزرگتر است.

فرمول اصطکاک ایستایی چیست ؟

اگر جسم ساکنی بر روی سطحی مانند میز یا زمین قرار داشته باشد، از طرف سطح نیرویی عمودی و رو به بالا بر آن وارد می‌شود. فرمول اصطکاک ایستایی از حاصل‌ضرب نیروی عمودی سطح در ضریبی به نام ضریب اصطکاک ایستایی به دست می‌آید و به صورت زیر نوشته خواهد شد:

$$f_s \leq \mu_s N$$

فرمول اصطکاک جنبشی چیست ؟

در حالتی که جسم حرکت می‌کند، فرمول اصطکاک جنبشی از حاصل‌ضرب نیروی عمودی سطح در ضریبی به نام ضریب اصطکاک جنبشی به دست می‌آید و به صورت زیر نوشته می‌شود:

$$f_s = \mu_k N$$

ضریب اصطکاک با استفاده از رابطه زیر محاسبه خواهد شد:

$$\frac{f}{N}= \mu$$

در رابطه فوق، f نیروی اصطکاک و N نیروی عمودی سطح است.

مثال‌ های فرمول اصطکاک ایستایی و جنبشی

تاکنون با فرمول اصطکاک جنبشی و ایستایی آشنا شدیم. در ادامه، به منظور درک بهتری از فرمول اصطکاک و نحوه استفاده از آن در مسائل فیزیک، مثال‌های گوناگونی حل خواهد شد.

مثال ۱

پالت چوبی با بار ۶۰۰ کیلوگرم بر روی سطح چوبی در حال سکون قرار دارد.

(۱)‌ راننده جرثقیلی تصمیم می‌گیرد پالت چوبی را بدون بلند کردن، هل دهد. چه نیرویی برای به حرکت درآوردن آن باید اعمال شود؟

(۲) پس از گذشت مدت زمان کوتاه، پالت شروع به لغزیدن می‌کند. اگر پالت تحت‌تاثیر نیروی محاسبه شده در قسمت (۱) حرکت کند، پس از گذشت نیم ثانیه سرعت آن چه مقدار خواهد بود؟

(۳) اگر نیروی وارد شده از طرف جرثقیل حذف شود، پالت چه مسافتی را قبل از ایستادن طی خواهد کرد؟

پاسخ

چهار نیرو بر پالت وارد می‌شوند:

• نیروی وزن به سمت پایین
• نیروی عمودی سطح به سمت بالا
• نیروی رو به جلوی وارد شده از طرف جرثقیل
• نیروی اصطکاک در خلاف جهت حرکت

از آنجایی که سطح افقی است، نیروی عمودی سطح و نیروی وزن با هم برابر هستند. اصطکاک از ایستایی به جنبشی تغییر خواهد کرد. ذکر این نکته مهم است که در ابتدا نیروی اصطکاک ایستایی بر پالت وارد می‌شود. همچنین، مقدار نیروی وارد شده از سمت جرثقیل در ابتدا برابر صفر است. سپس، به مقدار مشخصی افزایش می‌یابد و در ادامه، پس از ۰/۵ ثانیه از شروع حرکت، مقدار آن صفر خواهد شد.

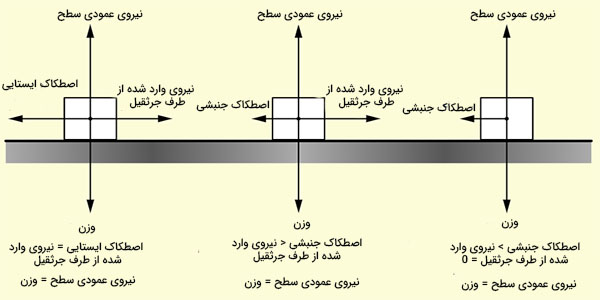
قسمت (۱): برای آن‌که پالت شروع به حرکت کند، راننده جرثقیل باید نیرویی برابر با مقدار بیشینه اصطکاک ایستایی بر آن وارد کند:

$$P = f_s = \mu_s N = \mu_s mg\\ P = (0.28)(600 \ kg)(9.8 \ \frac{m}{s^2}) \\ P= 1646 \ N$$

قسمت (۲): هنگامی که پالت شروع به حرکت می‌کند، مقدار ضریب اصطکاک از ایستایی به جنبشی کاهش می‌یابد:

$$f_k = \mu_k n = \mu_k mg \\ f_k = (0.17)(600 \ kg) (9.8 \ \frac{m}{s^2}) \\ f_k = 1000 \ N$$

اما جرثقیل هنوز پالت را با نیروی ۱۶۴۶ نیوتن هل می‌دهد. بنابراین نیروی خالص کل غیرصفر است.

$$\sum F = P-f_k \\\sum F = 1646 \ N -1000 \ N \\\sum F = 646 \ N$$

نیروی خالص غیرصفر سبب حرکت شتاب‌دار خواهد شد. بنابراین داریم:

$$a = \frac{\sum F }{m} \\ a = \frac{(646 \ N)}{600 \ kg} \\ a = 1.08 \frac{m}{s^2}$$

برای به دست آوردن سرعت حرکت جسم پس از گذشت ۰/۵ ثانیه، از رابطه سرعت بر حسب زمانِ حرکت بر خط راست برای حرکت با شتاب ثابت استفاده می‌کنیم:

$$v = v_0 + at \\ v = (1.08 \ \frac{m}{s^2}) (0.5 \ s) \\ v = 0.54 \ \frac{m}{s}$$

قسمت (۳): هنگامی که نیروی وارد شده از سمت جرثقیل حذف می‌شود، نیروی خالص کل برابر نیروی اصطکاک جنبشی خواهد شد. این نیروی کل شتابی در خلاف جهت حرکت ایجاد می‌کند. هنگامی که دو بردار در خلاف جهت یکدیگر قرار داشته باشند، یکی از آن‌ها باید منفی شود. در این مثال، نیروی اصطکاک را منفی در نظر می‌گیریم:

$$a= \frac{\sum F}{m} = \frac{f_k}{m} \\ a =\frac{ ( -1000 \ N)}{(600 \ kg)} \\ a = -1.67 \ \frac{m}{s^2}$$

برای به دست آوردن مسافت طی شده توسط پالت از رابطه زیر استفاده می‌کنیم:

$$v^2 = v_0^2 + 2a \triangle x$$

سرعت نهایی برابر صفر است.

$$\triangle x = \frac{-v_0^2}{2a} \\ \triangle x = \frac{-(0.54 \ \frac{m}{s})^2}{2 ( -1.67 \ \frac{m}{s^2})} \\ \triangle x = 0.087 \ m$$

مثال ۲

اتومبیلی در جاده مسطحی با ضریب اصطکاک ایستایی ۰/۷۵ ($$\frac{3}{4}$$) و ضریب اصطکاک جنبشی ۰/67 ($$\frac{2}{3}$$) در حال حرکت است. مطلوب است:

(۱) بیشینه شتاب شروع حرکت اتومبیل را با در نظر گرفتن حرکت سریع و غیرسریع به دست آورید. چگونه این دو شروع حرکت اتومبیل با یکدیگر مقایسه می‌شوند؟ منظور از شروع حرکت سریع آن است که رد لاستیک‌ها بر روی آسفالت باقی بماند.

(۲) بیشینه فاصله‌ای که اتومبیل پس از ترمز طی می‌کند را به دست آورید. در این قسمت نیز دو نوع ترمز معمولی و ضدقفل را در نظر بگیرید. چگونه این دو نوع ترمز اتومبیل با یکدیگر مقایسه می‌شوند؟

پاسخ

قسمت (۱): نیروی خارجی کل که ماشین را به سمت جلو سوق می‌دهد، نیروی اصطکاک بین لاستیک‌ها و آسفالت است. هنگامی که راننده پای خود را به شدت بر روی پدال گاز فشار می‌دهد، لاستیک‌ها بر روی سطح جاده گیر می‌کنند و دودی در محل تماس لاستیک‌ها با آسفالت ایجاد می‌شود. از آنجایی که لاستیک‌ها می‌لغزند، ضریب اصطکاک ایستایی شتاب بیشینه را تعیین می‌کند.

اما در حالت عادی، بیشتر راننده‌ها به آرامی اتومبیل را به حرکت در می‌آورند. در نتیجه، لاستیک‌ها بر روی سطح بدون لغزش می‌چرخند. بنابراین، ضریب اصطکاک ایستایی بیشینه شتاب اتومبیل را تعیین خواهد کرد.

برای حل این قسمت، نیروی اصطکاک را برابر نیروی خالص کل قرار می‌دهیم. در نتیجه، بر طبق قانون دوم نیوتن داریم:

$$\sum F = ma \\ f = \mu mg = ma \\ a = \mu g$$

برای شتاب حرکت بسیار سریع داریم:

$$a_{burnout} = \frac{2}{3} (9.8 \ \frac{m}{s^2}) = 6.54 \ \frac{m}{s^2}$$

برای شتاب حرکت آرام داریم:

$$a_{normal} = \frac{3}{4} (9.8 \ \frac{m}{s^2}) = 7.35 \ \frac{m}{s^2}$$

نسبت این دو شتاب برابر است با:

$$\frac{a_{burnout}}{a_{normal}} = \frac{\mu _k g}{\mu _s g}= \frac{\mu _k }{\mu _s} = \frac{\frac{2}{3}}{\frac{3}{4}} = \frac{8}{9} = 8.89$$

برخلاف باور عموم، فشردن شدید پا بر روی پدال گاز به هنگام به حرکت در آوردن اتومبیل روش موثری برای شروع حرکت نیست. شروع سریع حرکت، تنها در حدود 90 درصد شروع معمولی اتومبیل موثر است.

قسمت (۲): نیروی اصطکاک بین لاستیک‌ها و آسفالت، نیروی خالص کلِ متوقف کننده اتومبیل است. توقف اتومبیل با ترمز معمولی سبب قفل شدن چرخ‌ها می‌شود. بنابراین، چرخ‌ها قادر به چرخش نخواهند بود. در این حالت، چرخ‌ها سر می‌خورند. ضریب اصطکاک جنبشی، فاصله طی شده بعد از ترمز را تعیین خواهد کرد.

بیشتر اتومبیل‌ها مجهز به سیستم ترمز ضدقفل (ABS) هستند. سنسور تعبیه شده در این سیستم، پدال ترمز را به هنگام قفل شدن چرخ‌ها رها می‌کند. پس از مکثی کوتاه، ترمز به سرعت دوباره درگیر خواهد شد. در صورت قفل نشدن مجدد چرخ‌ها، همه چیز خوب است. اما در صورتی که چرخ‌ها مجدد قفل شوند، ABS پدال ترمز را مجدد رها می‌کند. این روند در یک ثانیه به تعداد زیادی تکرار خواهد شد. در هر صورت، چرخ‌ها بیشتر از میلی‌ثانیه قفل نمی‌شوند. اتومبیل با استفاده از نیروی اصطکاک ایستایی متوقف خواهد شد.

برای حل این قسمت، از رابطه جابجایی بر حسب سرعت استفاده می‌کنیم.

$$v_0^2 = 2a \triangle x = 2 \mu g \triangle x \\ \triangle x = \frac{v^2}{2 \mu g} \\ \frac{\triangle x_{antilock}}{\triangle x_{normal}} = \frac{\frac{v_0^2}{2 \mu_s g} }{\frac{v_0^2}{2 \mu_k g} } = \frac{\mu_k}{\mu_s}= \frac{\frac{2}{3}}{\frac{3}{4}} = \frac{8}{9}= 8.89$$

مسافت طی شده توسط اتومبیل پس از ترمز ضدقفل در حدود ۹۰ درصد مسافت طی شده پس از ترمز معمولی است.

مثال ۳

نیرویی برابر ۱۰ نیوتن بر آجری به جرم ۲ کیلوگرم وارد می‌شود. اگر آجر بر روی سطح زبری قرار داشته باشد، مطلوب است:

(۱)‌ مقدار نیروی اصطکاک. فرض کنید ضریب اصطکاک جنبشی بین آجر و سطح برابر ۰/۲۴ است.

(۲) نیروی خالص کل وارد شده بر آجر را به دست آورید.

(۳) شتاب حرکت آجر را به دست آورید.

پاسخ

همان‌گونه که در توضیحات فوق عنوان شد، نیروی اصطکاک جنبشی در خلاف جهت حرکت جسم بر آن وارد می‌شود. فرمول اصطکاک جنبشی برابر است با:

$$f_k = \mu_k N$$

قسمت (۱): آجر در راستای عمود حرکت نمی‌کند یا از روی سطح بلند نمی‌شود. بنابراین، نیروهای وارد شده در راستای عمودی یکدیگر را خنثی می‌کنند. نمودار جسم آزاد در تصویر زیر نشان داده شده است. در راستای عمود، دو نیروی عمودی سطح و وزن، بر آجر وارد می‌شوند.

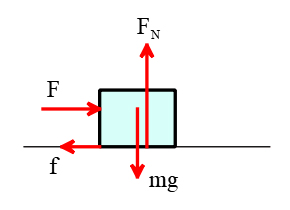
از آنجایی که نیروهای عمودی یکدیگر را خنثی می‌کنند، داریم:

$$N = mg = 2 \times 10 = 20 \ N$$

با دانستن مقدار نیروی عمودی سطح، مقدار نیروی اصطکاک جنبشی را به دست می‌آوریم:

$$f_k = \mu_k N = 0.24 \times 20 = 4.8 \ N$$

قسمت (۲): نیروی خالص به معنای جمع برداری نیروها است. در راستای افقی، دو نیرو بر آجر وارد می‌شوند:

1. نیروی خارجی F.
2. نیروی اصطکاک جنبشی.

این دو نیرو در خلاف جهت یکدیگر قرار دارند. تفاضل این دو نیرو برابر نیروی خالص وارد شده بر آجر است:

$$F_{net} = F - f_k = 10 - 4.8 = 5.2 \ N$$

قسمت (۳): بر طبق قانون دوم نیوتن، اگر نیروی ‌F بر جسمی به جرم‌ m وارد شود، شتاب حرکت آن برابر با $$a= \frac{F}{m}$$ خواهد بود. در نتیجه، شتاب حرکت آجر برابر است با:

$$a= \frac{F_{net}}{m} = \frac{4.8}{2} = 2.4 \ \frac{m}{s^2}$$

مثال ۴

برای به حرکت درآوردن جعبه‌ ساکنی به جرم ۶ کیلوگرم که بر روی سطح سیمانی قرار دارد، اعمال نیرویی برابر ۳۵ نیوتن موازی با سطح لازم است.

(۱) ضریب اصطکاک ایستایی بین آجر و سطح را به دست آورید.

(۲)‌ با نگه داشتن این نیرو، جعبه با شتاب ۰/۶ متر بر مجذور ثانیه حرکت می‌کند. مقدار ضریب اصطکاک جنبشی را به دست آورید.

پاسخ

فرمول اصطکاک ایستایی مانند فرمول اصطکاک جنبشی ثابت نیست. مقدار این اصطکاک با توجه به اندازه نیروی خارجی تغییر می‌کند. اما مقدار بیشینه‌ای برای اصطکاک ایستایی وجود دارد. اگر اندازه نیروی خارجی از این مقدار بیشینه زیادتر باشد، جسم شروع به حرکت خواهد کرد. مقدار بیشینه اصطکاک ایستایی برابر است با:

$$f_{smax} = \mu_s N$$

قسمت (۱): جعبه بر روی سطح افقی قرار دارد و نیرویی موازی سطح بر آن وارد می‌شود. بنابراین، نیروی عمودی سطح برابر است با:

$$N= mg = 6\times 10 = 60 \ N$$

در این مثال، جسم در ابتدا ساکن است. بنابراین، نیروی اصطکاک از نوع ایستایی است. مقدار بیشینه این نیرو عبارت است از:

$$f_{smax} = \mu_s N$$

با اعمال نیروی ۳۵ نیوتن، جعبه در آستانه حرکت قرار می‌گیرد. بنابراین، بیشینه نیروی اصطکاک ایستایی برابر ۳۵ نیوتن خواهد بود:

$$f_{smax} = F \\ \mu_s N = F \\ \Rightarrow \mu_s = \frac{F}{N} \\ = \frac{35}{70} = 0.5$$

قسمت (۲): اگر نیروی ثابت وارد شده پس از حرکت جعبه حذف نشود، نیروی اصطکاک ایستایی به جنبشی تبدیل خواهد شد. از آنجایی که جعبه با شتاب ثابت حرکت می‌کند، نیروی خالص کل مخالف صفر است. نیروی خارجی اعمال شده بر جعبه در راستای حرکت آن وارد می‌شود. اما، اصطکاک خلاف جهت حرکت جعبه است. در نتیجه، نیروی خالص کل برابر تفاضل نیروی خارجی و اصطکاک خواهد بود:

$$F_{net} = F - f_k = F - \mu_kN$$

جعبه بر روی سطح افقی قرار دارد و در این راستا با شتاب ثابت حرکت می‌کند. بنابراین، نیروهای وارد شده در راستای عمودی یکدیگر را خنثی می‌کنند.

$$N= mg = 7 \times10 = 70 \ N$$

بر طبق قانون دوم نیوتن، داریم:

$$F_{net} = ma \\ F - \mu_k (mg) = ma \\ \Rightarrow \mu_k = \frac{F - ma}{mg} \\ = \frac{35 - 7}{7\times 10} = 0.44$$

همان‌گونه که انتظار می‌رفت، ضریب اصطکاک ایستایی بزرگ‌تر از ضریب اصطکاک جنبشی است.

مثال‌های زاویه اصطکاک

پس از حل مثال‌های مربوط به فرمول اصطکاک جنبشی و ایستایی، مثال‌هایی در رابطه با زاویه اصطکاک حل خواهیم کرد.

مثال اول زاویه اصطکاک 

در این مثال در مورد زاویه اصطکاک صحبت می‌کنیم. جمع برداری نیروی اصطکاک و نیروی عمودی سطح با ‌R نشان داده می‌شود.

$$R = \sqrt{N^2 + f^2}$$

زاویه اصطکاک برابر با زاویه بین ‌R و نیروی عمودی سطح یعنی ‌N است.

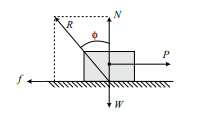
$$\phi$$ زوایه اصطکاک است.

$$tan\phi = \frac{f}N \\ \phi = tan^{-1}\frac{f}{N}$$

مثال دوم زاویه اصطکاک

سطح شیب‌داری را در نظر بگیرید که جسمی به وزن W بر روی آن در حالت سکون قرار دارد.

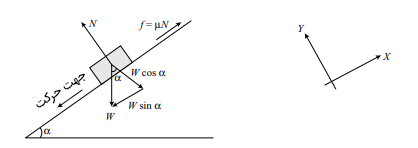
سطح شیب‌دار با افق زاویه $$\alpha$$ ساخته است. نیروهای وارد شده بر جسم عبارتند از:

1. وزن جسم. این نیرو دو مولفه دارد: $$Wsin\alpha$$ موازی سطح شیب‌دار و $$Wcos\alpha$$ عمود بر سطح شیب‌دار.
2. نیروی عمودی سطح که موازی سطح شیب‌دار است.
3. نیروی اصطکاک که خلاف جهت حرکت جسم و موازی سطح شیب‌دار است.

هنگامی که جسم تمایل دارد از بالای سطح شیب‌دار به سمت پایین حرکت کند، نیروی اصطکاک موازی سطح شیب‌دار و به سمت بالا وارد می‌شود. به هنگام حرکت جسم به بالای سطح شیب‌دار، نیروی اصطکاک موازی سطح و به سمت پایین وارد می‌شود.

همان‌گونه که در تصویر نشان داده شده است، دستگاه مختصات را به گونه‌ای انتخاب می‌کنیم که محور x موازی سطح شیب‌دار و محور y، عمود بر آن باشد.

اگر جسم با سرعت ثابت حرکت کند، داریم:

$$\sum F_x = 0 \\ f = Wsin\alpha \\ \sum F_y = 0\\ N= Wcos\alpha \\ \frac{f}{N}= \frac{W sin \alpha}{W cos \alpha}= tan \alpha\\$$

اما، با توجه به مثال اول زاویه اصطکاک داریم:

$$\frac{f}{N} = \mu = tan\phi$$

که $$\phi$$ برابر زاویه اصطکاک است.

مثال دوم زاویه اصطکاک

حرکت جسمی بر روی سطح زبری را در نظر بگیرید. برای حرکت جسم دو حالت کلی وجود دارد. در مورد شرط برقراری تعادل برای هر حالت به طور جداگانه بحث خواهد شد.

حالت (۱)

در حالت (۱)، هیچ نیرویی به جسم وارد نمی‌شود. در نتیجه، جسم در راستای افقی یا عمودی حرکتی نخواهد داشت.

$$P = 0 \\ f = 0\\ W = N$$

حالت (۲)

در این حالت، نیروی P بر جسم وارد می‌شود. نمودار جسم آزاد در تصویر زیر نشان داده شده است.

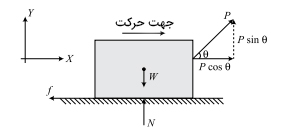
اگر جسم در حالت سکون باشد یا با سرعت ثابت حرکت کند، برآیند نیروهای وارد بر آن در دو راستای x و y برابر صفر خواهد بود:

$$\sum F_x = 0 \\ Pcos\theta = f \ (f=\mu N)\\ Pcos\theta = \mu N \ (1)\\ \sum F_y = 0 \\ N = W\pm Psin\theta \\ W = N + Psin\theta \\ N = W - Psin\theta \ (2)$$

از رابطه‌های (۱)‌ و (۲)‌ داریم:

$$Pcos\theta = \mu(W-Psin\theta) \\ Pcos\theta + \mu P sin\theta = \mu N \\ P(cos\theta + \frac{sin\phi}{cos\phi} sin\theta) = \frac{sin\phi}{cos\phi} \ W \\ P(cos\theta cos \phi \ + \ sin\theta sin\phi) = W sin\phi \\ Pcos (\theta - \phi) = Wsin\phi \\ P = \frac{Wsin\phi}{cos (\theta - \phi)}$$

اگر بخواهیم نیروی P کمینه باشد، $$cos (\theta - \phi)$$ باید بیشینه باشد:

$$cos (\theta - \phi) = 1\\ \theta = \phi$$

زاویه نیروی P با سطح افقی باید برابر زاویه اصطکاک باشد.

مثال سوم زاویه اصطکاک

جعبه‌ای به وزن ۵ کیلونیوتن توسط نیروی P کشیده می‌شود. ضریب اصطکاک بین جعبه و سطح برابر ۰/۳۵ است. زاویه $$\theta$$ هنگامی که مقدار نیروی P کمینه است و مقدار P را به دست آورید.

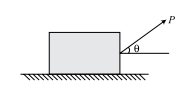
پاسخ

در ابتدا نمودار آزاد جسم را رسم می‌کنیم.

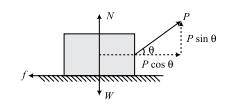
تعادل به شرط زیر برقرار است:

$$\sum F_x = 0\\ f= Pcos \theta \\ \sum F_y = 0 \\ W = N + P sin\theta$$

اگر نیروی P کمینه باشد، زاویه $$\theta$$ برابر با زاویه اصطکاک خواهد بود:

$$\theta = \phi \ tan^{-1} \mu = tan^{-1} 0.35 \\ = 20.48^o \\ P = \frac{Wsin\phi}{cos(\theta - \phi)}$$

برای آن‌که نیروی ‌P کمینه باشد، مقدار $$cos(\theta - \phi)$$ باید برابر یک باشد. در نتیجه، برای نیروی P داریم:

$$P = Wsin\phi = 5 sin \ 20.48^o= 1.75 \ kN$$

مثال چهارم زاویه اصطکاک

در این مثال، در مورد سطح شیب‌دار زبر صحبت خواهیم کرد. سه حالت کلی تعادل، حرکت جسم به سمت پایین و حرکت جسم به سمت بالا را در نظر می‌گیریم.

حالت تعادل

قسمت (۱): زاویه سطح ‌شیب‌دار کمتر از زاویه اصطکاک است. نمودار جسم آزاد در تصویر زیر نشان داده شده است.

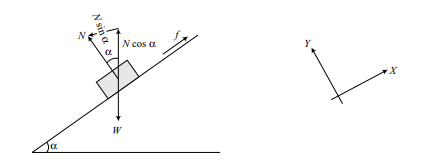
شرط تعادل را می‌نویسیم:

$$\sum F_x = 0 \\ f = \mu N = N sin\alpha \\ \sum F_y =0 \\ W = Ncos\alpha$$

جسم در حال تعادل است.

قسمت (۲): زاویه سطح شیب‌دار از زاویه اصطکاک بیشتر است. جسم به سمت پایین حرکت می‌کند. بنابراین، نیروی رو به بالای P برای جلوگیری از حرکت جسم به سمت پایین لازم است. این نیرو می‌تواند به صورت‌های متفاوتی اعمال شود:

۱. در امتداد سطح شیب‌دار:

در این حالت، نمودار جسم آزاد را به صورت زیر رسم می‌کنیم:

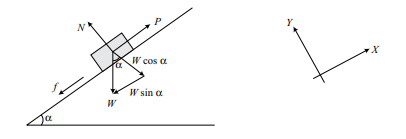
از آنجایی که نیروی P به سمت بالا بر جسم وارد شده است و از حرکت رو به پایین آن بر روی سطح شیب‌دار جلوگیری می‌کند، بنابراین حالت تعادل برقرار خواهد بود:

$$\sum F_x = 0 \\ f = P - W sin\alpha \\ \sum F_y =0 \\ N = Wcos\alpha$$

۲. نیروی P در راستای افق بر جسم وارد می‌شود:

نمودار جسم آزاد در ادامه نشان داده شده است.

شرط تعادل به صورت زیر برای جسم برقرار خواهد بود:

$$\sum F_x = 0 \\ f = P cos \alpha- W sin\alpha \\ \sum F_y =0 \\ N = Wcos\alpha + P sin \alpha$$

۳. نیروی P با زاویه $$\theta$$ نسبت به سطح شیب‌دار بر جسم وارد شده است:

برای این حالت، نمودار جسم آزاد به صورت زیر رسم شده است.

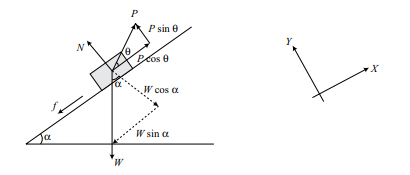
شرایط تعادل در دو راستای x و y به صورت زیر برقرار هستند:

$$\sum F_x = 0 \\ f = P cos \theta- W sin\alpha \\ \sum F_y =0 \\ N = Wcos\alpha - P sin \theta$$

لغزش به سمت پایین

جسمی به وزن ‌W بر روی سطح شیب‌دار قرار دارد و در آستانه لغزش به سمت پایین قرار دارد. نیروی کمینه P برای توقف جسم لازم است. در ابتدا نمودار آزاد جسم را رسم می‌کنیم و سپس شرایط تعادل را می‌نویسیم.

$$\sum F_x = 0 \\ f =\mu N = W sin\alpha - P \ (1) \\ \sum F_y =0 \\ N = Wcos\alpha \ (2)$$

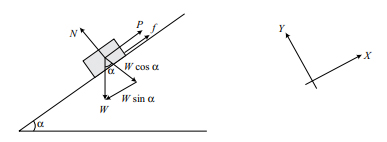
از معادلات (۱) و (۲) داریم:

$$P = Wsin\alpha - \mu(W cos\alpha) \\ = W( sin\alpha - \mu cos\alpha) \\ = W(sin\alpha - \frac{sin \phi}{sin \theta}cos \alpha) \\ \mu = tan\phi = \frac{sin\phi}{cos\phi}\\ Pcos\phi = W(sin\alpha cos \phi - cos\alpha cos\phi) \\ P = \frac{W sin(\alpha - \phi)}{cos \phi}$$

حرکت به سمت بالا بر روی سطح شیب دار

هنگامی که جسم بر روی سطح شیب‌دار به سمت بالا حرکت می‌کند، برای توقف آن به نیروی کمینه P نیاز است. در ابتدا نمودار جسم آزاد را رسم می‌کنیم و در ادامه شرایط برقراری تعادل را می‌نویسیم.

$$\sum F_x = 0 \\ f = P - W sin\alpha \\ P=W\sin\alpha +f = Wsin \alpha +\mu N \ (1) \\ \sum F_y =0 \\ N = Wcos\alpha \ (2)$$

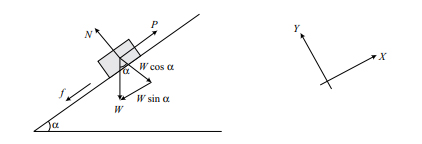
از رابطه‌های (۱) و (۲) داریم:

$$P = Wsin\alpha + \mu(W cos\alpha) \\ = W sin\alpha + \frac{\sin \phi}{cos \phi}cos\alpha \ [\mu =tan\phi = \frac{sin\phi}{cos\phi}]\\ P cos\phi= Wsin\alpha cos \phi +W cos\alpha sin\phi) \\ = W sin (\alpha + \phi) \\ P = \frac{Wsin(\alpha + \phi)}{cos \phi}$$

مثال پنجم زاویه اصطکاک

جسمی به وزن ۵۰۰ نیوتن بر روی سطح شیب‌داری با زاویه ۳۰ درجه قرار گرفته است و توسط نیروی P موازی سطح به سمت بالا کشیده می‌شود. اگر ضریب اصطکاک بین جسم و سطح برابر ۰/۳ باشد، نیروی وارد شده بر جسم را به دست آورید.

پاسخ

در ابتدا نمودار آزاد جسم را رسم می‌کنیم:

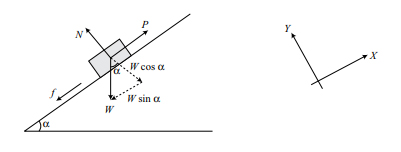
داده‌های مثال عبارتند از:

$$W = 500 \ N\\ \alpha = 30^o \\ \mu = 0.3$$

زاویه اصطکاک به صورت زیر به دست می‌آید:

$$\phi = tan^{-1}\mu = tan^{-1} 0.3 = 16.7^o$$

نیروی اصطکاک به سمت پایین بر جسم وارد خواهد شد. زیرا جسم تمایل به حرکت به سمت بالا دارد. اگر نیروی کمینه P را به سمت بالا بر جسم وارد کنیم، حالت تعادل برقرار خواهد بود:

$$\sum F_x = 0 \\ f = P - W sin\alpha = f = \mu N \\ P= Wsin \alpha +\mu N \ (1) \\ \sum F_y =0 \\ N = Wcos\alpha \ (2)$$

با استفاده از معادلات (۱) و (۲) داریم:

$$P = Wsin\alpha + \mu Wcos \alpha \\ = 500 \ sin30^o+ 0.3 \ \times 500 \ \times \ cos 30^o \\ = 250 \times0.5 + 0.3 \times 500\times 0.866 \\ = 250 + 129.9 = 379.9 \ N$$

مثال ششم زاویه اصطکاک

جسمی به وزن W بر روی سطح شیب‌دار زبری با زاویه $$\alpha$$ نسبت به افق قرار گرفته است. نیروی P به صورت افقی بر آن وارد می‌شود. اگر جسم در آستانه حرکت به سمت بالای سطح شیب‌دار قرار داشته باشد، ثابت کنید نیروی‌ P با استفاده از رابطه زیر به دست خواهد آمد:

$$P = W tan (\alpha + \phi)$$

در رابطه بالا $$\phi$$ زاویه اصطکاک است.

پاسخ

ابتدا نمودار جسم آزاد را رسم می‌کنیم:

$$\sum F_x = 0 \\ P cos \alpha = W sin\alpha + f = W sin\alpha + \mu N \ (1) \\ \sum F_y =0 \\ N = Wcos\alpha + Psin \alpha \ (2)$$

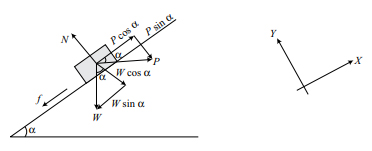
با استفاده از معادله‌های (۱) و (۲)‌ داریم:

$$P cos\alpha = W sin \alpha+ \mu (W cos \alpha + P sin\alpha) \\ = W sin \alpha + \mu Wcos \alpha + \mu P sin \alpha \\ Pcos\alpha - \mu P sin \alpha = Wsin \alpha+ \mu W cos \alpha \\ P = W \frac{sin \alpha + \mu cos \alpha}{cos\alpha- \mu cos \alpha}$$

اما به تعریف داریم:

$$\mu = tan\phi$$

با جایگذاری رابطه فوق در تساوی نیروی P داریم:

$$P = W \frac{sin \alpha + tan \phi \ cos \alpha}{cos\alpha- tan\phi \ cos \alpha}\\ = W \frac{sin \alpha cos \phi + sin \phi \ cos \alpha}{cos\alpha cos \phi- sin \alpha \ sin \phi } \\ =W\frac{sin (\alpha+\phi)}{cos (\alpha+ \phi)} \\ P = W tan (\alpha + \phi)$$

مثال فرمول اصطکاک برای نردبان

هنگامی که نردبانی را به دیوار تکیه می‌دهید، نیروی اصطکاک بین زمین و نردبان مانع از لغزیدن آن خواهد شد. در ادامه مثال‌هایی در مورد نیروی اصطکاک وارد شده بر نردبان حل می‌کنیم.

مثال اول فرمول اصطکاک برای نردبان

نردبان AB به طول L و وزن W به دیواری تکیه داده است. نیروهای $$R_A$$ و $$R_B$$ نیروهای عمودی سطح از طرف زمین و دیوار هستند. نردبان تمایل به لغزیدن بر روی زمین دارد. بنابراین، نیروهای $$f_A$$ و $$f_B$$ در خلاف جهت حرکت بر آن وارد می‌شوند. نمودار جسم آزاد را برای نردبان رسم کنید و شرایط تعادل را بنویسید.

پاسخ

نمودار جسم آزاد به صورت زیر برای نردبان رسم شده است.

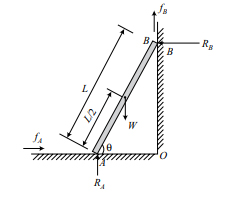
شرایط تعادل به صورت زیر برقرار هستند:

$$\sum F_x = 0 \ \Rightarrow \ f_A = R_B \\ \sum F_y = 0 \ \Rightarrow \ W = R_A + f_B$$

تعداد مجهول‌ها برابر چهار است. بنابراین، تعادل گشتاور حول نقطه O را نیز در نظر می‌گیریم:

$$\sum M_O = 0$$

مثال دوم فرمول اصطکاک برای نردبان

نردبان یکنواختی به وزن ۳۰۰ نیوتن به دیوار صافی تکیه داده و بر روی زمین زبری قرار گرفته است. اگر زاویه نردبان با سطح افقی برابر ۶۰ درجه باشد، نیروی اصطکاک بین زمین و نردبان را به دست آورید.

پاسخ

مثال اول حالت کلی‌تر مثال دوم است. بنابراین، از نمودار جسم آزاد مثال اول استفاده می‌کنیم. از آنجایی که دیوار صاف فرض شده است، نیروی اصطکاک آن برابر صفر خواهد بود:

$$f_B = 0$$

برای حالت تعادل داریم:

$$\sum F_x = 0 \ \Rightarrow \ f_A = R_B \ \Rightarrow \mu R_A = R_B \\ \sum F_y = 0 \ \Rightarrow \ R_A = W = 300 \ N \ \Rightarrow f_A = \mu R_A = 300 \mu$$

فرض کنید مقدار ضریب اصطکاک بین نردبان و زمین برابر ۰/۳ است. بنابراین، برای نیروی اصطکاک داریم:

$$f_A = 0.3 \times 300 = 90 \ N$$

مثال سوم فرمول اصطکاک برای نردبان

نردبان یکنواختی به طول ۱۰ متر و وزن ۲۰ نیوتن به دیوار صافی تکیه داده است. انتهای پایینی نردبان در فاصله ۸ سانتی‌متری از دیوار قرار گرفته است. در این حالت، نردبان در آستانه لغزش قرار می‌گیرد. مطلوب است تعیین:

1. ضریب اصطکاک بین نردبان و زمین.
2. نیروی اصطکاک وارد شده بر نردبان در نقطه تماس بین نردبان و زمین.

پاسخ

نمودار جسم آزاد نردبان به صورت زیر ترسیم شده است.

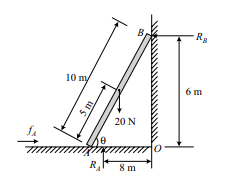
زاویه‌ای که نردبان با سطح افق ساخته است را به دست می‌آوریم:

$$cos\theta = \frac{8}{10}= 0.8 \\ \theta = 36.87^o \\ sin\theta = 0.6$$

شرایط تعادل به صورت زیر برقرار هستند:

$$\sum F_x = 0 \\ f_A = R_B \\ \sum F_y = 0 \\ R_A = W = 20 \ N \ (f_B = 0) \\ \sum M_O = 0 \\ R_A \times 8 = 20 \times 4 + R_B \times 6 \\ R_B \frac{R_A \times 8 -20 \times 4}{6 } = \frac{20 \times 8 - 20 \times 4 }{8 } = 10 \ N$$

مقدار نیروی اصطکاک عبارتست از:

$$f _A = R_b = 10 \ N\\ \mu = \frac{R_B}{N}= \frac{10}{20}= 0.5$$

سوالات چهارگزینه ای فرمول اصطکاک

در ادامه سوالاتی به صورت چهارگزینه‌ای حل خواهند شد.

مثال اول

جعبه‌ای به جرم M با سرعت v بر روی سطح صافی حرکت می‌کند. کوتاه‌ترین مسافت و زمانی که پس از آن جعبه به حالت سکون در می‌آید عبارتند از:

۱. $$\frac{v^2}{2\mu g}, \frac{v}{\mu g}$$

۲. $$\frac{v^2}{\mu g}, \frac{v}{\mu g}$$

۳. $$\frac{v^2}{2 M g}, \frac{v}{\mu g}$$

۴. هیچ‌کدام.

پاسخ

نیروی اصطکاک با حرکت جسم مخالفت می‌کند.

$$f = \mu N = \mu mg$$

بنابراین، شتاب کندشونده برابر است با:

$$a = \frac{F}{m} \ \Rightarrow \ a = \frac{\mu mg}{m} = \mu g$$

با استفاده از رابطه بین سرعت، مسافت طی شده و شتاب حرکت جسم داریم:

$$v^2=v_0^2+2a \triangle x$$

در نتیجه، کوتاه‌ترین مسافت طی شده توسط جسم قبل از توقف برابر است با:

$$x= \frac{v^2}{2\mu g}$$

همچنین، از رابطه بین سرعت، شتاب و زمان داریم:

$$v = v_0 + at \\ t = \frac{v}{\mu g}$$

مثال دوم

جسمی بر روی سطح شیب‌داری با زاویه $$\theta$$ می‌لغزد. ضریب اصطکاک با فاصله، y، به صورت $$\mu = Ky$$ تغییر می‌کند. در رابطه بیان شده K ثابت و y مسافت طی شده توسط جسم به سمت پایین است. نیروی کل وارد شده بر جسم در y=A برابر صفر است. مقدار K برابر است با:

۱. $$\frac{tan\theta}{A}$$

۲. $$Acot\theta$$

۳. $$\frac{cot\theta}{A}$$

۴. $$Atan\theta$$

پاسخ

نیروی $$mgsin \theta$$ به سمت پایین و نیروی $$\mu mgcos \theta$$ به سمت بالا بر جسم وارد می‌شوند. در نتیجه، نیروی خالص کل برابر است با:

$$f(y) = mg sin \theta - \mu mg cos\theta \\ = mg (sin \theta - Kycos \theta)$$

در y=A، $$f(y)$$ برابر صفر است. در نتیجه داریم:

$$0 = sin\theta - KA cos\theta \\ K = \frac{tan \theta}{A}$$

بنابراین، پاسخ صحیح گزینه یک است.

تاکنون با فرمول اصطکاک برای اصطکاک ایستایی و جنبشی آشنا شدیم و مثال‌هایی را در رابطه با این دو نوع اصطکاک حل کردیم. اما سوالی که ممکن است مطرح شود آن است که آیا می‌توان ضریب اصطکاک را اندازه گرفت؟ پاسخ به این سوال، بله است. در ادامه نشان می‌دهیم چگونه با طراحی آزمایشی ساده می‌توان ضریب اصطکاک را اندازه‌گیری کرد.

اندازه گیری ضریب اصطکاک

در ادامه با استفاده از آزمایشی ساده ضریب اصطکاک را اندازه می‌گیریم. همان‌گونه که گفته شد، اصطکاک نیرویی است که با حرکت آسان اجسام بر روی سطوح مخالفت می‌کند. در حالت کلی سه نوع نیروی اصطکاک وجود دارند:

1. اصطکاک خشک
2. اصطکاک سیال
3. اصطکاک داخلی

این آزمایش تنها برای اصطکاک خشک طراحی شده است. اصطکاک خشک نیز به دو نوع اصطکاک ایستایی و جنبشی تقسیم می‌شود. اندازه اصطکاک جنبشی کمتر از اصطکاک ایستایی است. در این مطلب با فرمول اصطکاک در حالت کلی و خاص آشنا شدیم. گفتیم، نیروی اصطکاک متناسب با نیروی عمودی سطح است و این تناسب با ضریبی به نام ضریب اصطکاک بیان می‌شود.

جسمی به وزن W بر روی سطح شیب‌داری با زاویه $$\theta$$ قرار دارد. هنگامی که جسم در آستانه لغزش قرار می‌گیرد، داریم:

$$\mu W cos \theta = W sin \theta \\ \mu = tan \theta$$

وسایل مورد نیاز آزمایش اندازه‌ گیری ضریب اصطکاک

وسایل مورد نیاز برای انجام این آزمایش عبارتند از:

• سطح شیب‌دار از جنس فولاد ضدزنگ با شیب متغیر.
• آویزی به وزن ۵ نیوتن.
• وزنه‌های متفاوت.
• قطعه‌های کوچکی از جنس آلومینیوم، برنج، پلاستیک و شیشه.

روند آزمایش

در قسمت اول آزمایش، ضریب اصطکاک ایستایی مواد مختلف به دست می‌آوریم. برای این قسمت از چهار نوع ماده مختلف استفاده می‌کنیم. در ابتدا صفحه فولادی را در وضعیت افقی می‌گذاریم. در ادامه، قطعه ساخته شده از مواد مختلف را در وسط صفحه قرار می‌دهیم. سپس نخی را به قطعه متصل می‌کنیم و آن را از روی قرقره‌ای عبور می‌دهیم. آویز ۵ نیوتنی را به انتهای دیگر نخ متصل می‌کنیم و شیب صفحه فولادی را افزایش می‌دهیم. در زاویه مشخصی، قطعه قرار داده شده بر روی صفحه فولادی شروع به حرکت خواهد کرد.

با اندازه‌گیری زاویه موردنظر، مقدار ضریب اصطکاک ایستایی را با استفاده از رابطه زیر به دست می‌آوریم:

$$\mu = tan\theta$$

در رابطه فوق، زاویه $$\theta$$ زاویه‌ای است که قطعه در آستانه حرکت قرار می‌گیرد. آزمایش را برای هر قطعه سه بار تکرار می‌کنیم و از مقدارهای به دست آمده برای ضریب اصطکاک ایستایی میانگین می‌گیریم.

قطعه آلومینیومی

زاویه $$\theta$$ برای قطعه آلومینیومی اندازه ‌می‌گیریم.

قطعه برنجی

زاویه $$\theta$$ برای قطعه از جنس برنج اندازه ‌می‌گیریم.

قطعه پلاستیکی

زاویه $$\theta$$ برای قطعه از جنس پلاستیک اندازه ‌می‌گیریم.

قطعه شیشه‌ ای

محاسبات و نتایج

با به دست آوردن زاویه $$\theta$$، ضریب اصطکاک ایستایی برای هر قطعه را به دست می‌آوریم:

برای آلومینیوم داریم:

$$\mu = tan (15.8) = 0.28$$

ضریب اصطکاک برای قطعه پلاستیکی برابر است با:

$$\mu = tan (20) = 0.36$$

برای قطعه از جنس برنج داریم:

$$\mu = tan (14) = 0.25$$

و برای قطعه شیشه‌ای داریم:

$$\mu = tan (18.8) = 0.34$$

معرفی فیلم آموزش فیزیک - پایه دوازدهم

مجموعه فرادرس در تولید و محتوای آموزشی خود اقدام به تهیه فیلم آموزش فیزیک - پایه دوازدهم برای دانش‌آموزان رشته‌های علوم‌تجربی و ریاضی‌فیزیک کرده که این مجموعه آموزشی از بیست‌وسه درس تشکیل شده است.

در درس‌های یکم تا چهارم مبحث حرکت بر خط راست را فرا خواهید گرفت. در درس‌های پنجم تا هشتم دینامیکِ حرکت دایره‌ای آموزش داده می‌شود. در درس ششم این مجموعه آموزشی با نیروی اصطکاک آشنا خواهید شد. در نتیجه، پس از تماشای این دوره آموزشی و خواندن این مطلب، با فرمول اصطکاک و نحوه استفاده از آن برای حل مسائل مختلف مربوط به اصطکاک ایستایی و جنبشی آشنا می‌شوید.

• برای دیدن فیلم آموزش فیزیک -پایه دوازدهم + اینجا کلیک کنید. 

جمع‌بندی

در این مطلب از مجله فرادرس، در مورد فرمول اصطکاک صحبت کردیم. در ابتدا، فرمول‌های اصطکاک برای دو نوع اصطکاک ایستایی و جنبشی بیان و در ادامه مثال‌هایی در مورد این دو نوع اصطکاک حل شدند. در پایان، آزمایش ساده‌ای برای به دست آوردن ضریب اصطکاک ایستایی و داشتن درک بهتری از مفهوم این ضریب، آموزش داده شد.