عدسی چیست؟ | تعریف، کاربرد، طرز کار و انواع – به زبان ساده
در این مطلب در مورد عدسی یا لنز و ویژگیهای آن صحبت میکنیم. در حقیقت عدسیها در پیشبرد علوم مختلف از جمله نجوم و ستاره شناسی نقش مهمی ایفا میکنند. بزرگنمایی این عناصر اپتیکی سبب شده است که اینک ما نسبت به جزئیات اجرام آسمانی دور در آسمان آگاه باشیم. در این مطلب به بررسی و مطالعه عدسیها و کاربردهای آنها در زندگی روزمره میپردازیم.


عدسی چیست؟
عدسی قطعهای از مواد شفاف است که به شکلی ساخته شده است که باعث میشود تابشهای نور هنگام عبور از آن به روشی خاص خم شوند. این خم شدن میتواند به این معنی باشد که تابشها در یک نقطه خاص همگرا میشوند و یا اینکه از یک نقطه خاص واگرا میشوند.
مواد مورد استفاده برای ساخت لنز میتواند یک تکه شیشه یا پلاستیک باشد و شکل لنز تعیین میکند که باعث همگرایی یا واگرایی پرتوهای نور میشود. کلمه لنز به دلیل شباهت شکل لنزهای همگرا و حبوبات از کلمه لاتین عدس نیز استفاده میکند و به آن لنز نیز گفته میشود.
خم شدن واقعی تابشهای نوری تولید شده توسط لنز به این دلیل اتفاق میافتد که ضریب شکست عدسی نسبت به هوای اطراف مقدار متفاوتی دارد. این رفتار توسط قانون اسنل برای شکست نور توصیف میشود که مربوط به زاویه متفاوت بین شعاع تابشی و نور شکسته شده با شاخصهای شکست برای دو ماده است.
به طور خلاصه این قانون میگوید اگر پرتو نوری از محیطی با ضریب شکست پایین تر به محیطی با ضریب شکست بالاتر (مثلاً از هوا به شیشه) برود، پرتوی نور به خط نرمال که عمود بر سطح است نزدیک میشود. همچنین عکس این موضوع در مورد پرتوهای نوری که از ماده با ضریب شکست بالاتر به ماده با ضریب شکست پایینتر میروند نیز صدق میکند.
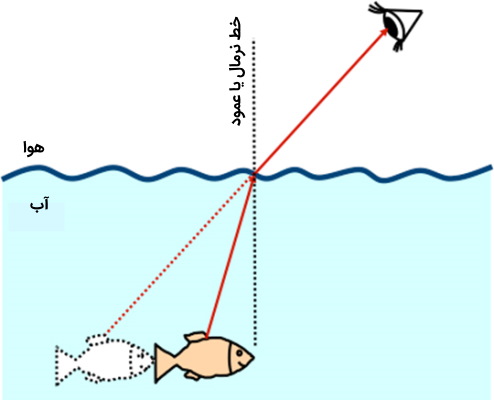
پارامترهای مهم در اپتیک تابش نوری
با این مقدمه باید گفت در اپتیک اصطلاحات منحصر به فردی به کار رفته است که در مطالعه فیزیک عدسیها به آنها برخورد خواهید کرد. به همین منظور و برای مطالعه عدسیها در ادامه این مفاهیم را توضیح میدهیم.
- «نقطه کانونی» (focal point)، نقطهای است که پرتوهای موازی پس از عبور از لنز به هم نزدیک میشوند.
- «فاصله کانونی» (focal length) لنزها فاصله مرکز لنز تا نقطه کانونی است که اساساً قدرت خمش لنز را تعریف میکند.
- «محور نوری» (optical axis)، خط تقارن عدسی است.
- «پرتوی نور» (light ray)، مسیر تقریبی حرکت پرتوی نوری است، جایی که از خطوط مستقیم برای نشان دادن حرکت امواج نور (یا فوتونها) استفاده می شود. هر نقطه روی یک جسم پرتوهای نور را در هر جهت تابش میکند، اما معمولاً چند پرتوی خاص برای تعیین محل تصویر حاصل انتخاب میشود.
- عدسی نوری یک قطعه از ماده است که به منظور همگرایی (لنز محدب) یا واگرایی (لنز مقعر) پرتوهای نور طراحی شده است.
- عدسی که از دو لنز محدب تشکیل شده است یک لنز نوری ساده با دو ضلع محدب است (شکلی مانند عدس دارد که نام لنز از آن گرفته شده است) و گاهی اوقات لنز محدب محدب نامیده میشود و فاصله کانونی آن مثبت است. از این عدسی در ذرهبین، تلسکوپ، میکروسکوپ و حتی چشم انسان استفاده میشود.
- عمق میدان، محدوده مسافتی را که در آن اشیا با فوکوس کردن عدسی از طریق لنز مشاهده میشوند را توصیف میکند و از اصطلاحات رایج در عکاسی است. از آنجا که سنسورهای نور در دوربینها اندازه ثابت دارند اگر تصویر کمی غیر فوکوس باشد اما میزان خطا به اندازه کافی کم باشد، در واقع این تصویر خارج از فوکوس ثبت نمیشود. بدین ترتیب دامنه فوکوس، عمق میدان نامیده میشود.
- لنز پرایم عدسی است که با فاصله کانونی ثابت در عکسبرداری استفاده میشود، این عدسیها در برابر لنزهای بزرگنمایی هستند که میتوان فاصله کانونی را در آنها تغییر داد. هر چند در زمینههای دیگر نیز میتوان از لنزهای پرایم به معنای لنزهای اولیه در سیستمی متشکل از چند لنز استفاده کرد.
نمودار تابش
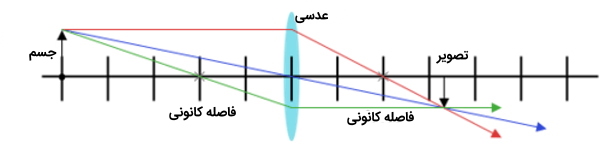
نمودارهای تابش ابزاری بسیار مفید در اپتیک هستند و از آنها برای یافتن مکانی که تصویر بر اساس موقعیت جسم و لنز تشکیل میشود، استفاده میشود. با کشیدن تعدادی پرتو نوری از شی و مشخص کردن مسیر این پرتوها و نحوه انحراف و خم شدگی این پرتوها، نقطهای که این پرتوها با یکدیگر برخورد میکنند، نقطهای است که در آن نقطه تصویر تشکیل میشود.
این فرآیند را میتوان با استفاده از قانون شکست اسنل نیز انجام داد، اما چند ترفند نیز میتواند روند کار را ساده کند. به عنوان مثال پرتویی که از وسط لنز عبور می کند به سختی منحرف میشود و پرتویی که به صورت عمودی با لنز برخورد میکند، به گونهای شکسته میشود تا از نقطه کانونی لنز عبور کند.
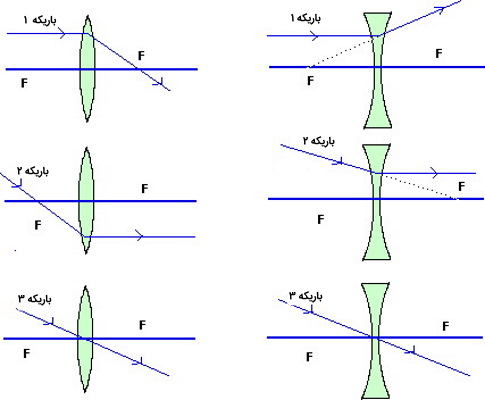
تصویر تولید شده توسط لنز میتواند حقیقی یا مجازی باشد. برای یک تصویر واقعی، پرتوهای نور همگرا میشوند و یک تصویر را در یک مکان خاص تشکیل میدهند و اگر صفحهای را در آن مکان قرار دهید، میتوانید آن تصویر را در چشم انسان و منطقه پشت لنز دوربین ببینید، شبکهها و مواد حساس به نور برای نمایش این تصویر مورد استفاده قرار میگیرند.
اما یک تصویر مجازی متفاوت است، وقتی پرتوها از عدسی جدا میشوند واگرا میشوند و جهت حرکت آنها باعث میشود که به نظر برسد این پرتوها از محل تصویر مجازی تابش میشوند. به عبارت دیگر اگر پرتوهای شکسته شده را به سمت عقب دنبال کنید و روی پرتوهای نوری حرکت کنید خواهید دید که همه آنها در محل تصویر مجازی جمع میشوند. با این حال پرتوهای نوری از نظر فیزیکی در این مکان جمع نمیشوند و اگر صفحهای را در این نقطه قرار دهید تصویری مشاهده نمیکنید.
عدسی همگرا چیست؟
عدسی همگرا که با نامهای دیگری مانند عدسی کوژ یا محدب نیز شناخته میشود، یک محیط شفاف منحنی ساخته شده از شیشه است که میتواند بخشی از یک کره جمع و جور باشد. سطح این لنز دارای یک منحنی خارجی یا برآمدگی است که مانند سطح یک گلوله شیشهای به نظر می رسد. وقتی پرتوهای نوری روی سطح محدب این لنز فرود میآیند، در مسیر خود همگرا میشوند.
وقتی هر دو سطح ماهیت محدب داشته باشند، به آنها عدسی بایکانوکس یا دو محدبی گفته میشود. وقتی یک سطح صاف باشد و سطح دیگر محدب باشد، به آن لنزهای محدب ساده یا پلانو کانوکس گفته میشود. رفتار لنزها به درجه انحنای لنزهای محدب بستگی دارد. وقتی پرتوهای موازی با سطح محدب این لنزها برخورد میکنند، تمایل به همگرایی و فوکوس در یک نقطه واحد دارند. به این نقطه، نقطه کانونی عدسی گفته میشود. فاصله کانونی برابر با فاصله بین نقطه کانونی و مرکز لنز است. نقطه کانونی را کانون اصلی عدسی نیز مینامند.
در این نوشتار، شما خواهید آموخت که چگونه موقعیت یک جسم در محور اصلی و فاصله آن از کانون عدسی، اندازه و نوع تصاویر تشکیل شده را تعیین میکند. از این لنز برای اهداف متفاوتی استفاده میشود که در ادامه آنها را بیان میکنیم. برای مطالعه بیشتر پیرامون عدسی محدب یا همگرا مطلب عدسی محدب (همگرا) — به زبان ساده (+ لینک مطلب) را مطالعه کنید.
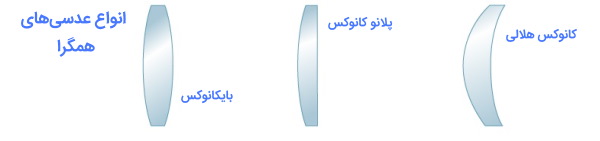
کاربردهای عدسی محدب
از عدسیهای محدب در میکروسکوپ، ذره بین و عینک استفاده میشود. همچنین این عدسیها در دوربینها برای ایجاد تصاویر واقعی از اشیا موجود در فاصله مشخص مورد استفاده قرار میگیرند. ماهیت تصاویر به نحوه استفاده از این لنزها بستگی دارد. دلیل اصلی یادگیری کاربردهای لنزهای محدب این است که دریابیم چگونه از شکست نور برای دیدن درست اجسام استفاده میشود.
مثال های کاربرد فوق در مورد لنز محدب بیانگر نحوه استفاده از این لنزها برای ایجاد تصاویر واقعی برای رسیدن به یک هدف است. در عینکها، لنزهای محدب یا همگرا به چشم نزدیکتر هستند تا بتوانند یک تصویر مجازی ایجاد کنند. در مورد تصاویر مجازی و حقیقی و تفاوت آنها در بخش قبل صحبت کردیم و در ادامه نیز آنها را بیشتر بررسی میکنیم.
عدسی واگرا چیست؟
عدسی واگرا، مقعر یا کاو نوعی محیط شفاف ساخته شده از شیشه است که دارای یک یا دو سطح مقعر است. بهترین راه برای تشخیص لنز مقعر بررسی سطح منحنی است. این سطح شبیه به سطح داخلی کره توخالی است. همان طور که گفتیم این لنزها، عدسی یا لنز واگرا نیز نامیده میشوند زیرا پرتوهای موازی روی سطح این عدسی تمایل دارند به صورت واگرا پراکنده شوند.
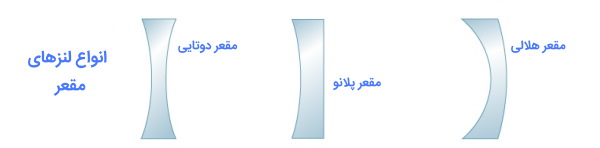
عدسیهای مقعر هرگز نمیتوانند یک تصویر واقعی تولید کنند زیرا خاصیت آنها این است که پرتوهای نور را از مسیر خود دور کنند. این موضوع بدان معنی است که پرتوهای نور از نظر فیزیکی در یک نقطه جمع نمیشوند و به هم نمیرسند. وقتی پرتوهای نوری را به صورت مجازی به سمت عقب ادامه دهیم یک نقطه تلاقی از پرتوها به وجود میآید. این تفاوت اصلی بین لنز مقعر و محدب است. اگر معادله فاصله کانونی و فاصله جسم را برای این لنز حل کنیم، متوجه میشویم که فاصله تصویر همیشه منفی است و این بدان معنی است که تصویر در طرف مقابل پرتوهای شکسته شکل میگیرد. برای آشنایی بیشتر با عدسی مقعر مطلب عدسی مقعر (واگرا) — به زبان ساده (+ لینک مطلب) را مطالعه کنید.
کاربردهای عدسی واگرا
از لنز مقعر برای واگرایی پرتوهای ورودی استفاده میشود. این موضوع به ایجاد یک تصویر مجازی در سمت مخالف سطح شکست کمک میکند. از این رو این عدسیها در دوربینهای شکاری، تلسکوپ، دوربین، چراغ قوه و عینک مورد استفاده قرار میگیرند. برخلاف تصاویر واقعی، تصاویر در این عدسیها به حالت ایستاده و قائم هستند. به این ترتیب میتوان با یادگیری ویژگیهای تابش نور در داخل لنزها، عدسی مقعر و محدب را تشخیص داد.
وقتی ساختار و ویژگیهای یک لنز مقعر و محدب را دنبال کنید، تفاوت فرمولها و روابط بین این دو عدسی را به وضوح درک خواهید کرد. در حقیقت رابطه بین فاصله کانونی، فاصله تصویر و فاصله جسم را میتوان با استفاده از ویژگیهای هر لنز تنظیم کرد.
تفاوت بین عدسی واگرا و همگرا چیست؟
از لحاظ ظاهری عدسی همگرا در مرکز ضخیمتر و در لبهها نازکتر است، در حالی که عدسی واگرا در مرکز نازکتر و در لبهها ضخیمتر است. عدسی همگرا پرتوهای نوری را همگرا و لنز واگرا این پرتوها رو واگرا میکند.
تصویر حاصل از عدسی همگرا واقعی و تصویر حاصل از عدسی واگرا مجازی است. تصویر در لنز همگرا وارونه است و در لنز واگرا مستقیم است. در جدول زیر این تفاوتها را به صورت لیست بیان کردهایم:
| کمیت | عدسی همگرا | عدسی واگرا |
| تعریف | این عدسی پرتوهای نوری را در یک نقطه در مسیر حرکت پرتوهای نوری همگرا کرده و با هم تلاقی میدهد. | این لنز پرتوهای نوری را پراکنده و واگرا میکند. |
| ساختار | این عدسی در میانه ضخیمتر و در لبهها نازکتر است. | این لنز در میانه نازک و در لبهها ضخیمتر است. |
| تشکیل تصویر | این لنز تصویر واقعی تشکیل میدهد ولی اگر جسم در وسط و بر روی مرکز اپتیکی باشد تصویر موهومی است. | تصویر عدسی واگرا مستقیم، مجازی و کوچکتر از جسم است. |
| انحنای عدسی | انحنای این عدسی به سمت خارج است. | انحنای این عدسی به سمت داخل است. |
| طول کانونی | طول کانونی مثبت است. | طول کانونی منفی است. |
| جسم | به دلیل ضخامت لنز در مرکز، جسم بزرگتر و نزدیکتر دیده میشود. | به دلیل نازک بودن عدسی در مرکز، جسم کوچکتر و دورتر دیده میشود. |
| باریکه نوری | باریکههای نوری بعد از عبور از این لنز همگرا میشوند و در یک نقطه فوکوس میشوند. | باریکههای نوری بعد از عبور از این عدسی پراکنده شده و در مسیرهای گوناگونی حرکت میکنند. |
| محل تصویر | تصویر و جسم هر دو در یک سمت لنز قرار دارند. | تصویر در یک سمت و جسم در سمت دیگر عدسی قرار دارد. |
| استفاده در زندگی واقعی | از عدسیهای محدب برای رفع مشکل دوربینی در عینکها استفاده میشود. | از لنزهای مقعر برای اصلاح مشکلات نزدیک بینی استفاده میشود. |
| ابزاری با استفاده از این لنزها | دوربین شکاری و تلسکوپ، دوربینهای عکاسی، عینک، چراغ قوه یا لیزرها (پخشکنندههای سی دی و دی وی دی) | به عنوان آینه بغل برای مسافر و رانندگان اتومبیل استفاده میشود. همچنین برای اهداف امنیتی در سوپرمارکتها و آپارتمانها استفاده میشود. برای ساخت لنزهای عینک آفتابی نیز از این عدسی استفاده میشود. |
نحوه عملکرد عدسیها
لنز دوربین یکی از آشناترین انواع لنزهایی است که روزانه با آن روبرو میشوید. لنزها در انواع مختلفی وجود دارند، اگرچه همه آنها از اصول اساسی عملکردی که قبلاً شرح داده شد پیروی میکنند.
لنز پرایم یک عدسی اصلی با فاصله کانونی ثابت و لنز زوم دارای یک فاصله کانونی متغیر است، بنابراین لازم نیست که مکان خود را به طور فیزیکی تغییر دهید تا بر روی چیزی یا جسمی فوکوس کنید. یک لنز با زاویه دید عریض، لنزی با فاصله کانونی بسیار کوچک است که به طور چشمگیری میدان دید را افزایش میدهد و لنز fisheye در اصل یک نسخه توسعه داده شده از لنزی با زاویه دید عریض است.
مثالهای دیگر، لنزهای تله فوتو هستند که فاصله کانونی آنها بسیار طولانی است و برای گرفتن سوژههایی که دور هستند استفاده میشوند. لنزهای ماکرو برای فوکوس در دامنههای بسیار نزدیک طراحی شدهاند و نسخههای بزرگ شده از اشیاء را تولید میکنند.
دیگر انواع رایج لنزها، لنزهای عینک یا لنز تماسی هستند و هر دوی این عدسیها یا لنزها برای رفع مشکلات بینایی شما استفاده میشوند. بدین ترتیب اگر شما نزدیک بین هستید، این موضوع بدان معنا است که لنزهای چشم شما در مقابل شبکیه حساس به نور در چشم شما تصاویر ایجاد میکنند و بنابراین شما برای حرکت دادن تصویر به عقب به عدسیهای واگرا (مقعر) نیاز دارید.
اگر چشمان شما دوربین باشد بدین معنی است که لنزهای چشمان شما تصویری فراتر از شبکیه شما ایجاد میکنند و بنابراین برای اصلاح این مسئله به عدسیهای همگرا نیاز دارید.
لنزهای تماسی و عینکها این موارد را به یک روش یعنی با اضافه کردن یک لنز اصلاحی اضافی برای ایجاد فاصله کانونی موثر چشم با فاصله شبکیه شما، اصلاح میکنند. اما در این میان تفاوتهایی وجود دارد زیرا لنزهای تماسی مستقیماً روی چشمان شما قرار میگیرند. در لنزهای تماسی، عدسیها نیازی به پوشاندن فضای بزرگی ندارند و فقط باید به اندازه کافی بزرگ باشند که مردمک چشم شما در حداکثر انداره خود را بپوشانند و میتواند با مواد کمتری به این مهم دست یابند. برای لنزهای عینک، لنزها باید منطقه بسیار بزرگتری را پوشش دهند و در نتیجه ضخیمتر هستند.
معادله عدسیها
برای یک لنز نازک و نزدیک به محور نوری آن، یعنی وقتی تقریب معتبر است، یک رابطه ساده بین فاصله جسم یعنی u (u فاصله بین جسم و لنز)، فاصله تصویر یعنی v (v فاصله بین تصویر کانونی و لنز) و فاصله کانونی لنز یعنی f وجود دارد. این معادله را میتوان با ملاحظات هندسی ساده به دست آورد.
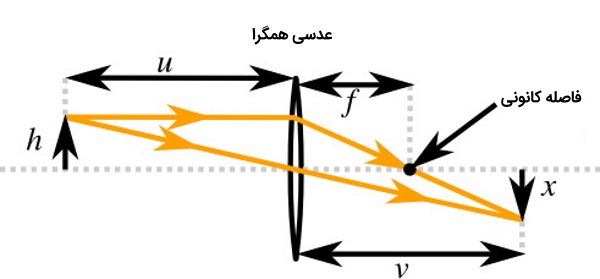
یک نقطه دلخواه روی جسم و یک لنز نازک همگرا را در نظر بگیرید. اگر جسم به اندازه کافی از لنز فاصله داشته باشد یک تصویر فوکوس شده در مکانی که پرتوها پس از عبور از لنز همگرا میشوند تولید میشود. البته با فرض این موضوع که لنز به شکلی ساخته شده است که چنین نقطهای وجود داشته باشد.
از بین پرتوهای بی نهایت زیادی که از جسم خارج میشوند، دو مورد به راحتی در نظر گرفته میشوند. اول پرتویی که به موازات محور نوری حرکت میکند پس از عبور از عدسی از فاصله کانونی گذر میکند.
در حالت دوم پرتویی را در نظر میگیریم که به سمت مرکز لنز هدایت میشود و از آنجا که لنز بسیار نازک است اساساً توسط لنز منحرف نمیشود. اگر h فاصله بین نقطه روی جسم و محور نوری و x فاصله بین تصویر نقطه و محور نوری باشد، با در نظر گرفتن مثلثهای مشابهی که در دو طرف تولید شده است داریم:
و همچنین داریم:
میتوان دید که با استفاده از معادله ابتدایی که نوشتیم میتوان بزرگنمایی لنز را محاسبه کرد و داریم:
با به دست آوردن نسبت از دو معادله بالا و برابر قرار دادن این دو نسبت با یکدیگر داریم:
اگر دو طرف معادله را بر تقسیم کنیم به معادله زیر دست مییابیم:
این معادله را در حالتی به دست آوردیم که جسم به اندازه کافی از یک عدسی نازک همگرا دور باشد، در این حالت پرتوهای نوری بعد از عبور از لنز همگرا میشوند و یک تصویر واقعی تشکیل میدهند. اما این معادله در حالت عمومیتر نیز برقرار است. در حقیقت اگر تصویر حقیقی را با علامت مثبت نمایش دهیم به دو بیان مهم زیر میرسیم:
- اگر تصویر واقعی (مجازی) تشکیل شود، برابر با علامت مثبت (منفی) فاصله بین تصویر و مرکز عدسی است.
- اگر جسم واقعی (مجازی) باشد، برابر با علامت مثبت (منفی) فاصله بین جسم و مرکز عدسی است.
ممکن است این سوال به ذهن شما خطور کند که یک جسم چگونه میتواند مجازی باشد. موقعیت زیر را در نظر بگیرید، یک عدسی واگرا را در نظر بگیرید که در برابر پرتوهای همگرا قبل از اینکه تصویر توسط این پرتوها تشکیل شود، قرار میگیرد. در این حالت عدسی واگرا در حقیقت یک تصویر حقیقی میسازد اما به عنوان یک جسم مجازی دیده میشود.
اگر جسم و تصویر هر دو در یک سمت محور نوری یا اپتیکی باشند (بالا یا پایین محور باشند)، تصویر به صورت قائم و تصویر دیگر یک تصویر وارونه است.
پرسش: جسمی در فاصله ۵ سانتیمتری از مرکز لنزی با فاصله کانونی قرار گرفته است. تصویر این جسم در چه فاصلهای از لنز ایجاد میشود؟ این تصویر حقیقی است یا مجازی؟
پاسخ: با استفاده از رابطه میتوان فاصله تصویر از لنز را به دست آورد و داریم:
بدین ترتیب تصویر در فاصله ۱۰ سانتی متری و به صورت مجازی تشکیل میشود.
توان عدسیها چیست؟
هر چه یک عدسی طول کانونی کوتاهتری داشته باشد، میتوان گفت عدسی قدرتمندتری است. توان یک عدسی برابر با عکس طول کانونی عدسی است و آن را برحسب دیوپتر اندازهگیری میکنند و با نمایش میدهند. در حقیقت داریم:
عدسی همگرا توان مثبت و عدسی واگرا توان منفی دارد.
معادله سازنده عدسی
فاصله کانونی یک عدسی نازک را که دو سطح آن تقریباً کروی و نزدیک به محور نوری است را میتوان با استفاده از معادله سازنده عدسی پیدا کرد. برای استخراج این معادله، دو پرتو که به عدسی میتابند را جداگانه در نظر میگیریم. در ادامه قرارداد و علامتهای مربوط به این مسائل را معرفی میکنیم.
فرض کنید یک پرتوی نور به قسمتی از یک سطح کروی که مرکز آن در C قرار دارد و شعاع آن R است برخورد میکند. شعاع این سطح کروی را اگر پرتوی نور از خارج سطح کروی وارد شود مثبت () و اگر این پرتوی نور از داخل سطح آمده باشد منفی () در نظر میگیریم.
بدین ترتیب اولین پرتو رسیده به صفحه کروی عدسی را با شعاع انحنای و مرکز در نظر میگیریم. در شکل زیر شعاع انحنای منحنی یعنی مثبت است و تصویری واقعی ارائه میدهد.
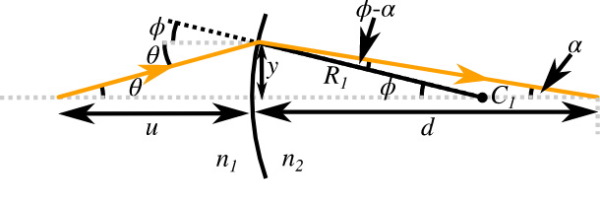
با استفاده از قانون اسنل میتوانیم رابطه بین زاویه ورودی یعنی و زاویه خروجی یعنی را به دست آوریم. با توجه به این که نزدیک به محور نوری هستیم میتوانیم فرض کنیم ، و و مجموع و تفاضلشان کوچک است و با در نظر گرفتن تقریب زاویه کوچک یعنی ، قانون اسنل به شکل زیر نوشته میشود:
با استفاده از طولهایی که در شکل بالا نشان داده شده است و تقریب زاویه کوچک، میتوان گفت ، و است. با قرار دادن این مقادیر در رابطه بالا، قانون اسنل به شکل زیر در میآید:
برای به دست آوردن اثر مرکب دو عدسی در اینجا تصویر حاصل از رابطه اول را به عنوان جسم برای عدسی دوم در نظر میگیریم. از آنجا که لنز نازک است و اصطلاحاً از تقریب لنز نازک یا تین لنز استفاده کردهایم، فاصله این تصویر (شی) میانی از لنز اول و دوم تقریباً برابر است.
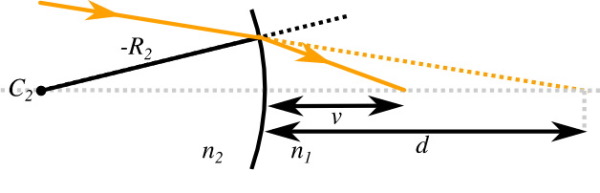
در شکل بالا، شعاع انحنای سطح دوم یعنی منفی است زیرا پرتو از داخل سطح منحنی حرکت میکند. با طولهایی که در شکل بالا نشان داده شده است و شباهت هندسی که بین دو شکل مورد بحث وجود دارد، خواهیم داشت:
با کم کردن معادله (**) از (*) داریم:
و از آنجا که ، معادله سازنده عدسی به شکل زیر به دست میآید:
اگر محیط ابتدایی هوا با ضریب شکست ۱ باشد (یعنی )، داریم:
ترکیب عدسی ها
برخلاف یک عدسی ساده که فقط از یک عنصر نوری یا یک عدسی تشکیل شده است، عدسیهای مرکب مجموعهای از عدسیهای ساده با یک محور مشترک هستند. استفاده از چندین عنصر امکان تصحیح انحرافات نوری بیشتری را فراهم میکند مانند انحرافات رنگی یا کروماتیک ناشی از شاخص شکست وابسته به طول موج در شیشه که تصحیح آن با استفاده از یک عدسی سخت است. در بسیاری از موارد این انحرافات با استفاده از ترکیبی از لنزهای ساده با انحرافاتی که تکمیل کننده یکدیگر هستند تا حد زیادی جبران میشود.

سادهترین حالت ترکیب عدسیها این است که این اجسام اپتیکی در تماس با یکدیگر قرار بگیرند. اگر فاصله کانونی این عدسیها و باشد و عدسیها نازک باشند، فاصله کانونی ترکیب این دو لنز برابر است با:
از آنجا که فاصله کانونی به نوعی توان عدسی است، میتوان دید که توان عدسیهایی که در تماس با یکدیگر هستند با یکدیگر جمع میشوند. اگر دو عدسی نازک توسط هوا از یکدیگر با فاصله d جدا شوند، به صورتی که d کوچکتر از فاصله کانونی هر یک از لنزها باشد، فاصله کانونی عدسی ترکیب شده در این حالت برابر است با:
اگر فاصله بین دو عدسی یعنی برابر با مجموع فاصله کانونی دو عدسی یعنی باشد، فاصله کانونی عدسی حاصل در بینهایت است.
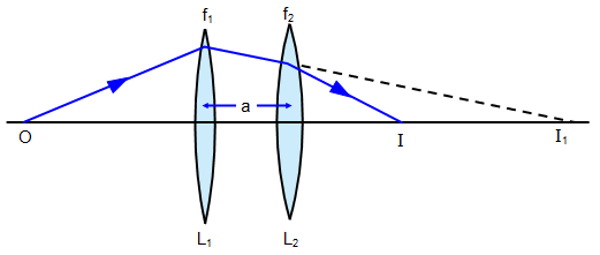
طول کانونی انتهایی
فاصله عدسی دوم تا نقطه کانونی عدسی ترکیبی را فاصله کانونی انتهایی یا BFL مینامند و داریم:
همانطور که d به سمت صفر میرود، مقدار کمیت BFL به مقدار f داده شده برای لنزهای نازک در تماس با یکدیگر متمایل میشود. اگر فاصله جدایی بین دو عدسی برابر با مجموع فاصله کانونی هر یک از عدسیها یعنی باشد، فاصله کانونی عدسی معادل و BFL بی نهایت میشوند.
این ترکیب مربوط به یک جفت عدسی است که پرتوهای موازی را به پرتوهای برخوردی تبدیل میکند و به چشم میرساند. به این نوع سیستم یک سیستم آفوکال (غیرکانونی) گفته میشود زیرا هیچ همگرایی یا واگرایی برای پرتوهای نوری ایجاد نمیکند. دو عدسی با فاصله از یکدیگر نوع سادهای از یک تلسکوپ نوری را تشکیل میدهند.
اگر چه این سیستم نمیتواند همگرایی یا واگرایی پرتوهای برخوردی را تغییر دهد، اما عرض باریکه را تغییر می دهد. بزرگنمایی این تلسکوپ توسط رابطه زیر داده میشود:
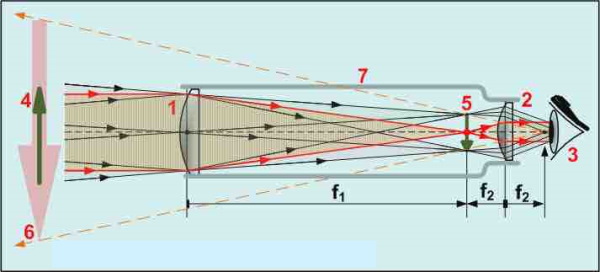
که برابر با نسبت بین عرض باریکه ورودی به خروجی است. دقت کنید که علامت قراردادی برای این حالت به شرح زیر است:
- تلسکوپی با دو عدسی محدبی یعنی و یک بزرگنمایی منفی ایجاد میکند که نمایش دهنده یک تصویر وارون است.
- یک عدسی محدب و یک عدسی یعنی ، یک تصویر با بزرگنمایی مثبت ایجاد میکند که نمایشدهنده یک تصویر مستقیم است.
آکروماتها چه هستند؟
لنز آکروماتیک یا آکرومات، لنزی است که برای محدود کردن اثرات انحراف یا ابیراهی رنگی و کروی طراحی شده است. لنزهای آکروماتیک طوری عمل میکنند تا دو طول موج (معمولاً قرمز و آبی یا بنفش) را در یک نقطه متمرکز کنند.
رایجترین نوع آکرومات، آکرومات دوتایی است که به طور معمول از دو عدسی جداگانه با شیشههایی که مقادیر مختلف پراکندگی دارند تشکیل شده است. یک عنصر این ترکیب دوتایی، یک عنصر منفی (مقعر) ساخته شده از بلور است که دارای پراکندگی نسبتاً بالایی است و عنصر دیگر، یک عنصر مثبت (محدب) ساخته شده از شیشه کراون است که پراکندگی کمتری دارد. عناصر عدسی در کنار یکدیگر نصب میشوند و غالباً به گونهای به یکدیگر چسبانده میشوند که ابیراهی رنگی یک عدسی توسط عدسی دیگر تصحیح شود.
در متداولترین نوع آکروماتها که در شکل زیر نشان داده شده است، توان مثبت عنصر عدسی کراون کاملاً با توان منفی عنصر عدسی بلور برابر نیست. این دو با هم یک عدسی مثبت ضعیف را تشکیل میدهند که دو طول موج مختلف نور را به یک کانون مشترک میرساند. دوتایی منفی که در آن توان عنصر منفی غالب است نیز برای برخی کاربردها ساخته میشود.
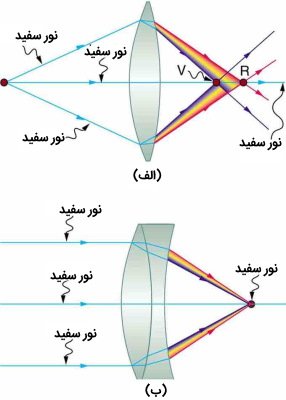
در تصویر ۱۱ (الف) انحراف رنگی به دلیل وابستگی شاخص شکست عدسی به رنگ (طول موج) ایجاد میشود. لنز برای رنگ بنفش (V) نسبت به رنگ قرمز (R) قدرت بیشتری دارد و تصاویر را با مکانها و بزرگنماییهای مختلف تولید میکند. ب) سیستمهای چند لنزی، مانند این آکروماتیک دوتایی میتوانند تا حدی انحراف رنگی را اصلاح کنند اما ممکن است به لنزهایی از مواد مختلف احتیاج داشته باشند و به هزینه سیستمهای نوری مانند دوربینها بیفزایند.
کار عدسی چیست؟
مهمترین کار لنزها فوکوس کردن یا متمرکز کردن نور در یک نقطه و تشکیل تصویر در آن نقطه است. بیشترین جایی که لنزها را دیدهاید در عینک افراد است.
منشور چیست؟
منشور یک جسم سه بعدی است که دو صفحه شبیه آن روبه روی هم قرار گرفتهاند. این صفحات مشابه روبه روی هم را پایه مینامیم. پایهها میتوانند مربع، مستطیل یا مثلث باشند. این وسیله دو کار اصلی انجام میدهد نور را پراکنده میکند یا جهت حرکت نور را اصلاح میکند. در بعضی موارد منشور بیش از یک عملکرد دارد.
یک منشور ساده مثلثی میتواند نور سفید را به نورهای تشکیل دهنده آن تجزیه کند که به آنها طیف میگوییم. هر یک از طیفها یا اجزای تشکیل دهنده نور سفید به مقدار متفاوتی منحرف میشوند. طیفهای با طول موج کوتاهتر (طیفهای به سمت نور بنفش در انتهای طیف) بیشترین مقدار خمیدگی را دارند و طیفهای با طول موج بلندتر (طیفهای به سمت قرمز در انتهای طیف) کمترین مقدار خمیدگی را نمایش میدهند.
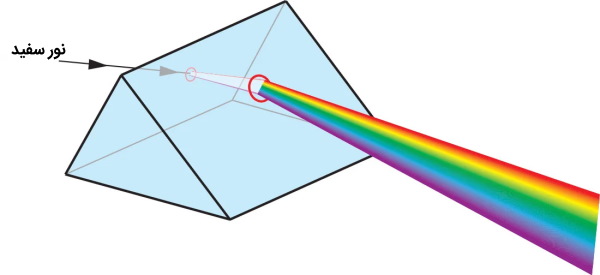
منشورها میتوانند جهت نور را با انعکاس داخلی معکوس کنند و به همین منظور در دوربینهای شکاری مورد استفاده قرار میگیرند. به نوعی میتوان گفت منشورها عکس عدسیها عمل میکنند و نور را پراکنده میکنند.
مثالهایی از مسائل عدسیها
پرسش: توان یک عدسی همگرا با فاصله کانونی ۲۵ سانتیمتر چه قدر است؟
پاسخ: فاصله کانونی را ابتدا به متر تبدیل میکنیم که این مقدار برابر با متر است. در نتیجه توان این عدسی برابر است با:
پرسش: توان یک لنز دیوپتر است. نوع لنز و فاصله کانونی آن چه قدر است؟
پاسخ: با توجه به رابطه بین توان و فاصله کانونی داریم:
در نتیجه طول کانونی این عدسی سانتیمتر و نوع لنز واگرا است.
پرسش: پزشکی یک عدسی با توان نسخه کرده است. فاصله کانونی این لنز چه قدر است؟ نوع لنز چیست و مشکل بینایی کسی که این نسخه برایش تجویز شده چیست؟
پاسخ: با توجه به اینکه توان این عدسی است و رابطه توان با طول کانونی عدسی داریم:
از آنجا که طول کانونی مثبت است، عدسی که نسخه شده است یک عدسی همگرا است. در نتیجه این نسخه برای فردی با مشکل دوربینی تجویز شده است.
پرسش: جسمی با طول ۵ سانتیمتر در فاصله ۲۵ سانتیمتری از یک عدسی همگرا با فاصله کانونی ۱۰ سانتیمتری قرار دارد. مکان، اندازه و نوع تصویر چگونه است؟
پاسخ: با توجه به اینکه ارتفاع جسم ۵ سانتیمتر است و جسم در فاصله ۲۵ سانتیمتری از یک عدسی همگرا قرار گرفته است و داریم سانتیمتر. فاصله کانونی عدسی نیز طبق دادههای مسئله ۱۰ سانتی متر است. با استفاده از رابطه لنزها داریم:
در نتیجه تصویر در فاصله ۱۶٫۷ سانتیمتری از عدسی تشکیل میشود. از طرفی از رابطه بزرگنمایی عدسی میدانیم:
با قرار دادن این مقادیر در رابطه ارتفاع تصویر برابر با سانتیمتر است. علامت منفی نشان دهنده این است که تصویر به صورت وارونه مشاهده میشود.
پرسش: سه لنز با توان ۲، ۲٫۵ و ۱٫۷ دیوپتر پشت سر هم قرار گرفتهاند. توان لنز ترکیبی این سه عدسی یا لنز چه قدر است؟
پاسخ: در این حالت توان عدسی ترکیبی این لنزها برابر است با:
پرسش: یک جسم در فاصله ۶۰ سانتیمتری یک تصویر موهومی در جلوی عدسی و در فاصله ۲۰ سانتیمتری تشکیل میدهد. طول کانونی این عدسی چه قدر است؟
پاسخ: با توجه به اینکه فاصله جسم یعنی برابر با ۶۰ سانتیمتر است و فاصله تصویر موهومی ۲۰ سانتیمتر است، فاصله کانونی با استفاده از رابطه لنز برابر است با:
پرسش: در شکل زیر یک عدسی همگرا با فاصله کانونی دو واحد داریم. همچنین جسمی از مرکز عدسی در فاصله ۵ واحد قرار گرفته است. الف) با رسم پرتوهای وارد شده بر عدسی مکان تقریبی جسم را روی شکل مشخص کنید. ب) نوع تصویر را مشخص کنید. ج) مکان تصویر را مشخص کنید.
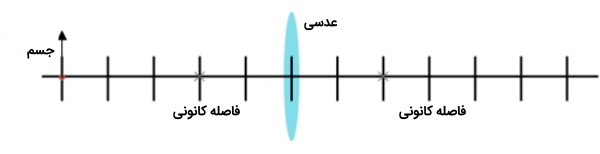
پاسخ: برای رسم محل تصویر در شکل سه پرتو را در نظر میگیریم:
- پرتویی که به مرکز عدسی میتابد و بدون آن مه منحرف شود به مسیر خود ادامه میدهد.
- پرتویی که از فاصله کانونی عدسی عبور میکند و در این حالت بعد از عبور از عدسی به صورت موازی با محور نوری ادامه مسیر میدهد.
- پرتویی که موازی با محور نوری به عدسی میتابد و در نتیجه باید بعد از عدسی به گونهای دچار شکست شود که از نقطه کانونی عدسی عبور کند.
با توجه به سه مورد بالا تصویر به شکل زیر تشکیل میشود.
ب) با توجه به تصویر ایجاد شده در شکل بالا باید گفت تصویر حقیقی و وارونه است.
ج) برای محاسبه محل تصویر از زابطه عدسی استفاده میکنیم و داریم:
رابطه بین عدسیها به شکل دیگر
در برخی از منابع فیزیک رابطه عدسی به این شکل نوشته شده است:
و در این حالت بزرگنمایی عدسی برابر با است. باید تاکید کنیم که برای بزرگنمایی عدسی سه حالت زیر را باید معرفی کرد:
- اگر بزرگتر از ۱ باشد جسم دچار بزرگنمایی شده است.
- اگر کوچکتر از ۱ باشد جسم کوچک شده است.
- اگر برابر با ۱ باشد جسم و تصویر اندازه یکسان دارند.
در جدول زیر علامتهای قراردادی برای پارامترهای مختلف در استفاده از معادله لنز با علامت منفی را معرفی میکنیم:
| نوع لنز | عدسی واگرا | عدسی همگرا |
| فاصله جسم تا لنز | با علامت منفی در رابطه قرار میگیرد. | با علامت منفی در رابطه قرار میگیرد. |
| فاصله تصویر تا عدسی | علامت آن منفی است چوت تصویر موهومی است. | میتواند مثبت یا منفی باشد. |
| بزرگنمایی | علامت آن مثبت است یعنی تصویر نسبت به جسم در حالت مستقیم است. | میتواند مثبت یا منفی باشد که به این معنی است که تصویر میتواند نسبت به جسم مستقیم یا وارونه قرار گیرد. |
| مقدار بزرگنمایی | همواره کوچکتر از یک است. | میتواند بزرگتر، کوچکتر با برابر با ۱ باشد. |
جواب نهایی در استفاده از رابطه عدسی چه با علامت مثبت و چه علامت منفی یکسان است.
جمع بندی
در این مطلب در مورد عدسی و ویژگیهای آن صحبت کردیم. به صورت کلی دو نوع عدسی همگرا و واگرا را معرفی کردیم و کاربردها و روابط حاکم بر این عدسیها را بیان کردیم. همچنین در مورد تفاوت این عدسیها و منشور نیز صحبت کردیم.
آزمون عدسی
۱. عدسی از نظر علمی چیست و عامل اصلی شکست نور در آن کدام است؟
عدسی تکهای شفاف است که اختلاف ضریب شکست باعث خم شدن نور میشود.
عدسی وسیلهای از فلز است که جهت نور را تغییر میدهد.
عدسی شفاف است و انحنای سطح تنها عامل شکست نور محسوب میشود.
عدسی جسمی مات با قابلیت جذب تمام نور است و شکست رخ نمیدهد.
در تعریف علمی، عدسی تکهای شفاف است (معمولا از شیشه یا پلاستیک) که پرتوهای نور را به دلیل اختلاف ضریب شکست بین لنز و محیط اطراف خم میکند.
۲. قانون اسنل چه اثری بر مسیر پرتوهای نور هنگام عبور از عدسی دارد؟
مسیر نور را فقط در عدسیهای واگرا تغییر میدهد.
باعث خم شدن نور در مرز بین دو محیط با ضریب شکست متفاوت میشود.
پرتوهای نور را بدون تغییر مسیر مستقیم عبور میدهد.
تمام نور تابیده شده را جذب و از انتشار آن جلوگیری میکند.
قانون اسنل توضیح میدهد که هنگام ورود نور به عدسی، اگر ضریب شکست عدسی با محیط تفاوت داشته باشد، مسیر نور خم میشود. این تغییر به علت اختلاف ضریب شکست رخ میدهد و نقش کلیدی در همگرایی یا واگرایی پرتوهای عبوری از عدسی دارد.
۳. نقطه کانونی عدسی چیست و چگونه تعیین میشود؟
محل قرارگیری عدسی نسبت به منبع نور
محل برخورد تمامی پرتوهای عبوری از مرکز عدسی
نقطهای که پرتوهای موازی پس از عبور از عدسی به آن جمع میشوند.
جایی که جسم شفافترین تصویر را ایجاد میکند.
عبارت «نقطهای که پرتوهای موازی پس از عبور از عدسی به آن جمع میشوند» تعریف دقیق نقطه کانونی یک عدسی است. این نکته در توضیحات عملکرد عدسی همگرا آمده که پرتوهای نور موازی ورودی پس از عبور از عدسی، در یک نقطه مشترک به نام کانون به هم میرسند.
۴. از نظر ساختار فیزیکی، چه تفاوتی بین عدسی محدب و عدسی مقعر وجود دارد؟
عدسی مقعر معمولا از پلاستیک شفاف ساخته میشود.
عدسی محدب در مرکز ضخیمتر و لبهها نازکتر است.
عدسی مقعر هر دو سطح تخت و بدون خمیدگی دارد.
عدسی محدب در مرکز نازک و لبهها ضخیم است.
در ساختار فیزیکی عدسی محدب، بخش مرکزی ضخیمتر از لبهها ساخته میشود و این تفاوت ساختار باعث همگرایی نور میگردد. برخلاف آن، عدسی مقعر در وسط نازکتر و لبهها ضخیمتر است.
۵. کدام ویژگی اپتیکی عدسی محدب باعث کاربرد آن در ابزارهایی مانند میکروسکوپ و تلسکوپ شده است؟
توانایی ایجاد تنها تصویر مجازی مستقیم از اجسام
قابلیت همگرایی پرتوهای نور و بزرگنمایی تصویر
امکان ارسال مستقیم نور بدون انحراف مسیر
افزایش ضریب شکست نسبت به عدسی مقعر
ویژگی «قابلیت همگرایی پرتوهای نور و بزرگنمایی تصویر» باعث میشود عدسی محدب برای ساخت ابزارهایی مانند میکروسکوپ و تلسکوپ مناسب باشد، زیرا این عدسیها پرتوهای نور را در یک نقطه جمع و تصویر واضح بزرگ ایجاد میکنند. «امکان ارسال مستقیم نور بدون انحراف مسیر» به عملکرد عدسی مربوط نیست و عدسی دقیقا مسیر پرتوها را خم میکند. «توانایی ایجاد تنها تصویر مجازی مستقیم از اجسام» برخلاف عدسی محدب است، زیرا عدسی محدب هم تصویر واقعی و هم مجازی میسازد بسته به محل جسم. «افزایش ضریب شکست نسبت به عدسی مقعر» ویژگی بارز و تعیینکنندهای برای کاربرد ابزارهای بزرگنمایی نیست.
۶. در رابطه ریاضی که به معادله عدسی معروف است، منظور از هر کدام از پارامترهای u، v و f چیست و این معادله معمولا برای حل چه نوع مسائلی بهکار میرود؟
u انرژی فوتون، v ضریب شکست، f شعاع کانونی است و برای ترکیب عدسیها استفاده میشود.
u فاصله جسم، v فاصله تصویر، f فاصله کانونی عدسی است و این معادله برای تعیین مکان تصویر و نوع آن در عدسیها کاربرد دارد.
u فاصله نور منبع، v زاویه تابش، f توان عدسی است و مخصوص تحلیل توزیع نور است.
u مقدار ضریب شکست، v شعاع انحنا، f فاصله نوری است و برای محاسبه توان بزرگنمایی بهکار میرود.
در معادله عدسی، u نمایانگر فاصله جسم تا عدسی، v فاصله تصویر تا عدسی و f فاصله کانونی لنز است. این معادله برای پیدا کردن محل و نوع تصویر در عدسیها، یعنی بررسی اینکه تصویر حقیقی یا مجازی و در چه فاصلهای تشکیل میشود، بهکار میرود.
۷. کدام جمله ارتباط توان عدسی با نوع عدسی را به درستی بیان میکند؟
عدسی با توان منفی همگرا است.
عدسی با توان منفی دو نوع تصویر میدهد.
عدسی با توان مثبت همگرا است.
عدسی با توان مثبت واگرا است.
براساس رابطه توان عدسی، اگر مقدار توان مثبت باشد، عدسی همگرا (محدب) است و پرتوها را جمع میکند. در مقابل، توان منفی نشانگر عدسی واگرا (مقعر) است که پرتوهای نور را واگرا میکند.
۸. برای اصلاح مشکل نزدیکبینی، چه عدسیای باید در عینک استفاده شود و دلیل آن چیست؟
عدسی آکروماتیک برای کاهش ابیراهی رنگی
عدسی مقعر برای واگرا کردن پرتوهای نور
عدسی محدب برای همگرا کردن پرتوها
عدسی پلانوکانوکس برای ایجاد تصویر بزرگ
در مشکل نزدیکبینی، پرتوهای نور پیش از رسیدن به شبکیه همگرا میشوند. «عدسی مقعر» (واگرا) با واگرا کردن پرتوهای ورودی، آنها را به عقب میبرد تا تصویر روی شبکیه تشکیل شود و فرد بتواند دور را واضح ببیند.
۹. بر اساس ویژگیهای عدسی همگرا و واگرا، چگونه نوع تصویر (واقعی یا مجازی) توسط هر یک ساخته میشود؟
عدسی همگرا فقط تصویر مجازی تولید میکند و عدسی واگرا تصویر واقعی میسازد.
عدسی همگرا میتواند تصویر واقعی و مجازی بسازد ولی عدسی واگرا فقط تصویر مجازی تولید میکند.
هر دو عدسی همگرا و واگرا فقط تصویر واقعی ایجاد میکنند.
هر دو عدسی همگرا و واگرا فقط تصویر مجازی میسازند.
عدسی همگرا (محدب) میتواند بسته به محل قرارگیری شیء نسبت به عدسی، هم تصویر واقعی و هم تصویر مجازی بسازد؛ اما عدسی واگرا (مقعر) همیشه پرتوهای نور را واگرا میکند و فقط تصویر مجازی تولید میکند.
۱۰. برای به دست آوردن فاصله کانونی کل یک سیستم اپتیکی که از دو عدسی با فاصله کانونیهای مختلف به طور متوالی و نزدیک به هم تشکیل شده، کدام روش درست است؟
میانگین ساده فاصلههای کانونی دو عدسی برابر با فاصله کانونی کل است.
جمع معکوس فاصلههای کانونی هر دو عدسی و سپس معکوس گرفتن حاصل، فاصله کانونی کل را میدهد.
جمع مستقیم فاصلههای کانونی هر دو عدسی فاصله کانونی کل را به دست میدهد.
تفریق فاصله کانونی اول از دومی برای محاسبه فاصله کانونی کل کافی است.
در سیستم اپتیکی که دو عدسی با فاصله کم کنار هم قرار داشته باشند، ابتدا باید معکوس فاصله کانونی هر عدسی (یعنی توان هر عدسی که برابر ۱ تقسیم بر f است) را با هم جمع کرد و سپس از مجموع آنها معکوس گرفت تا فاصله کانونی کل به دست آید. روش «جمع معکوس فاصلههای کانونی و سپس معکوس گرفتن حاصل» تنها راه صحیح جمعبندی توان عدسیهاست. جمع ساده فاصلهها، تفریق آنها یا گرفتن میانگین پاسخ درستی نمیدهد، چون رفتار عدسیها در ترکیب بر اساس جمع توان است نه خود فاصله کانونی. این اصل در ترکیب لنزها به طور مستقیم توضیح داده شده است.
۱۱. دیاگرام پرتو در عدسیهای همگرا و واگرا چه کمکی به تعیین نوع و محل تصویر میکند؟
تنها ضخامت عدسی را مشخص کرده و تصویری از نوع آن ارائه نمیدهد.
با مسیر پرتوهای کلیدی میتوان فهمید تصویر واقعی یا مجازی است و دقیقا کجا تشکیل میشود.
فقط تفاوت بین مواد سازنده عدسی را نشان میدهد و اثری بر تحلیل تصویر ندارد.
صرفا برای تعیین قدرت عدسی در بزرگنمایی استفاده میشود و مکان تصویر را نشان نمیدهد.
اگر با استفاده از دیاگرام پرتو مسیر چند پرتو کلیدی را رسم کنیم، میتوانیم دقیقا محل برخورد پرتوها در عدسی همگرا یا مسیر واگرای پرتوها در عدسی واگرا را مشاهده کنیم. این کار اجازه میدهد نوع تصویر (مثلا «تصویر واقعی یا مجازی») و موقعیت دقیق آن نسبت به عدسی را تعیین کنیم.
۱۲. استفاده از شیشههای مختلف در ساخت دابل آکرومات چه اثری در کاهش ابیراهی رنگی دارد؟
باعث تمرکز نور فقط در یک طول موج خاص میشود.
امکان متحد کردن نقاط کانونی دو طول موج مختلف را فراهم میکند.
موجب افزایش خطای رنگی عدسی نسبت به لنز ساده میشود.
صرفا شدت نور عبوری را افزایش میدهد.
با ترکیب دو نوع شیشه با پراکندگی متفاوت در دابل آکرومات نقاط کانونی مربوط به دو طول موج نور به یکدیگر نزدیک میشوند و ابیراهی رنگی تا حد زیادی رفع میشود.












