عدسی محدب (همگرا) – به زبان ساده

آیا تا به حال در مورد چگونگی تشکیل تصویر در عینک همکلاسی خود فکر کرده‌اید؟ به عملکرد میکروسکوپ‌ و یا تلسکوپ‌ها چطور؟ به احتمال خیلی زیاد در دوران کودکی با ذوق فراوان ذره‌بین در دست گرفته و دنیای اطرافتان را با آن تماشا می‌کردید. اگر تا‌کنون به چرایی و چگونگی تشکیل تصویر در ذره‌بین و یا عینک و یا حتی لنز دوربین‌های عکاسی فکر نکرده‌اید، با ما در ادامه این مقاله همراه شوید تا به زبانی ساده ساختار عدسی محدب (همگرا) یا همان «لنز محدب» (Convex Lens) را بررسی کنیم.

در مقالات پیشین فرادرس با اصول تشکیل تصویر در آینه‌های تخت، مقعر و محدب آشنا شدیم. عدسی یا لنزها نیز طبق قوانین بازتاب و شکست نور کار می‌کنند. عدسی‌ها شفاف بوده و از دو قسمت تشکیل شده‌‌اند. تشکیل تصویر در عدسی‌ها همانند آینه‌ها می‌تواند بر دو نوع حقیقی یا مجاری باشد. در این مقاله قصد داریم به طور خاص به عدسی «همگرا» (Converging) بپردازیم.

خصوصیات کلی عدسی محدب

یک عدسی محدب (همگرا) شکلی به فرم زیر دارد. در این نوع عدسی، وسط آن پهن‌تر از اطراف بوده و بسته به کاربردش به شکل‌های متفاوتی نظیر دو کوژ (دو طرف محدب)، تخت - کوژ، هلالی همگرا ساخته می‌شود.

اگر دسته‌ای نور به طور موازی به یک عدسی همگرا بتابد، پس از شکست توسط عدسی به یکدیگر نزدیک می‌شوند. دلیل انتخاب نام همگرا برای این نوع عدسی نیز همین امر است. پر استفاده‌ترین عدسی همگرا، نوع دو کوژ (دو طرف محدب) آن است که در این مقاله به آن می‌پردازیم. گفتیم که عدسی‌ها از دو قسمت تشکیل شده‌اند.

در واقع می‌توان گفت هر وجه از یک عدسی همگرا متعلق یه یک کره است (شکل ۲). پس یک عدسی همگرا دو نقطه (فاصله) کانونی و دو مرکز انحنا دارد. البته این امر برای عدسی‌های واگرا (دو طرف مقعر - دو کار) نیز صادق است.

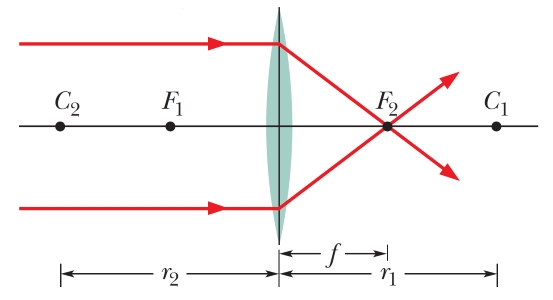
با توجه به شکل (2)، اصطلاحات زیر را تعریف می‌کنیم:

• محور اصلی عدسی: محوری است که از دو مرکز انحنای $$C_{1}$$ و $$C_{2}$$ می‌گذرد. تعریف مرکز انحنا در عدسی‌ها نیز به صورت تعریف مرکز انحنا در آینه‌های کروی است.
• مرکز نوری عدسی: نقطه‌ای است دقیقاً در مرکز عدسی. در واقع تلاقی محور اصلی عدسی و محوری که عدسی دو کوژ (دو طرف محدب) را از وسط به دو نیم تقسیم می‌کند، مرکز نوری عدسی است.
• کانون عدسی: اگر دسته‌ای پرتو نوری، موازی با محور اصلی به عدسی دو کوژ بتابند، در نقطه‌ای موسوم به نقطه کانونی همگرا می‌شوند (شکل ۲).
• فاصله کانونی: به فاصله بین کانون عدسی و مرکز نوری عدسی، فاصله کانونی می‌گویند.

توجه داشته باشید که مطابق شکل (۳) پرتو نور در یک عدسی دوبار شکست پیدا می‌کند. در واقع یک بار به هنگام ورود از هوا با ضریب شکست تقریباً ۱ به عدسی با ضریب شکست مشخص $$n$$ و یک بار به هنگام خروج از عدسی به هوا دچار شکست می‌شود.

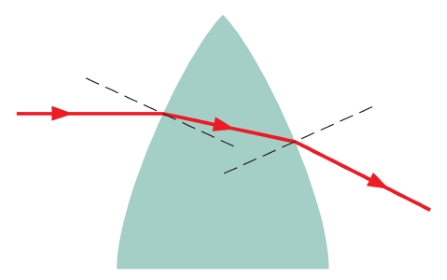
اکثرا مراجع برای ساده‌سازی تصاویر این اصل را رعایت نمی‌کنند و شکست نور در عدسی همگرا دو کوژ را مطابق بخش زیر در نظر می‌گیرند.

شکست پرتو در عدسی همگرای دو کوژ

با توجه به شکل (۴)، می‌توان ۳ اصل کلی زیر را در خصوص چگونگی شکست نور در عدسی همگرا دو کوژ عنوان کرد.

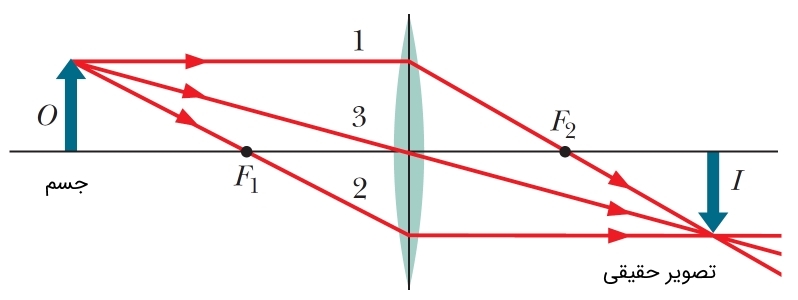
• اگر پرتویی موازی با محور اصلی به عدسی همگرا (محدب) بتابد، پس از شکست از نقطه کانونی می‌گذرد (پرتو ۱).
• اگر پرتویی چنان بتابد که از نقطه کانونی  گذر کند، پس از شکست، موازی با محور اصلی خارج می‌شود (پرتو ۲).
• اگر پرتویی به مرکز نوری عدسی بتابد، بدون شکست در همان مسیر از عدسی خارج می‌شود (پرتو ۳).

با توجه به سه نکته فوق، دو نوع تصویر حقیقی و مجازی می‌تواند توسط یک عدسی دو کوژ حاصل شود. در خصوص تلاقی امتداد پرتوهایی که توسط عدسی شکست پیدا می‌کنند، طبق شکل (۵) تصویر جسم به صورت مجازی تشکیل می‌شود.

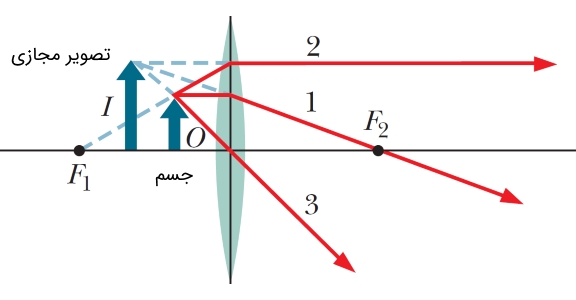
چگونگی تشکیل تصویر در عدسی همگرای دو کوژ

به دست آوردن مکان و حالت تصویر در عدسی همگرا دو کوژ اصلاً کار دشواری نیست. برای این امر، تنها به کارگیری ۳ اصلی که در بخش قبل عنوان شد کفایت می‌کند. اگر تصویر از تلاقی پرتوهای خارج شده از عدسی تشکیل شد، تصویر را حقیقی (همانند شکل ۴) و اگر از امتداد پرتوهای خارج شده از عدسی تشکیل شود (همانند شکل ۵)، تصویر را مجازی می‌نامیم.

برای عدسی همگرا دو کوژ یا به اختصار عدسی محدب، که دو فاصله کانونی آن برابر هستند، تمامی حالت‌های مختلف تشکیل تصویر در ادامه لیست شده‌اند. در شکل‌های زیر $$AB$$ طول جسم و $$A'B'$$ طول تصویر هستند.

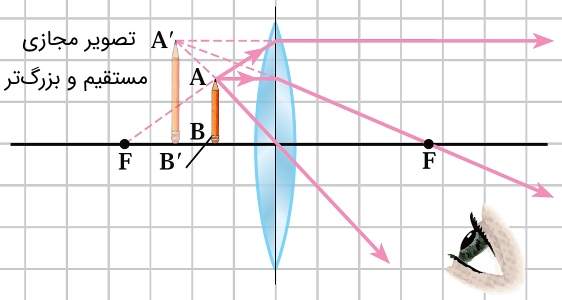
جسم در فاصله کانونی عدسی (بین عدسی و نقطه $$F$$):  در این حالت پرتوهای شکسته شده توسط عدسی از هم دور می‌شوند، در نتیجه از تلاقی امتداد آن‌ها تصویری مجازی، بزرگ‌تر و مستقیم با جسم حاصل می‌شود.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

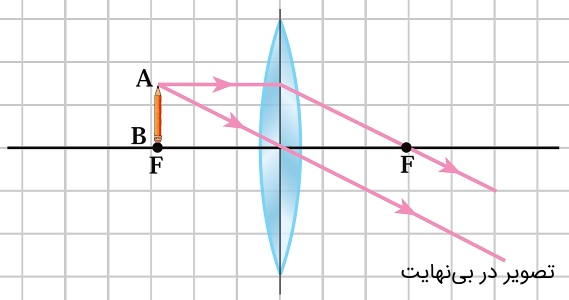
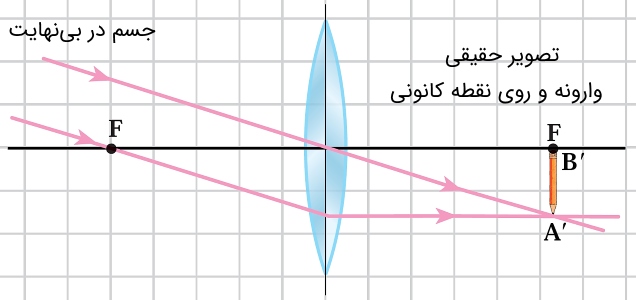
جسم روی نقطه کانونی $$F$$: پرتوهای شکسته شده به صورت موازی از عدسی خارج شده و به اصطلاح تصویر در بی‌نهایت تشکیل می‌شود.

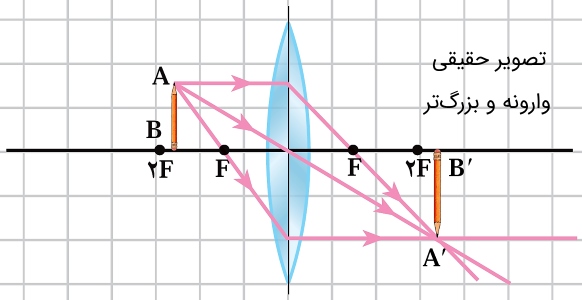
جسم بین نقطه کانونی $$F$$ و نقطه $$2F$$: تلاقی پرتوهای شکسته و خارج شده از عدسی در نقطه‌ای بیشتر از فاصله $$2F$$ به صورت حقیقی، وارونه و بزرگ‌تر از جسم تشکیل می‌شود.

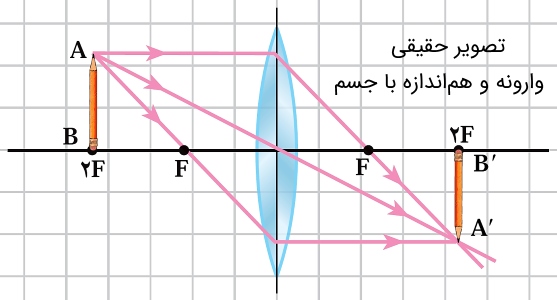
جسم روی نقطه $$2F$$: تلاقی پرتوهای شکسته و خارج شده از عدسی در نقطه‌ $$2F$$ به صورت حقیقی، وارونه و هم‌اندازه با جسم تشکیل می‌شود.

جسم خارج از فاصله $$2F$$: تلاقی پرتوهای شکسته و خارج شده از عدسی در نقطه‌ای بین $$F$$ و $$2F$$ به صورت حقیقی، وارونه و کوچک‌تر جسم تشکیل می‌شود.

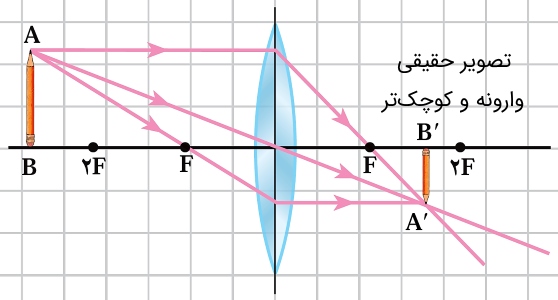
جسم در بی‌نهایت: تلاقی پرتوهای شکسته و خارج شده از عدسی در نقطه‌ $$F$$ به صورت حقیقی، وارونه تشکیل می‌شود.

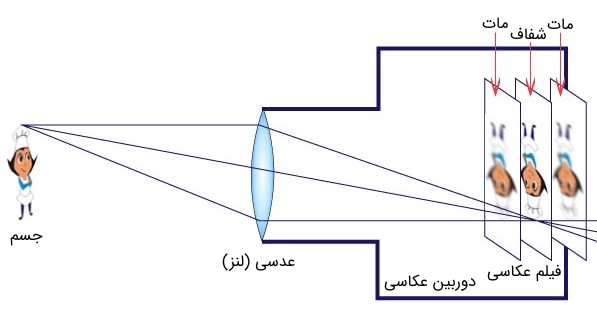
با توجه به مطالب فوق، حال مشخص است که چرا با تغییر در مکان یک لنز دوربین عکاسی تصویر در نقطه‌ای شفاف و در نقاط دیگر مات است (شکل ۶).

معادله عدسی

در جدول فوق دیدیم که مکان و حالت تصویر بستگی به موقعیت مکانی جسم نسبت به نقطه‌کانونی $$F$$ دارد. معادله‌ای که ارتباط بین موقعیت جسم و تصویر را نسبت به فاصله کانونی در عدسی‌ها مشخص می‌کند (البته عدسی‌‌های نازک) همانند معادله اصلی آینه‌های کروی است و به همان روش به دست می‌آید. این معادله به فرم آشنای زیر است:

$$\frac{1}{p}+\frac{1}{q}=\frac{1}{f}$$

در رابطه فوق $$f$$ فاصله کانونی، $$p$$ فاصله جسم تا مرکز نوری عدسی و $$q$$ فاصله تصویر تا مرکز نور عدسی است.

همچنین رابطه زیر را می‌توان برای فاصله کانونی «عدسی‌های نازک» (Thin Lenses) در هوا استفاده کرد که در آن $$n$$ ضریب شکست نور ورودی به لنز و $$R_{1}$$ شعاع انحنا است. $$R_{1}$$ در صورت محدب بودن سطح اول مثبت و در صورت مقعر بودن منفی در نظر گرفته می‌شود. در مورد $$R_{2}$$ یا سطح پشتی لنز موضوع عکس است. اگر سطح مقعر باشد $$R_{2}$$ مثبت و اگر محدب باشد $$R_{2}$$ منفی است.

$$\frac{1}{f}=(n-1)[\frac{1}{R_{1}}-\frac{1}{R_{2}}]$$

برای درک بهتر کمیت $$R_1$$ و $$R_2$$ شکل زیر را ببینید.

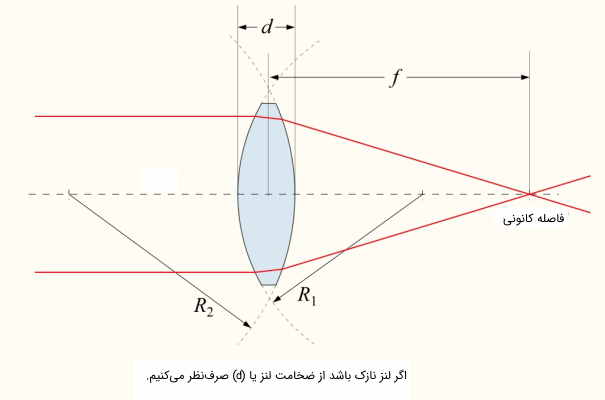
برای یک عدسی همگرا (محدب) فاصله کانونی همیشه مثبت است. همچنین در صورت مجازی بودن تصویر، علامت $$q$$ منفی است.

مثال

جسمی را در فاصله ۴ سانتی‌متری از یک عدسی همگرا دو کوژ (محدب) با فاصله کانونی ۸ سانتی‌متر قرار می‌دهیم. برای بدست آوردن موقعیت تصویر داریم:

$$\frac{1}{p}+\frac{1}{q}=\frac{1}{f} \rightarrow \frac{1}{4}+\frac{1}{q}=\frac{1}{8}\Rightarrow q=-8 cm$$

علامت منفی برای $$q$$ به منزله مجازی بودن آن است.

بزرگ‌نمایی عدسی

همانند آینه‌ها، نسبت طول تصویر به طول جسم را بزرگ‌نمایی تعریف می‌کنند.

$$m=\frac{h'}{h}$$

همچنین بزرگ‌نمایی یک عدسی را می‌توانیم نسبت اندازه $$q$$ به اندازه $$p$$ تعریف کنیم.

$$m=\frac{|q|}{p}$$

مثال (ذره‌بین)

دیدیم که هرگاه جسمی در فاصله کانونی یک عدسی محدب قرار گیرد (اولین شکل جدول)، در این صورت تصویری مجازی، مستقیم و بزرگ‌تر حاصل می‌شود. در این حالت این عدسی به عنوان ذره‌بین به کار می‌رود. حال فرض کنید که از جسمی به طول 0.5 سانتی‌متر توسط یک ذره‌بین می‌خواهیم تصویری به طول ۲ سانتی‌متر تهیه کنیم. اگر عدسی را در فاصله ۶ سانتی‌متری از جسم بگیریم، فاصله کانونی عدسی به کار رفته در آن چقدر است؟

$$m=\frac{h'}{h}=\frac{|q|}{p}\Rightarrow \frac{2}{0.5}=\frac{|q|}{6} \Rightarrow |q|=24cm$$

می‌دانیم که در این حالت تصویر مجازی است. پس علامت $$q$$ باید منفی باشد. حال از معادله اصلی عدسی داریم:

$$\frac{1}{p}+\frac{1}{q}=\frac{1}{f} \rightarrow \frac{1}{6}-\frac{1}{24}=\frac{1}{f} \Rightarrow f=8cm$$

توان عدسی

برای مقایسه عدسی بر اساس فاصله کانونی از واحدی به نام «دیوپتر» (Diopter) استفاده می‌کنند. عکس فاصله کانونی را توان عدسی می‌نامند که یکای آن عکس متر ($$\frac{1}{m}$$) است. در اپتیک $$\frac{1}{m}$$ را دیوپتر ($$D$$) می‌نامند. در واقع این پارامتر قدرت عدسی‌ها را در واگرایی یا همگرایی مشخص می‌کند. یک لنز همگرا با دیوپتر بالاتر، پرتوها را در فاصله کانونی کمتری همگرا می‌کند. در واقع عدسی همگرا (محدب) با فاصله کانونی کمتر توانایی بیشتری در همگرا کردن پرتوهای نوری دارد.

$$D=\frac{1}{f}$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های فیزیک
• آموزش جامع فیزیک دبیرستان
• مجموعه آموزش‌های ریاضیات
• ٰآموزش پایه ای عکاسی
• آینه مقعر در فیزیک — به زبان ساده
• آینه محدب (Convex Mirror) — به زبان ساده

^^