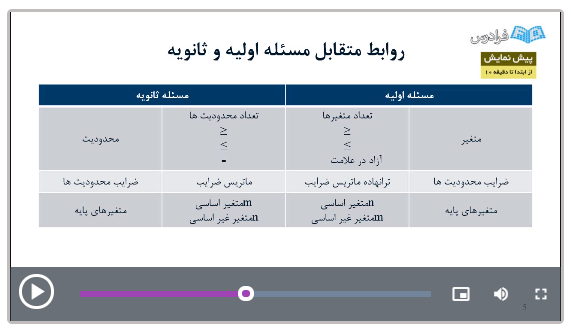
سیمپلکس دوگان — به زبان ساده

در آموزش‌های پیشین مجله فرادرس، با روش سیمپلکس اولیه آشنا شدیم که در آن، ستون سمت راست (RHS) همیشه نامنفی بود و به همین دلیل جواب اساسی یا پایه در هر تکرار شدنی بود. همچنین، وقتی برخی عناصر منفی بودند، دیدم که جواب پایه نشدنی است. با توجه به این نکته، ما همیشه با جواب‌های پایه شدنی سر و کار داشتیم. در الگوریتم سیمپلکس اولیه، برای پایان الگوریتم باید برخی عناصر در سطر $$0$$ منفی شوند تا شرایط بهینگی برقرار شود. در حالتی که همه عناصر این سطر نامنفی باشند، می‌گوییم پایه متناظر شدنیِ دوگان است. از طرف دیگر، اگر برخی عناصر سطر $$0$$ منفی باشند، یک پایه نشدنی دوگان داریم.همان‌طور که گفتیم، روش سیمپلکس اولیه با پایه‌های اولیه شدنی، اما دوگان نشدنی (غیربهینه) متناظر است. در جواب نهایی (بهینه)، پایه هم اولیه و هم دوگان، شدنی هستند. در این آموزش، یک رویکرد متفاوت، به نام روش «سیمپلکس دوگان» (Dual Simplex) یا سیمپلکس ثانویه بیان می‌کنیم که عکس روش اولیه کار می‌کند.

در روش سیمپلکس دوگان ، تا مرحله تکرار آخر، هر پایه آزمایش شده نشدنی اولیه (برخی عناصر سمت راست منفی) و شدنی دوگان (همه عناصر سطر $$0$$ نامنفی) است. در تکرار نهایی (بهینه)، هر دو جواب در اولیه و دوگان شدنی خواهد بود. در این فرایند، شدنی بودن دوگان را حفظ می‌کنیم و شدنی بودن اولیه را پیش می‌بریم. برای یک مسئله مشخص، هر دو الگوریتم سیمپلکس اولیه و ثانویه، علی‌رغم آنکه فرایند تکرار از مسیرهای متفاوتی انجام شده است، در جواب مشابهی خاتمه می‌یابند.

الگوریتم سیمپلکس دوگان اغلب برای مسائلی که در آن‌ها یک جواب شدنی دوگان به راحتی در دسترس است، مناسب خواهد بود. این روش، به ویژه برای بازبهینه‌سازی یک مسئله پس از افزودن یک قید یا تغییر پارامتری که منجر به نشدنی بودن جواب قبلی می‌شود، مناسب است. در ادامه، خواهیم دید که الگوریتم سیمپلکس دوگان بسیار شبیه الگوریتم سیمپلکس اولیه است.

الگوریتم سیمپلکس دوگان

با توجه به ماتریس یا جدول سیمپلکس، الگوریتم باید با یک جواب پایه یا اساسی شروع شود که شدنی دوگان است، بنابراین، همه عناصر سطر $$0$$ باید نامنفی باشند. الگوریتم سیمپلکس اولیه یک متغیر را برای وارد شدن به پایه انتخاب می‌کند و آنگاه متغیری را که باید خارج شود پیدا می‌کند، به گونه‌ای که شدنی بودن اولیه حفظ شود. روش سیمپلکس دوگان برخلاف این روش عمل می‌کند. در این روش، ابتدا یک متغیر برای خروج از پایه انتخاب می‌شود و آنگاه متغیری را پیدا می‌کند که باید وارد پایه شود تا شدنی بودن دوگان را حفظ کند. این موضوع، تفاوت اساسی بین این دو روش است. در الگوریتم زیر، فرض شده که یک جواب اساسی با یک جدول ارائه شده است.

فیلم آموزش الگوریتم سیمپلکس Simplex – به زبان ساده در فرادرس

کلیک کنید

گام اول (مقداردهی اولیه): با یک پایه شدنی دوگان شروع می‌کنیم و $$k = 1$$ را در نظر می‌گیریم. جدولی برای این پایه به فرم سیمپلکس تشکیل می‌دهیم. اگر درایه‌های ستون سمت راست همه نامنفی باشند، جواب شدنی اولیه خواهد بود، بنابراین، توقف می‌کنیم و به جواب بهینه می‌رسیم.

گام دوم (تکرار $$k$$): این گام شامل سه مرحله است.

الف) یک متغیر خارج شونده انتخاب کنید. یک سطر با یک ثابت سمت راست منفی پیدا کنید و آن را $$r$$ بنامید،؛ یعنی $$\bar {b} _ r < 0$$. اکنون $$r$$ را به عنوان سطر لولا و $$x _ {\text{B}(r)}$$ را به عنوان متغیر خارج شونده در نظر بگیرید. یک قانون متداول برای انتخاب $$r$$، انتخاب منفی‌ترین مقدار ستون سمت راست یا RHS است؛ یعنی:

$$\large \bar { b } _ { r } = \min \left \{ \bar { b } _ { i } : i = 1 , \ldots , m \right \}$$

ب) متغیر وارد شونده را تعیین کنید. برای هر ضریب منفی در سطر لولا، مقدار منفی نسبت بین هزینه کاهش یافته در سطر $$0$$ و ضریب ساختاری در سطر $$r$$ را محاسبه کنید.  اگر ضریب منفی، یعنی $$\bar{a} _ { rj} < 0$$ وجود نداشت، توقف کنید، زیرا جواب شدنی وجود ندارد.

فرض کنید ستونی که با حداقل نسبت و با شاخص $$s$$ مشخص شده، ستون لولا باشد. همچنین $$x _ S$$ متغیر ورودی است. ستون لولا با آزمون نسبت زیر تعیین می‌شود:

$$\large \frac { - \bar { c } _ { S } } { \bar { a } _ { r s } } = \min \left \{ \frac { - \bar { c } _ { j } } { \bar { a } _ { r j } } : \bar { a } _ { r j } < 0 , j = 1 , \ldots , n \right \}$$

ج) پایه را تغییر دهید. $$x _ { \text{B}(r)}$$ را با $$x _ S$$ جایگزین کنید. با انجام عملیات زیر یک جدول جدید ایجاد کنید (این موارد مشابه الگوریتم سیمپلکس ساده است).

$$\bar {\mathbf {a}} _ i$$ را به عنوان بردار $$i$$اُمین سطر جدول فعلی و $$\bar {\mathbf {a}} _ i ^{\mathrm {new}}$$ را به عنوان $$i$$اُمین سطر جدول جدید در نظر بگیرید. فرض کنید $$\bar {b} _ r$$ درایه سمت راست برای سطر $$i$$ در جدول فعلی و $$\bar { b } _ i ^ \text{new}$$ درایه سمت راست یا RHS برای جدول جدید باشد.

$$\bar {a} _ { iS}$$ را به عنوان عنصر $$i$$اُمین سطر ستون لولای $$s$$ در نظر بگیرید.

سطر لولا در جدول جدید به صورت زیر است:

$$\bar { \mathbf { a } } _ { r } ^ { \mathrm {new} } = \overline { \mathbf { a } } _ { r } / \bar { a } _ { r s } \text { , }\;\; \bar { b } _ { r } ^ { \text {new }} = \bar { b } _ { r } / \bar { a } _ { r s }$$

سطرهای دیگر در جدول جدید برای $$i=0,1, \ldots, m, i \neq r$$ به شکل زیر هستند:

$$\large \begin {array} { c } & - \mathbf { a } _ { i } ^ { \text {new}} = \left ( - \bar { a } _ { is} \times \overline{\mathbf{a}}_ { r } ^ { \text {new }}\right)+\overline{\mathbf{a}}_{i} \\ & \bar{b}_{i}^{\text {new}}=\left(-\bar{a}_{i s} \times \bar{b}_{r}^{\text {new}}\right)+\bar{b}_{i} \end{array}$$

این عملیات اثر قیمت‌گذاری ستون لولا را دارد. تعویض آن یک $$1$$ در سطر $$r$$ خواهد داشت و یک $$0$$ در سایر سطرهای دیگر مطابق فرم سیمپلکس.

گام سوم (آزمون امکان‌سنجی): اگر همه درایه‌های ستون سمت راست نامنفی باشند، جواب شدنی اولیه است، بنابراین، توقف کنید و جواب بهینه است. در غیر این صورت، $$k$$ را $$k + 1$$ قرار دهید و به گام دوم بازگردید.

مثال روش سیمپلکس دوگان

ساده‌ترین حالت زمانی رخ می‌دهد که یک پایه شدنی دوگان واضح وجود دارد و می‌توان از آن برای مقداردهی اولیه الگوریتم سیمپلکس دوگان استفاده کرد. مسئله زیر را در نظر بگیرید.

فیلم آموزش تحقیق در عملیات 1 – مرور و تست کنکور ارشد و دکتری در فرادرس

کلیک کنید

می‌خواهیم تابع هدف زیر را کمینه کنیم:

$$\large z=-5 x_{1}-35 x_{2}-20 x_{3}$$

با توجه به قیود زیر:

$$\large \begin {array} {ccc} x _ { 1 } & - x _ { 2 } & - x _ { 3 } & \leq - 2 \\ - x _ { 1 } & - 3 x _ { 2 } & & \leq - 3 \\ x _ { 1 } \geq 0 , & x _ { 2 } \geq 0 , & x _ { 3 } \geq 0 \end {array}$$

گام ۱: متغیرهای کمکی $$x _ 4$$ و $$x _ 5$$ را به دستگاه اضافه می‌کنیم که منجر به جدول نخست می‌شود که نشدنی اولیه است، اما شدنی دوگان است.

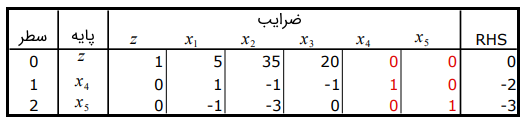
تکرار ۱: سطر ۲ به عنوان سطر لولا انتخاب می‌شود تا $$x _5$$ از پایه خارج شود. آزمون نسبت مشخص می‌کند که $$x _ 1$$ باید وارد پایه شود. شکل زیر جدول محاسبات نسبت را نشان می‌دهد.

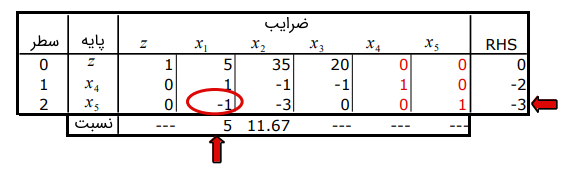
پس از عملیات ارزش‌گذاری برای به دست آوردن فرم سیمپلکس برای $$x _ 1$$، جدول زیر را خواهیم داشت. آزمون امکان‌سنجی در گام ۳ با شکست مواجه می‌شود، زیرا پایه هنوز شدنی اولیه نیست، بنابراین، به گام ۲ بازمی‌گردیم. گام‌های انتخاب سطر و ستون را برای تکرار بعدی نشان می‌دهیم.

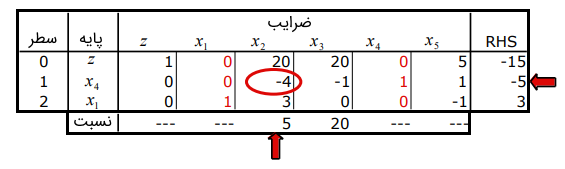
تکرار ۲: سطر ۱ به عنوان لولا انتخاب می‌شود، بنابراین، $$x _ 4$$ پایه را ترک می‌کند و $$x _ 2$$ به آن وارد می‌شود. این امر به جدول زیر می‌انجامد که هنوز دارای یک مقدار RHS منفی است، بنابراین، به گام ۲ بازمی‌گردیم.

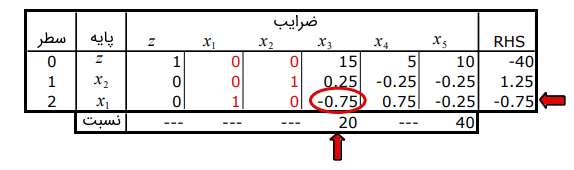
تکرار ۳: با انتخاب سطر ۲ به عنوان سطر لولا، $$x_ 1$$ از پایه خارج می‌شود و $$x _ 3$$ وارد می‌شود. جدول به‌روز شده در ادامه نشان داده شده است که هم شدنی اولیه است و هم دوگان و مشخص می‌کند که جواب بهینه به دست آمده است. الگوریتم به پایان رسیده‌ است.

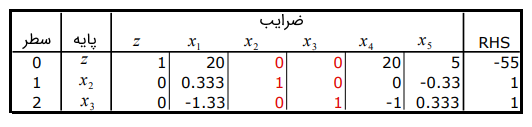
تغییر ثوابت سمت راست

اکنون می‌خواهیم ببینیم که پس از تغییر ثوابت سمت راست، باید چگونه عمل کنیم. یکی از کاربردهای الگوریتم سیمپلکس دوگان بازبهینه‌سازی یک مسئله حل شده پس از تغییر یک یا چند ثابت سمت راست آن است. این موضوع در مثال زیر توضیح داده شده است. جدول بهینه نیز با $$x _{s1}$$، $$x _ {s2}$$ و $$x _ { s 3 }$$ به عنوان متغیرهای کمکی نشان داده شده است.

مسئله زیر را در نظر بگیرید:

$$\large \begin {array} {lcc} \text { Maximize } z = & 2 x _ { 1 } & + 3 x _ { 2 } \\ \text { subject to } & - x _ { 1 } & + x _ { 2 } & \leq 5 \\ & x _ { 1 } & + 3 x _ { 2 } & \leq 3 5 \\ & x _ { 1 } & \leq 2 0 \\ & x _ { 1 } \geq 0 , x _ { 2 } \geq 0 \end {array}$$

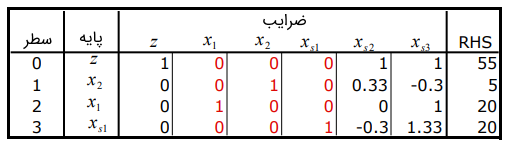
با تغییر ثوابت سمت راست، تنها درایه‌های ستون سمت راست جدول تغییر می‌کند. به ویژه، اگر $$b _ 2$$ را از $$35$$ به $$20$$ و $$b _ 3$$ را از $$20$$ به $$26$$ در مسئله اصلی تغییر دهیم، ستون RHS در جدول بالا برای پایه کنونی $$\mathbf {B}$$ به صورت زیر در خواهد آمد:

$$\large \mathbf { x } _ { \mathrm { B } } = \overline { \mathbf { b } } = \mathbf { B } ^ { - 1 } \mathbf { b } ^ { \mathrm {new} } = \left ( \begin {array} {rrr} - 1 & 1 & 1 \\ 1 & 3 & 0 \\ 1 & 0 & 0 \end {array} \right ) ^ { - 1 } \left ( \begin {array} { c } 5 \\ 2 0 \\ 2 6 \end {array} \right ) = \left ( \begin {array} { c } 2 6 \\ - 2 \\ 3 3 \end {array} \right ) \text {, }\;\;\; z = 4 6$$

در نتیجه، وقتی $$\mathbf { b } ^ { \mathrm {new} } = [5,20,26]^ T$$ با $$\mathbf { b } ^ { \mathrm {old} } = [5,35,20]^ T$$ جایگزین می‌شود، جدول زیر را خواهیم داشت که یک گزینه برای الگوریتم سیمپلکس دوگان است.

دقت کنید که $$\bar { b} _ 2$$ در سطر $$1$$ ظاهر می‌شود و $$\bar {b} _ 1$$ در سطر $$2$$ جدول است، زیرا سطر $$2$$ متناظر با $$x _ 1$$ و سطر $$1$$ متناظر با $$x_ 2$$ است.

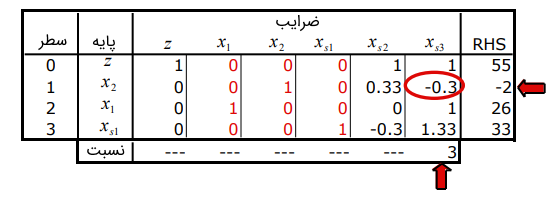
تغییر مقادیر RHS اثری بر هزینه‌های کاهش یافته ندارد، بنابراین، درایه‌های سطر $$0$$ نامنفی باقی می‌مانند؛ البته مقدار منفی $$\bar {b} _ 2$$ مشخص می‌کند که جواب پایه اکنون نشدنی است. از جدول واضح است که $$x _ 2$$ از پایه خارج شده و $$x _ { s 3 }$$ در تکرار بعد وارد می‌شود.

اضافه کردن قید

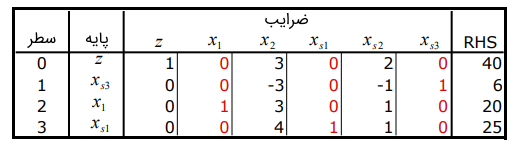
مسئله قبل را در نظر بگیرید. می‌خواهیم قید $$x _ 2 \ge 10$$ را به آن اضافه کنیم. جواب در جدول بهینه، یعنی $$x _ 1 = 20$$ و $$x _ 2 = 5$$، برای این قید برقرار نیست. بنابراین، باید آن را نیز به جدول وارد کنیم. ابتدا متغیر کمکی $$x _ { s 4 }$$ را از $$x _ 2$$ کم می‌کنیم تا تساوی زیر را به جای نامساوی داشته باشیم:

$$\large x _ 2 - x _ { s 4 } = 10$$

سپس آن را در $$-1$$ ضرب می‌کنیم تا به فرم صحیح برسیم. سطری که متناظر با این قید است و ستونی که متناظر با  متغیر کمکی است به جدول اضافه می‌کنیم و جدول زیر را خواهیم داشت.

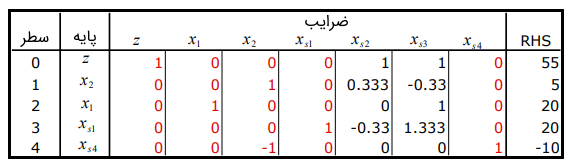
برای بازیابی فرم سیمپلکس برای ستون $$x _ 2$$، باید سطر $$1$$ را به سطر $$4$$ اضافه کنیم. اکنون جدول به فرم سیمپلکس است.

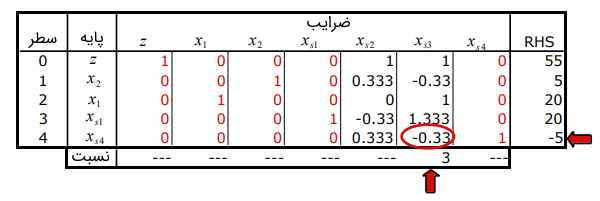
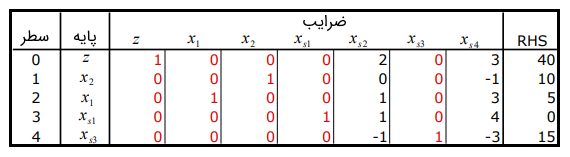
همان‌طور که انتظار می‌رود، جواب شدنی دوگان است، اما شدنی اولیه نیست. تنها مقدار RHS منفی در سطر $$4$$ ظاهر می‌شود، بنابراین، $$x _{ s4}$$ باید پایه را ترک کند. متغیر ورودی $$x_ {s3}$$ تنها گزینه با درایه منفی در سطر لولا است. جدول بهینه به شکل زیر است.

با استفاده از نرم‌افزار اکسل می‌توانید مسائل را به روش سیمپلکس به آسانی حل کنید. برای آشنایی با پیاده‌سازی روش سیمپلکس در اکسل، پیشنهاد می‌کنیم مطلب «سیمپلکس در اکسل — راهنمای کاربردی» را مطالعه کنید.

فیلم آموزش تحقیق در عملیات (برنامه ریزی خطی)

برای آشنایی بیشتر با روش سیمپلکس می‌توانید به دوره ویدیویی «آموزش تحقیق در عملیات (برنامه ریزی خطی)» مراجعه کنید. این آموزش ۲ ساعت و ۴۶ دقیقه‌ای، در ۵ درس ارائه شده است. در درس اول، مفاهیم برنامه‌ریزی خطی و مدل‌سازی شرح داده شده است. درس دوم به معرفی روش‌های حل مسائل برنامه‌ریزی خطی اختصاص یافته است. موضوع درس سوم، جبر ماتریسی و سیمپلکس اصلاح شده است. در درس چهارم، دوگان مسائل برنامه‌ریزی خطی به طور کامل توضیح داده شده است. در نهایت، تحلیل حساسیت و برنامه‌ریزی پارامتریک در درس پنجم معرفی شده است.

• برای دیدن فیلم آموزش تحقیق در عملیات (برنامه ریزی خطی) + اینجا کلیک کنید.