ذره بین چیست و چگونه کار می کند؟ – به زبان ساده
ذره بین همان طور که خواهیم گفت از عدسی بایکانوکس یا دو محدبی برای بزرگنمایی استفاده میکند. در این نوشتار در مورد ساختار ذره بین و ویژگیهای آن صحبت خواهیم کرد.


واژههای کلیدی در بررسی ذره بین
برای آشنایی با کار و ویژگیهای یک ذره بین لازم است که سه کلمه کلیدی که در ادامه از آنها زیاد استفاده میشود را معرفی کنیم.
- عدسی یا لنز: جسمی که معمولاً از شیشه ساخته شده و نوری که از آن عبور می کند را متمرکز یا پراکنده میکند.
- دیوپتر: واحد اندازه گیری قدرت لنز یا آینه و برابر با معکوس فاصله کانونی آن بر حسب متر است. نزدیک بینی بر حسب دیوپتر تشخیص و اندازه گیری میشود.
- عدسی محدب: مانند قسمت بیرونی کاسه یا کره یا دایرهای است که به سمت بیرون خم شده است.
همچنین قبل از شروع بحث در مورد ذره بینها و طرز کار آنها یادآوری سه نکته ضروری است:
- بزرگنمایی یک ذره بین بستگی به محل قرارگیری آن در بین چشم کاربر و شی مورد مشاهده و فاصله کلی بین چشم و جسم دارد.
- قدرت بزرگنمایی برابر با نسبت اندازه تصاویر است که روی شبکیه چشم کاربر با و بدون لنز تشکیل شده است.
- بالاترین قدرت بزرگنمایی با قرار دادن لنز بسیار نزدیک به چشم و تغییر فاصله چشم و لنز در کنار هم به دست میآید تا بهترین فوکوس حاصل شود.
ذره بین چیست؟
ذره بین یک لنز محدب است که به مشاهدهگر اجازه میدهد تصویر بزرگتری از جسم مورد مشاهده را با جزئیات بیشتری ببیند. همان طور که در تصویر زیر نشان داده شده است لنزها معمولاً در یک قاب با دسته بلند تهیه میشوند.

بزرگنمایی یک ذره بین بستگی به مکانی که عدسی بین چشم کاربر و شی مورد نظر قرار میگیرد و همچنین فاصله کلی بین چشم و جسم بستگی دارد. قدرت ذره بینی برابر با نسبت اندازه تصاویر ایجاد شده در شبکیه چشم کاربر با و بدون ذره بین است.
در صورت عدم استفاده از عدسی، کاربر معمولاً جسم را تا حد امکان بدون اینکه تار شود به چشم نزدیک میکند. این نقطه که به عنوان «نقطه نزدیک» (near point) شناخته میشود با توجه به سن فرد متفاوت است. در کودک خردسال این فاصله میتواند به اندازه پنج سانتی متر باشد، در حالی که در یک فرد بزرگسال این فاصله ممکن است به اندازه یک یا دو متر باشد. ذره بینها به طور معمول با استفاده از یک مقدار استاندارد 0٫25m یا ۲۵ سانتیمتری ساخته میشوند.
بالاترین قدرت بزرگنمایی با قرار دادن عدسی بسیار نزدیک به چشم و حرکت چشم و لنز در کنار هم تا رسیدن به بهترین فوکوس حاصل میشود. هنگامی که از این عدسی استفاده میشود، قدرت بزرگنمایی را میتوان با معادله زیر پیدا کرد:
که توان عدسی و برابر با معکوس فاصله کانونی است. وقتی ذره بین یا لنز محدب را نزدیک به جسم نگه داشته شود و چشم را حرکت دهیم بزرگنمایی ذره بین برابر است با:
ذره بینهای معمولی دارای فاصله کانونی ۲۵ سانتی متر هستند و توان اپتیکی آنها ۴ دیوپتر است. این نوع شیشهها تحت عنوان بزرگنمایی ۲ برابر و با علامت فروخته میشوند اما یک ناظر معمولی با استفاده از این ابزار میتواند بزرگنمایی یک تا دو برابر را داشته باشد که این موضوع بستگی به مکان عدسی دارد.
اولین شواهد در مورد دستگاه بزرگنمایی عدسی مربوط به ارسطوفان در سال 424 سال قبل از میلاد مسیح بوده است که در آن زمان از کرهای شیشهای پر از آب استفاده کردند. سنکا در این مورد نوشت که میتوان از این وسیله برای خواندن حروف هر چقدر کوچک یا کم نور باشد، استفاده کرد. «راجر بیکن» (Roger Bacon) خصوصیات ذره بین را در قرن سیزدهم توصیف کرد و همچنین عینکهای چشمی در قرن سیزدهم در ایتالیا تولید شدند.

ذره بین چگونه کار میکند؟
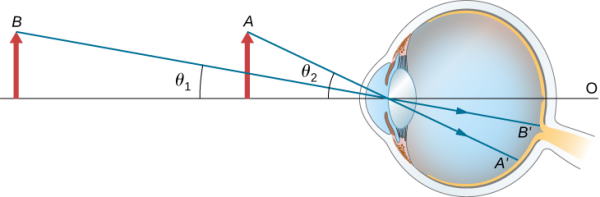
اندازه ظاهری جسمی که توسط چشم مشاهده میشود به زاویهای که جسم نسبت به چشم قرار گرفته بستگی دارد. همانطور که در شکل زیر نشان داده شده است، جسم در A در زاویه بزرگتری از چشم نسبت به موقعیت قرار گرفتن در نقطه B دارد. بنابراین جسم در نقطه A تصویر بزرگتری در شبکیه را () نسبت به زمانی که در B قرار گرفته است () را تشکیل میدهد. بنابراین اجسامی که پرتوهای نوری از آنها در زاویههای بزرگتری به چشم میرسند بزرگتر به نظر میرسند زیرا تصاویر بزرگتری را بر روی شبکیه تشکیل میدهند.
در مطلب عدسی چیست؟ نشان دادیم که وقتی جسمی در فاصله کانونی لنزهای محدب قرار میگیرد تصویر آن مجازی، قائم و بزرگتر از جسم است. بنابراین وقتی چنین تصویری که توسط یک عدسی محدب تولید میشود به عنوان جسم برای چشم عمل کند همان طور که در شکل زیر نشان داده شده است، تصویر بزرگتری در شبکیه ایجاد میشود زیرا تصویر تولید شده توسط لنز زاویه بزرگتری در چشم نسبت به شی را تولید میکند. در حقیقت عدسی محدبی که برای این منظور استفاده میشود شیشه ذره بین یا ذره بین ساده نامیده میشود.
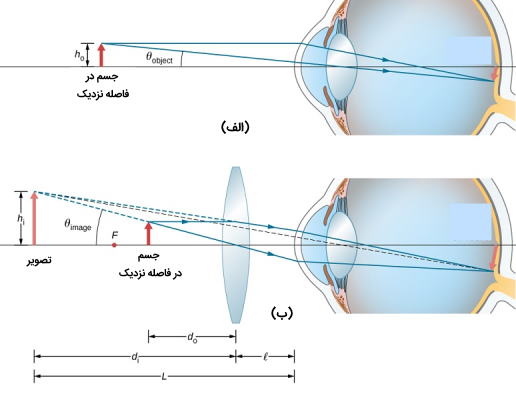
برای محاسبه بزرگنمایی یک ذره بین، زاویه تصویر را برای حالتی که از عدسی استفاده نکردهایم با حالتی که از عدسی استفاده کردهایم را با هم مقایسه میکنیم که این موضوع در شکل بالا نشان داده شده است.
در دو حالت فرض میکنیم جسم در نزدیکی چشم قرار گرفته است زیرا این حالتی است که چشم به صورت ساده میتواند بزرگترین تصویر را در شبکیه شکل دهد. با مقایسه اندازه تصویر در شبکیه برای حالتی که لنز در برابر چشم قرار گرفته است و حالتی که چیزی در برابر چشم قرار ندارد میتوان بزرگنمایی را محاسبه کرد.
بزرگنمایی یک تصویر که با چشم مشاهده میشود، بزرگنمایی زاویهای یعنی است که توسط نسبت بین زاویه تصویر نسبت به زاویه جسم بیان میشود و داریم:
حالتی که در تصویر بالا نشان داده شده است را در نظر بگیرید. در این حالت عدسی در فاصله از چشم قرار گرفته است و تصویری که با ذره بین تولید شده در فاصله از چشم قرار دارد. برای محاسبه بزرگنمایی زاویهای برای هر مقدار دلخواهی از و به صورت زیر عمل میکنیم.
با در نظر گرفتن تقریب زاویه کوچک که به معنی برابر بودن زاویه، سینوس و تانژانت زاویه مورد نظر است، داریم:
بنابراین اندازه زاویهای برای در نقطهای در نزدیکی آینه برابر با است. در نتیجه بزرگنمایی زاویهای برابر است با:
$$\large \underbrace{ M=\dfrac{θ_{image}}{θ_{object}}=\dfrac{h_i(25cm)}{Lh_o}}_{\text{angular magnification}} . \label{angular magnification}$$
با استفاده از رابطه بزرگنمایی خطی داریم:
از طرفی از تقریب لنز نازک میدانیم:
در نتیجه برای بزرگنمایی زاویهای یک ذره بین داریم:
$$\large \begin{align} M&= \left(−\dfrac{d_i}{d_o}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &=−d_i\left(\dfrac{1}{f}−\dfrac{1}{d_i}\right)\left(\dfrac{25\,cm}{L}\right) \\[4pt] &= \left(1−\dfrac{d_i}{f}\right)\left(\dfrac{25\,cm}{L}\right) \label{eq10} \end{align}$$
از تصویر در مییابیم که قدر مطلق فاصله تصویر تا لنز برابر با است. دقت کنید که است زیرا که تصویر موهومی و پشت عدسی تشکیل شده است، در نتیجه داریم:
با قرار دادن این مقدار به جای در معادله نهایی که به دست آوردیم، بزرگنمایی زاویهای برابر است با:
دقت کنید که در معادله بالا تمام کمیتها باید بر حسب سانتیمتر بیان شوند. برخی اوقات میخواهیم که تصویر در نزدیکترین فاصله باشد، برای این حالت یعنی باشد تا بیشترین بزرگنمایی را داشته باشیم و به این دلیل لنز را در کمترین فاصله از چشم یعنی قرار میدهیم. در این حالت معادله بزرگنمایی برابر است با:
که نشان میدهد بیشترین بزرگنمایی برای عدسیهایی با کوتاهترین فاصله کانونی رخ میدهد. به علاوه، وقتی تصویر در فاصله نزدیک است و عدسی نزدیک به چشم نگه داشته شده و است، و معادله بزرگنمایی به شکل زیر نیز نوشته میشود که به این معنی است که بزرگنمایی خطی و زاویهای در این حالت با هم برابر هستند و داریم:
که بزرگنمایی خطی است که برای عدسیها و آینهها نیز به دست میآید. حالت دیگری که شاید توضیح آن در این جا مفید باشد، زمانی است که تصویر در بی نهایت تشکیل شود و داشته باشیم . در این حالت معادله بزرگنمایی به شکل زیر در میآید:
همان طور که میبینید، در این حالت بزرگنمایی برابر با نسبت فاصله نزدیک و فاصله کانونی عدسی ذره بین است. در نتیجه عدسی با طول کانونی کوتاهتر، سبب بزرگنمایی بیشتری میشود. همچنین این بزرگنمایی یک واحد از بزرگنمایی تصویر در فاصله نزدیک کمتر است. این حالت بهترین و راحتترین حالت مشاهده برای چشم است، زیرا چشم وقتی به جسمی در دور نگاه میکند در آسودگی است.
با مقایسه روابطی که برای بزرگنمایی به دست آوردیم، میتوان دید که بزرگنمایی زاویهای عدسی در بازهای به صورت زیر تغییر میکند:
مثال: یک جواهرفروش میخواهد یک الماس با قطر 3 میلی متر را بررسی کند. الماس در نزدیکی چشم جواهر فروش (25 سانتی متر) نگه داشته شده و جواهرفروش عدسی بزرگنمایی را نزدیک چشم خود نگه میدارد.
- فاصله کانونی عدسی بزرگنمایی برای دیدن یک تصویر از الماس به قطر 15 میلی متر باید چه اندازه باشد؟
- فاصله کانونی لنز بزرگنمایی باید چه اندازه باشد تا بزرگنمایی 10 بدست آید؟
پاسخ: در ابتدا باید بزرگنمایی لازم ذره بین را تعیین کنیم. از آنجا که جواهرفروش عدسی بزرگنمایی را نزدیک چشم خود نگه میدارد، میتوانیم با استفاده از معادله مربوط به عدسی فاصله کانونی عدسی ذره بین را پیدا کنیم. برای حل قسمت اول این مثال باید در نظر بگیریم که بزرگنمایی خطی مورد نیاز، نسبت قطر تصویر مورد نظر به قطر واقعی الماس است. از آنجا که جواهرفروش عدسی بزرگنمایی را نزدیک چشم خود نگه میدارد و تصویر در نقطه نزدیک او تشکیل میشود، بزرگنمایی خطی همان بزرگنمایی زاویهای است و داریم:
فاصله کانونی را میتوان از رابطه بزرگنمایی به صورت زیر به دست آورد و داریم:
در نتیجه در این حالت فاصله کانونی برابر با ۶٫۳ سانتی متر است.
در قسمت دوم و برای به دست آوردن فاصله کانونی عدسی که بزرگنمایی به اندازه ۱۰ را بدهد، از رابطه بزرگنمایی داریم:
همان طور که مشخص است در این حالت فاصله کانونی ۲٫۸ سانتیمتر است.
حالتهای مختلف برای بزرگنمایی ذره بین
با توجه به توضیحات ارائه شده در بخش قبل برای بزرگنمایی ذره بین سه حالت را میتوان در نظر گرفت.
حالت اول
در شکل زیر و در حالت اول جسم به طور مستقیم توسط چشم در فاصله نزدیک مشاهده میشود. در این شکل N فاصله نزدیک برای چشم معمولی است و زاویه بین چشم و هر دو انتهای جسم و طول جسم است. در حالت دوم یک ذره بین قرار دادهایم و به جسم نگاه میکنیم. در این حالت فاصله بین جسم و عدسی، زاویه بین جسم و محور کانونی و ارتفاع جسم است. بدین ترتیب اگر تقریب زوایای کوچک را استفاده کنیم داریم:
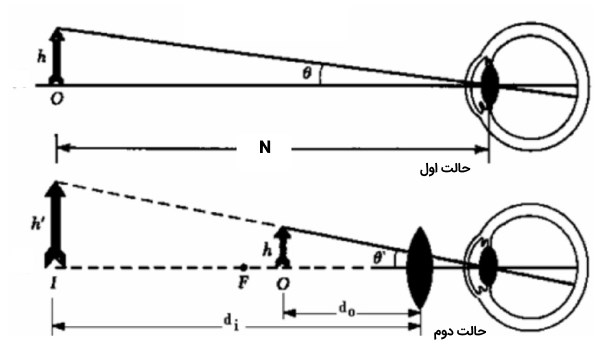
که M بزرگنمایی زاویهای است.
حالت دوم
در حالت دوم شرایطی را در نظر میگیریم که چشم در فاصله مینیمم از ذره بین قرار گرفته و تصویر در بی نهایت تشکیل میشود. در حقیقت به بیان دیگر باید گفت برای تشکیل تصویر در بی نهایت، فاصله بین جسم و ذره بین باید برابر فاصله کانونی ذره بین باشد. این دو حالت را در تصویر زیر نمایش داده ایم.
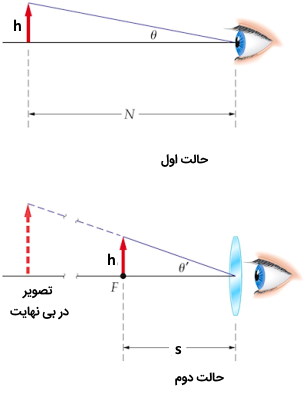
در این حالت برابر با فاصله کانونی عدسی است. در نتیجه نسبت به برابر است با:
که N فاصله نزدیک است و M بزرگنمایی زاویهای را میدهد.
حالت سوم
در حالت سوم شرایطی را در نظر میگیریم که تصویر در فاصله نزدیک تشکیل شود. در این حالت تصویر مجازی است. برای به دست آوردن فاصله جسم از معادله عدسیها داریم:
مجدداً با استفاده از تقریب زاویه کوچک مقدار تانژانت زاویه را با خود زاویه برابر در نظر میگیریم و داریم:
و بزرگنمایی زاویهای در این حالت برابر است با:
کاربردهای ذره بین چیست؟
ذره بین حدود سالهای 1250 در اروپا اختراع شد. امروزه بیش از 750 سال بعد از معرفی این اختراع به جامعه، ذره بینها در صدها سبک و اندازه وجود دارند که از این میان میتوان به مدلهای سبک اکریلیک برای استفاده در منزل تا لنزهای بزرگنمایی که در میکروسکوپهای پرقدرت برای تحقیقات علمی قرار گرفتهاند، نام برد. ذره بین به افراد دارای مشکلات بینایی و به متخصصانی مانند جواهرسازان و عکاسان در کار کمک میکند.

رفع مشکلات بینایی با ذره بین
از ذره بین اغلب برای کمک به افراد دارای مشکلات بینایی استفاده میشود. عینک نوعی ذره بین است که مشکلات مبینایی ختلفی از نزدیک بینی، دور بینی تا آستیگماتیسم را اصلاح میکند. افرادی که دچار دژنراسیون ماکولا یا مشکلات چشمی ناشی از گلوکوم یا دیابت هستند، اغلب از ذره بینهای دستی برای خواندن کتابها، روزنامهها و سایر اسناد چاپی استفاده میکنند. ذره بینهای نصب شده در دستگاههای خواندن که میتوانند اندازه مطالب چاپ شده را از سه برابر تا ده برابر اندازه طبیعی خود بزرگ کنند برای افرادی با بیماریهای مختلف چشمی بسیار مفید هستند.
ابزارهای علمی و پزشکی با ذره بین
میتوان ذره بینها را روی پایهها نصب کرد و میکروسکوپ تشکیل داد که دانشمندان مانند شیمی دانان و زیست شناسان از آنها برای انجام تحقیقات علمی استفاده میکنند. میکروسکوپ همچنین در تحقیقات پزشکی و در آزمایشگاههای پزشکی برای آزمایش خون و سایر مایعات بدن و بافتها استفاده میشود.
میکروسکوپها میتوانند اندازه اشیا را هزاران بار بزرگ کنند و دیدن ارگانها و عناصر انواع مختلف مواد را که با چشم غیر مسلح دیده نمیشوند ممکن میکند. برخی از میکروسکوپها مجهز به دوربینهایی هستند که این تصاویر بزرگنمایی شده را ضبط میکنند.
ابزار حرفهای با ذره بین
میکروسکوپ توسط متخصصانی مانند جواهرسازان و عکاسان در کارهای خود استفاده میشود. جواهرسازان سنگهای قیمتی را با دستگاههایی به نام «لوپس» (Loupes) ارزیابی میکنند که از سه عدسی بزرگنمایی مختلف سوار بر یک استوانه پلاستیکی تشکیل شده است. لوپس به جواهرفروشان اجازه میدهد تا نقصها و ناخالصیهایی را ببینند که میتواند بر ارزش الماس، زمرد و سایر سنگهای قیمتی تأثیر بگذارد. عکاسان همچنین برای ویرایش و ارزیابی عکسها از لوپس استفاده میکنند. با استفاده از یک لوپس، یک عکاس میتواند دانههای عکس را مشاهده کند که به او اجازه میدهد تا بداند که هنگام بزرگنمایی تا چه اندازه هر ناحیه تیز به نظر میرسد. لنزهای دوربین نیز اشکالی از ذره بین هستند که میتوانند اجسام دور را در عکس ها بزرگ کنند.
استفاده از ذره بین در خانه و برای سرگرمی
بسیاری از افراد برای سرگرمی، کاردستی و سایر کارهای روزمره در خانه از عینک ذره بینی استفاده میکنند. گردآورندگان سکه از ذره بین برای تشخیص سایش یک سکه استفاده میکنند که به تعیین ارزش آن کمک میکند.
گردآورندگان تمبر از ذره بین برای بررسی وضعیت و اصالت تمبرها استفاده میکنند. ذره بینهای بدون دسته که به پایه متصل هستند برای دوزندگی و کارهای خیاطی و بافندگی مفید هستند. ذره بین همچنین برای خواندن جزئیات روی نقشه و خواندن نوشتههای چاپی روی اسناد حقوقی مفید است.
چگونه میتوان ذره بین ساخت؟

در این قسمت به شما آموزش میدهیم که چگونه به راحتی و با کمترین امکانات یک ذره بین بسازید. ملزومات اولیه برای ساخت این ذره بین عبارتند از:
- یک بطری پلاستیکی تمیز
- ماژیک
- قیچی
- آب



بر روی بدنه بطری و روی قسمتی از بطری که انحنایی به سمت داخل دارد یک دایره رسم کنید. برای رسم این دایره بر روی بطری از یک جسم گرد استفاده کنید. دایره را ببرید و از بقیه بطری جدا کنید و بر روی دیسک دایرهای که ساختهاید کمی آب بریزید.
حالا دیسک را رو به روی صفحه یک کتاب عقب و جلو کنید تا کلمات را واضح و بزرگتر ببینید. وقتی این اتفاق افتاد و حروف را بزرگتر دیدید، باید به شما تبریک گفت چون شما یک ذره بین ساختهاید.
جایگزینهای ذره بین چه ابزاری هستند؟
ذره بینها معمولاً قدرت بزرگنمایی کمی بین تا دارند و انواع ذره بینها با قدرت بزرگنمایی کمتر در مصارف بسیار بیشتر دیده میشوند. در حقیقت در بزرگنماییهای بالاتر، کیفیت تصویر یک ذره بین ساده به دلیل انحرافات نوری و به ویژه انحرافات کروی، ضعیف میشود.
در صورت نیاز به بزرگنمایی بیشتر یا تصویر بهتر به طور معمول از انواع دیگر ذره بین دستی استفاده میشود. یک ذره بین «کدینگتون» (Coddington) بزرگنمایی بالاتری را با کیفیت تصویر بهبود یافته ارائه میدهد. تصاویر با کیفیت حتی بهتر را میتوان با قرار دادن یک ذره بین چند لنز مانند «سه قلوهای هاستینگز» (Hastings triplet) به دست آورد. ذره بینهای قدرت بالا گاهی اوقات در یک نگهدارنده استوانهای یا مخروطی بدون دسته نصب میشوند که به آنها لوپ میگویند.
بزرگنمایی در چنین ذره بینهایی میتواند به تا حدود 30 برابر برسد. در این مرتبه از بزرگنمایی، دیافراگم ذره بین بسیار کوچک میشود و باید خیلی نزدیک به جسم و چشم قرار گیرد. برای استفاده راحتتر یا بزرگنمایی بیشتر از حدود برابر باید از میکروسکوپ استفاده کرد.
انواع ذره بینها چه نام دارند؟
ذره بین را میتوان به سادگی و با استفاده از لنزهای شیشهای دوتایی محدب کروی ساخت. این ابزار برای یک میدان دید محدود میتواند یک راه حل راضی کننده باشد. از ابزارهای اپتیکی پلاستیکی (این مواد معمولاً از مواد آلی ساخته میشود و ترکیبات اصلی شیمیایی آن کربن، هیدروژن و اکسیژن است) اغلب به جای شیشه استفاده میشود و با این ابزار معمولاً ساختن لنزهای کروی مشکلی ندارد.
عینکهای آپلاناتیک، عینکهای متشکل از دو عدسی پلانوکانوکس هستند که در آنها سطح محدب در قسمت داخلی عدسی قرار دارد. این عینکها به عنوان عینکهای مطالعه معروف هستند زیرا انحراف تصویر کمی را به نمایش میگذارند.
عموماً ذره بینهای بزرگ معمولاً به صورت لنزهای فرنل ساخته شوند (یعنی ذره بینهایی با صفحات نازک) اما در این حالت کیفیت تصویر عموماً خیلی خوب نیست.
چه نوع لنزهایی در ذره بین استفاده می شود؟
وجه تمایز ذره بین ساختار آنها است. در حقیقت در یک ذره بین یک عدسی دو محدبی (عدسی که از هر دو طرف محدب است) در یک قاب قرار دارد و به یک دسته متصل است. در حقیقت اجزای اصلی ذره بین عدسی است و به همین دلیل گاهی به ذره بین عدسی نیز میگویند.
تفاوت ذره بین و میکروسکوپ چیست؟
تفاوت بین ذره بین و میکروسکوپ در بین تعداد عدسیهایی است که برای این دو ابزار به کار میرود. با یک ذره بین یا یک عدسی دستی، بزرگنمایی محدود به یک عدسی منفرد است. از آنجا که عدسی دارای یک فاصله کانونی است که از عدسی تا نقطه فوکوس عدسی تعریف میشود، بزرگنمایی عدسی ثابت است.
در سال 1673 «آنتونی ون لیوانهوک» (Antony van Leeuwenhoek) با استفاده از یک میکروسکوپ ساده یا لنز دستی با بزرگنمایی 300 برابر () اندازه واقعی، جهان را به یک موجود کوچک تشبیه کرد. اگرچه لیوانهوک از یک لنز دو مقعری استفاده کرده بود که وضوح تصویر (اعوجاج کمتری) بهتری ایجاد میکرد، اما در بیشتر ذره بینها از لنز محدب استفاده میشود.
یافتن بزرگنمایی در میکروسکوپهای مرکب مستلزم دانستن بزرگنمایی هر عدسی است که تصویر از آن عبور میکند و خوشبختانه بزرگنمایی هر لنز معمولاً روی آن مشخص است.
میکروسکوپهای معمولی کلاسهای درسی معمولاً دارای یک چشمی هستند که جسم را تا ۱۰ بار از اندازه واقعی جسم بزرگتر میکنند. معمولاً لنزهای هدف در میکروسکوپهای مرکب به یک دماغه چرخان متصل میشوند تا ناظر بتواند با چرخاندن دماغه مقدار بزرگنمایی و فوکوس را تغییر دهد.
برای یافتن بزرگنمایی کل یک دستگاه که از چندین لنز ساخته شده است، بایدبزرگنمایی لنزها را در هم ضرب کنید. اگر یک شی را از طریق یک عدسی هدف با کمترین توان مشاهده کنید، تصویر توسط عدسی هدف 4 برابر و توسط عدسی چشمی 10 برابر بزرگ میشود. بنابراین بزرگنمایی کل در این ابزار برابر با:
بنابراین تصویر 40 برابر () از اندازه واقعی بزرگتر است. برای آشنایی بیشتر با میکروسکوپ مطلب میکروسکوپ و انواع آن — به زبان ساده را مطالعه کنید.

مثالهای ذره بین
پرسش: اگر تصویر یک جسم زاویه ۳۰ درجه در شبکیه بسازد، در حالی که زاویه جسم در شبکیه ۵ درجه است. بزرگنمایی زاویهای این تصویر چه قدر است؟
پاسخ: با توجه به اینکه زاویه داده شده، بزگنمایی به راحتی برابر با نسبت بین زاویه تصویر و زاویه جسم است و برابر است با:
پرسش: بزرگنمایی زاویهای یک ذره بین با فاصله کانونی 14 سانتی متری اگر تصویری مجازی در فاصله نزدیک ایجاد کند چه قدر است (فرض کنید فاصله نزدیک ۲۵ سانتی متر است)؟
پاسخ: بزرگنمایی زاویهای در این حالت برابر است با:
با توجه به اینکه تصویر مجازی است پس خواهد بود. بنابراین فاصله جسم را با رابطه عدسی و به شکل زیر به دست میآوریم:
پرسش: یک برگه کاغذ را به دو قطعه که اندازه هر کدام یک میلی متر مربع است تقسیم کردهایم. این برگهها را در فاصله ۹ سانتی متری از یک ذره بین قرار میدهیم. طول کانونی عدسی به کار رفته در این ذره بین ۹ سانتی متر است و ذره بین نزدیک به چشم قرار گرفته است. الف) بزرگنمایی خطی که با لنز ایجاد میشود چه قدر است؟ مساحت جسم در تصویر مجازی چه قدر است؟ ب) بزرگنمایی زاویهای عدسی چه قدر است؟ ج) آیا بزرگنمایی قسمت (الف) و (ب) با هم برابر هستند؟
پاسخ: با توجه به رابطه حاکم بر عدسیها میتوانیم فاصله تصویر تا چشم را به دست آوریم.
بدین ترتیب بزرگنمایی عدسی برابر است با:
در نتیجه مساحت برگه کاغذ در تصویر مجازی تولید شده برابر با است و داریم:
ب) برای بزرگنمایی زاویهای با توجه به حالتهای گفته شده برای ذره بین، این شرایط از حالت اول پیروی میکند و داریم:
ج) همان طور که میبینید بزرگنمایی خطی و زاویهای یعنی قسمت الف و ب با یکدیگر برابر نیستند. این دو کمیت زمانی برابر هستند که تصویر در نزدیکی نقطه نزدیک شکل بگیرد.
پرسش: یک جسم با ارتفاع ۲ میلیمتر در فاصله ۱۰ سانتیمتری یک ذره بین قرار گرفته است. نقطه نزدیک برای این حالت ۲۵ سانتی متر است. طول تصویر و بزرگنمایی زاویهای را مشخص کنید.
پاسخ: مجدداً با مقایسه حالتهای گفته شده برای بزرگنمایی ذره بین و حالت گفته شده در مسئله بزرگنمایی زاویهای برابر است با:
و طول تصویر برابر با و برابر ۵ میلی متر میشود.
پرسش: یک لنز با فاصله کانونی ۲۵ سانتی متر به عنوان ذره بین به کار میرود. الف) بزرگنمایی زاویهای را در حالتی که تصویر در فاصله نزدیک تشکیل میشود، محاسبه کنید. ب) بزرگنمایی زاویهای را در حالتی که تصویر در بی نهایت تشکیل میشود، محاسبه کنید.
پاسخ: در حالتی که تصویر در فاصله نزدیک تشکیل میشود یعنی در مورد حالت سوم صحبت میکنیم. در این حالت بزرگنمایی زاویهای برابر است با:
ب) در حالتی که تصویر در بی نهایت تشکیل میشود با حالت دوم تشکیل تصویر در ذره بین رو به رو هستیم و بزرگنمایی زاویهای برابر است با:
جمع بندی
در این مطلب در مورد ذره بین و کاربردهای آن صحبت کردیم. برای شروع بحث ابتدا جند کلمه کلیدی و ویژگیهای مهم ذره بین را بیان کردیم. در ادامه در مورد ذره بین و فیزیک ذره بین توضیح دادیم و روند بزرگنمایی در ذره بین را بررسی کردیم. همچنین به معرفی کاربردهای ذره بین پرداختیم و در آخرین قسمت تفاوتهای بین ذره بین و میکروسکوپ را توضیح دادیم.













ممنونم عالی بود ابن مطلب✨️
سلام
من چندتا ذره بین با بزرگنمایی زیاد مثلاً 45 باز کردم دیدم دو عدسی داره که با فاصله تقریبا یک سانتیمتر از هم فیکس شدن ، محاسبات این مدل ذره بین رو میخوام تا یکی با قطر 10 برابر بسازم
خیلی به زبان ساده بود. بابا مغزم پوکید
چطور میشه ذره بین روی دو چشم قرار دهیم که بشه هر لحظه فاصله چه دور چه نزدیک تصویر واضحی نشان دهد؟
سلام و روز شما به خیر؛
این مورد هر روز در عینکها برای افرادی که دوربین یا نزدیک بین هستند رخ میدهد.
از اینکه با فرادرس همراه هستید خرسندیم.