دوقطبی الکتریکی (Electric Dipole) – به زبان ساده (+ دانلود فیلم آموزش رایگان)
در مقاله «محاسبه میدان الکتریکی -- به زبان ساده» با محاسبه میدان الکتریکی ساختارهای مختلف آشنا شدید. در راستای تکمیل مجموعه مقالات مجله فرادرس در خصوص فیزیک الکتریسیته و مغناطیس، در این مقاله در نظر داریم تا با زبانی ساده به دوقطبی الکتریکی (Electric Dipole) بپردازیم. با ما در ادامه این مقاله همراه باشید.
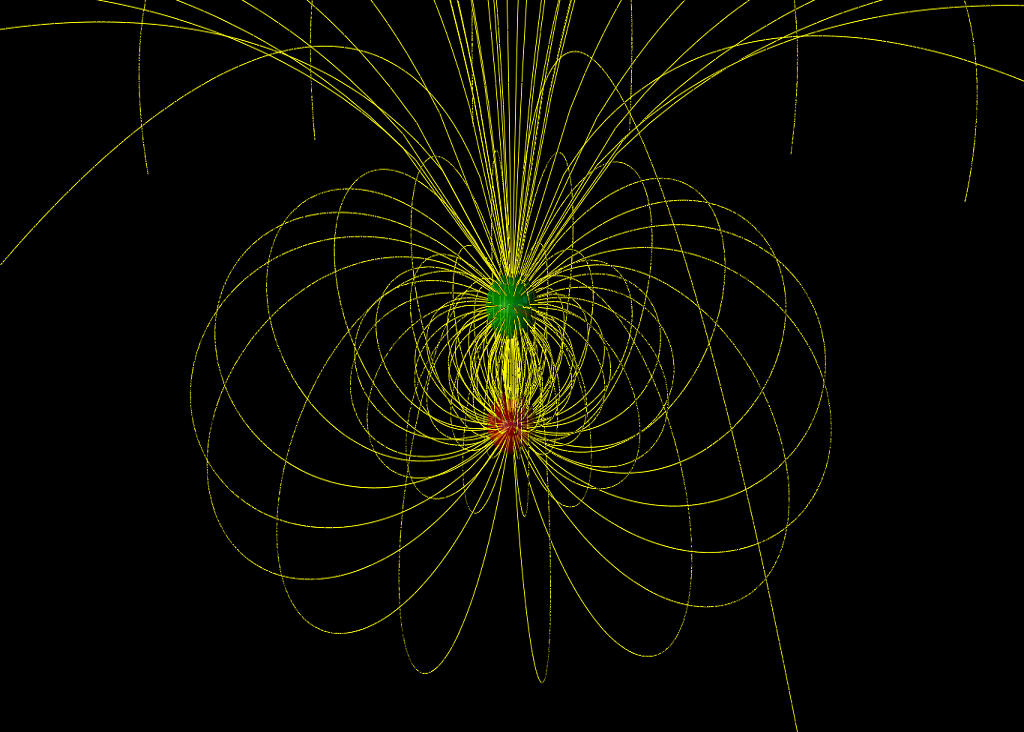
دوقطبی الکتریکی
به بیانی ساده، دو بار الکتریکی غیر همنام که در فاصله مشخصی از یکدیگر قرار گرفته باشند، تشکیل یک دوقطبی الکتریکی را میدهند.
همانطور که میدانید، شدت میدان الکتریکی را به طور کیفی با چگالی یا تراکم خطوط نشان میدهند. خطوط مذکور از بار الکتریکی مثبت خارج و به بار الکتریکی منفی وارد میشوند. شماتیک این خطوط به شکل زیر است:
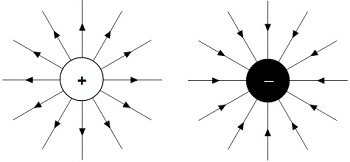
حال اگر دو بار الکتریکی غیر همنام (مثبت و منفی) در نزدیکی یکدیگر قرار گیرند، خطوط میدان الکتریکی به شکل زیر در میآید:
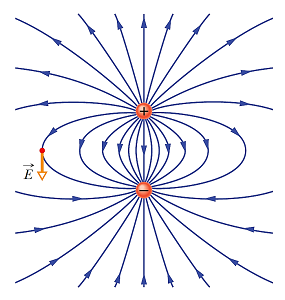
ساختار فوق، همان دوقطبی الکتریکی بوده که در ادامه قصد داریم میدان الکتریکی حاصل از آن را در نقطهای روی محور دوقطبی محاسبه کنیم.
میدان الکتریکی دوقطبی
فرض کنید که دو بار الکتریکی ناهمنام (مثبت و منفی) همانند شکل (3) در فاصله از یکدیگر قرار گرفته باشند.
همانطور که پیشتر اشاره کردیم، مجموعه مذکور تشکیل یک دوقطبی الکتریکی را میدهد که خطوط میدان از بار مثبت خارج و به بار منفی وارد میشود (شکل 2).
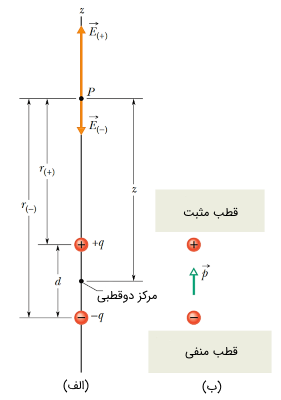
مطابق با شکل فوق، قصد محاسبه بردار میدان الکتریکی حاصل از این دوقطبی را در نقطه روی محور دوقطبی مذکور داریم. در اینجا فاصله نقطه تا مرکز دوقطبی () را با پارامتر نشان میدهیم. همچنین فاصله نقطه مذکور تا بار مثبت را با و تا بار منفی را با نشان میدهیم.
همانطور که میدانید، میدان الکتریکی حاصل از یک بار نقطهای در مکان به صورت زیر تعریف میشود.
(1)
(2)
(3)
از آنجایی که میدان الکتریکی از اصل برهمنهی پیروی میکند، میدان الکتریکی برآیند (کل) در یک نقطه، برابر با جمع میدان الکتریکی هر یک از بارها (در غیاب بارهای دیگر) در آن نقطه است. یعنی:
(4)
در اینجا تنها دو بار نقطهای مثبت و منفی داریم. در نتیجه:
(5)
بدیهی است که علامت منفی برای ، به دلیل این است که خطوط میدان بار منفی و مثبت در خلاف جهت یکدیگر هستند (بردارهای زرد رنگ در نقطه ). حال با توجه به رابطه (1 و ۵)، میدان الکتریکی دوقطبی در نقطه به صورت زیر نتیجه میشود:
(6)
طبق شکل (3)، دو فاصله و را میتوانیم به صورت زیر تعریف کنیم.
(7)
(8)
با جایگذاری پارامترهای فوق در معادله (6) و فاکتورگیری از عامل نتیجه میشود:
(9)
حال با استفاده از اتحاد ، میتوانیم قسمت پرانتزی رابطه فوق را به شکل زیر بنویسیم:
(10)
از آنجایی که معمولاً میدان الکتریکی در نقطهای دور از دوقطبی محاسبه میشود ()، حاصل عامل بسیار کوچکتر از یک شده و لذا میتوان از آن صرفنظر کرد. در نتیجه:
(11)
(12)
در رابطه فوق به عبارت ، تکانه یا ممان دوقطبی الکتریکی گفته شده که آن را با نمایش میدهند. طبق تعریف، واحد سنجش ، کولن متر است. جهت در یک دوقطبی همیشه از بار منفی به سمت بار مثبت است (شکل 3). لازم به ذکر است که برخی مراجع از بردار به عنوان گشتاور دوقطبی الکتریکی یاد میکنند و به ، گشتاور نیروی وارد بر دوقطبی میگویند. در ادامه مقاله با بردار آشنا خواهیم شد.
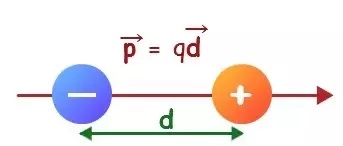
به طور کلی در فیزیک، تکانه یا ممان دو قطبی الکتریکی، مقیاسی جهت سنجش میزان جدایی بار الکتریکی مثبت و منفی در یک سیستم است. همچنین میزان پلاریزه (قطبی) شدن یک سیستم را بیان میکند. از آنجایی که را فاصله نقطه تا مرکز دوقطبی، یعنی در نظر گرفتیم، میتوان گفت که میدان الکتریکی دوقطبی تنها پارامتری از فاصله () بین دو بار مثبت و منفی است.
مثال: میدان الکتریکی دوقطبی روی خط عمود بر خط واصل
یک دوقطبی الکتریکی را مطابق با شکل زیر در نظر بگیرید. در اینجا قصد داریم تا میدان الکتریکی دوقطبی را در نقطه به دست آوریم.

با توجه به شکل فوق، فاصله هر کدام از بارهای مثبت و منفی تا نقطه از رابطه فیثاغورس در مثلثهای قائمالزاویهای که تشکیل میشود، به صورت زیر به دست میآید. در اینجا فاصله بار مثبت تا نقطه و فاصله بار منفی تا نقطه است.
(13)
(14)
در اینجا نیز به دلیل اینکه مقدار و فاصله تا نقطه برای هر دو قطب برابر است، میدان الکتریکی هر کدام از قطبها نیز در نقطه مذکور، با یکدیگر از لحاظ مقدار برابر هستند.
(15)
(16)
نکتهای که در اینجا باید به آن توجه کنید این است که سریعاً نمیتوان همانند رابطه (۶) دو مقدار فوق را با یکدیگر جمع کرد. چرا که دو بردار به دست آمده در یک راستا نبوده و قابل تجزیه به مولفههای و هستند. همانطور که در ابتدای مقاله بیان شد، خطوط میدان الکتریکی به بار منفی وارد و از بار مثبت خارج میشوند. در نتیجه با تجزیه بردار میدان الکتریکی در دو راستای و مطابق با شکل (6)، مولفههای راستای یکدیگر را خنثی کرده و تنها مولفههای راستای که در یک جهت هستند، با یکدیگر جمع میشوند.
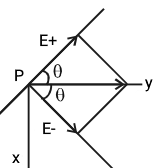
با توجه به شکل فوق، میدان الکتریکی هر یک از بارهای منفی و مثبت در راستای به صورت زیر در میآید. توجه داشته باشید که شکل (6) متناسب با محور مختصاتی شکل (5) بوده و جهت راحتی کار چرخانده شده است. به هرحال جهت به دست آوردن مولفه افقی یک بردار، باید آن را در کسینوس زاویه ضرب کرد که در این مسئله محور افقی، است. جهت آشنایی با بردارها به مقاله «بردار — به زبان ساده» مراجعه کنید.
(17)
(18)
در نتیجه میدان الکتریکی کل که در راستای محور است به صورت زیر نتیجه میشود.
(19)
دقت داشته باشید که دو مقدار و با یکدیگر برابر هستند. متناسب با شکل (۵ و ۶)، کسینوس زاویه () به صورت نتیجه میشود. در نتیجه:
(20)
در اینجا نیز همانطور که انتظار میرفت، نتیجهای همانند رابطه (۱۲) حاصل شد. در برخی از مثالهای دشوارتر که نقطه روی هیچکدام از محورهای و قرار ندارد (شکل 7)، محاسبات بسیار طولانی و پیچیده میشود. در این صورت پیشنهاد میشود که ابتدا پتانسیل الکتریکی کل را در نقطه مذکور به دست آورده و سپس با محاسبه گرادیان پتانسیل، میدان الکتریکی را به دست آوریم. همانطور که میدانید مولفه مکانی در رابطه پتانسیل، توان یک بوده که محاسبات را راحتتر میکند.
(21)
به طور مثال جهت یافتن میدان الکتریکی برآیند در نقطه در شکل زیر، ابتدا پتانسیل الکتریکی کل را محاسبه کرده و سپس از آن گرادیان میگیریم.
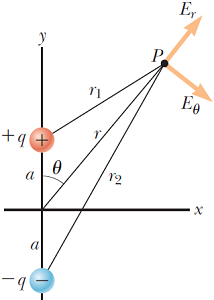
با توجه به شکل فوق داریم:
(22)
با فرض اینکه فاصله نقطه تا مرکز دوقطبی بسیار زیاد است ()، دو مقدار و را میتوانیم برابر با نظر بگیریم. همچنین با توجه به شکل داریم:
(23)
(24)
حال به راحتی با گرفتن گرادیان از عبارت فوق، میتوانیم میدان الکتریکی را محاسبه کنیم.
دوقطبی در میدان الکتریکی
در بخش قبل با تعریف ممان دوقطبی الکتریکی آشنا شدیم. همانطور که بیان کردیم، برداری است که از سمت بار منفی به سمت بار مثبت کشیده شده است. در این بخش قصد داریم تا یک دوقطبی الکتریکی را در میدان الکتریکی خارجی یکنواختی قرار داده و آن را بررسی کنیم. در اینجا خواهیم دید که بدون آنکه نیازی به دانستن جزئیات ساختار دوقطبی باشد، تنها با دو بردار و میتوانیم، رفتار دوقطبی را تحلیل کنیم.
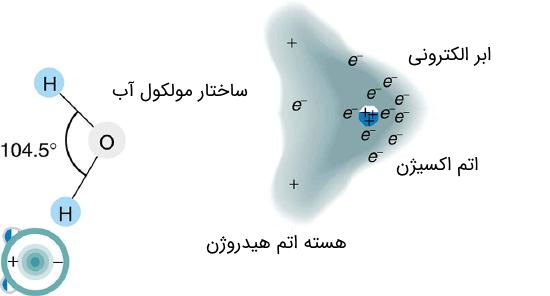
توجه داشته باشید که دوقطبی الکتریکی تنها محدود به تعریف ارائه شده در بخشهای قبلی نبوده و میتوان برای ساختارهای مولکولی نیز آن را تعمیم داد. به طور مثال آب، یک دوقطبی الکتریکی است. چرا که ساختار آن به صورتی است که بردار تکانه از چگالی بارهای منفی (الکترونها) در اتم اکسیژن به سمت چگالی بارهای مثبت (هسته) در دو اتم هیدروژن، رسم میشود. این امر در شکل (8) نشان داده شده است. جهت آشنایی با ساختار اتمها، به مقاله «اتم -- به زبان ساده» مراجعه فرمایید.
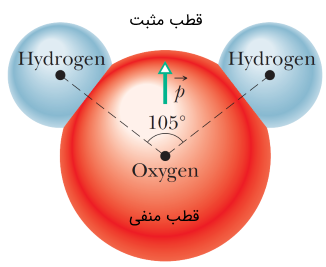
همانطور که در شکل فوق مشاهده میکنید، مولکول آب، مولکولی خطی نبوده و زاویه بین دو پیوند حدود 105 درجه است. مطابق با جدول تناوبی عناصر، اتم اکسیژن دارای ۸ پروتون و ۸ الکترون است. اتم هیدروژن نیز تنها دارای یک پروتون و یک الکترون است. به هنگام برقراری پیوند بین اتم اکسیژن با هر یک از اتمهای هیدروژن، تک الکترون اتم هیدروژن به سمت اتم اکسیژن آمده که در نتیجه چگالی بار منفی (مجموع الکترونها) در سمت اکسیژن زیاد میشود.
در این صورت اکسیژن قطب منفی مولکول شده و هستههای (پروتون) اتم هیدرژن، قطب مثبت مولکول را تشکیل میدهند. با این تفاسیر، مولکول آب یک دوقطبی الکتریکی را تشکیل میدهد که ممان دوقطبی الکتریکی از سمت اتم اکسیژن (قطب منفی) به سمت قطب مثبت کشیده میشود. لازم به ذکر است که به صورت خلاصه تنها عبارت مولکول قطبی برای این دست از مولکولها به کار میرود. جهت بررسی این مولکولها در میدان الکتریکی، به طور ساده ساختار را تنها شامل دو نقطه با بار مثبت و منفی در میگیریم.
در ادامه مطابق با شکل (10)، دوقطبی را در نظر بگیرید که مقدار بار دو قطب مثبت و منفی آن بوده و فاصله بین آن دو باشد. بردار ممان دوقطبی الکتریکی نیز با بردار میدان الکتریکی زاویه θ میسازد.
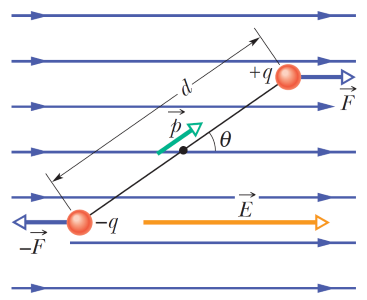
همانطور که میدانید، به بار الکتریکی که در میدان الکتریکی قرار داشته باشد، نیروی مطابق با رابطه وارد میشود. مطابق با شکل (10)، از آنجایی که بار هر دو قطب مثبت و منفی را فرض کردیم و میدان را نیز ثابت و یکنواخت در نظر گرفتیم، نیرو وارد شده به هر جز یکسان است (با علامت مخالف). در نتیجه نیروی کل وارد شده به سیستم صفر شده و مرکز جرم دوقطبی مذکور، حرکت نمیکند.
با اینکه مرکز جرم دوقطبی در میدان الکتریکی حرکت نمیکند، اما نیروهای وارد شده به انتهای دوقطبی باعث ایجاد گشتاور خالص در مرکز جرم دوقطبی میشوند. در اینجا مرکز جرم روی خط واصل دو قطب مثبت و منفی است. پیشتر بیان کردیم که فاصله بین دو قطب مثبت و منفی را در نظر میگیریم، در نتیجه نقطه مرکز جرم از یک سمت فاصله و از سمت دیگر دوقطبی فاصله را دارد. از مباحث فیزیک مکانیک به یاد دارید که گشتاور به صورت تعریف میشود. متناسب با فیزیک دوقطبی شکل (10) نتیجه میشود:
(25)
از رابطه فوق مشخص است که گشتاور وارد شده به سیستم دوقطبی به نقطه مرکز جرم وابسته نبوده و تنها به فاصله بین دو قطبی مثبت و منفی و نیرو ، بستگی دارد. نیروی نیز به صورت تعریف میشود. با توجه به تعریف ، رابطه (25) به صورت زیر نتیجه میشود:
(26)
(27)
سه بردار موجود در رابطه فوق، در شکل (11) نشان داده شدهاند. با توجه به رابطه فوق، گشتاور تمایل به کاهش زاویه θ و در نتیجه چرخش بردار به سمت بردار دارد. طبق شکل (10)، چرخش مذکور به طور ساعتگرد انجام میشود.
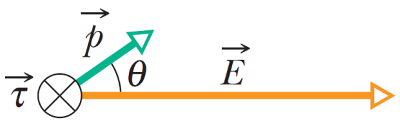
انرژی پتانسیل دوقطبی الکتریکی
در این بخش خواهیم دید که با انرژی پتانسیل، میتوانیم جهت یا سمتگیری دوقطبی الکتریکی را در میدان الکتریکی خارجی یکنواخت تعیین کنیم. انرژی پتانسیل دوقطبی الکتریکی به صورت زیر تعریف میشود:
(28)
(29)
با توجه به رابطه فوق، هنگامی که زاویه θ صفر درجه باشد، بردار ممان دوقطبی در جهت بردار خواهد بود که در این صورت انرژی پتانسیل حداقل مقدار خود یعنی را دارد. بدیهی است که در ، مطابق با رابطه (27)، گشتاور صفر میشود. همچنین در صورتی که باشد، بردارهای و در خلاف جهت یکدیگر خواهند بود. در حالت نیز گشتاور مقدار صفر را دارد (شکل 11). هنگامی که دوقطبی الکتریکی از زاویه به سمت زاویه سمتگیری یا تغییر جهت میدهد، کاری که میدان الکتریکی خارجی یکنواخت روی دوقطبی انجام میدهد، به صورت زیر قابل محاسبه است:
(30)
همچنین اگر تغییر سمتگیری مذکور توسط گشتاور نیرویی خارجی انجام شود، کاری که گشتاور نیروی خارجی روی دوقطبی الکتریکی انجام میدهد، منفی کاری است که میدان الکتریکی روی دوقطبی مذکور انجام میدهد ().
مثال
اگر هر مولکول آب () در حالت بخار دارای ممان دوقطبی الکتریکی باشد، فاصله مراکز بارهای مثبت و منفی در آن چقدر است؟
همانطور که میدانید مولکول آب (حالت خنثی) از یک اتم اکسیژن (۸ پروتون و ۸ الکترون) و دو اتم هیدروژن (مجموع ۲ پروتون و ۲ الکترون) تشکیل شده است. در نتیجه مقدار بار الکتریکی را میتوانیم مقدار در نظر بگیریم. با استفاده از رابطه ممان دوقطبی الکتریکی میتوانیم، مقدار را به صورت زیر محاسبه کنیم:
(31)
همانطور که مشاهده میکنید، مقدار به دست آمده حتی از شعاع اتم هیدروژن (شعاع بور) هم کمتر است. حال فرض کنید که مولکول آب مذکور را در میدان الکتریکی قرار میدهیم. در این حالت، مقدار ماکزیمم گشتاور نیرویی که به مولکول وارد میشود را میتوانیم به صورت زیر محاسبه کنیم:
(32)
حال میخواهیم مقدار کار عامل خارجی را در میدان مذکور، در حالتی که مولکول از حالت خطی به اندازه ۱۸۰ درجه بچرخد، محاسبه کنیم همانطور که بیان کردیم، کاری که عامل خارجی (از طریق گشتاور وارد بر مولکول) برابر با تغییر انرژی پتانسیل متناسب با تغییرات زاویه است. در نتیجه:
(33)
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مایکروویو (Microwave) یا ریز موج -- به زبان ساده
- امپدانس و محاسبه آن -- به زبان ساده
- خازن در جریان متناوب -- به زبان ساده
^^













سطوح هم پتانسیل دو قطبی چه شکلی دارند؟
درود وقت بخیر . ببخشید چرا به حاصل ضرب qd گشتاور دوقطبی الکتریکی میگیم و چرا حاصل ضرب qd برای ما مهم هستش که اون را در نتیجه با p نشون میدیم و این که جهت کمیت برداری گشتاور دوقطبی الکتریکی چرا از بار منفی به سمت بار مثبت هستش و چرا عکس اون نیستش ؟
با سلام،
دوقطبی الکتریکی کمیت بسیار مهمی در مطالعه میدان الکتریکی در محیط دیالکتریک است. از این کمیت، برای تحلیل امواج اپتیکی الکترومغناطیسی در موجبرها استفاده میشود. دقطبی الکتریکی برداری در راستای خط متصلکننده بارهای مثبت و منفی و جهت آن از بار منفی به بار مثبت است، زیرا دوقطبیها تمایل دارند در امتداد میدان الکتریکی محیط قرار بگیرند.
با تشکر از همراهی شما با مجله فرادرس
عالی
خییلی مفید بود دستتون درد نکنه