تبدیل خطی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در آموزش‌های قبلی مجله فرادرس درباره جبر خطی، با موضوعاتی مانند روش حذفی گاوس، استقلال خطی و عملیات سطری مقدماتی آشنا شدیم. در این آموزش، درباره نگاشت یا تبدیل خطی بحث خواهیم کرد.

تبدیل خطی

در این بخش، چند تعریف مربوط به تبدیل خطی را بیان می‌کنیم.

فیلم آموزش جبر خطی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

تعریف ۱

تابع $$T:\mathbb{R}^n \to \mathbb{R}^m$$ یک تبدیل خطی (Linear Transformation) نامیده می‌شود، اگر برای هر $$\mathbf{x}, \mathbf{y}\in \mathbb{R}^n$$ و $$c\in \mathbb{R}$$ در دو شرط خطی بودن زیر صدق کند:

1. $$T ( \mathbf { x } + \mathbf { y } ) = T ( \mathbf { x } ) + T ( \mathbf { y } )$$
2. $$T ( c \mathbf { x } ) = c T ( \mathbf { x } )$$

تعریف ۲

فضای پوچ (Nullspace) $$\mathcal{N}(T)$$ از تبدیل خطی $$T : \mathbb{R} ^ n \to \mathbb{R} ^ m$$ به صورت زیر است:

$$\large \mathcal{N} ( T ) = \{ \mathbf { x } \in \mathbb{R} ^ n \mid T ( \mathbf { x } ) = \mathbf { 0 } _ m \} .$$

تعریف ۳

پوچی (Nullity) تبدیل $$T$$، بُعد $$\mathcal{N}(T)$$ است.

تعریف ۴

برد $$\mathcal{R}(T)$$‌ مربوط به تبدیل خطی $$T:\mathbb{R}^n\to \mathbb{R}^m$$ برابر است با:

$$\large \mathcal{R} ( T ) = \{ \mathbf { y } \in \mathbb{R} ^ m \mid \mathbf { y } = T ( \mathbf { x } ) \text{ for some } \mathbf { x } \in \mathcal{R}^n\}.$$

تعریف ۵

رتبه $$T$$ برابر با بعد $$\mathcal{R}(T)$$ است.

تعریف ۶

نمایش ماتریسی تبدیل خطی $$T:\mathbb{R}^n \to \mathbb{R}^m$$، ماتریس $$A$$ با اندازه $$m \times n$$ است که برای همه $$\mathbf{x}\in \mathbb{R}^n$$ رابطه $$T(\mathbf{x})=A\mathbf{x}$$ برقرار است.

به طور خلاصه، فرض کنید $$T:\mathbb{R}^n \to \mathbb{R}^m$$‌ یک تبدیل خطی باشد. داریم:

1. رابطه $$T(\mathbf{0}_n)=\mathbf{0}_m$$ برقرار است، که در آن، $$\mathbf{0}_n$$ و $$\mathbf{0}_m$$، به ترتیب، بردارهای صفر در $$\mathbb{R} ^ n$$ و $$\mathbb{R}^m$$ هستند.
2. نمایش ماتریسی $$A$$‌ از تبدیل خطی $$T:\mathbb{R}^n \to \mathbb{R}^m$$ به صورت $$A=[T(\mathbf{e}_1), \dots, T(\mathbf{e}_n)]$$ داده می‌شود، که در آن، $$\mathbf{e}_1$$، $$\cdots$$ و $$\mathbf{e}_n$$ پایه‌های استاندارد برای $$\mathbb{R}^n$$ هستند.
3. اگر $$A$$ یک نمایش ماتریسی برای تبدیل خطی $$T$$ باشد، آنگاه:
   1. $$\mathcal{N}(T)=\mathcal{N}(A)$$ و $$\mathcal{R}(T)=\mathcal{R}(A)$$.
   2. پوچی $$A$$ برابر با پوچی $$T$$ است.
   3. رتبه $$T$$ برابر با رتبه $$A$$‌ است.

مثال‌ها

در این بخش، چند مثال را بررسی می‌کنیم.

فیلم آموزش جبر خطی – مرور و حل مساله در فرادرس

کلیک کنید

مثال ۱

دو تابع $$T:\mathbb{R}^{2}\to\mathbb{R}^{2}$$ و $$S:\mathbb{R}^{2}\to\mathbb{R}^{2}$$ به صورت زیر تعریف شده‌اند:

$$\large T \left( \begin {bmatrix} x \\ y \end {bmatrix} \right) = \begin {bmatrix} 2 x + y \\ 0 \end {bmatrix} , \; S \left( \begin {bmatrix} x \\ y \end {bmatrix} \right) = \begin {bmatrix} x + y \\ x y \end {bmatrix} .$$

خطی بودن تبدیل‌های $$T$$، $$S$$ و $$S\circ T$$ را بررسی کنید.

حل: برای بررسی اینکه $$T$$‌ یک تبدیل خطی است، ابتدا $$\mathbf{x},\mathbf{y}\in\mathbb{R}^{2}$$ را به صورت زیر می‌نویسیم:

$$\large \mathbf { x } = \begin {bmatrix} x _ { 1 } \\ x _ { 2 } \end {bmatrix} , \; \mathbf { y } = \begin {bmatrix} y _ { 1 } \\ y _ { 2 } \end {bmatrix} ,$$

در نتیجه، داریم:

$$\large \begin {align*} T \left( \mathbf { x } + \mathbf { y } \right) & = T \left( \begin {bmatrix} x _ { 1 } + y _ { 1 } \\ x _ { 2 } + y _ { 2 } \end {bmatrix} \right) = \begin {bmatrix} 2 ( x _ { 1 } + y _ { 1 } ) + ( x _ { 2 } + y _ { 2 } ) \\ 0 \end {bmatrix} \\ & = \begin{bmatrix} 2 x _ { 1 } + x _ { 2 } \\ 0 \end{bmatrix} + \begin {bmatrix} 2 y _ { 1 } + y _ { 2 } \\ 0 \end {bmatrix} = T ( \mathbf { x } ) + T ( \mathbf { y } ) . \end{align*}$$

برای هر عدد اسکالر $$r$$ نیز، داریم:

$$\large T ( r \mathbf { x } ) = T \left( r \begin {bmatrix} x _ { 1 } \\ x _ { 2 } \end {bmatrix} \right) = T \left( \begin {bmatrix} r x _ { 1 } \\ r x _ { 2 } \end{bmatrix} \right) = \begin {bmatrix} 2 r x _ { 1 } + r x _ { 2 } \\ 0 \end {bmatrix} = r \begin{bmatrix} 2 x _ { 1 } + x _ { 2 } \\ 0 \end{bmatrix} = r T ( \mathbf { x } ) .$$

در نتیجه، $$T$$ یک تبدیل خطی است.

اکنون $$S$$ را بررسی می‌کنیم. از آنجایی که ضرب متغیرها وجود دارد، این تبدیل خطی نیست. برای اثبات این گفته، تبدیل $$S$$ را با مقادیر عددی زیر در نظر بگیرید:

$$\large S \left ( \begin {bmatrix} 1 \\ 0 \end {bmatrix} \right ) = \begin {bmatrix} 1 \\ 0 \end {bmatrix} , \quad S \left ( \begin {bmatrix} 0 \\ 1 \end {bmatrix} \right ) = \begin {bmatrix} 1 \\ 0 \end {bmatrix} , \quad S \left ( \begin {bmatrix} 1 \\ 1 \end {bmatrix} \right ) = \begin {bmatrix} 2 \\ 1 \end {bmatrix} .$$

بنابراین، شرط $$S(\mathbf{x}+\mathbf{y})=S(\mathbf{x})+S(\mathbf{y})$$ برای همه $$\mathbf{x},\mathbf{y}\in\mathbb{R}^{2}$$ برقرار نیست. در نتیجه، $$S$$ یک تبدیل خطی نیست.

برای اثبات خطی بودن تبدیل $$S\circ T$$، عبارت آن را برای هر $$\mathbf{x}\in\mathbb{R}^{2}$$ به صورت زیر می‌نویسیم:

$$\large S \circ T ( \mathbf { x } ) = S \left ( T \left ( \begin {bmatrix} x \\ y \end {bmatrix} \right ) \right ) = S \left ( \begin {bmatrix} 2 x + y \\ 0 \end {bmatrix} \right ) = \begin {bmatrix} 2 x + y \\ 0 \end {bmatrix} = T ( \mathbf { x } ) .$$

همان‌طور که می‌بینیم، $$S\circ T=T$$ است. از آنجایی که $$T$$ یک تبدیل خطی است، نتیجه می‌گیریم $$S\circ T$$ نیز یک تبدیل خطی خواهد بود.

مثال 2

تابع $$T:\mathbb{R}^2 \to \mathbb{R}^3$$ به صورت زیر تعریف شده است:

$$\large T \left ( \, \begin {bmatrix} x \\ y \end {bmatrix} \, \right ) = \begin {bmatrix} x _ + y \\ x + 1 \\ 3 y \end {bmatrix}$$

بررسی کنید که آیا این تابع یک تبدیل خطی است یا خیر.

حل: همان‌طور که گفتیم، هر تبدیل خطی باید بردار صفر را به بردار صفر تبدیل کند. در صورتی که، داریم:

$$\large T \left ( \, \begin {bmatrix} 0 \\ 0 \end {bmatrix} \, \right ) = \begin {bmatrix} 0 + 0 \\ 0 + 1 \\ 3 \cdot 0 \end {bmatrix} = \begin {bmatrix} 0 \\ 1 \\ 0 \end {bmatrix} \neq \begin {bmatrix} 0 \\ 0 \\ 0 \end {bmatrix} .$$

بنابراین، تابع $$T$$ بردار صفر $$\begin {bmatrix} 0 \\ 0 \end {bmatrix}$$ را به بردار صفر $$\begin {bmatrix} 0 \\ 0 \\ 0 \end {bmatrix}$$ نمی‌نگارد.

یک راه‌حل دیگر این است که دو بردار زیر (یا هر دو بردار دیگری) را در نظر بگیریم:

$$\large \mathbf { u } = \begin {bmatrix} 1 \\ 0 \end {bmatrix} \text{, } \; \; \; \mathbf { v } = \begin {bmatrix} 0 \\ 1 \end {bmatrix} .$$

در نتیجه، خواهیم داشت:

$$\large T ( \mathbf { u } ) + T ( \mathbf { v } ) = T \left ( \, \begin {bmatrix} 1 \\ 0 \end {bmatrix} \, \right ) + T \left ( \, \begin {bmatrix} 0 \\ 1 \end {bmatrix} \, \right ) = \begin {bmatrix} 1 \\ 2 \\ 0 \end {bmatrix} + \begin {bmatrix} 1 \\ 1 \\ 3 \end {bmatrix} = \begin {bmatrix} 2 \\ 3 \\ 3 \end {bmatrix} .$$

از طرف دیگر، داریم:

$$\large T \left ( \, \mathbf { u } + \mathbf { v } \, \right ) = T \left ( \, \begin {bmatrix} 1 \\ 1 \end{bmatrix} \,\right) = \begin {bmatrix} 2 \\ 2 \\ 3 \end {bmatrix} .$$

بنابراین:

$$\large T ( \mathbf { u } ) + T ( \mathbf { v } ) \neq T \left ( \, \mathbf { u } + \mathbf { v } \, \right ) ,$$

و در نتیجه، $$T$$ یک تبدیل خطی نخواهد بود.

مثال 3

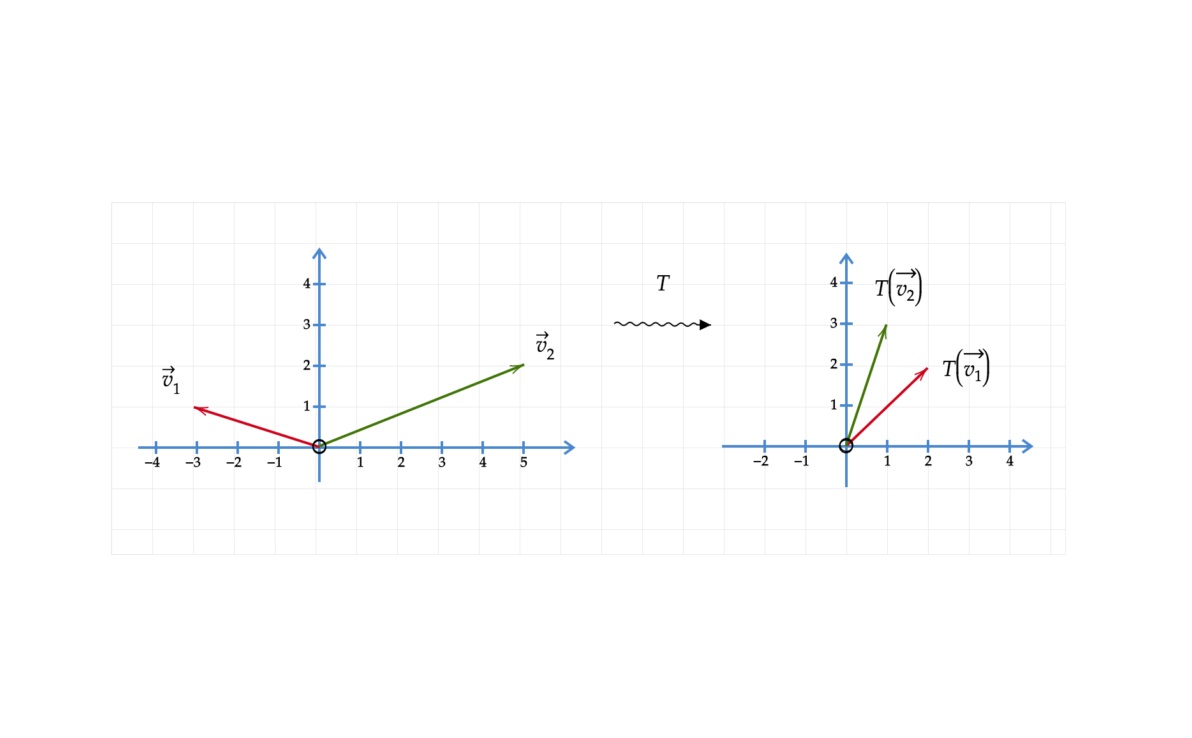
فرض کنید $$T: \mathbb{R}^2\to \mathbb{R}^2$$ یک تبدیل خطی است که بردارهای $$\mathbf{v}_1$$ و $$\mathbf{v}_2$$ را مطابق شکل زیر می‌نگارد.

نمایش ماتریسی $$A$$ را برای تبدیل $$T$$ به دست آورید.

حل: با توجه به شکل بالا، داریم:

$$\large \mathbf { v } _ 1 = \begin {bmatrix} - 3 \\ 1 \end {bmatrix} \text {, } \; \; \; \; \mathbf { v } _ 2 = \begin {bmatrix} 5 \\ 2 \end {bmatrix} ,$$

و

$$\large T ( \mathbf { v } _ 1 ) = \begin {bmatrix} 2 \\ 2 \end {bmatrix} \text {, } \; \; \; \; \; T ( \mathbf { v } _ 2 ) = \begin {bmatrix} 1 \\ 3 \end {bmatrix} .$$

ماتریس $$A$$ را به عنوان نمایش ماتریس تبدیل خطی $$T$$‌ در نظر می‌گیریم. طبق تعریف، برای هر $$\mathbf{x}\in \mathbb{R}^2$$ داریم: $$T(\mathbf{x})=A\mathbf{x}$$.

در ادامه، ماتریس $$A$$ را به دست می‌آوریم.

تساوی زیر را داریم:

$$\large \begin {align*} \begin {bmatrix} 2 & 1 \\ 2 & 3 \end {bmatrix} & = [ T ( \mathbf { v } _ 1 ) , T ( \mathbf { v } _ 2 ) ] \\ & = [ A \mathbf { v } _ 1 , A \mathbf { v } _ 2 ] \\ & = A [ \mathbf { v } _ 1 , \mathbf { v } _ 2 ] \\ & = A \begin {bmatrix} - 3 & 5 \\ 1 & 2 \end {bmatrix} . \end {align*}$$

دترمینان ماتریس آخر برابر با $$-11$$ بوده و در نتیجه، وارون‌پذیر است. وارون این ماتریس برابر است با:

$$\large \begin {bmatrix} - 3 & 5 \\ 1 & 2 \end {bmatrix} ^ { - 1 } = \frac { 1 } { 1 1 } \begin {bmatrix} - 2 & 5 \\ 1 & 3 \end {bmatrix}.$$

بنابراین، داریم:

$$\large \begin {align*} A & = \begin {bmatrix} 2 & 1 \\ 2 & 3 \end {bmatrix} \begin {bmatrix} - 3 & 5 \\ 1 & 2 \end {bmatrix} ^ { - 1 } \\[6pt] & = \frac { 1 } { 1 1 } \begin {bmatrix} 2 & 1 \\ 2 & 3 \end {bmatrix} \begin {bmatrix} - 2 & 5 \\ 1 & 3 \end {bmatrix} . \\[6pt] & = \frac { 1 } { 1 1 } \begin {bmatrix} - 3 & 1 3 \\ - 1 & 1 9 \end {bmatrix}. \end {align*}$$

در نتیجه، نمایش ماتریسی $$T$$ به صورت زیر خواهد بود:

$$\large A = \frac { 1 } { 1 1 } \begin {bmatrix} - 3 & 1 3 \\ - 1 & 1 9 \end {bmatrix} .$$

مثال 4

فرض کنید $$T$$ یک تبدیل خطی از فضای برداری سه‌بعدی $$\mathbb{R}^3$$ به $$\mathbb{R}^3$$ باشد که در روابط زیر صدق می‌کند:

$$\large \begin {align*} T \left ( \, \begin {bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} \, \right ) = \begin {bmatrix} 1 \\ 0 \\ 1 \end {bmatrix} , \qquad T \left ( \, \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} \, \right ) = \begin {bmatrix} 0 \\ 2 \\ - 1 \end{bmatrix}, \qquad T \left ( \, \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix} \, \right ) = \begin {bmatrix} 1 \\ 0 \\ 0 \end {bmatrix} . \end {align*}$$

برای هر بردار $$\mathbf { x } =\begin {bmatrix} x \\ y \\ z \end {bmatrix} \in \mathbb{R} ^ 3$$، فرمول $$T(\mathbf{x})$$ را به دست آورید.

حل: یک راه برای حل این مثال، استفاده از نمایش ماتریسی است. فرض کنید $$A$$ نمایش ماتریسی تبدیل خطی $$T$$ با توجه به پایه استاندارد از $$\mathbb{R}^3$$ باشد.

در نتیجه، طبق تعریف داریم: $$T(\mathbf{x})=A\mathbf{x}$$. ماتریس $$A$$ را به صورت زیر تعیین می‌کنیم:

$$\large \begin {align*} A \begin {bmatrix} 1 & 2 & 0 \\ 1 & 3 & 1 \\ 1 & 5 & 2 \end {bmatrix} & = \begin {bmatrix} A \begin {bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} , & A \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} , & A \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix} \\ \end {bmatrix} \\[6 pt] & = \begin {bmatrix} T \begin {bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} , & T \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} , & T \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix} \\ \end {bmatrix} = \begin {bmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & - 1 & 0 \end {bmatrix} . \end {align*}$$

در نتیجه، ماتریس $$A$$ برابر است با:

$$\large \begin {align*} A = \begin {bmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & - 1 & 0 \end {bmatrix} \begin {bmatrix} 1 & 2 & 0 \\ 1 & 3 & 1 \\ 1 & 5 & 2 \end {bmatrix} ^ { - 1 } . \end {align*}$$

ماتریس معکوس را با استفاده از ماتریس افزوده محاسبه می‌کنیم:

$$\large \begin {align*} \left[ \begin {array} {rrr|rrr} 1 & 2 & 0 & 1 &0 & 0 \\ 1 & 3 & 1 & 0 & 1 & 0 \\ 1 & 5 & 2 & 0 & 0 & 1 \\ \end {array} \right] \xrightarrow { \substack {R _ 2 - R _ 1 \\ R _ 3 - R _ 1 } } \left[\begin {array} {rrr|rrr} 1 & 2 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & - 1 & 1 & 0 \\ 0 & 3 & 2 & -1 & 0 & 1 \\ \end {array} \right] \\[6 pt] \xrightarrow { \substack { R _ 1 - 2 R _ 2 \\ R _ 3 - 3 R _ 2 } } \left[ \begin {array} {rrr|rrr} 1 & 0 & -2 & 3 &-2 & 0 \\ 0 & 1 & 1 & -1 & 1 & 0 \\ 0 & 0 & -1 & 2 & -3 & 1 \\ \end{array} \right] \xrightarrow { - R _ 3 } \left[ \begin {array} {rrr|rrr} 1 & 0 & - 2 & 3 &-2 & 0 \\ 0 & 1 & 1 & -1 & 1 & 0 \\ 0 & 0 & 1 & -2 & 3 & -1 \\ \end{array} \right] \\[6 pt] \xrightarrow { \substack { R _ 1 + 2R _ 3 \\ R _ 2 - R _ 3 } } \left[ \begin {array} {rrr|rrr} 1 & 0 & 0 & -1 &4 & - 2 \\ 0 & 1 & 0 & 1 & - 2 & 1 \\ 0 & 0 & 1 & - 2 & 3 & -1 \\ \end{array} \right]. \end{align*}$$

در نتیجه، ماتریس معکوس برابر است با:

$$\large \begin {bmatrix} 1 & 2 & 0 \\ 1 &3 &1 \\ 1 & 5 & 2 \end {bmatrix} ^ { - 1 } = \begin {bmatrix} - 1 & 4 & - 2 \\ 1 & - 2 & 1 \\ - 2 & 3 & - 1 \end {bmatrix}$$

و ماتریس $$A$$ به صورت زیر به دست می‌آید:

$$\large \begin {align*} A = \begin {bmatrix} 1 & 0 & 1 \\ 0 & 2 & 0 \\ 1 & - 1 & 0 \end {bmatrix} \begin {bmatrix} - 1 & 4 & - 2 \\ 1 & - 2 & 1 \\ - 2 & 3 & - 1 \end {bmatrix} = \begin {bmatrix} - 3 & 7 & - 3 \\ 2 & - 4 & 2 \\ - 2 & 6 & - 3 \end {bmatrix}. \end {align*}$$

با استفاده از رابطه $$T(\mathbf{x})=A\mathbf{x}$$، فرمول $$T(\mathbf{x})$$ به صورت زیر به دست می‌آید:

$$\large \begin {align*} T ( \mathbf { x } ) & = A \mathbf { x } \\ & = \begin {bmatrix} - 3 & 7 & - 3 \\ 2 & - 4 & 2 \\ - 2 & 6 & - 3 \end {bmatrix} \begin {bmatrix} x \\ y \\ z \end {bmatrix} \\[6 pt] & = \begin {bmatrix} - 3 x + 7 y - 3 z \\ 2 x - 4 y + 2 z \\ - 2 x + 6 y - 3 z \end {bmatrix} . \end {align*}$$

روش دوم حل این مثال، یافتن ترکیب خطی و استفاده از خاصیت خطی بودن تبدیل خطی است:

$$\large \mathbf{x}=c_1\begin{bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} + c _ 2 \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} + c _ 3 \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix}$$

برای به دست آوردن ضرایب $$c _ 1$$، $$c _ 2$$ و $$c _ 3$$، ماتریس افزوده زیر را می‌نویسیم:

$$\large \left[ \begin {array} {rrr|r} 1 & 2 & 0 & x \\ 1 &3 & 1 & y \\ 1 & 5 & 2 & z \end {array} \right]$$

عملیات کاهش دقیقاً مشابه راه‌حل اول هستند و داریم:

$$\large \begin {align*} c _ 1 & = - x + 4 y- 2 z \\ c _ 2 & = x - 2 y + z \\ c _ 3 & = - 2 x + 3 y - z . \end {align*}$$

بنابراین، با استفاده از خاصیت خطی بودن $$T$$، خواهیم داشت:

$$\large \begin {align*} T ( \mathbf { x } ) & = T \left ( \, c _ 1 \begin {bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} + c _ 2 \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} + c _ 3 \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix} \, \right ) \\[6 pt] & = c _ 1 T \left ( \, \begin {bmatrix} 1 \\ 1 \\ 1 \end {bmatrix} \, \right ) + c _ 2 T \left ( \, \begin {bmatrix} 2 \\ 3 \\ 5 \end {bmatrix} \, \right ) + c _ 3 T \left ( \, \begin {bmatrix} 0 \\ 1 \\ 2 \end {bmatrix} \, \right ) \\[6 pt] & = ( - x + 4 y - 2 z ) \begin {bmatrix} 1 \\ 0 \\ 1 \end {bmatrix} + ( x - 2 y + z ) \begin {bmatrix} 0 \\ 2 \\ - 1 \end {bmatrix} + ( - 2 x + 3y - z ) \begin {bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\\[6 pt] &=\begin{bmatrix} -3x+7y-3z \\ 2x-4y+2z \\ -2x+6y-3z \end{bmatrix}. \end{align*}$$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• آموزش جبر خطی با متلب
• تجزیه مقادیر منفرد (SVD) — به زبان ساده
• همنهشتی مثلث ها در هندسه — به زبان ساده
• تقلب نامه (Cheat Sheet) جبر خطی برای یادگیری ماشین — راهنمای سریع و کامل

^^