واریانس و اندازههای پراکندگی – به زبان ساده
در این مطلب از مجله فرادرس در مورد واریانش و اندازههای پراکندگی به زبان ساده صحبت میکنیم. شاخصهای آمار توصیفی، مانند شاخصهای تمرکز و یا اندازههای پراکندگی به منظور شناخت جامعه آماری به کار میروند. ولی استفاده از هر یک به تنهایی ممکن است نتیجه مناسبی نداشته باشد. توجه همزمان به معیارهای تمرکز و پراکندگی کمک میکند که بهتر جامعه آماری شناخته شده و رفتار آن قابل مقایسه و تحلیل باشد.
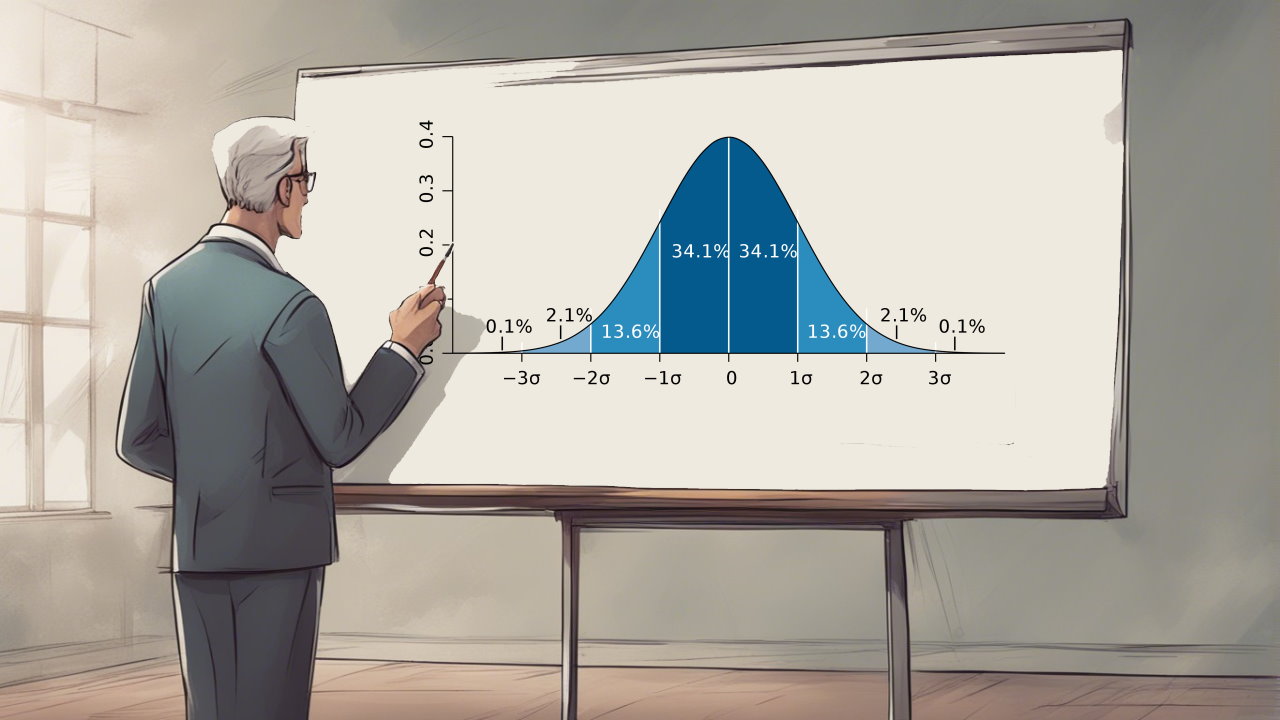
معیارهای تمرکز، نشان میدهند که دادهها، حول چه مقداری متمرکز هستند ولی بررسی نقطه تمرکز به تنهایی ممکن است محقق را به گمراهی بکشد.
مثال
فرض کنید نمرات دانشجویان دو مدرس در تدریس آمار طبق جدول زیر ثبت شده باشد.
| مدرس | دانشجو۱ | دانشجو۲ | دانشجو۳ | دانشجو۴ | دانشجو۵ | دانشجو۶ | دانشجو۷ | دانشجو۸ | میانگین |
| مدرس الف | 15 | 18 | 12 | 13 | 17 | 14 | 16 | 15 | 15 |
| مدرس ب | 10 | 18 | 20 | 10 | 20 | 20 | 12 | 10 | 15 |
اگر برای ارزیابی دو مدرس از شاخص میانگین استفاده شود، به نظر میرسد که هر دو دارای یک امتیاز باشند. در حالیکه دیده میشود در کلاس «مدرس الف» نمرات از یکدستی بیشتری برخوردار هستند و باوجود معدل ۱۵ در کلاس «مدرس ب»، نمرات پراکندگی بیشتری دارند که ممکن است نشان از عدم نظم در تدریس درس آمار داشته باشد.
برای اینکه بتوان قضاوت بهتری برای ارزیابی این مدرسها داشت، بهتر است علاوه بر شاخص میانگین از معیارهای دیگری مانند اندازه پراکندگی استفاده شود. در ادامه به معرفی چند اندازه پراکندگی میپردازیم که از شهرت بیشتری برخوردارند.
دامنه تغییرات
یکی از روشهای اندازهگیری پراکندگی بین دادهها، محاسبه «دامنه تغییرات» (Range) است. این شاخص، حداکثر میزان پراکندگی را نشان میدهد و برای محاسبه آن کافی است که تفاوت بین بزرگترین و کوچکترین مقدار را بدست آورد. اگر دامنه تغییرات را با R نشان دهیم، فرمول محاسباتی آن برای دادههای a1,a2,a3,a4,a5 به صورت زیر است:
$$R= \mbox{Max}(a_1,a_2,a_3,a_4,a_5)-\mbox{Min}(a_1,a_2,a_3,a_4,a_5)$$
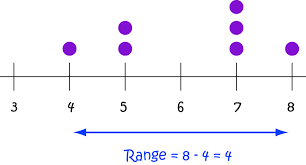
بنابراین طبق دادههای جدول مربوط به نمرات دانشجویان که در بالا ذکر شد، میزان پراکندگی نمرات برای «مدرس الف» برابر با 6=12-18 نمره است در حالیکه برای «مدرس ب» 10=10-20 خواهد بود. مشخص است که میزان پراکندگی برای «مدرس ب» بیشتر است که نشان دهنده عدم توازن در تدریس او محسوب میشود.
مزایا و معایب
- مزایا
- سادگی در محاسبه دامنه تغییرات
- نمایش حداکثر میزان پراکندگی
- معایب
- عدم محاسبه پراکندگی حول یک مرکز
- تاثیر پذیری زیاد از مقادیر خیلی بزرگ و یا خیلی کوچک
هر چند سادگی محاسبات برای این شاخص از ویژگیهای مهم آن است. ولی متاسفانه فقط بر اساس دو مقدار محاسبه میشود و بقیه مقدارها در تعیین این معیار نقشی ندارند.
دامنه میان چارکی
برای آنکه بتوان مشکل تاثیر پذیری دامنه تغییرات از مقدارهای بزرگ و کوچک را از بین برد، میتوان فاصله بین بزرگترین و کوچکترین مقدار را براساس چارکها محاسبه کرد. به این ترتیب برای دادههایی که دارای مقدارهای دور افتاده هستند، فاصله بین چارک اول و سوم، میتواند برآورد بهتری برای محاسبه حداکثر پراکندگی دادهها بدست دهد. به این شاخص «دامنه میان چارکی» (InterQuartile Range - IQR) میگویند. شکل محاسباتی دامنه میان چارکی به صورت زیر است:
که در آن Q1 چارک اول و Q3 چارک سوم است. برای مثال مربوط به دادههای نمرات دانشجویان، برای «مدرس الف» مقدار IQR =3 و برای «مدرس ب» مقدار IQR = 10 خواهد بود که باز هم نشاندهنده عدم یکدستی نمرات برای «مدرس ب» است. به منظور آشنایی بیشتر با شیوه محاسبه چارکها میتوانید مطلب صدک ها – مفاهیم ریاضی به زبان ساده را مطالعه کنید.

مزایا و معایب
- مزایا
- عدم تاثیر پذیری زیاد از مقادیر خیلی بزرگ و یا خیلی کوچک (حذف اثرات نقاط دور افتاده)
- سادگی در محاسبه (براساس مقدار چارک اول و سوم)
- معایب
- عدم محاسبه پراکندگی حول یک مرکز
- مقدارهای به جز چارک اول و سوم در محاسبه آن نقشی ندارند.
متوسط قدر مطلق انحرافات
معمولاً در صحبتهای روزمره، زمانی که از فاصله یا پراکندگی صحبت میشود، میگویم این دو شهر نسبت به هم دور هستند یا روستاهای این استان نسبت به مرکز شهرستان فاصله زیادی دارند. همانطور که دیده میشود پراکندگی یا فاصله را نسبت به یک نقطه در نظر میگیریم.
دامنه تغییرات و دامنه میان چارکی، معیارهای مناسبی برای اندازهگیری پراکندگی نیستند زیرا پراکندگی را نسبت به نقطهای خاص در نظر نمیگیرند. برای رفع این مشکل بهتر است نقطهای از دادهها را به عنوان مرکز در نظر گرفت و فاصله بقیه دادهها را نسبت به آن سنجید.
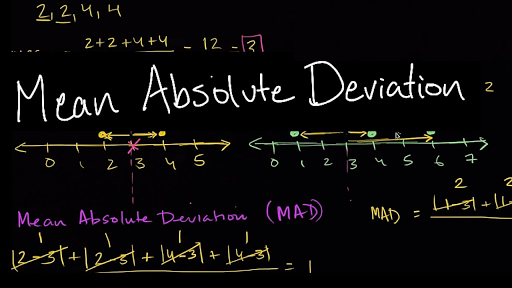
در محاسبه اندازه متوسط قدر مطلق انحرافات، اگر نقطه مرکزی، میانگین در نظر گرفته شود به آن «متوسط قدر مطلق انحرافات از میانگین» (Mean Deviation - MD) گفته میشود. البته ممکن است آن را با «قدر مطلق فاصله» (Absolute Difference from Mean - A.D) نیز نشان داد. برای محاسبه این شاخص کافی است میانگین دادهها محاسبه شده و قدر مطلق فاصله آنها نسبت به میانگشان ثبت شود، سپس میانگین این فاصلهها حساب شود.
از آنجایی که میانگین، نقطهای است که میانگین فاصله دادهها نسبت به آن صفر است، برای محاسبه MD از قدر مطلق فاصلهها استفاده میشود تا فقط مقدار فاصله، بدون در نظر گرفتن جهت آن، به کار رود. پس میتوان فرمول محاسباتی زیر را برای MD یا A.D نوشت:
نکته: اگر به جای میانگین از میانه به عنوان نقطه مرکزی استفاده شود به آن «متوسط قدر مطلق انحرافات از میانه» (Median Absolute Difference- MAD) میگویند. با توجه به تعریف میانه، مشخص میشود که مجموع فاصلههای به ازای قرار دادن میانه به جای a کمترین مقدار خود را خواهد داشت. فرمول محاسباتی برای MAD به صورت زیر است:
براساس مثال نمرات دانشجویان میزان پراکندگی براساس میزان MD برای کلاس «مدرس الف» برابر با 1.5 و برای «مدرس ب» 4.5 خواهد بود. همچنین میزان پراکندگی بر منبای MAD نیز برای «مدرس الف» و برای «مدرس ب» با مقدار MD آنها برابر است (میانه و میانگین نمرات هر دو مدرس با هم برابر هستند).
مزایا و معایب
- مزایا
- استفاده از یک نقطه مرکزی برای سنجش انحرافات
- نقش همه مقدارها در محاسبه پراکندگی
- معایب
- تاثیرپذیری از مقدارهای خیلی بزرگ و یا خیلی کوچک
- وابستگی به واحد اندازهگیری دادهها
- پیچیدگی در استفاده از روشهای ریاضی
نکته: اگر مقیاس اندازهگیری دادهها تغییر کند، یعنی همه مقدارها در عدد ثابت نامنفی ضرب یا تقسیم شوند، مقدار دامنه تغییرات، دامنه میان چارکی و MD یا MAD نیز در آن مقدار ضرب یا تقسیم خواهند شد ولی با اضافه یا کم شدن مقدار ثابت به دادهها، تغییری در این اندازههای پراکندگی بوجود نمیآید.
واریانس
از آنجایی که کارهای محاسباتی نظیر انتگرال و مشتق برای تابع قدر مطلق با مشکلاتی همراه است، برای نامنفی کردن فاصلهها نسبت به میانگین، میتوان از مربع آنها استفاده کرد. به این صورتِ محاسبه میزان پراکندگی، «واریانس» (Variance) میگویند. اگر میانگین جامعه آماری را با نشان دهیم، شکل محاسباتی برای واریانس که با نماد Var یا مشخص میشود، به صورت زیر است.
نکته: با توجه به تعریف میانگین و مشتقگیری میتوان نشان داد که مجموع فاصلههای به ازای قرار دادن میانگین به جای a کمترین مقدار خود را خواهد داشت.
فرمول ذکر شده در بالا برای محاسبه واریانس جامعه آماری به کار میرود. ولی اگر به جای جامعه آماری از یک نمونه آماری استفاده شود، ابتدا باید میانگین جامعه آماری () برآورد شود سپس واریانس نمونه برای برآورد واریانس جامعه آماری بکار رود. به این ترتیب اگر برای محاسبه واریانس نمونه، معلوم بودن میانگین نمونه را به عنوان یک محدودیت داشته باشیم، همه مقدارها به جز یکی میتوانند آزادانه تغییر کنند. زیرا تغییرات دادهها باید به شکلی باشد که میانگینشان برابر با باشد. به این ترتیب میگوئيم دادهها از n-1 درجه آزادی برخوردار هستند.
محاسبه واریانس نمونهای که نشان داده میشود، کمی با واریانس جامعه متفاوت است، زیرا در مخرج به جای n از n-1 استفاده شده است. شکل محاسباتی به صورت زیر است:
که در آن n-1 را درجه آزادی برای واریانس نمونه میگویند. اگر اندازه نمونه بزرگ شود، بین واریانس نمونه و جامعه آماری تفاوتی چندانی وجود نخواهد داشت زیرا n-1 به n نزدیک میشود.
با توجه به مثال نمرات دانشجویان، واریانس نمرات برای «مدرس الف» برابر با 3.5 و برای «مدرس ب» 21 است. اگر فرض شود که این کلاسها نمونهای از کلاسهای این دو مدرس باشند، واریانس نمونهای برای «مدرس الف» برابر با ۴ و برای «مدرس ب» ۲۴ محاسبه میشود.
نکته: اگر دادهها در مقدار ثابتی مثل b ضرب یا تقسیم شوند، واریانس آنها در b2 ضرب یا تقسیم میشود ولی تغییر مکان دادهها در میزان واریانس آنها تاثیری ندارد.
مزایا و معایب
- مزایا
- قابلیت استفاده در بیشتر مفاهیم ریاضی
- محاسبه پراکندگی حول میانگین
- نقش همه دادهها در محاسبه میزان پراکندگی
- معایب
- مربع شدن واحد اندازهگیری برای میزان پراکندگی
- تاثیر پذیری زیاد از دادههای بسیار بزرگ یا کوچک
انحراف معیار یا انحراف استاندارد
با توجه استفاده از توان ۲ در محاسبه واریانس، واحد اندازهگیری برای این شاخص به صورت مربع در خواهد آمد. برای مثال، اگر دادهها برحسب گرم باشند، واریانس برحسب گرم مربع (گرم به توان ۲) خواهد بود. این موضوع باعث میشود که نتوان واریانس را با خود دادهها مقایسه کرد.
برای رفع این مشکل کافی است که جذر واریانس را محاسبه کنیم تا واحد اندازهگیری این شاخص پراکندگی با واحد اندازهگیری دادهها یکی شود. به حاصل این کار «انحراف معیار» (Standard Deviation) میگویند. انحراف معیار جامعه آماری با و انحراف معیار نمونه S نشان داده میشود.
پس شیوه محاسباتی برای انحراف معیار به صورت زیر خواهد بود؛
در مثال نمرات دانشجویان، انحراف معیار نمرات برای «مدرس الف» برابر با 1.87 و برای «مدرس ب» 4.58 است. اگر فرض شود که این کلاسها نمونهای از کلاسهای این دو مدرس باشند، انحراف معیار نمونهای برای «مدرس الف» برابر با 2 و برای «مدرس ب» 4.9 محاسبه میشود.

نکته: اگر دادهها در مقدار ثابتی ضرب یا تقسیم شوند، انحراف معیار آنها نیز در همان مقدار ضرب یا تقسیم خواهد شد. در نتیجه تغییر مقیاس در دادهها باعث تغییر در انحراف معیار خواهد شد ولی تغییر مکان دادهها در میزان انحراف معیار آنها تاثیری ندارد.
مزایا و معایب
- مزایا
- قابلیت استفاده در بیشتر مفاهیم ریاضی
- محاسبه پراکندگی حول میانگین
- نقش همه دادهها در محاسبه میزان پراکندگی
- قابلیت استفاده در بیشتر مقایسههای آماری
- معایب
- تاثیر پذیری زیاد از دادههای بسیار بزرگ یا کوچک
- عدم ثبات در هنگام تغییر واحد دادهها
ضریب تغییرات
برای مقایسه پراکندگی دو گروه داده که با واحدهای اندازهگیری متفاوتی جمعآوری شده باشند، استفاده از انحراف معیار، واریانس، متوسط قدرمطلق انحرافات از میانگین، دامنه میان چارکی و دامنه تغییرات صحیح نیست. زیرا میدانیم که این اندازهها با تغییر مقیاس دادهها، تغییر میکنند. برای رفع این مشکل از «ضریب تغییرات» (Coefficient of Variation- CV) استفاده میشود زیرا معیاری است که میزان نسبی پراکندگی را نشان میدهد.
برای محاسبه آن کافی است که نسبت انحراف استاندارد را به میانگین بدست آورد. از آنجایی که صورت و مخرج این کسر هم واحد هستند، حاصل کسر مقداری بدون واحد است که به صورت درصدی نیز میتواند بیان شود. بنابراین ممکن است برای یک سری داده گفته شود که ضریب تغییرات ۱۵٪ است. این امر به معنی آن است که انحراف معیار ۱۵ درصد میانگین است.
محاسبه ضریب تغییرات برای جامعه آماری به شکل زیر است:
و برای نمونه آماری به صورت زیر است:
اگر در مثال نمرات دانشجویان بخواهیم اثر سختی یا سادگی آزمون (که در میزان میانگین نهفته است) را از بین ببریم و پراکندگی را برحسب میانگین هر کلاس بسنجیم، کافی است ضریب تغییر را برای هر یک محاسبه کنیم. مدرسی که دارای ضریب تغییرات کمتری است، نمرههای یکدست و همگنی داشته.
به این ترتیب ضریب تغییرات برای «مدرس الف» برابر با 12.47٪ و برای «مدرس ب» 30.55٪ است. اگر فرض شود که این کلاسها نمونهای از کلاسهای این دو مدرس باشند، ضریب تغییرات نمونهای برای «مدرس الف» برابر با 13.33٪ و برای «مدرس ب» 32.66٪ محاسبه میشود.

نکته: اگر دادهها در مقدار ثابتی ضرب یا تقسیم شوند، ضریب تغییرات برای آنها تغییر نخواهد کرد، در نتیجه تغییر مقیاس در دادهها تاثیری روی ضریب تغییرات ندارد.
باید توجه داشت که برای محاسبه ضریب تغییرات لازم است دادهها کمی و از نوع نسبی باشند. محاسبه ضریب تغییرات برای دادههای فاصلهای صحیح نیست.
مثال
دمای متوسط دو شهر در طول ۵ روز از سال برحسب سانتیگراد و فارنهایت در جدول زیر آورده شده است.
| دمای شهرها | روز اول | روز دوم | روز سوم | روز چهارم | روز پنجم | میانگین | انحراف معیار | ضریب تغییرات |
| الف (سانتیگراد) | 0 | 10 | 20 | 30 | 40 | 20 | 15.81 | 0.79 |
| ب (فارنهایت) | 32 | 50 | 68 | 86 | 10 | 68 | 28.46 | 0.42 |
با توجه به تفاوت واحد اندازهگیری دما در این دو شهر برای مقایسه میزان پراکندگی شاید ضریب تغییرات مناسب به نظر برسد. همانطور که دیده میشود «شهر ب» دارای ضریب تغییرات بیشتری است پس احتمال دارد این طور تصور شود که دما در آن به نسبت میانگین تغییرات زیادی دارد. ولی با توجه به اینکه دما با واحد سانتیگراد یا فارنهایت یک کمیت از نوع فاصلهای است، استفاده از CV در اینجا صحیح نیست. (کمیت فاصلهای، کمیتی است که در آن صفر به صورت قراردادی در نظر گرفته میشود و به معنی هیچ نیست.)
اگر به جای سانتیگراد و فارنهایت از واحد کلوین برای دمای این دو شهر استفاده شود جدول زیر حاصل میشود. (برای تبدیل دمای سانتیگراد به کلوین مقدار 273.5 باید به همه دادهها اضافه شود. همچنین برای تبدیل فارنهایت به کلوین نیز دما برحسب فارنهایت را با 459.67 جمع کرده و نتیجه را به 1.8 تقسیم میکنیم.)
| دمای شهرها (کلوین) | روز اول | روز دوم | روز سوم | روز چهارم | روز پنجم | میانگین | انحراف معیار | ضریب تغییرات |
| الف | 273.5 | 283.5 | 293.5 | 303.5 | 313.5 | 293.5 | 15.81 | 0.054 |
| ب | 273.15 | 283.15 | 293.15 | 303.15 | 313.15 | 293.15 | 15.81 | 0.054 |
طبق این جدول دیده میشود که تغییرات دما نسبت به میانگین که همان ضریب تغییرات است، در «شهر الف» و «شهر ب» تقریبا یکسان است.
مزایا و معایب
- مزایا
- نقش همه دادهها در محاسبه میزان پراکندگی
- ثبات در هنگام تغییر واحد دادهها
- امکان مقایسه بین دو گروه از دادهها با واحدهای متفاوت
- معایب
- تاثیر پذیری زیاد از دادههای بسیار بزرگ یا کوچک
- پیچیدگی و طولانی بودن محاسبه
- عدم قابلیت محاسبه برای دادههای منفی
- نامعتبر شدن مقدار ضریب تغییرات زمانی که میانگین به سمت صفر نزدیک شود













ناپایدارترین اندازه پراکندگی رو کدوم یکی داره
با سلام خدمت شما؛
ضعیفترین و غیر قابل اطمینانترین روش اندازهگیری پراکندگی دادهها بین این چند مورد، محاسبه دامنه تغییرات یا Range است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
با سلام؛ چرا در محاسبه واریانس نمونه، تو مخرج از n یک واحد کم میکنیم؟
سلام خیلی ممنون از زحمتی که کشیدین. میخواستم بگم برای مدرس الف، چارک سوم میشه 16.5 و چارک اول میشه 13.5 بنابراین IQR میشه 3. لطفا برای جلوگیری از گیج شدن خواننده های وبسایت، هر چه زودتر درستش کنین. خیلی ممنون.
با سلام،
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
خیلی عالی بود ممنون
سلام
سپاس از توضیحات جامع و کاملتون
با سلام واریانس اعداد k+1,…3,2,1 چی میشه
باعرض سلام ودرود خدمت شما
خیلی خیلی ممنون بابت مطالب فوق العادتون
البته بیشتر مطالب برای من خیلی تخصصی محسوب میشدن و بیشتر از کلیات آموزشتون بهره بردم.
اگه امکان داره پاسخ این دوتا سوال رو بهم بدید
۱-میانگین وانحراف معیار قدنوزادان یک شهرستان در بدو تولدبه ترتیب ۵۰ و۱/۵سانتی متر بوداگر توزیع قد نرمال باشدچند درصد از نوزادان قد بین ۴۷تا۵۳ سانتی متر دارند؟
۲_طول مدت بیماری چه نوع متغیری است؟۱.کمی فاصله ای
۲.کیفی رتبه ای
۳.کیفی اسمی
۴.کمی نسبی
سلام در فرمول محاسبه واریانس نمونهای بجای x باید از xبار استفاد بشه.
همچنین در ویدئو مربوطه
با سپاس
سلام.
فرمول صحیح نوشته شده، اما به دلیل کوچک بودن فونت خط روی x قابل مشاهده نبود که مورد بازبینی قرار گرفت و اکنون قابل مشاهده است.
سپاس از همراهی و بازخوردتان.
با عرض سلام. جسارتا جهت مقایسه دو گروه عددی آیا میتوان نسبت میانگین به انحراف معیار هر گروه را بعنوان شاخص آن گروه ( نشان دهنده تمامی خواص اعداد زیر گروه ) معرفی کرد؟ یا فرمول کاملتری برای نماینده گروه وجود دارد؟ ممنون
واقعاعالی??
درود بر شما همراه مجله فرادرس،
برای آنکه امکان مقایسه دو جامعه یا دو مقدار شاخص میسر شود، باید واحد اندازه گیری را از بین ببریم. به این منظور در آمار، ضریب تغییرات یا CV مطرح و به کار برده میشود. همانطور که در متن نیز خواندید، CV همان خارج قسمت تقسیم انحراف معیار بر میانگین است. (برعکس فرمولی ارائه شده شما) البته روش شما هم قابل استفاده است و از آن نسبت هم برای مقایسه استفاده میکنند. البته فرمول کاملتر در این حوزه میتواند برای مقایسه همه مشاهدات، استفاده از امتیاز z یا zscore باشد که هر مشاهده را استاندارد کرده که در نتیجه مشاهدات نیز قابل مقایسه میشوند.
پیروز و تندرست باشید.
سلام و عرض ادب
ذکر شدن شاخص های پراکندگی در کنار شاخص های تمایل مرکزی چه کمکی به محققین میکند؟
و برای مثال ۳±۲۵ به چه معنی می باشد؟
سلام و درود بر شما خواننده گرامی،
پرسش شما بسیار سوال مهمی است. همانطور که میدانید، دادههای بخصوص مقادیر کمی، دارای واحد اندازهگیری هستند. برای مثال ممکن است اطلاعات جمعاوری شده براساس وزن (با واحد کیلوگرم) باشند. از طرفی میانگین نیز یک معیار تمرکز است که با واحد خود دادهها یکسان است. برای مثال میانگین نیز با واحد کیلوگرم مشخص میشود. از طرفی به جز واریانس (که با واحد مربع مشخص میشود) بسیاری از شاخصهای پراکندگی (مانند انحراف معیار) با واحد دادهها یکی هستند. بنابراین امکان جمع یا تفریق و محاسبات شاخصهای مرکزی و پراکندگی میسر است.
در پرسش شما که به صورت ۲۵+۳ و ۲۵-۳ نوشته شده، مقدار اول نشانگر میانگین است و دومین عدد نیز نشانگر پراکندگی (مثلا انحراف معیار) است. پس میتوان گفت که برای مثال شما بستهها به طور میانگین ۲۵ کیلو وزن داشته و ۳ کیلوگرم اختلاف یا انحراف از میانگین تغییر میکند. یعنی بعضی از آنها ممکن است ۲۸ و بعضی دیگر نیز ۲۲ کیلوگرم وزن دارند. ولی مقادیر نزدیک به این دو عدد کمتر از مقادیری است که به ۲۵ نزدیک هستند. این موضوع نقش میانگین و انحراف معیار را نشان میدهد.
بهتر است مطلب دیگری با عنوان واریانس و انحراف معیار | به زبان ساده
از این که سوالاتتان را با ما در میان میگذارید، سپاسگزاریم.
تندرست و پیروز باشید.
سلام
در محاسبه واریانس اگر m داده وابسته به هم باشند، واریانس پگونه تغییر میکند؟
ایا فرمول همان فرمول قبلیست؟
سلام احسان خان؛
فرمول های گفته شده مربوط به مشاهدات مستقل است. زمانی که با متغیرهای همبسته مواجه هستیم، واریانس مجموع با مجموع واریانسها برابر نیست. برای اطلاع بیشتر از نحوه محاسبه واریانس برای چنین حالتی بهتر است نوشتار کوواریانس و نحوه محاسبه آن — به زبان ساده را مطالعه کنید.
به هر حال نحوه محاسبه واریانس برای این حالت به صورت مجموع واریانسها و جمع با مجموع کوواریانس ها خواهد بود.
Var(X+Y)=Var(X)+Var(Y)+Cov(X,Y)
تندرست و پیروز باشید.
با سلام خدمت شما
نوشته بودید برای محاسبه انتگرال نیاز به تعریف واریانس داریم ولی محاسبه انتگرال قدر مطلق هم پیچیده نیست آیا دلیل دیگری برای محاسبه واریانس داریم؟ با سپاس از شما
سلام و درود به شما همراه مجله فرادرس!
محاسبات انتگرال و مشتق توابع درجه دو که در همه نقاط مشتقپذیر و انتگرال پذیر هستند نسبت به تابع قدر مطلق بسیار سادهتر است. ولی در مورد »برای محاسبه انتگرال نیاز به تعریف واریانس داریم» چیزی در مطلب نوشته نشده است.
از اینکه همواره همراه مجله فرادرس هستید بسیار خرسندیم.
موفق و شاد و تندرست باشید.
سلام
MD برای مدرس الف فکر کنم ۱.۲۵ میشه نه ۱.۵
درست میگم؟
سلام و درود
از اینکه خواننده مطالب مجله فرادرس هستید، سپاسگزاریم.
با توجه به شیوه محاسبه و فرمول گفته شده، مقدار MD برای مدرس الف همان ۱٫۵ خواهد بود. همانطور که دیدید، میانگین برای نمره این ۸ دانشجو برابر با ۱۵ است. مجموع قدر مطلق اختلافات نسبت به میانگین هم ۱۲ شده و با تقسیم این عدد بر ۸، حاصل ۱٫۵ خواهد بود.
باز هم از همراهی شما با فرادرس، قدردانی میکنیم.
پیروز و سربلند باشید.
سلام متشکر از آموزش شما
فقط من در بخش دامنه میان چارکی متوجه عدد 4.25 نمی شوم
با خواندن قسمت چارک ها و چندین بار محاسبه برای نمرات الف مقدار 3 را بدست می آورم. ولی شما فرمودید 4.25 می شود محاسبات خودتان را ارائه دهید .متشکر
منم ۳ درمیارم پنجاه بارم امتحان کردم
۱۳.۵ و ۱۶.۵ میشه
سلام و وقت بخیر؛
از اینکه همراه فرادرس هستید، بسیار سپاسگزاریم.
همانطور که فرمودید، محاسبه چارک اول و سوم برای مدرس الف به اشتباه نوشته شده است. مقدار صحیح برای دامنه میان چارکی مقدار ۲ است زیرا چارک اول برابر با ۱۴ و چارک سوم نیز ۱۶ است که تفاضل آنها برابر با ۲ خواهد بود.
موفق و پیروز و سربلند باشید.
سلام ما چند فروشگاه داریم که طی شش ماه و در هر ماه مبالغ فروش متفاوتی داشته اند ، اگه بخواهیم بی ثبات ترین فروشگاه در میزان فروش را پیدا کنیم باید از کدوم روش استفاده کرد ؟ ممنون از راهنمایی تون
سلام و با تشکر از توجه شما به مطالب فرادرس
همانطور که گفته شد ضریب تغییرات میتواند بدون توجه به واحد اندازهگیری (میزان فروش) وضعیت پراکندگی مقادیر را نشان دهد. بنابراین از آنجایی که مقادیر فروش منفی نیستند ضریب تغییرات مناسب است. هر چه ضریب تغییرات کمتر باشد، به معنی ثابت بودن تغییرات و همگن بودن میزان فروش است.
سپاس از اینکه همراه فرادرس هستید.
با درود.
در قسمت معایب ضریب تغییرات نوشته شده عدم قابلیت محاسبه برای داده های نامنفی،در صورتی که باید داده های منفی باشه.
سلام و سپاس بابت توجهتان به مطالب فرادرس
حق با شما است. برای مقادیر منفی ضریب تغییرات قابل محاسبه نیست.
منتظر نظرات سازنده شما هستیم.
با سلام و تشکر از توجه شما به مطالب فرادرس
کاملا حق با شما است. ضریب تغییرات برای مقادیر منفی قابل محاسبه نیست!
باز هم از اینکه همراه فرادرس هستید متشکریم.