آشنایی با WinBUGS به کمک R — راهنمای کاربردی

۶۴۰ بازدید

آخرین به‌روزرسانی: ۸ خرداد ۱۴۰۲

زمان مطالعه: ۱۱ دقیقه

دانلود PDF مقاله

آشنایی با WinBUGS به کمک R — راهنمای کاربردی

نرم‌افزار WinBUGS یک بسته محاسبات آماری برای تحلیل بیزی با استفاده زنجیره مارکف مونت کارلو است که قابلیت اجرا در زبان برنامه‌نویسی R را داراست. از آنجایی آشنایی با WinBUGS در حل بسیاری از تحلیل‌های آماری به کار می‌آید، آگاهی از نحوه استفاده از آن برای بسیاری از «تحلیل‌گران داده» ضروری است.

فهرست مطالب این نوشته

آشنایی با WinBUGS

WinBUGS از دستورات و کدهای BUGS استفاده می‌کند. زبان دستوری BUGS در حقیقت یک پروژه نرم‌افزاری برای انجام محاسبات آماری در استنباط بیزی به کمک نمونه‌گیری گیبز و MCMC محسوب شده که توسط دانشگاه کمبریج در بخش «آمار حیاتی» (Bioinformatic) تولید و توسعه یافته است. به این ترتیب مشخص است که BUGS از سر کلمه‌های Baysian inference Using Gibbs Sampling تشکیل شده.

به منظور استفاده از WinBUGS می‌توانید از محیط برنامه‌نویسی R استفاده کنید و کدهای برنامه را به شکل BUGS و در یک فایل متنی بنویسید. دیگر بسته‌های محاسبات آمار بیزی مانند OpenBUGS نیز کد نویسی مشابه WinBUGS دارند. برای دریافت نرم‌افزار WinBUGS از (+) استفاده کنید. OpenBUGS نسخه متن-باز WinBUGS است در نتیجه دسترسی به کد برنامه‌ها و دستورات در این نسخه وجود دارد.

از آنجایی که در بسته WinBUGS با مفاهیم آمار بیز و توزیع پسین و پیشین و همچنین شبیه‌سازی مونت کارلو زنجیره مارکف (MCMC) سر و کار خواهیم داشت بهتر است مطالب قضیه بیز در احتمال شرطی و کاربردهای آن، احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده و شبیه سازی مونت کارلو (Monte Carlo Simulation) – محاسبه انتگرال‌ به روش عددی را بخوانید. همچنین مطالعه نوشتار یادگیری ماشین به زبان قضیه بیز، بی نظمی شانون و فلسفه نیز خالی از لطف نیست.

آشنایی با WinBUGS

یکی از روش‌های پیاده‌سازی آمار بیزی با استفاده از زنجیره مارکوف مونت کارلو، بسته محاسباتی WinBUGS است. این بسته محاسباتی قابلیت انعطاف‌پذیری زیادی نسبت به دیگر بسته‌های محاسبات و استنباط آماری در R دارد. ولی به هر حال به علت پیچیدگی محاسبات از لحاظ هزینه محاسبه، گران قیمت است. معمولا دستوراتی که برای تحلیل مدل لازم دارید با استفاده از کدهای BUGS در یک فایل متنی ذخیره کرده و با نصب WinBUGS در R قادر به اجرای آن‌ها هستید.

فیلم آموزش تحلیل های بیزی با نرم افزار وین باگز WinBUGS در فرادرس

کلیک کنید

هنگامی که می‌خواهید کدهایی برای WinBUGS بنویسید باید نکاتی که در ادامه فهرست شده‌اند را در نظر بگیرید.

مدل‌ها در WinBUGS در دو بخش نوشته می‌شود. بخش اول مربوط به توزیع تصادفی داده‌ها و بخش تصادفی مدل است و بخش دوم نیز مربوط به تابع مدل خطی به منظور برآورد پارامترهای مدل است.
تا این تاریخ محاسبات برداری برای مدل‌ها در WinBUGS طراحی نشده است و باید این گونه محاسبات بوسیله حلقه تکرار نوشته و پیاده‌سازی شوند.
با توجه به بند شماره ۲، اندیس‌ گذاری برای بردارها بسیار امر مهم و اساسی محسوب می‌شود. در نتیجه به تفاوت بین [mu[i و mu دقت کنید.
واریانس معمولا توسط میزان دقت در نظر گرفته شده و به صورت tau نمایش داده می‌شود و داریم $tau=\frac{1}{variance}$ .
محاسبات باید در خط فرمان‌های جداگانه نوشته شود و ممکن است بعضی از توابع به شیوه محاسبات در R صورت نگیرد. برای مثال برای توان رساندن باید از فرمان (power(x,2 به جای x^2 استفاده شود.
ترتیب عبارت‌ها مهم نیست. بنابراین ممکن است مقدار دهی به یک متغیر قبل از تعریف متغیر صورت گیرد.
گره یا نود (node) تصادفی به صورت ‍~ و گره‌های قطعی به شکل -> در کد ظاهر می‌شوند. در اینجا منظور از گره رابطه‌ای است که وظیفه آن نسبت دادن طرف راست به چپ رابطه است.

به کارگیری WinBUGS به کمک R

به منظور آشنایی با تفاوت‌های ذکر شده در بالا، در ادامه به بررسی یک روند مدل سازی خط (رگرسیون خطی ساده-lm) با استفاده از دستورات R و WinBUGS خواهیم پرداخت.

آماده سازی محیط کار برای WinBUGS

بسته R2WinBUGS برای اجرای کدهای WinBUGS در محیط R لازم است. از طرفی بسته mcmcplots نیز به منظور رسم نمودارهای مربوط به زنجیره مارکف مونت کارلو ضروری به نظر می‌رسد. به کمک کدهای زیر در R آن‌ها را فراخوانی می‌کنیم.

1#Import required packages
2library(R2WinBUGS)
3library(mcmcplots)

نکته: قبل از بارگذاری این بسته‌ها باید ابتدا آن‌ها را به استفاده از دستور Install.package روی R نصب کنید. برای مثال کافی است یکبار دستورات زیر را اجرا کنید تا عمل نصب این بسته‌ها روی R صورت بگیرد.

1install.packages("R2WinBUGS")
2install.packages("mcmcplots")

آماده سازی داده‌ها

در این مثال، از مجموعه داده iris که مربوط به سه نوع گل و اندازه کاسبرگ و گلبرگ آن‌ها است، استفاده خواهیم کرد. ۱۵۰ مشاهده در این مجموعه داده وجود داشته که از هر گونه، ویژگی‌های ۵۰ نمونه ثبت شده است.

فیلم آموزش نمونه گیری در نرم افزار آر R در فرادرس

کلیک کنید

کد زیر به منظور فراخوانی این مجموعه داده در R تهیه شده است. البته با اجرای کد زیر، آمارهای توصیفی و نمودار مربوط به آن‌ها نیز ظاهر خواهد شد.

1data(iris)
2summary(iris)
3#Plot the raw data
4plot(iris$Sepal.Length ~ iris$Petal.Length, xlab = "Petal length", ylab="Sepal length")

همانطور که گفته شد، خروجی‌ها به صورت زیر خواهند بود که شامل خلاصه‌ای از آمارهای توصیفی و نمودار پراکندگی داده‌ها مربوط به طول کاسبرگ و گلبرگ است.

1 Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
2 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
3 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
4 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
5 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
6 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
7 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500

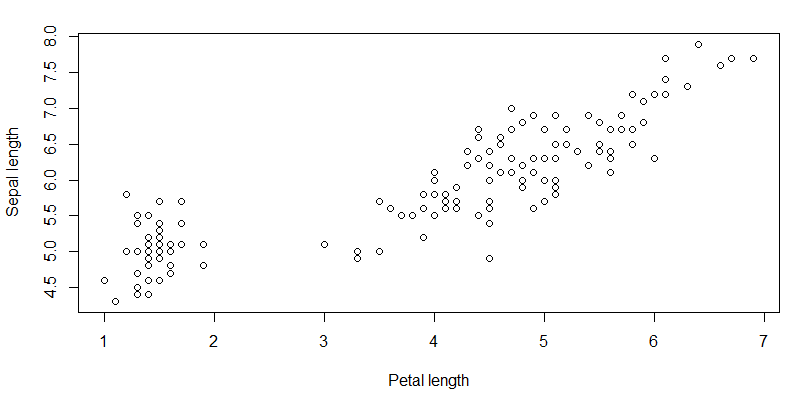
از آنجایی که WinBUGS قادر به تشخیص و به کارگیری «چارچوب داده» (Dataframe) نیست، باید هر بُعد از این مجموعه داده را در متغیر جداگانه‌ای بمنظور به کارگیری در WinBUGS قرار داد. این کار در کد زیر صورت گرفته است.

1sepal <- iris$Sepal.Length
2petal <- iris$Petal.Length

بعد از تعریف این دو متغیر بهتر است عمل استاندارسازی را برای آن‌ها به کار برده تا بدون مقیاس باشند. بهتر است همیشه هنگام مدل‌سازی بوسیله WinBUGS و حتی دستورات و یا بسته‌های دیگر، عمل استاندارسازی داده‌ها را انجام دهید. این کار را به کمک تابع scale انجام خواهیم داد. برای مثال اگر قرار است متغیر sepal استاندارد شود از دستور زیر کمک می‌گیریم. البته از آنجایی که در مجموعه داده iris طول و عرض کاسبرگ‌ها دارای یک مقیاس هستند در این مرحله نیازی به انجام این کار نیست.

1sepal <- as.numeric(scale(iris$Sepal.Length))

معرفی مدل

احتمالا با دستور $lm$ که مخفف Linear Model است، برای ایجاد یک مدل خطی در R آشنایی دارید. فرض کنید قرار است یک مدل خطی (رگرسیون خطی) براساس طول کاسبرگ‌ها (Sepal) و ارتباطشان با گلبرگ‌ها (Petal) ایجاد کنیم. کد زیر به این منظور نوشته شده است.

1lm1 <- lm(sepal ~ petal)
2summary(lm1)

خروجی این مدل رگرسیونی به صورت زیر خواهد بود. همانطور که می‌دانید Intercept عرض از مبدا و petal ضریب یا شیب خط مورد نظر را نشان می‌دهد. به این ترتیب می‌توانیم رابطه خطی را به صورت $sepal=4.3066+petal\times 0.40892$ نوشت. از این مدل برای پیش‌بینی sepal (طول گلبرگ) یک گل برحسب petal (کاسبرگ) بهره خواهیم برد.

1Call:
2lm(formula = sepal ~ petal)
3
4Residuals:
5     Min       1Q   Median       3Q      Max 
6-1.24675 -0.29657 -0.01515  0.27676  1.00269 
7
8Coefficients:
9            Estimate Std. Error t value Pr(>|t|)    
10(Intercept)  4.30660    0.07839   54.94   <2e-16 ***
11petal        0.40892    0.01889   21.65   <2e-16 ***
12---
13Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
14
15Residual standard error: 0.4071 on 148 degrees of freedom
16Multiple R-squared:   0.76,	Adjusted R-squared:  0.7583 
17F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

ولی در WinBUGS برای انجام این عملیات، مقداری کدها پیچیده‌تر هستند. به این معنی که با توجه به توزیع پیشین و استنباط بیزی، باید توزیع احتمالی برای متغیر و همینطور توزیع پیشین را برای هر پارامتر مدل مشخص کنیم. در مثال ما فرض بر این است که هیچ پیش‌فرضی برای توزیع پارامترها و یا اطلاع از نوع وابستگی بین اندازه کاسبرگ و گلبرگ از قبل وجود ندارد. به این ترتیب باید از پیشین «ناآگاهنده» (Uninformative) استفاده شود. توزیع یکنواخت و توزیع نرمال با واریانس بزرگ از انواع توزیع‌های ناآگاهنده هستند.

از آنجایی که ترتیب کدها در WinBUGS‌ اهمیت ندارد بهتر است برنامه را به دو بخش تقسیم کنیم. بخش اول به منظور تعیین «تابع درستنمایی» (Likelihood Function) به کار رود و بخش دیگر برای تعریف توزیع پیشین تهیه شود. دو خط اول از کدی که در ادامه مشاهده می‌کنید به منظور ایجاد فایل متنی به نام mod1.txt است که کدهای WinBUGS در آن نوشته خواهد شد. در انتها نیز با استفاده از دستور ()sink این فایل بسته شده و دستورات داخل آن ثبت می‌شوند.

1sink("mod1.txt")        
2cat("
3#...

در قسمت بعدی تابع درستنمایی برای مدل مورد نظر معرفی می‌شود. منظور از مدل در اینجا همان مفهوم مدل خطی است که توسط تابع $lm$ در R معرفی شد ولی با این تفاوت که با توجه به توضیحات قبلی، ساختار ایجاد مدل در دو بخش صورت خواهد گرفت. فرض کنید که داده‌های نمونه از جامعه‌ای با توزیع نرمال با میانگین mu و دقت tau تهیه شده باشند. از طرفی پارامترهای مدل خطی نیز عرض از مبدا alpha و شیب beta در نظر گرفته شده است. کدی که در ادامه مشاهده می‌کنید به منظور تعریف چنین مدلی به کار رفته است. همانطور که مشخص است به علت عدم امکان استفاده از محاسبات برداری، نمونه‌ها یک به یک و به تعداد N تولید شده‌اند. میانگین توزیع نرمال برای داده‌ها نیز از مدل خطی استخراج شده است. همانطور که می‌بینید استفاده از [mu[i قبل از تعریف آن توسط رابطه مدل خطی، صورت گرفته است.

1#...
2MODEL LR1 {
3    for(i in 1:N) {
4    sepal[i] ~ dnorm(mu[i], tau)
5      mu[i] <- alpha + beta*petal[i]
6}
7#...

گام بعدی، تعریف توزیع پیشین برای پارامترهای مدل قبلی یعنی mu alpha و beta‌ است. همانطور که در قبل گفته شد، فرض شده که هیچ اطلاع قبلی از توزیع این پارامترها در اختیار ما نیست. بنابراین برای عرض از مبدا توزیع را نرمال با میانگین صفر و دقت (Precision) کوچک (واریانس بزرگ) در نظر می‌گیریم. به این ترتیب به نظر می‌رسد که اطلاع زیادی از مقدارهای آن در اختیار نباشد. برای تابع توزیع پیشین پارامتر tau نیز توزیع یکنواخت در بازه صفر تا ۱۰ را انتخاب می‌کنیم تا مثبت بودن واریانس sigma را مشخص و قطعی کرده، به طور یکنواخت مقدارهای در این بازه را به آن اختصاص دهیم. به این ترتیب به نظر می‌رسد که دقت هم در بازه $(0,10)$ تغییر خواهد کرد.

1#...
2alpha ~ dnorm(0,0.001)
3beta ~ dnorm(0,0.001)
4
5tau <- pow(sigma, -2)
6sigma ~ dunif(0,10) 
7#...

با در نظر گرفتن کدهای نوشته شده در بالا، به نظر می‌رسد که تعریف مدل کامل شده و می‌توانیم به ثبت کدها در فایل متنی پایان دهیم. برای این کار کافی است که کدهای زیر را در انتهای برنامه قرار دهیم.

1#...
2}
3", fill = TRUE)
4sink()

تعریف داده‌ها، پارامترها و تنظیمات

بعد از آنکه کدها برای ایجاد مدل در WinBUGS آماده شد، زمان تنظیمات پارامترها برای اجرای مدل فرا می‌رسد. این کار را طی گام‌های زیر انجام می‌دهیم. این گام‌ها در حقیقت بخش دوم از کدهای تحلیلی توسط WinBUGS را تشکیل می‌دهد.

ارسال داده‌های مربوط به کاسبرگ و گلبرگ به مدل
تعیین پارامترهایی که باید برآورد و گزارش شوند.
مقدار دهی اولیه به پارامترهای مدل.
استفاده از MCMC و تعیین پارامترهای آن.

به این ترتیب در گام اول، داده‌ها را فراخوانی می‌کنیم. همه متغیرها باید در یک لیست معرفی شوند. توجه داشته باشید که تعداد مشاهدات مورد نظر باید به عنوان یک مقدار در این لیست وجود داشته باشد تا WinBUGS بتواند عملیات را به درستی انجام دهد. در اینجا تعداد مشاهدات مورد استفاده در مدل را با $N$ نشان داده‌ایم. به کد زیر توجه کنید.

1N = length(sepal)
2data = list("N","sepal","petal")

در ادامه و گام دوم نیز پارامترهایی که باید مورد محاسبه قرار گرفته و در خروجی ظاهر شوند را در متغیر params به عنوان یک بردار قرار داده‌ایم. توجه داشته باشید که فقط پارامترهای alpha و beta که به عنوان عرض از مبدا و شیب خط در نظر گرفته شده بودند، مورد نظر است و پارامتر tau ذکر نشده است. دستور زیر به این منظور نوشته شده.

1params = c("alpha", "beta")

مقدار دهی اولیه نیز به عنوان گام سوم، باید صورت گیرد. هر چند WinBUGS قادر است به طور خودکار مقدار دهی اولیه را بخصوص برای MCMC انجام دهد ولی بهتر است با توجه به حدسی که شما برای پارامترهای مدل دارید، این کار را به صورت دستی انجام داده تا سرعت انجام محاسبات بیشتر و زمان اجرای برآورد پارامترهای مدل کوتاه‌تر شود. این کار را توسط یک تابع به نام inits انجام داده‌ و پارامترهای اولیه را مشخص کرده‌ایم. در کد زیر می بینید که پارامترهای alpha و beta براساس یک مقدار تصادفی از توزیع نرمال انتخاب شده‌اند ولی برای sigma که نمایانگر واریانس است، از مقدار ۱ استفاده شده که مثبت بودن واریانس را تضمین کند. به این ترتیب توزیع پیشین پارامترها تعیین می‌شود.

1inits <- function () {list(alpha = rnorm(1),
2                           beta = rnorm(1),
3                           sigma = 1)}

در گام آخر نیز تنظیمات MCMC را انجام می‌دهیم. بهتر است اگر از عملکرد مدل به شکل کامل اطلاع ندارید، مدل را به واسطه داده‌های محدود اجرا کنید تا اگر مشکلی در برنامه یا مدل‌سازی وجود دارد در زمان کوتاه مشخص شده و خطاها مرتفع گردند سپس با همه مشاهدات پارامترهای مدل را برآورد کنید. در ادامه تعداد زنجیره‌های مارکف nc=3 انتخاب شده. از طرفی تعداد نمونه‌ها برای هر زنجیره نیز ni=5000 داده در نظر گرفته شده است. همچنین تعداد نمونه‌هایی که در فرایند MCMC می‌تواند کنار گذاشته شود در nb=1000 مشخص شده است. میزان ارتباط و همبستگی بین مشاهدات نیز در nt=1 مشخص شده است به این معنی که وابستگی بین هر مشاهده با مشاهده بعدی برقرار است. اگر مقدار nt را افزایش دهید، میزان «خودهمبستگی» (Autocorrelation) کاهش می‌یابد. این پارامترهای برای اجرای الگوریتم MCMC لازم است.

اجرای مدل BUGS

به منظور اجرای مدل باید از تابع bugs در R، به همراه پارامترهای مربوط به داده‌ها و مقدارهای اولیه و پارامترهای MCMC که در بخش قبلی ایجاد کردید، استفاده کنید. با اجرای این دستور، پنجره نرم‌افزار WinBUGS باز خواهد شد. البته اگر در تابع bugs پارامتر debug=FALSE باشد، بعد از اجرای مدل و محاسبه پارامترها، این پنجره بسته شده و به پنجره R بازخواهید گشت. البته برای آنکه از خطاهای احتمالی آگاه شوید بهتر است که این پارامتر را به صورت debug=TRUE در تابع به کار ببرید.

فیلم آموزش تحلیل شبکه های اجتماعی با زبان R و متن کاوی Text Mining در فرادرس

کلیک کنید

توجه داشته باشید، مسیری که مربوط به فایل‌ متنی مدل در بخش model.file به درستی در قسمت working.directory وارد کنید، اگر این کار را انجام نداده باشید، مسیر جاری در R به کار گرفته خواهد شد. همچنین محل نصب برنامه WinBUGS را نیز در بخش bug.directory باید تعیین کنید. معمولا محمل نصب این برنامه در مسیر C:\\Program Files\\WinBUGS14 است.

1bugs.out <- bugs(data=data, inits=inits, parameters.to.save=params, model.file="mod1.txt", 
2 n.chains=nc, n.iter=ni, n.burnin=nb, n.thin=nt, debug=TRUE, DIC=TRUE, bugs.directory = "C:\\Program Files\\WinBUGS14", working.directory=getwd())

محاسبات MCMC و نمایش خروجی‌ها

برای نمایش خروجی‌ها و نمودارها، می‌توانید هم از برنامه R استفاده کنید و هم از WinBUGS کمک بگیرید. فقط توجه داشته باشید که برای نمایش نتایج در برنامه R باید از WinBUGS خارج شوید.

فیلم مجموعه آموزش برنامه نویسی آر R و RStudio – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای مدل و پارامترهای آن کافی است از دستورات زیر استفاده کنید.

1print(bugs.out, digits = 3)
2bugs.summary <- bugs.out$summary
3bugs.DIC <- bugs.out$DIC

خط دوم و سوم نیز برای نمایش بخشی از خروجی به کار رفته است. به این ترتیب فقط خلاصه (summary) و «معیار انحراف اطلاعات» (Deviance Information Criterion- DIC) نمایش داده خواهند شد. همچنین نمودارهای و خروجی را به کمک دستورات زیر نیز می‌توانید در R‌ نمایش دهید.

1plot(bugs.out) # gives a summary plot of coefficients and credible intervals
2mcmcplot(bugs.out) # opens up a new window with a set of plots to evaluate mcmc chain convergence

به هر حال خروجی‌های مربوط به نرم‌افزار R به صورت زیر ظاهر می‌شوند.

1Inference for Bugs model at "mod1.txt", fit using WinBUGS,
2 3 chains, each with 5000 iterations (first 1000 discarded)
3 n.sims = 12000 iterations saved
4            mean    sd    2.5%     25%     50%     75%   97.5%  Rhat n.eff
5alpha      4.306 0.080   4.153   4.252   4.306   4.360   4.462 1.001 12000
6beta       0.409 0.019   0.371   0.396   0.409   0.422   0.446 1.001 12000
7deviance 157.106 2.487 154.300 155.300 156.500 158.200 163.500 1.002  3000
8
9For each parameter, n.eff is a crude measure of effective sample size,
10and Rhat is the potential scale reduction factor (at convergence, Rhat=1).
11
12DIC info (using the rule, pD = Dbar-Dhat)
13pD = 3.0 and DIC = 160.1
14DIC is an estimate of expected predictive error (lower deviance is better).

و نمودارها نیز در محیط مرورگر اینترنت مطابق با تصویرهای زیر خواهند بود.

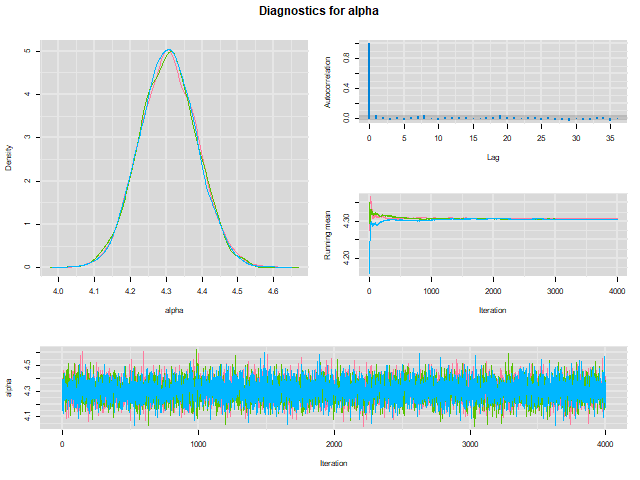
alpha winbugs plot

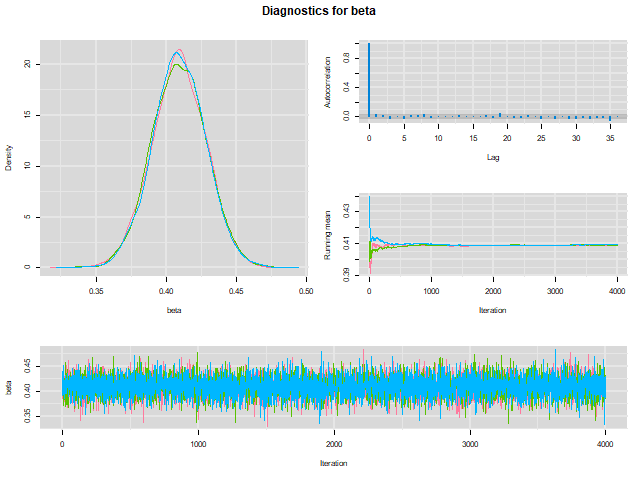
beta winbugs plot

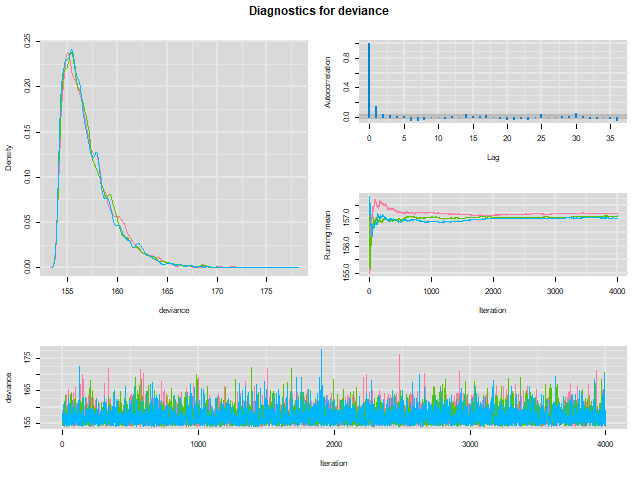
deviance winbugs plot

همانطور که مشخص است، همگرایی به مقدار 4.306 برای alpha و 0.409 برای beta توسط نمودارها مشهود است. البته خروجی‌ها و نمودارها نیز در پنجره WinBUGS به شکل زیر خواهند بود.

1Node statistics
2	 node	 mean	 sd	 MC error	2.5%	median	97.5%	start	sample
3	alpha	4.306	0.07952	7.737E-4	4.153	4.306	4.462	1001	12000
4	beta	0.4091	0.01915	1.885E-4	0.3714	0.4091	0.4464	1001	12000
5	deviance	157.1	2.487	0.02616	154.3	156.5	163.5	1001	12000
6dic.stats()
7
8DIC
9Dbar = post.mean of -2logL; Dhat = -2LogL at post.mean of stochastic nodes
10	Dbar	Dhat	pD	DIC	
11sepal	157.106	154.109	2.997	160.103	
12total	157.106	154.109	2.997	160.103

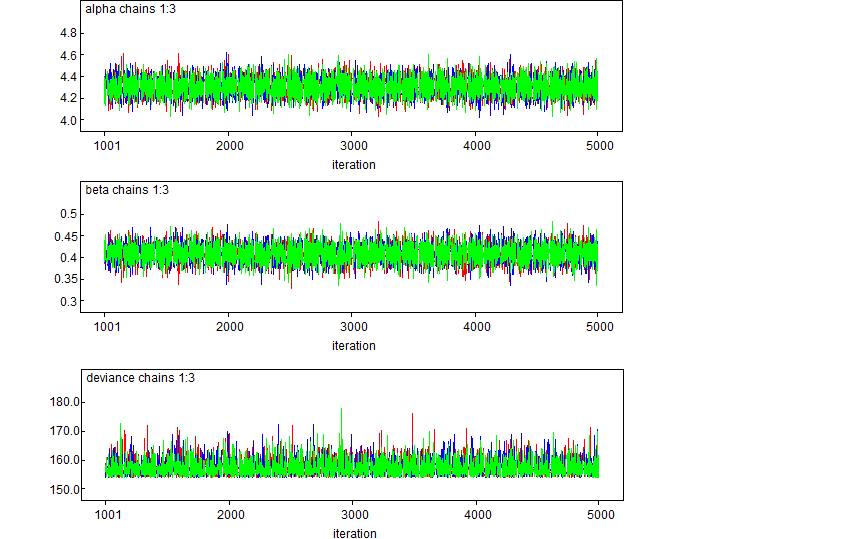
WinBUGS mcmc plots

می‌توانید این نتایج و پارامترهای مدل را با مدلی که توسط دستور lm در R اجرا کردید مقایسه کنید. مشخص است که پارامترهای مدل در هر دو حالت بسیار نزدیک هستند. برای مثال پارامتر عرض از مبدا alpha در حالتی که از مدل رگرسیون خطی استفاده کردید برابر با 4.306 بدست آمد و در مدل WinBUGS به کمک MCMC نیز این پارامتر برابر با 4.306 است. همچنین برای شیب خط یا ضریب کاسبرگ (Petal) نیز مقدار beta= 0.4091 و به کمک مدل رگرسیونی نیز 0.4089 حاصل شده است که اختلاف بسیار کمی با یکدیگر دارند.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۱۰ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

آرمان ری بد (+)

«آرمان ری‌بد» دکتری آمار در شاخه آمار ریاضی دارد. از علاقمندی‌های او، یادگیری ماشین، خوشه‌بندی و داده‌کاوی است و در حال حاضر نوشتارهای مربوط به آمار و یادگیری ماشین را در مجله فرادرس تهیه می‌کند.