متغیر تصادفی و توزیع وایبل (Weibull Distribution) — به زبان ساده

متغیر تصادفی «وایبل» (Weibull) یک متغیر تصادفی با مقادیر پیوسته است. تکیه‌گاه این متغیر تصادفی، اعداد حقیقی نامنفی است در نتیجه در مواردی که متغیر تصادفی مربوط به طول عمر باشد، می‌توان از این توزیع استفاده کرد. هر چند این توزیع اولین بار توسط «فرچه» (Frechet) دانشمند فرانوسی در سال ۱۹۲۷ معرفی شد ولی نام این توزیع برگرفته از نام دانشمند و ریاضی‌دان سوئدی «والدی وایبل» (Waloddi Weibull) است که در سال ۱۹۵۱ به بررسی کامل این توزیع پرداخت. همچنین «روزین و راملر» (Rosin & Rammler) در سال ۱۹۳۳ با استفاده از این توزیع، اندازه ذرات مواد در سنگ‌های معدن را مورد بررسی قرار دادند. گاهی توزیع وایبل را به صورت «توزیع وایبول» نیز می‌نویسند.

از آنجایی که در این نوشتار از متغیر تصادفی و تابع احتمال صحبت به میان خواهد آمد بهتر است ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و قابلیت اعتماد (Reliability) برای سامانه‌های منسجم — به زبان ساده را مطالعه کرده باشید. از طرفی خواندن نوشتارهای متغیر تصادفی و توزیع نمایی — به زبان ساده و نوشتار امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها نیز خالی از لطف نیست.

متغیر تصادفی و توزیع وایبل

متغیر تصادفی وایبل و توزیع آن کاربردهای زیادی بخصوص در «تحلیل بقا» (Survival Analysis) و همچنین «قابلیت اعتماد» (Reliability) دارد. بنابراین در حوزه‌های برق و سیستم‌های کنترل و همچنین پیش‌بینی آب و هوا به کار گرفته می‌شود. در این نوشتار به بررسی این متغیر تصادفی خواهیم پرداخت و خصوصیات آن را مرور خواهیم کرد.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

اگر متغیر تصادفی $$X$$ دارای تکیه‌گاه با مقدارهای نامنفی و پیوسته باشد، بطوری که تابع چگالی آن به شکل زیر نوشته شود، آنگاه می‌گوییم این متغیر تصادفی دارای توزیع وایبل با پارامترها $$k$$ و $$\lambda$$ است.

$$\large f(x;\lambda,k) =\begin{cases}\frac{k}{\lambda}\left(\frac{x}{\lambda}\right)^{k-1}e^{-(x/\lambda)^{k}} & x\geq 0 ,\\  \large 0 & x<0,\end{cases}$$

در رابطه بالا، $$\lambda$$ «پارامتر مقیاس» (Scale Parameter) و $$k$$ نیز «پارامتر شکل» (Shape Parameter) است. در این حالت می‌نویسیم $$X\sim W(\lambda, k)$$ و می‌خوانیم «متغیر تصادفی $$X$$ دارای توزیع وایبل با پارامترهای لاندا و کا است.» هر دو این پارامترها نیز مقدارهای مثبت دارند. نمودار تابع چگالی این متغیر تصادفی در تصویر زیر قابل مشاهده است.

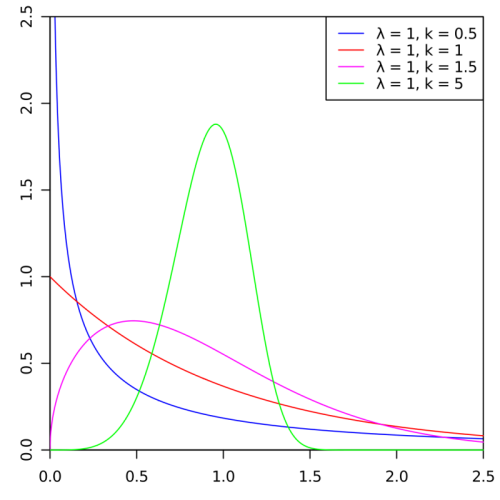
در این نمودار به خوبی مثبت بودن مقادیر متغیر تصادفی دیده می‌شود. همچنین شکل این توزیع با افزایش پارامتر $$k$$ به سمت توزیع نرمال میل می‌کند. همانطور که در تصویر دیده می‌شود، با تغییر مقدار پارامتر $$k$$، شکل تابع چگالی احتمال برای این متغیر تصادفی تغییر می‌کند.

• زمانی که $$0$$ باشد، تابع چگالی با نزدیک شدن مقدار $$x$$ به صفر به سمت بی‌نهایت میل می‌کند. از آنجایی که در این حالت توان $$x$$ یعنی $$k-1$$، در تابع چگالی منفی است ($$k<1$$)، نمودار آن به صورت نزولی است. در چنین حالتی، شیب منحنی در نزدیکی $$x=0$$، منفی بی‌نهایت است.
• اگر $$k=1$$ باشد قسمت مربوط به $$\dfrac{x}{\lambda}$$ از چگالی حذف شده و متغیر تصادفی دارای توزیع نمایی با نرخ شکست $$\lambda$$ خواهد شد. در این حالت تابع چگالی با نزدیک شدن $$x$$ به صفر، به سمت $$\dfrac{1}{\lambda}$$ میل می‌کند. در تصویر با توجه به مقدار $$\lambda=1$$ تابع چگالی احتمال در نقطه $$x=0$$ به مقدار ۱ رسیده است.
• به ازاء مقدار $$k>1$$، با نزدیک شدن مقدار $$x$$ به سمت صفر تابع چگالی نیز به صفر میل می‌کند. به این ترتیب با افزایش مقدار $$x$$ تا رسیدن به مقدار نما (Mode) توزیع، تابع چگالی صعودی و پس از آن نزولی خواهد شد. زمانی که $$1$$ باشد شیب منحنی در زمانی که $$x$$ به سمت صفر میل می‌‌کند به سمت مثبت بی‌نهایت می‌رود. از طرفی زمانی که $$k>2$$ باشد، شیب منحنی تابع چگالی در $$x=0$$ برابر با صفر است.

اگر متغیر تصادفی $$X$$ بیانگر «زمان شکست» (Failure Time) باشد، توزیع وایبل می‌تواند برای توصیف این متغیر تصادفی به کار رود، بطوری که نرخ شکست، متناسب با زمان و به صورت نمایی است. در این حالت پارامتر $$k$$ می‌تواند نشانگر «متوسط نرخ شکست» (Mean Failure Rate) باشد.

• اگر $$k<1$$ باشد، بیانگر نزولی بودن نرخ شکست است. به این معنی که با گذشت زمان، احتمال شکست برای پدیده‌ای با این خصوصیت کاهش می‌یابد.
• اگر $$k=1$$ باشد، نرخ شکست به صورت ثابت خواهد بود.
• برای $$k>1$$ نیز می‌توان صعودی بودن نرخ شکست را در نظر گرفت. به این ترتیب با طول عمر بیشتر، احتمال شکست یا خطا افزایش می‌یابد.

تابع توزیع تجمعی (CDF) برای متغیر تصادفی وایبل به صورت زیر نوشته می‌شود.

$$\large F_X(x)=P(X\leq x)=\begin{cases}1- e^{-(x/\lambda)^k} & x\geq0\\ \large 0 & x<0\end{cases}$$

همچنین نمودار مربوط به تابع توزیع تجمعی این متغیر تصادفی در تصویر زیر دیده می‌شود.

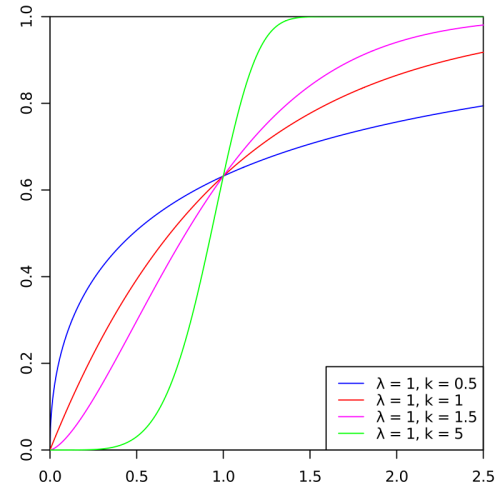
تابع توزیع تجمعی متغیر تصادفی وایبل، زمانی که $$x=\lambda$$ باشد، برابر با $$1-e^{-1}\approx 0.632$$ به ازاء همه مقدارهای $$k$$ خواهد بود. از طرف دیگر اگر مقدار تابع توزیع تجمعی متغیر تصادفی وایبل برابر با $$0.632$$ باشد می‌توان نتیجه گرفت که تقریبا $$x=\lambda$$ است.

توزیع وایبل سه پارامتری

اگر در توزیع وایبل، «پارامتر مکان» (Location Parameter) را با نام $$\theta$$ وارد کنیم، توزیع وایبل سه پارامتری خواهیم داشت. در این حالت تابع چگالی متغیر تصادفی وایبل سه پارامتری و به شکل زیر خواهد بود.

$$\large f(x;k,\lambda, \theta)={k \over \lambda} \left({x - \theta \over \lambda}\right)^{k-1} e^{-({x-\theta \over \lambda})^k}$$

توجه داشته باشید که در این توزیع باید $$x\geq \theta$$ باشد. به این ترتیب $$\theta$$‌ «پارامتر مکان» (Location) و $$k$$ «پارامتر شکل» (Shape Parameter) و در انتها نیز $$\lambda$$، «پارامتر مقیاس» (Scale Parameter) خواهد بود. واضح است که پارامترهای شکل و مقیاس باید مثبت باشند.

نکته: چنانچه مقدار پارامتر مکان ($$\theta$$) برابر با صفر باشد، توزیع به حالت دو پارامتری درخواهد آمد.

خصوصیات متغیر تصادفی وایبل

با توجه به تعریف امید ریاضی، می‌توان مقدارهای «مورد انتظار» (Expected Value) و «واریانس» (Variance) را برای متغیر تصادفی $$X$$ با توزیع وایبل، محاسبه کرد.

$$\large \operatorname{E}(X)=\lambda \Gamma(1+\dfrac{1}{k})$$

$$\large \operatorname{Var}(X)=\lambda^2\left[\Gamma\left(1+\frac{2}{k}\right) - \left(\Gamma\left(1+\frac{1}{k}\right)\right)^2\right]$$

البته می‌توان شیوه نوشتن واریانس را به شکل ساده‌تری نیز انجام داد. در این حالت واریانس برحسب مربع امید ریاضی نوشته خواهد شد.

$$\large \operatorname{Var}(X)=\lambda^2\Gamma(1+\dfrac{2}{k})-\operatorname{E}^2(X)$$

نکته: در روابط بالا که مربوط به امید ریاضی و واریانس متغیر تصادفی وایبل است منظور از $$\Gamma$$ تابع گاما است.

همچنین می‌توان بین توزیع وایبل و توزیع یکنواخت ارتباطی پیدا کرد. فرض کنید $$U\sim U(0,1)$$ آنگاه $$W$$ با تعریف زیر دارای توزیع وایبل با پارامترهای $$k$$ و $$\lambda$$ است.

$$\large W=\lambda(-\ln(U))^{\tfrac{1}{k}}$$

توزیع وایبل نمایی شده (Exponentiated Weibull Distribution)

در سال ۱۹۹۳ «ماهولکار» (Mudholkar) و «سیرواستاوا»  (Srivastava) به بررسی توزیعی گسترش یافته از توزیع وایبل پرداختند که آن را «توزیع وایبل نمایی شده» (Exponentiated Weibull Distribution) نامیدند.

فیلم آموزش فرآیند آماری در کنترل کیفیت آماری (رایگان) در فرادرس

کلیک کنید

در این توزیع «پارامتر شکل» (Shape Parameter) دیگری نیز اضافه شده است. تابع چگالی این توزیع به صورت زیر است.

$$\large f(x;k,\lambda; \alpha) = \alpha \frac{k}{\lambda}[\frac{x}{\lambda}]^{k-1} [1- e^{-(x/\lambda)^k} ]^{\alpha-1} e^{-(x/\lambda)^k}$$

مشخص است که در این توزیع $$k$$ را پارامتر شکل اول و $$\alpha$$ را پارامتر شکل دوم می‌نامند. اگر مقدار $$\alpha$$ برابر با ۱ باشد، توزیع به صورت وایبل دو پارامتری درخواهد آمد. همچنین تابع توزیع تجمعی برای چنین متغیر تصادفی به صورت زیر نوشته می‌شود.

$$\large F(x;k,\lambda; \alpha) = \left[ 1- e^{-(x/\lambda)^k} \right]^\alpha$$

می‌توان نشان داد که متغیر تصادفی با «توزیع وایبل نمایی شده» دارای تابع نرخ خطر صعودی-نزولی و به شکل Bathtub (وانی شکل) است. بنابراین می‌تواند برای بسیاری از پدیده‌های رشد در جوامع انسانی به کار گرفته شود.

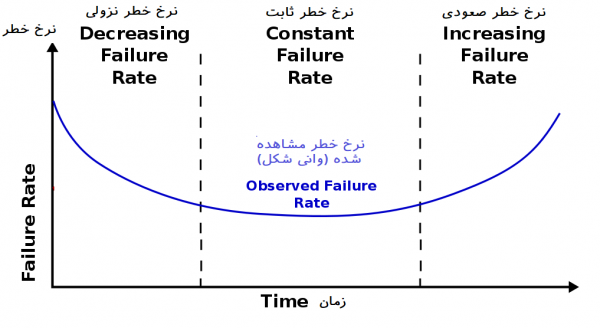
برای مثال دوره زندگی یک انسان دارای نرخ خطر صعودی-نزولی و به شکل وان (Bathtub) است. در ابتدای دوره نوزادی، امکان فوت در اثر بیماری‌ها و خطرات محتمل زیاد است و بنابراین نوزاد احتیاج به مراقبت بیشتری دارد. در دوره کودکی این نرخ کاهش یافته و تا دوره میانسالی تقریبا ثابت است. با گذر از دوره میانسالی و در حدود ۵۰ سالگی این نرخ مجدد افزایش خواهد یافت.

کاربردهای توزیع وایبل

در ادامه به ذکر مثال‌هایی خواهیم پرداخت که با توزیع وایبل در ارتباط است. هرچند نرم‌افزارهای آماری متعددی برای انجام محاسبات مربوط به توزیع‌های آماری وجود دارد، ولی در اینجا به علت سهولت و سادگی نرم‌افزار اکسل، برای انجام محاسبات مربوط به این مثال‌ها از آن کمک خواهیم گرفت.

فیلم آموزش متغیرهای تصادفی (الف) در آمار و احتمال مهندسی (مرور – تست کنکور ارشد) (رایگان) در فرادرس

کلیک کنید

مثال ۱

توزیع طول عمر یک صفحه نمایش حساس رایانه‌ای از توزیع وایبل با پارامترهای $$\lambda=1000$$ ساعت و $$k=0.6$$ پیروی می‌کند. احتمال آنکه صفحه نمایش بیش از ۵۰۰۰ ساعت عمر کند، چقدر است؟ میانگین طور عمر آن را نیز محاسبه کنید.

مشخص است که در این مثال به دنبال محاسبه رابطه زیر هستیم.

$$\large P(X> 5000)$$

ولی به کمک ویژگی‌های که تابع توزیع احتمال دارد، می‌توانیم براساس فرمول زیر احتمال بالا را بدست آوریم.

$$\large P(X> 5000)=1-P(X \leq 5000)$$

برای پاسخ به این سوال از توابع آماری اکسل استفاده می‌کنیم. برای محاسبه احتمال (تابع توزیع تجمعی) وایبل باید از تابع WEIBULL.DIST استفاده کنیم. پارامترهای این دستور به صورت زیر است.

1WEIBULL.DIST(x,alpha,beta,cumulative)

در این تابع $$x$$ مقداری است که باید در آن تابع WEIBULL.DIST محاسبه شود. طبیعتا این مقدار باید مثبت باشد. از طرفی پارامتر alpha نیز همان پارامتر مقیاس ($$\lambda$$‌) در تعریف توزیع متغیر تصادفی وایبل است. همینطور beta نیز بیانگر پارامتر شکل ($$k$$) است. پارامتر آخر (cummulative) نیز یک مقدار منطقی است. اگر این پارامتر، TRUE باشد، تابع WEIBULL.DIST، مقدار تابع توزیع تجمعی احتمال را در نقطه $$x$$‌ محاسبه می‌کند. همچنین با تعیین مقدار FALSE برای این پارامتر، تابع چگالی احتمال وایبل در نقطه $$x$$ بدست خواهد آمد.

WEIBULL(x, β, α, FALSE) = Probability Density Function of  Weibull Distribtion f(x) at x

WEIBULL(x, β, α, TRUE) = Weibull cumulative distribution function F(x) at x

بنابراین برای پاسخ به سوال مطرح شده از فرمول زیر کمک می‌گیریم.

1= WEIBULL.DIST(5000, .6, 1000, TRUE) = 0.92767.

همانطور که دیده می‌شود احتمال اینکه این صفحه نمایش کمتر از ۵۰۰۰ ساعت عمر کند بسیار زیاد است زیرا متوسط زمان خرابی در آن ۱۰۰۰ ساعت در نظر گرفته شده است. در نتیجه مکمل این پیشامد یعنی طول عمری بیش از ۵۰۰۰ ساعت برابر است با $$1-0.92767=0.72$$ که به نظر بسیار کوچک می‌آید. این احتمال نشان می‌دهد که فقط حدود ۷٪ از این نمایشگرها طول عمری بیشتر از ۵۰۰۰ ساعت دارند.

$$\large P(X> 5000)=1-P(X \leq 5000)=۱-0.92767=0.72$$

همینطور، محاسبه میانگین (امید ریاضی) برای این توزیع به صورت زیر است.

$$\large \operatorname{E}(X)=\lambda \Gamma(1+1/k)$$

این رابطه را مطابق با فرمول زیر در اکسل محاسبه می‌کنیم. امید ریاضی چنین متغیری را گاهی با MTTF یا «میانگین زمان خرابی» (Mean Time To Failure) نیز نشان می‌دهند.

1=1000*GAMMA(1 + 1/.6)) = 1,504.575

نکته: در اینجا منظور از GAMMA همان تابع گاما است.

مثال ۲

اگر میانگین زمان خرابی برای یک مولفه با توزیع وایبل برابر با ۱۰۰۰ ساعت و انحراف استاندارد ۴۰۰ ساعت باشد، احتمال اینکه این مولفه بیش از ۲۰۰۰ ساعت کار کند چقدر است؟

ابتدا لازم است که برای توزیع وایبل با این مشخصات، پارامتر $$k$$ و $$\lambda$$ را بدست آورده و مطابق با تابع توزیع تجمعی، چنین احتمالی را محاسبه کنیم. این کار را به کمک دو رابطه زیر انجام می‌دهیم.

$$\large \operatorname{E}(X)=1000= \lambda \Gamma(1+1/k)\\ \large \ln(1000)=\ln(\lambda)+\ln(\Gamma(1+\dfrac{1}{k})$$

رابطه ۱

از طرفی مطابق با شیوه محاسبه واریانس داریم:

$$\large \operatorname{Var}(X)=\lambda^2\left[\Gamma\left(1+\frac{2}{k}\right) - \left(\Gamma\left(1+\frac{1}{k}\right)\right)^2\right]=\lambda^2\Gamma(1+\dfrac{2}{k})-\operatorname{E}^2(X)\\= \large (4000)^2$$

رابطه ۲

در نتیجه رابطه زیر برقرار است:

$$\large \operatorname{Var}(X)+\operatorname{E}^2(X)=160000+1000000=11600000$$

پس مطابق با رابطه ۱ و ۲ می‌توانیم به معادله‌های زیر را بنویسیم.

$$\large \ln(1000)= \ln(\lambda)+\ln(\Gamma(1+\dfrac{1}{k}))$$

رابطه ۳

و همچنین

$$\large \ln(1160000)= ۲\ln(\lambda)+\ln(\Gamma(1+\dfrac{۲}{k}))$$

رابطه ۴

در نتیجه اگر دو برابر رابطه ۳ را از رابطه ۴ کم کنیم می‌توانیم پارامتر $$\lambda$$ را دستگاه حاصل از بین ببریم و معادله را فقط برحسب پارامتر $$k$$‌ حل کنیم.

$$\large \ln(160000)-2\ln(1000)=\ln(\Gamma(1+\dfrac{2}{k})-2 \ln(\Gamma(1+\dfrac{1}{k})$$

که درست مطابق با حال معادله زیر است.

$$\large \ln(\Gamma(1+\dfrac{2}{k}))-2\ln(\Gamma(1+\dfrac{1}{k}))-\ln(1.16)=0$$

به منظور حل این معادله از ابزار Goal Seek اکسل کمک می‌گیریم. کافی است با توجه به تصویر زیر اطلاعات را در کاربرگ ثبت و پنجره Goal Seek را مطابق تصویر تنظیم کنیم. برای دسترسی به این ابزار کافی است از برگه Data، قسمت What-if-Analysis را انتخاب و گزینه Goal Seek را اجرا کنید. پنجره‌ای مطابق تصویر زیر باز خواهد شد.

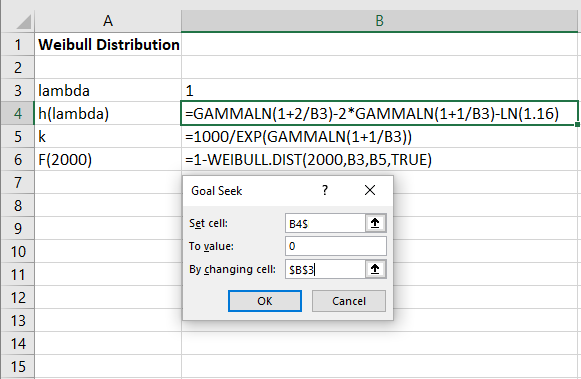
در کادر Set cell باید آدرس سلولی که دارای فرمول بوده و باید مقدار آن به پارامتر To value برسد مشخص می‌شود. همچنین پارامتر By changing cell آدرس سلولی را تعیین می‌کند که باید تغییر کرده تا پارامتر Set cell به مقدار To value برسد. واضح است که در اینجا پارامتر Set cell یک سلول وابسته است که آدرس سلول پیش‌نیاز آن در پارامتر by changing cell تعیین شده است.

نکته: برای حل این معادله ابتدا به سلول B3 که هدف، بدست آوردن آن است، مقداری اختیاری (مثلا ۱) نسبت داده تا ابزار Goal Seek بتواند معادله را حل کند.

پس از فشردن دکمه OK، اکسل با مقدار دهی به سلول B3، سعی می‌کند مقدار سلول B4 را به صفر نزدیک کند. نتیجه این تلاش در تصویر زیر دیده می‌شود.

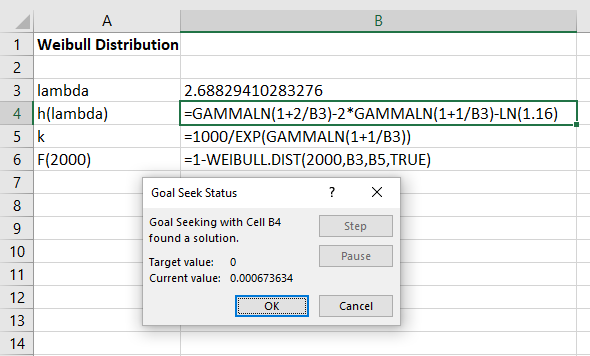
به این ترتیب مقدار پارامتر lambda تقریبا برابر با 2.6883 می‌باشد. به همین ترتیب براساس محاسبات صورت گرفته در کاربرگ مقدار پارامتر k نیز طبق فرمول نوشته شده در سلول B4 محاسبه می‌شود که برابر با 1124.667 است.

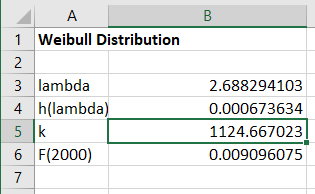
به این ترتیب به کمک تابع زیر می‌توانیم مقدار احتمال را براساس این پارامترها بدست آوریم.

$$\large P(X>2000)=1-P(X\leq 2000)=1-0.99=0.001$$

1=1-WEIBULL.DIST(2000,B3,B5,TRUE)

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس