قابلیت اعتماد سامانه منسجم — به زبان ساده

با توجه به پیشرفتهای فنآوری در زمینههای مختلف، برای انجام کارها و حتی امور روزانه به دستگاهها و تجهیزات زیادی وابسته هستیم. معمولا این دستگاهها از سامانههای سختافزاری یا نرمافزاری مختلفی بهره میبرند که دارای اجزای کوچکتری هستند. طول عمر دستگاهها و اطمینان از عملکرد این گونه سامانهها وابسته به طول عمر و عملکرد صحیح اجزایشان دارد که با توجه به قوانین مربوط به تئوری احتمال محاسبه میشود. در این مطلب به مبحث «قابلیت اعتماد» (Reliability) برای «سامانههای منسجم» (Coherent Systems) میپردازیم.
به عنوان پیشزمینه، بهتر است مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و آزمایش تصادفی، پیشامد و تابع احتمال را ابتدا بخوانید تا با مفاهیم اولیه مربوط به تئوری احتمال آشنا شوید. ذکر این نکته نیز اهمیت دارد که گاهی به قابلیت اعتماد، قابلیت اطمینان نیز گفته میشود.
قابلیت اعتماد سامانه منسجم
عملکرد صحیح دستگاه به پارامترهای متعددی نظیر عوامل تصادفی و غیرتصادفی مرتبط است. از آنجایی که ممکن است تاثیر بعضی از این گونه عوامل بر عملکرد دستگاه، دارای الگوی احتمالی باشد، تئوریهای احتمال در مبحث قابلیت اعتماد و به منظور تعیین عملکرد یا طول عمر سامانه، اهمیت زیادی پیدا میکنند.
به این ترتیب مبحث قابلیت اعتماد مرتبط با فعالیت صحیح و طول عمر سامانهها یا سیستمها محسوب میشود و بهتر است ابتدا با چند مفهوم اولیه که در این مبحث زیاد به کار گرفته میشوند آشنا شویم.
- تعریف سامانه: یک «سامانه» (System) ترکیبی از اجزاء مستقل یا وابسته است که هدف مشخصی را دنبال میکند. اجزای یک سامانه ممکن است خود دارای فعالیتی هدفدار باشند که در این صورت آنها را هم، سامانه مینامیم.
- طول عمر: منظور از «طول عمر» (Life Time) دستگاه، بازه زمانی است که در آن دستگاه یا سامانه دارای عملکرد صحیحی است. در خارج از بازه طول عمر، دستگاه دچار خطا میشود.
- سامانه منسجم: اگر عملکرد و در نتیجه طول عمر یک سامانه به عملکرد و طول عمر اجزاء یا مولفههای آن وابسته باشد، آن را یک سامانه منسجم مینامیم. در نتیجه طول عمر سامانه منسجم، مستقل از طول عمر «مولفههای نامربوط» (Irrelevant Components) محسوب میشود. منظور از مولفههای نامربوط، اجزایی از سیستم است که در عملکرد آن موثر نیستند.

تابع عملکرد سامانه و اجزای آن
فرض کنید یک سامانه از n جزء یا مولفه تشکیل شده است. یعنی X، یک سامانه با برداری از n مولفه است که آن را به صورت $$X=\{x_1,x_2,\ldots,x_n\}$$ نشان میدهیم. از آنجایی که الگوی احتمالی برای عملکرد سامانه و اجزای آن وجود دارد، طبیعی است که از متغیر تصادفی برنولی به منظور نشان دادن سالم بودن هر مولفه یا سامانه استفاده کنیم. در نتیجه اگر $$X_i$$ را متغیر تصادفی مربوط به عملکرد جزء iام در نظر بگیریم، میتوانیم وضعیت فعالیت آن را به صورت زیر نشان دهیم.
$$x_i=\begin{cases}0 &Malfunction \\1 & Function\end{cases}$$
این رابطه نشان میدهد که جزء یا مولفه iام سامانه چه عملکردی دارد. با توجه به توزیع برنولی میدانیم که تابع احتمال برای این جزء به صورت زیر است.
$$P(x_i=y)=\displaystyle \begin{cases}(1-p_i) &y=0 \\p_i & y=1 \end{cases}$$
در این حالت میتوانیم بگویم متغیر تصادفی مربوط به عملکرد هر مولفه یا جزء مثل $$x_i$$ دارای توزیع برنولی با احتمال $$p_i$$ است. به این ترتیب برای یک سامانه n مولفهای میتوان بردار احتمال عملکرد را با $$p=\{p_1,p_2,\ldots,p_n\}$$ نشان داد.
بر همین مبنا قابلیت اعتماد یا احتمال عملکرد بدون خطای مولفه را میتوان براساس امید ریاضی (متوسط حالتهایی که مولفه فعال است) در نظر گرفت. در نتیجه قابلیت اعتماد برای مولفه iام به صورت زیر قابل محاسبه است.
$$E(X_i)=P(X_i=1)=p_i$$
حال اگر عملکرد سامانه را که با $$\Phi(X)$$ نشان میدهیم، به عنوان تابعی از عملکرد اجزاء آن بدانیم، خواهیم داشت:
$$\Phi(X)=\begin{cases}0 &System\;Malfunction \\1 & System\; Functions\end{cases}$$
با توجه به محاسبه قابلیت اعتماد برای هر مولفه، میتوان احتمال اینکه سامانه بدون خطا فعالیت کند را با $$P(\Phi(X)=1)$$ در نظر گرفت. باز هم با در نظر گرفتن دو مقداری بودن برای تابع عملکرد سامانه، میتوان امید ریاضی تابع عملکرد را به عنوان قابلیت اعتماد سامانه در نظر گرفت. قابلیت اعتماد برای سامانه را با $$h(p)$$ نشان میدهند. بنابراین طبق این فرض میتوان نوشت:
$$h(p)=E(\Phi(X))=P(\Phi(X)=1)$$
تابع $$\Phi$$ و نحوه محاسبه تابع احتمال آن با توجه به ساختار و ارتباط بین اجزاء و مولفهها تعیین میشود. در ادامه به معرفی چند نوع سامانه و نحوه ارتباط بین مولفهها در آنها میپردازیم.
سامانه متوالی
«سامانه متوالی» (Series) یکی از سادهترین روشهایی است که نحوه ارتباط بین اجزا را مشخص میکند. در این گونه سامانهها، عملکرد همه اجزاء، فعالیت صحیح سامانه را به همراه دارد. در حقیقت در این نوع سامانه، کافی است فقط یک جزء غیرفعال شود تا سامانه از کار بیافتد. این نوع سامانهها را گاهی سامانههای سری نیز مینامند.
برای مثال، مدارهای سری در الکتریسته و الکترونیک از این نوع سامانهها محسوب میشوند.
در این حالت تابع عملکرد سامانه سری را میتوان به صورت زیر نوشت:
$$\Phi(X)=\prod_{i=1}^n(x_i)$$
از آنجایی که همه مقدارها برای $$x_i$$ با ۰ یا ۱ مشخص میشود، میتوان تابع عملکرد سامانه متوالی را به صورت زیر نیز در نظر گرفت:
$$\Phi(X)=\min(x_1,x_2,\ldots ,x_n)$$
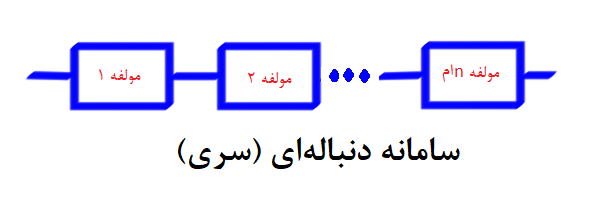
حال محاسبه قابلیت اعتماد برای چنین سامانهای با در نظر گرفتن شرط استقلال مولفهها به صورت زیر خواهد بود.
$$h(p)= E(\Phi(X))=E(\prod_{i=1}^n x_i)=\prod_{i=1}^n(E(x_i))=\prod_{i=1}^n p_i$$
با توجه به این رابطه، مشخص میشود که هر چه تعداد اجزای سامانه متوالی بیشتر شود، قابلیت اعتماد کاهش مییابد. همچنین مشخص است که با افزایش قابلیت اعتماد مولفهها، قابلیت اعتماد سامانه نیز افزایش خواهد یافت.
نکته: اگر احتمال عملکرد یا قابلیت اعتماد هر مولفه در سامانههای متوالی را ثابت و برابر با $$\rho$$ در نظر بگیریم، قابلیت اعتماد سامانه به صورت $$\rho^n$$ در خواهد آمد.
سامانه موازی
«سامانه موازی» (Parallel) یکی از سادهترین روشهایی است که نحوه ارتباط بین اجزا را مشخص میکند. در این گونه سامانهها، عملکرد حداقل یک جزء، فعالیت صحیح سامانه را به همراه دارد. در حقیقت در این نوع سامانه، فعالیت فقط یک جزء کافی است تا سامانه فعال باقی بماند. به بیان دیگر اگر همه اجزاء سامانه غیرفعال باشند، آنگاه فعالیت آن نیز متوقف میشود. برای مثال، مدارهای موازی در الکتریسته و الکترونیک از این نوع سامانهها محسوب میشوند.
در این حالت تابع عملکرد سامانه موازی را میتوان به صورت زیر نوشت:
$$\Phi(X)=\prod_{i=1}^n1-(1- x_i)$$
با توجه به اینکه وضعیت فعالیت هر مولفه برحسب مقدارهای 0 و ۱ تعیین میشود، میتوان از رابطه زیر نیز برای معرفی تابع عملکرد سامانه موازی استفاده کرد.
$$\Phi(X)=\max(x_1,x_2,\ldots ,x_n)$$
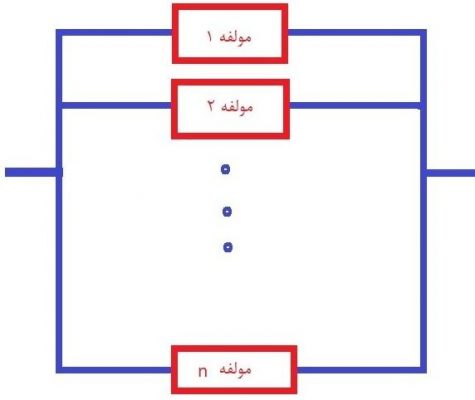
در چنین سامانهای با فرض استقلال مولفهها، تابع قابلیت اعتماد سامانه به صورت زیر در خواهد آمد:
$$h(p)= E(\Phi(X))=E(۱-\prod_{i=1}^n (۱-x_i))=1-\prod_{i=1}^n((1-E(x_i))=1-\prod_{i=1}^n (1-p_i)$$
با توجه به این رابطه مشخص میشود که قابلیت اعتماد سامانه تابعی صعودی از تعداد اجزای آن و همچنین قابلیت اعتماد آنها است. به این معنی که با افزایش تعداد مولفههای سامانه موازی، قابلیت اعتمادش افزایش مییابد.
نکته: اگر قابلیت اعتماد هر جزء در سامانههای موازی برابر با $$\rho$$ باشد، قابلیت اعتماد سامانه به صورت $$1-(1-\rho)^n$$ نوشته میشود.
سامانه k از n
در این گونه سامانهها حداقل باید k مولفه فعال باشند تا سامانه در حال کار باقی بماند. تابع عملکرد چنین سامانههایی را میتوان با رابطه زیر نشان داد:
$$\Phi(X)=\begin{cases}0 & \sum_{i=1}^n x_i\geq k \\0 & otherwise\end{cases}$$
در چنین سامانهای با فرض استقلال مولفهها، تابع قابلیت اعتماد سامانه به صورت نوشته میشود:
$$h(p)= E(\Phi(X))=P(\sum_{i=1}^n x_i\geq k)$$
اگر در چنین سامانهای قابلیت اعتماد مولفهها ثابت و برابر باشد ($$p=p_1=p_2=\ldots p_n$$) میتوان توزیع مجموع متغیرهای تصادفی برنولی مستقل را توزیع دو جملهای دانست و رابطه بالا را به صورت سادهتر زیر نمایش داد:
$$h(p)= \sum_{i=k}^n {n \choose i} p^i(1-p)^{n-i}$$
با توجه به این رابطه مشخص میشود که قابلیت اعتماد سامانه با فرض ثابت بودن n تابعی نزولی از k است. همچنین اگر k ثابت در نظر گرفته شود، یک تابع صعودی از n خواهد بود. به این معنی که اگر تعداد مولفهها ثابت باشند، احتمال عملکرد صحیح سامانه با افزایش تعداد مولفههای فعال، کاهش مییابد. برعکس، اگر تعداد حداقل مولفههای سالم سامانه ثابت باشد، با افزایش تعداد مولفهها، قابلیت اعتماد سامانه نیز افزایش خواهد یافت.
مثال ۱
فرض کنید میخواهیم قابلیت اعتماد را برای یک سامانه الکترونیکی که مدار آن از اتصال 5 مولفه متوالی تشکیل شده است، محاسبه کنیم. اگر احتمال عملکرد صحیح هر جزء برابر با 0.5 باشد، قابلیت اعتماد چنین سامانهای برابر است با:
$$h(p)=p^5=(0.5)^5=\dfrac{1}{32}$$
در این حالت، مشخص است که قابلیت اعتماد چنین سیستمی خیلی کوچکتر از مولفههای آن است. قبلا هم دیده شد که قابلیت اعتماد برای سیستمهای متوالی با تعداد مولفهها رابطه عکس دارد.
مثال ۲
فرض کنید در دستگاهی مشابه مثال ۱، نحوه اتصال مولفهها به صورت موازی باشد. در نتیجه مقدار قابلیت اعتماد چنین سامانهای برابر است با:
$$h(p)=1-(1-p)^5=1-(1-0.5)^5=1-\dfrac{1}{32}=\dfrac{31}{32}$$
در این سیستم، قابلیت اعتماد تقریبا با ۱ برابر است. قبلا هم دیدیم که در سیستم موازی با افزایش مولفهها، قابلیت اعتماد سامانه افزایش مییافت.
مثال ۳
در یک سامانه k از n، تعداد اجزا برابر با ۱۰ و تعداد حداقل مولفههای فعال برای عملکرد صحیح سامانه برابر با ۵ است. اگر قابلیت اعتماد برای هر یک از اجزا ثابت و برابر با 0.5 باشد، قابلیت اعتماد سامانه به صورت زیر محاسبه میشود.
$$P(\sum_{i=1}^{10} x_i\geq 5)=$$
$$\sum_{i=5}^10 {10 \choose i}(0.5)i(0.5)^{10-i}=$$
$${10 \choose 5}(0.5)^5(0.5)^{1051}+{10 \choose 6}(0.5)^6(0.5)^{10-6}+$$
$${10 \choose 7}(0.5)^7(0.5)^{10-7}+{10 \choose 8}(0.5)^8(0.5)^{10-8}+$$
$${10 \choose 9}(0.5)^9(0.5)^{10-9}+{10 \choose 10}(0.5)^10(0.5)^{10-10}=0.623$$
البته برای راحتی کار میتوان از تابع توزیع دو جملهای استفاده کرد و احتمال زیر را به کمک جداول مربوط به توزیع تجمعی متغیر تصادفی دو جملهای به دست آورد:
$$P(\sum_{i=1}^{10} x_i\geq 5)=1-P(\sum_{i=1}^{10} x_i\leq 4)=1-0.377=0.623$$
در چنین سیستمی به نظر میرسد که قابلیت اعتماد سیستم از اجزای آن بیشتر است. همین امر میتواند توجیهی برای استفاده از چنین سامانههایی باشد.
اگر مطلب بالا برای شما مفید بوده است، آموزشهایی که در ادامه آمدهاند نیز به شما پیشنهاد میشود.
- مجموعه آموزشهای دروس مهندسی صنایع
- مجموعه آموزشهای مهندسی کنترل
- آموزش مقدماتی نظریه قابلیت اعتماد
- آموزش قابلیت اطمینان در سیستم های قدرت
- مجموعه آموزشهای نرمافزارهای آماری
- مدل سازی، برازش و تخمین
- آموزش حل مسائل قابلیت اطمینان در شبکه به صورت چند هدفه در متلب
- داده های سانسور شده (Censored Data) در آمار — به زبان ساده
^^










