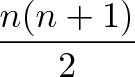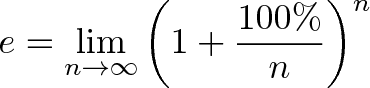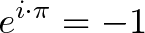علامت مساوی (=) در ریاضیات – به زبان ساده

در اغلب موارد این نکته را فراموش می‌کنیم که ریاضیات زبانی برای انتقال ایده‌ها است. از آنجا که جمله «دو به علاوه سه برابر با پنج است.» طولانی است به جای آن با جایگزینی اعداد و عملگرها به صورت نمادین می‌نویسیم: «3 + 2 مساوی 5 است». اما از این هم بهتر می‌توان عمل کرد. رابرت رکورد (Robert Recorde) در سال 1557 علامت مساوی را ابداع کرد که به صورت دو خط موازی روی هم (=) نمایش می‌یابد. توجیه وی چنین بود که دو خط موازی بهترین نمایش از برابری هستند.

بدین ترتیب خوانایی «5 = 3 + 2» بسیار آسان‌تر است. متأسفانه معنای مساوی، بسته به زمینه موضوعی متفاوت است. برای مثال اگر دوست برنامه‌نویسی داشته باشید، می‌توانید از او بخواهید که تفاوت بین «=»، «==» و «===» را برای شما توضیح دهد.

گزاره الف «مساوی» ب است، یک نتیجه‌گیری کلی است و باید مشخص شود که چه رابطه خاصی بین این دو وجود دارد. در ادامه برخی از این روابط که معنای ضمنی تساوی را ارائه می‌دهند، معرفی کرده‌ایم.

ساده‌سازی

می‌توان تصور کرد که «5 = 3 + 2» همان «3 + 2 را می‌توان به صورت 5 ساده‌سازی کرد» است. علامت مساوی شکل پیچیده سمت چپ را به معادل ساده‌تر سمت راست تبدیل می‌کند.

انتساب موقت

عبارت‌هایی مانند «سرعت = 50» به این معنی هستند که «سرعت در این وضعیت برابر با 50 است». این معنی تنها برای مسائل خاص مورد بررسی مناسب است و نه برای بیان یک واقعیت کلی. بدین ترتیب این نوع از تساوی، تعمیمی کلی محسوب نمی‌شود.

اتصال بنیادی

یک حقیقت ریاضی را در نظر بگیرید، مثلاً a² + b² = c² که a، b و c اضلاع یک مثلث قائم‌الزاویه باشند. در این صورت علامت مساوی به صورت «همواره باید برابر باشد» یا «می‌توان این طور در نظر گرفت» خوانده می‌شود، زیرا یک رابطه را بیان می‌کند و نه یک انطباق. عبارت حسابی 3² + 4² = 5² یک ساده‌سازی است چون از لحاظ هندسی a² + b² = c² یک حقیقت ریاضی عمیق است.

فرمول جمع اعداد 1 تا n به صورت زیر است:

که آن را می‌توان نوعی بازآرایی هندسی، ترکیب، محاسبه میانگین و یا حتی فهرست‌بندی تلقی کرد.

تعریف واقعی

عبارت زیر را در نظر بگیرید:

این عبارت تعریفی مبتنی بر انتخاب ما است. سمت چپ میانبری برای سمت راست محسوب می‌شود. این شکل استفاده از علامت مساوی شبیه انتساب موقت است؛ اما برای «واقعیت‌های» استفاده می‌شود که در سناریوهای مختلف تغییر نمی‌یابند. یعنی در این مورد، این تعریف برای همه مقادیر پابرجا است؛ اما در مورد معنای انتساب موقت، سرعت 50 می‌تواند تغییر کند.

محدودسازی

این تعریف برای علامت مساوی، کمی پیچیده است. ما می‌توانیم بنویسیم:

• x + y = 5
• x – y = 3

که نشان می‌دهد شرایطی که ما می‌خواهیم صحیح هستند. ما عبارت فوق را به این صورت می‌خوانیم که «x + y در صورت امکان، باید 5 باشد» و «x – y در صورت امکان باید 3 باشد». اگر قیود (x=4,y=1) را داشته باشیم، عالی خواهد بود.

اگر عبارت‌های فوق به صورت زیر بودند:

• x + y = 5
• 2x + 2y = 9

در این صورت معادلات می‌توانند به صورت منفرد صحیح باشند؛ اما به صورت مجموع با هم قابل حل نیستند.

مثال: ساده‌سازی فرمول اویلر

بررسی معنی علامت مساوی به ما کمک کند که فرمول اویلر را کدگشایی کنیم:

به نظر شما معنی علامت مساوی در عبارت فوق چیست؟ ممکن است تصور کنید که این علامت به معنی ساده‌سازی است و نتیجه محاسبات سمت چپ را در سمت راست نشان می‌دهد. اما این توضیح کافی نیست و رابطه‌ای بنیادی وجود دارد که باید کشف شود.

در عبارت فوق e^i.π به همان مقصدی اشاره می‌کند که 1- اشاره می‌کند. در واقع مانند دو انگشتی که به سمت ماه گرفته شده باشند.

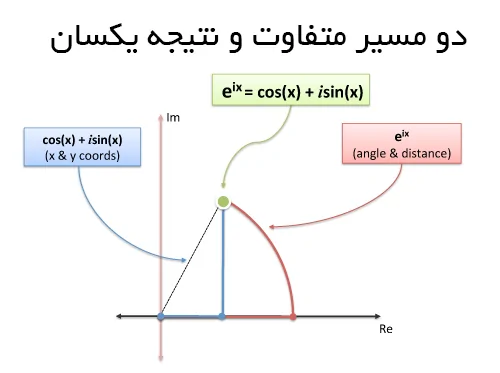
هر دو سمت عبارت فوق روشی برای توضیح این واقعیت هستند که «سمت مقابل دایره، 180 درجه فاصله دارد.» 1- به طور مستقیم این فاصله را از روی قطر طی می‌کند و به سمت مقابل دایره می‌رسد، در حالی که e^i.π مسیر منحنی را انتخاب می‌کند و حول بُعد فرضی می‌چرخد تا به نقطه مقابل برسد. این رابطه برای هر نقطه‌ای روی دایره صدق می‌کند و می‌توان با طی خط مستقیم یا مسیری روی منحنی دایره به نقطه مقابل آن رسید.

«دو مسیر مقصد مشترکی دارند» این معنایی است که از علامت مساوی در رابطه فوق برداشت می‌شود. می‌بینید که علامت مساوی معانی بسیار متفاوتی می‌تواند داشته باشد. شما نیز اگر معنای دیگری برای علامت مساوی می‌شناسید، می‌توانید آن را در بخش نظرات این نوشته با ما و دیگر خوانندگان فرادرس در میان بگذارید.

اگر این نوشته مورد توجه شما قرار گرفته است، پیشنهاد می‌کنیم موارد زیر را نیز ملاحظه کنید:

• آموزش ریاضی پایه دانشگاهی
• نماد انتگرال — با سرگذشت جالب این علامت ریاضی آشنا شوید
• مجموعه آموزش‌های ریاضیات
• آموزش ریاضیات عمومی ۱
• علائم هندسی در ریاضیات — به زبان ساده
• مجموعه آموزش‌های محاسبات عددی

==