توزیع مثلثی و توزیع ذوزنقه‌ ای — به زبان ساده

دو توزیع احتمالی که در منطق فازی برای ایجاد اعداد یا مجموعه‌های فازی به کار گرفته می‌شوند، توزیع‌ مثلثی (Triangle Distribution) و ذوزنقه‌ای (Trapezoidal Distribution) هستند. در این نوشتار به بررسی این دو توزیع می‌پردازیم و خصوصیات هر یک را مورد کاوش قرار می‌دهیم. برای آشنایی بیشتر با موضوع تابع احتمال و تابع توزیع مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کنید. همچنین خواندن متن مجموعه فازی (Fuzzy Set) — به زبان ساده خالی از لطف نیست.

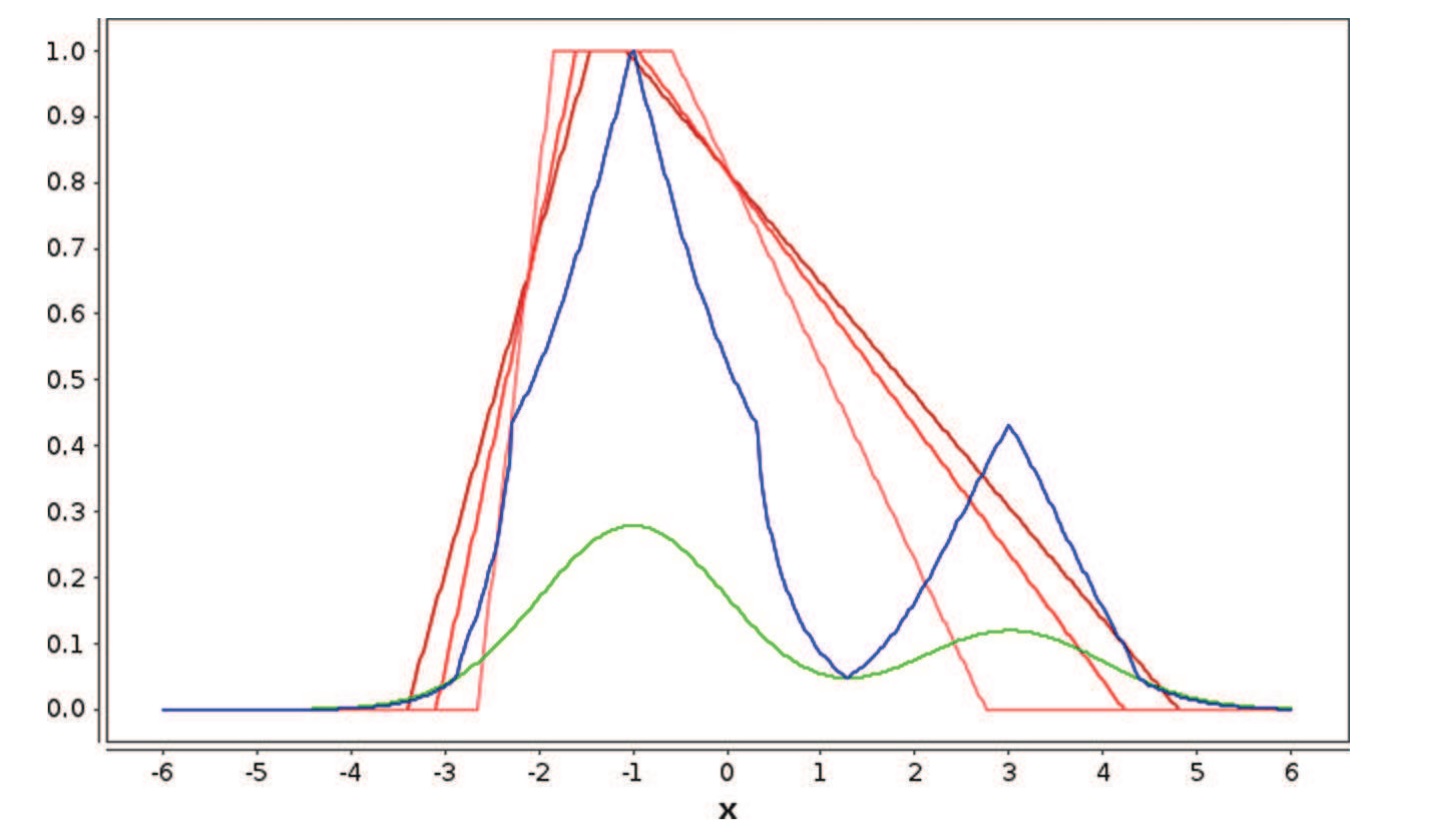
توزیع مثلثی و ذوزنقه‌ای

متغیر تصادفی مثلثی و ذوزنقه‌ای از گروه متغیرهای تصادفی پیوسته محسوب می‌شوند. هر یک از این توزیع‌ها کاربردهای مخصوص خود را دارند. ابتدا به بررسی توزیع مثلثی و متغیر تصادفی آن می‌پردازیم.

فیلم آموزش مدیریت ریسک پروژه با نرم افزار پرت مستر Pertmaster در فرادرس

کلیک کنید

توزیع مثلثی (Triangle Distribution)

متغیر تصادفی مثلثی، دارای دو کران پایین $$a$$ و بالای $$b$$ است. پس تکیه‌گاه آن اعداد حقیقی در فاصله $$a$$ تا $$b$$ خواهد بود. توزیع مثلثی دارای سه پارامتر $$a, b, c$$ است. اولین پارامتر آن یعنی $$a$$ بیانگر کران پایین برای مقدارهای متغیر تصادفی است. پارامتر دوم نیز بیانگر کران بالا برای متغیر تصادفی $$X$$ است. از طرفی پارامتر $$c$$ نیز همان نما یا mode توزیع است.

بین این پارامترها در توزیع مثلثی رابطه‌ زیر برقرار است.

$$\large a \in (-\infty,\infty);\;\;\;a$$

با توجه به قرارگیری $$x$$ در فاصله‌های مختلف، شکل تابع احتمال برای این متغیر تصادفی $$X$$ به صورت زیر نوشته می‌شود.

$$\large f_X(x)=\begin{cases}0&{\text{for }}x<a,\\{\frac {2(x-a)}{(b-a)(c-a)}}&{\text{for }}a\leq x<c,\\[4pt]{\frac {2}{b-a}}&{\text{for }}x=c,\\[4pt]{\frac {2(b-x)}{(b-a)(b-c)}}&{\text{for }}c<x\leq b,\\[4pt]0&{\text{for }}b<x.\end{cases}$$

شکل تابع احتمال برای چنین متغیر تصادفی مانند زیر است.

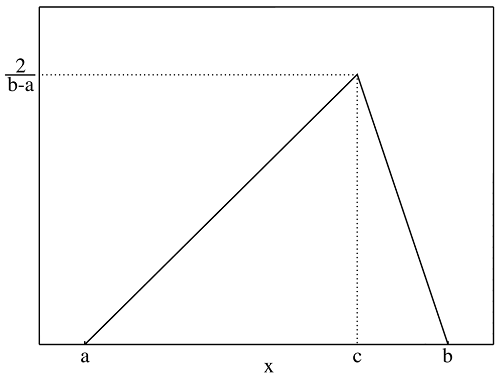
همچنین تابع توزیع احتمال تجمعی و نمودار آن برای متغیر تصادفی مثلثی $$X$$ به صورت زیر در خواهد آمد.

$$\large P(X\leq x)=F_X(x)= \begin{cases} 0 & \text{for } x \leq a, \\[2pt] \frac{(x-a)^2}{(b-a)(c-a)} & \text{for } a < x \leq c, \\[4pt] 1-\frac{(b-x)^2}{(b-a)(b-c)} & \text{for } c < x < b, \\[4pt] 1 & \text{for } b \leq x. \end{cases}$$

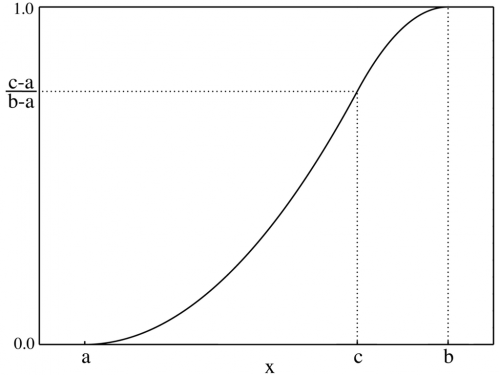
نکته:  اگر داشته باشیم $$c=\frac{a+b}{2}$$ آنگاه توزیع مثلثی را متقارن می‌نامند.

خصوصیات تابع توزیع مثلثی

براساس تابع احتمال و توزیع مثلثی می‌توان امید ریاضی، نما و واریانس متغیر تصادفی ($$X$$) را محاسبه کرد. امید ریاضی این متغیر تصادفی برابر است با:

$$\large E(X)= \frac{a+b+c}{3}$$

همانطور که قبلا اشاره شد نما یا mode این متغیر تصادفی برابر است با $$c$$. همچنین واریانس برای این متغیر تصادفی به صورت زیر محاسبه می‌شود.

$$\large Var(X)=\frac{a^2+b^2+c^2-ab-ac-bc}{18}$$

در حالت خاص اگر $$a=0$$ و $$b=c=۱$$ باشد، تابع احتمال به صورت زیر در خواهد آمد.

$$\large f_X(x)=2x ,\;\;\;0\leq x\leq1$$

به این ترتیب امید ریاضی برای این متغیر تصادفی برابر است با $$\frac{2}{3}$$ و واریانس نیز $$\frac{1}{18}$$ خواهد بود. مشخص است که نما در این حالت همان ۱ محاسبه می‌شود.

توزیع مثلثی را می‌توان براساس دو متغیر تصادفی یکنواخت استاندارد نیز بیان کرد. فرض کنید $$X_۱, \;X_2$$ دو متغیر تصادفی یکنواخت پیوسته استاندارد باشند که از یکدیگر مستقلند. در این حالت اگر $$Y=|X_1-X_2|$$ باشد، آنگاه $$Y$$‌ دارای توزیع مثلثی با پارامترهای $$a=0,\; b=1,\;c=0$$ است. در نتیجه تابع احتمال، تابع توزیع احتمال تجمعی، امید ریاضی و واریانس آن به صورت زیر محاسبه می‌شود.

$$\large \begin{aligned}f(x)&=2-2x\;\;{\text{ for }}\;\;0\leq x<1\\ \large F(x)&=2x-x^{2}\;\;{\text{ for }}0\leq x<1\\ \large E(X)&={\frac {1}{3}}\\ \large Var(X)&={\frac {1}{18}}\end{aligned}$$

مثال

یک فروشگاه زنجیره‌ای غذا، تصمیم دارد یک شعبه جدید در شهر ایجاد کند. پیش‌بینی می‌شود که حداقل فروش در هفته برابر با ۱۰۰۰ دلار و حداکثر فروش نیز ۶۰۰۰ دلار باشد. متوسط فروش نیز حدود ۳۰۰۰ دلار در نظر گرفته می‌شود. با توجه به این توضیحات به نظر می‌رسد که توزیع احتمالی برای میزان فروش این شعبه از توزیع مثلثی با پارامترهای $$a=1000, b=6000$$ و $$c=3000$$ تبعیت می‌کند. شکل این توزیع در تصویر زیر دیده می‌شود.

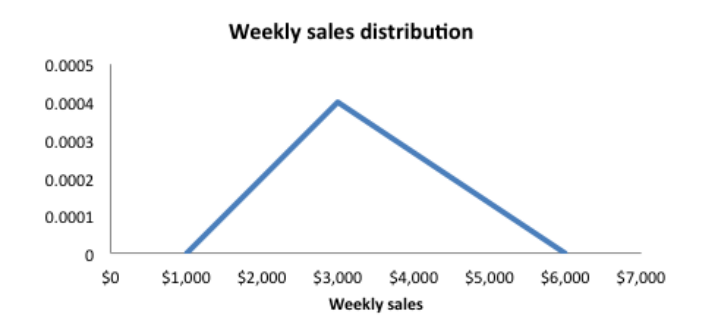
اگر این شعبه، میزان فروشی کمتر از ۲۰۰۰ دلار در هفته داشته باشد، از نظر مدیریت توجیه اقتصادی برای راه‌اندازی آن وجود ندارد. بنابراین لازم است براساس این توزیع احتمالی، محاسبه $$Pr(X<2000)$$ صورت گیرد. با توجه به مفهوم و رابطه‌ای که بین تابع احتمال و تابع احتمال توزیع تجمعی وجود دارد، باید سطح زیر منحنی تابع احتمال تا نقطه x=2000 را محاسبه کنیم.

با استفاده از قانون مساحت مثلث‌ها این محاسبه را انجام می‌دهیم. به یاد دارید که مساحت مثلث به صورت نصف حاصلضرب ارتفاع در قاعده محاسبه می‌شود.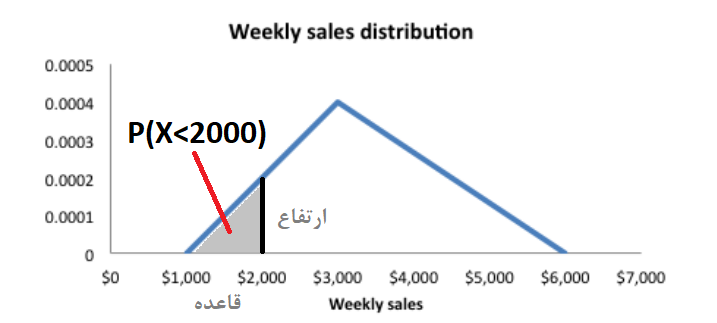

از آنجایی که قاعده برابر با ۱۰۰۰ دلار است، کافی است که ارتفاع را محاسبه کنیم. مقدار ارتفاع نیز همان مقدار تابع احتمال در نقطه ۲۰۰۰ است. پس داریم.

$$\large f_X(2000)=\dfrac{2(2000-a)}{(b-a)(c-a)}=\dfrac{2\times (2000-1000)}{(6000-1000)\times(3000-1000)}=0.0002$$

در نتیجه مساحت سطح زیر منحنی (مساحت مثلث) برابر است با

$$\large P(X<2000)=\frac{1}{2}\times 1000\times 0.0002=0.1$$

پس با احتمال 0.1 میزان فروش چنین شعبه‌ای کمتر از ۲۰۰۰ دلار است. از آنجایی که این میزان ریسک برای شرکت قابل تحمل است، تصمیم گرفته می‌شود که شعبه تاسیس شود.

توزیع ذوزنقه‌ای (Trapezoidal Distribution)

متغیر تصادفی ذوزنقه‌ای، دارای دو کران پایین $$a$$ و بالای $$d$$ به عنوان پارامترهای توزیع است. پس تکیه‌گاه آن اعداد حقیقی در فاصله بسته $$a$$ تا $$d$$ خواهد بود. توزیع ذوزنقه‌ای دارای دو پارامتر دیگر نیز هست.

فیلم آموزش کاربرد اکسل Excel در مهندسی صنایع در فرادرس

کلیک کنید

این دو پارامتر به نام‌های $$b$$ و $$c$$ بیانگر سطوحی هستند که آغاز و پایان ضلع بالایی ذوزنقه را نشان می‌دهند.

بین پارامترهای $$a, b, c, d$$ روابط زیر برقرار است.

$$\large a\;(a \large b\;(a\leq b \large c\;(b \large d\;(c\leq d) - upper\;bound$$

اگر $$X$$‌ متغیر تصادفی با توزیع ذوزنقه‌ای با پارامترهای $$a, b, c, d$$ باشد، تابع احتمال آن به صورت زیر نوشته خواهد شد.

$$\large \begin{cases}{\dfrac {2}{d+c-a-b}}{\dfrac {x-a}{b-a}}&{\text{for }}a\leq x<b\\ \large {\dfrac {2}{d+c-a-b}}&{\text{for }}b\leq x<c\\ \large {\dfrac {2}{d+c-a-b}}{\dfrac {d-x}{d-c}}&{\text{for }}c\leq x\leq d\end{cases}$$

در ادامه تصویر مربوط به نمودار این تابع احتمال دیده می‌شود.

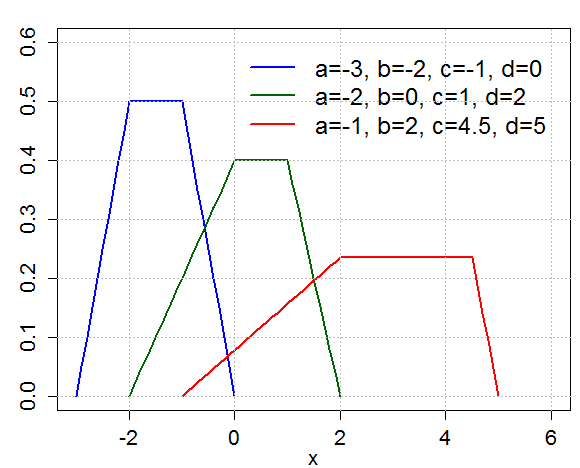
با توجه به رابطه‌ای که بین تابع توزیع احتمال و تابع توزیع احتمال تجمعی وجود دارد مقدار احتمال $$Pr(X$$ براساس رابطه زیر قابل محاسبه است.

$$\large P(X$$

نمودار تابع توزیع احتمال تجمعی برای متغیر تصادفی با توزیع ذوزنقه‌ای نیز در تصویر زیر قابل مشاهده است.

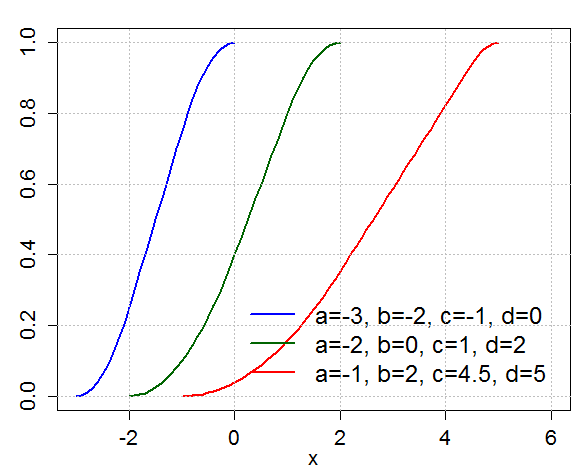
خصوصیات تابع توزیع ذوزنقه‌ای

با توجه به شکل تابع احتمال، مشخص است که تمام نقاطی که در فاصله $$[c,b]$$ قرار دارند، مد یا نمای توزیع محسوب می‌شوند. این دو نقطه، نقاط شکست تابع احتمال نیز می‌شوند. به این ترتیب می‌توان نوشت: $$f_X(b)=f_X(c)=mode$$.

نکته: ممکن است در حالت کلی برای توزیع ذوزنقه‌ای، مقدار تابع احتمال در نقطه $$b$$ و $$c$$ یکسان نباشد. یعنی $$f_X(b)>f_X(c)$$ یا $$f_X(b)$$. چنین توزیعی را توزیع ذوزنقه‌ای تعمیم یافته (Generalized Trapezoidal Distribution) می‌نامند.

امید ریاضی

امید ریاضی برای متغیر تصادفی $$X$$ با توزیع ذوزنقه‌ای مطابق با رابطه زیر محاسبه می‌شود.

$$\large E(X)=\frac {1}{3(d+c-b-a)}\Big({\frac {d^{3}-c^{3}}{d-c}}-{\frac {b^{3}-a^{3}}{b-a}}\Big)$$

حالت خاص

در توزیع ذوزنقه‌ای، اگر پارامترهای $$a=b$$ و $$c=d$$ باشد، توزیع ذوزنقه‌ای تبدیل به توزیع یکنواخت در فاصله $$a$$ و $$d$$ می‌شود. همچنین با در نظر گرفتن $$b=c$$ نیز توزیع احتمال، به توزیع مثلثی تبدیل خواهد شد.

کاربردها

از آنجایی که توزیع‌های دیگر مانند توزیع نرمال می‌توانند تقریب خوب و مناسبی برای توزیع ذوزنقه‌ای باشند، کمتر به این توزیع توجه شده است. از طرفی بیشتر پدیده‌های تصادفی از گروه توزیع‌های غیرذوزنقه‌ای هستند.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• آزمایش تصادفی، پیشامد و تابع احتمال
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده

^^