مثلث، تعریف و محاسبات آن در هندسه – به زبان ساده
مثلث شکلی است که از سه ضلع و سه زاویه تشکیل شده است، بهطوریکه حاصلجمع این سه زاویه همیشه عدد ۱۸۰ خواهد بود.


مثلث متساویالاضلاع، متساویالساقین و اسکالن
مثلثها بر اساس اندازه اضلاع (یا اندازه زوایای داخلی) به سه دسته تقسیم میشوند.
در هر مثلث میتوان دو یا سه ضلع یا زاویه مساوی داشت یا میتوان هیچ ضلع و زاویه مساوی نداشت. به اشکال زیر توجه کنید.
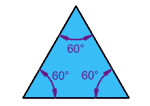
مثلث متساویالاضلاع
هر سه ضلع هماندازه هستند.
هر سه زاویه هماندازه و ۶۰ درجه هستند.
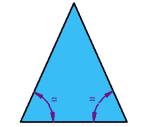
مثلث متساوی الساقین
دو ضلع هماندازه هستند.
دو زاویه هماندازه هستند.
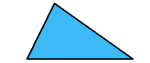
مثلث اسکالن
هیچکدام از اضلاع هماندازه نیستند.
هیچکدام از زوایا هماندازه نیستند.
مثلثها از نظر زوایا چگونه هستند؟
مثلثها براساس زوایا نیز دارای نامگذاریهای متفاوتی هستند.
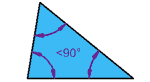
مثلث حاده
تمامی زوایای داخلی کمتر از 90 درجه هستند.
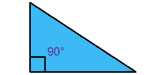
مثلث قائمالزاویه
یکی از زوایای داخلی 90 درجه است.
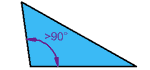
مثلث منفرجه
یکی از زوایای داخلی بیشتر از 90 درجه است.
مخلوطی از نامها
گاهی اوقات یک مثلث میتواند دو اسم داشته باشد، برای مثال
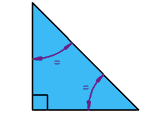
مثلث قائمالزاویه متساویالساقین
دارای یک زاویه قائمه (90درجه) است و سایر زوایا نیز با هم برابر هستند.
(میتوانید حدس بزنید اندازه سایر زوایا چند درجه است؟)
محیط مثلث
محیط یک مثلث مجموع اندازه اضلاع آن مثلث است. برای به دست آوردن محیط مثلث تنها کافی است اندازه اضلاع را با یکدیگر جمع کنید.
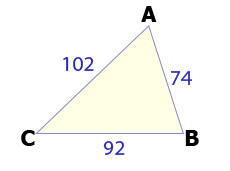
268 = 92 + 102 + 74 = محیط
مساحت مثلث
مساحت یک مثلث برابر است با حاصلضرب قاعده در ارتفاع، تقسیم بر 2.
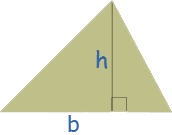
«b» طول ضلع و «h» ارتفاع مثلث (که از رأس زاویه عمود تا ضلع محاسبه میشود.) است.
مساحت = ½ × قاعده × ارتفاع
این فرمول برای تمامی مثلثها یکسان است.
نکته: برای سادهنویسی این فرمول، آن را به شکل زیر مینویسیم
b.h/2
مثال: مساحت مثلث زیر چقدر است؟
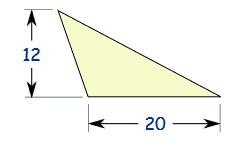
(نکته: عدد 12 ارتفاع مثلث است نه طول ضلع چپ)
ارتفاع h = 12
قاعده b = 20
2 / (قاعده × ارفتاع) = مساحت
120 = 2 / (12 × 20) = مساحت
توجه داشته باشید که از هر ضلعی میتوان به عنوان قاعده استفاده کرد، فقط باید مطمئن باشید که ارتفاع را از زاویهای در نظر بگیرید که به قاعده عمود است. جهت آشنایی بیشتر با محاسبه مساحت مثلثت به مقاله «مساحت مثلث -- به زبان ساده» مراجعه فرمایید.
(نکته: میتوان مساحت مثلث را با استفاده از فرمول هرون، از طریق طول اضلاع هم محاسبه کرد.)
اثبات
آیا برایتان این سؤال ایجاد شده است که چرا مساحت مثلث از فرمول نصف حاصلضرب قاعده در ارتفاع محاسبه میشود؟
خیلی سادهاست! فرض کنید یک مثلث به همان اندازه در کنار مثلث خودتان اضافه کردید. ( به صورت آینهوار و برعکس در کنار یکی از اضلاع بالایی) تا تقریباً یک متوازیالاضلاع درست شود. با کمی تغییر ساده میتوان آن را تبدیل به یک مستطیل کرد.
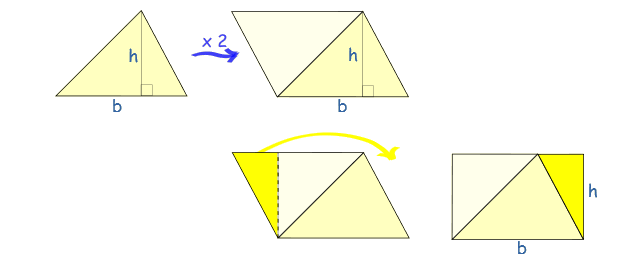
در این صورت، مساحت شکل حاصل برابر است با حاصلضرب ارتفاع در قاعده که این عدد، مساحت مجموع دو مثلث است.
حالا برای اینکه مساحت یک مثلث به دست بیاید، عدد بهدستآمده تقسیم بر دو میشود، یعنی همان b.h/2.












یعنی اگر از راس خطی عمود کنیم تا به ضلع برسد اون ارتفاع؟
سلام. بله، طبق تعریف، ارتفاع پارهخطی است که از یک رأس آغاز میشود و بر ضلع مقابل مثلث (یا امتداد آن) عمود است.
خسته نباشید اگر قاعده و یکی از اضلاع مثلثی یک عدد مساوی باشند،زاویه بین اضلاع چطور میشه؟ قانون خاصی داره؟؟
تو کتابم نوشته سینوس زاویه ای این دو ضلع برابر 1/2 است و من متوجه نمیشم..،ممنونم
سلام
ممنون،مفید بود و کمکم کرد.
خوب وکافی وکاربردی بود ممنون
من گسترده تراز این اطلاعات میخواستم مثلا دو ضلع و یه زاویه رو داریم مساحت مثلثو میخواهیم
رابطه زاویه ها با اضلاع
متشکرم خیلی عالی و شیوا بیان شده بود
ممنون عالی بود ساده ، روان و جذاب بیان شده مرسی
ممنون خوب بود
عالی بود مرسی