تحلیل پیچش در لوله های جدار نازک – آموزش جامع

در مباحث «پیچش و تغییر شکل‌های ناشی از آن» و «تحلیل میله‌های تحت پیچش»، به معرفی مفاهیم اساسی پیچش و مؤلفه‌های آن در میله‌ها و لوله‌های دایره‌ای پرداختیم اما تأثیر ضخامت و شکل سطح مقطع لوله‌ها بر روی مؤلفه‌های پیچش را مورد بررسی قرار ندادیم. در این مقاله، به ارائه روابط مناسب برای تعیین تنش برشی، انرژی کرنشی و زاویه پیچش در لوله‌های جدار نازک خواهیم پرداخت. در انتها نیز، به منظور آشنایی با نحوه به کارگیری روابط به دست آمده، چند مثال را تشریح خواهیم کرد.

تنش‌های برشی و جریان برش

به منظور آشنایی با نحوه تعیین روابط قابل استفاده برای لوله‌های جدار نازک با مقاطع مختلف، شکل زیر را در نظر بگیرید. ضخامت سطح مقطع این لوله (t) لزوماً ثابت نیست و امکان تغییر آن در بخش‌های مختلف وجود دارد.

با این وجود، مقدار t باید در مقایسه با عرض لوله کوچک باشد. با اعمال گشتاور پیچشی T بر روی دو انتهای لوله، جسم در معرض پیچش خالص قرار می‌گیرد. این کار باعث ایجاد تنش برشی درون لوله می‌شود.

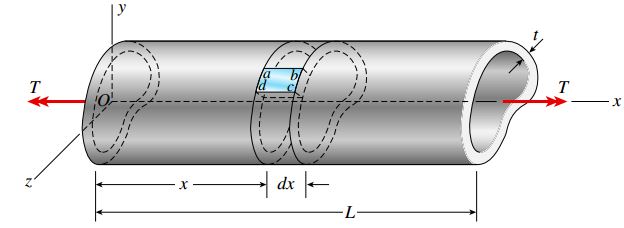
شکل زیر، تنش‌های برشی τ اعمال شده بر روی یک مقطع عرضی از لوله را نمایش می‌دهد. این تنش‌ها در جهت موازی با مرزهای سطح مقطع اعمال می‌شوند و در اطراف آن جریان می‌یابند. به دلیل فرض جدار نازک بودن لوله، مقدار تغییر شدت تنش‌ها در امتداد ضخامت آن بسیار کم است. به همین دلیل می‌توان مقدار τ در راستای مذکور را ثابت در نظر گرفت. اگر ضخامت لوله ثابت نباشد، شدت تنش بر روی نقاط مختلف مقطع عرضی متفاوت خواهد بود. در این حالت، باید الگوی تغییرات شدت تنش را با استفاده از معادلات تعادل به دست آورد.

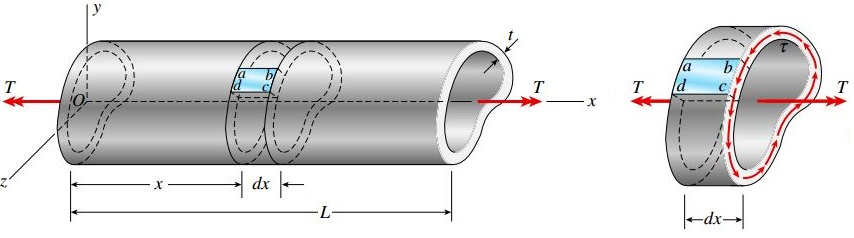
به منظور تعیین مقدار تنش‌های برشی، المان قرار گرفته در بین دو مقطع با فاصله dx از یکدیگر را در نظر بگیرید (المان abcd در شکل زیر). اگر شدت تنش‌های موجود بر روی این المان از b تا c تغییر کنند، تنش برشی موجود در b با عنوان τ_b و تنش برشی موجود در c با عنوان τ_c مشخص می‌شوند.

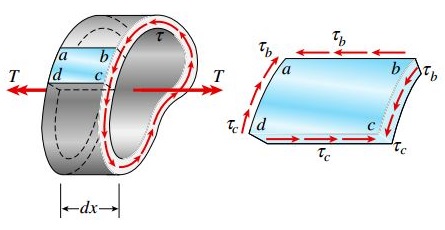
با در نظر گرفتن شرایط تعادلی برای المان مورد بررسی، تنش‌های برشی مشابه ای بر روی مقاطع رو به رویی، یعنی ad و bc اعمال خواهد شد. مقدار تنش‌های موجود بر روی این مقاطع با مقدار تنش‌های اعمال شده بر روی ab و cd برابر خواهد بود. به این ترتیب، تنش‌های برشی اعمال شده بر روی صفحات طولی ab و cd به ترتیب برابر با τ_b و τ_c است. این تنش‌ها باعث ایجاد نیروهای F_b و F_c می‌شوند.

مقدار نیروهای اعمال شده بر روی صفحات المان abcd از طریق روابط زیر به دست می‌آید:

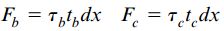
τ_b و τ_c به ترتیب ضخامت لوله در نقاط b و c را نمایش می‌دهند. نیروهای F₁ توسط تنش‌های اعمال شده بر روی صفحات bc و ad به وجود می‌آیند. با در نظر گرفتن تعادل المان در راستای طولی (محور x)، رابطه F_b=F_c برقرار خواهد بود. این رابطه را می‌توان به صورت زیر نیز بیان کرد:

به دلیل انتخاب اختیاری محل قرارگیری مقاطع طولی ab و cd، رابطه بالا (حاصل‌ضرب تنش برشی در ضخامت لوله) برای تمام نقاط سطح مقطع یکسان خواهد بود. این رابطه با عنوان «جریان برش» (Shear Flow) شناخته شده و با حرف f نمایش داده می‌شود:

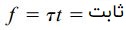
بر اساس این رابطه، بزرگ‌ترین تنش برشی در کوچک‌ترین ضخامت و کوچک‌ترین تنش برشی در بزرگ‌ترین ضخامت رخ می‌دهد. در محدوده‌هایی که ضخامت لوله ثابت است، تنش برشی نیز ثابت خواهد بود. توجه داشته باشید که جریان برش، نیروی برشی در واحد ضخامت سطح مقطع را نمایش می‌دهد.

رابطه پیچش برای لوله‌های جدار نازک

قدم بعدی در تحلیل لوله‌های جدار نازک، مشخص کردن رابطه بین جریان برش و گشتاور پیچشی است. به این منظور، سطح مقطع نمایش داده شده در بخش قبلی را مورد بررسی قرار می‌دهیم (شکل زیر). خط میانی جداره لوله با خط‌چین نمایش داده شده است.

اکنون، بخشی از سطح مقطع مورد بررسی با طول ds و ضخامت t را در نظر بگیرید. فاصله s، موقعیت المان در نظر گرفته شده تا یک نقطه مرجع دلخواه را نمایش می‌دهد.

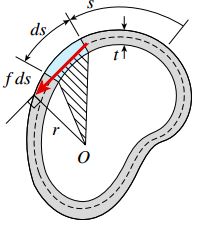
نیروی برشی کل بر روی المان سطح برابر با fds است. گشتاور این نیرو حول نقطه O به صورت زیر تعیین می‌شود:

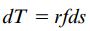
r، فاصله عمودی از نقطه O تا خط اثر نیروی fds را نمایش می‌دهد. توجه داشته باشید که خط اثر fds بر روی خط میانی سطح مقطع در المان ds مماس است. گشتاور پیچشی ناشی از تنش‌های برشی با انتگرال‌گیری بر روی محدوده خط میانی سطح مقطع به دست می‌آید:

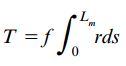
L_m: طول خط میانی

در برخی از موارد، انتگرال‌گیری از رابطه بالا بسیار دشوار است اما خوشبختانه این مشکل با استفاده از ساده‌سازی‌های هندسی برطرف می‌شود. کمیت rds، دو برابر مساحت مثلث هاشور خورده در شکل زیر را نمایش می‌دهد. توجه داشته باشید که قاعده این مثلث برابر با ds و ارتفاع آن برابر با r است.

به این ترتیب، انتگرال کل، دو برابر مساحت به دست آمده از منحنی بسته خط میانی (A_m) خواهد بود:

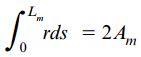
با توجه به رابطه قبلی، به رابطه T=2fA_m می‌رسیم. بنابراین، جریان برشی برابر است با:

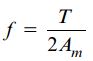
اگر f=τt را درون رابطه بالا قرار دهیم، به رابطه پیچش برای لوله‌های جدار نازک دست می‌یابیم:

t: ضخامت جدار لوله؛ A_m: مساحت سطح مقطع (با توجه به خط میانی)؛ τ: تنش‌های برشی؛ T: گشتاور پیچشی

برای نمایش کاربرد رابطه پیچش، یک لوله جدا نازک دایره‌ای با ضخامت t و شعاع r نسبت به خط میانی را در نظر بگیرید.

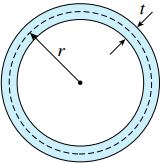
مساحت ناحیه به وجود آمده توسط خط میانی برابر است با:

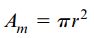
با توجه به این رابطه، تنش برشی به صورت زیر تعیین می‌شود:

رابطه بالا مشابه رابطه پیچش در یک لوله دایره‌ای با دیواره نازک است. برای بررسی حالت‌های دیگر، یک لوله جدار نازک با سطح مقطع مستطیلی شکل، ضخامت t₁ در کناره‌ها و ضخامت t₂ در بالا و پایین را در نظر بگیرید. ارتفاع و عرض این لوله (با توجه به خط میانی سطح مقطع) به ترتیب برابر با h و b است.

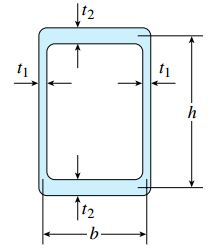
مساحت ناحیه داخل خط میانی سطح مقطع به صورت زیر تعیین می‌شود:

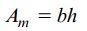
تنش‌های برشی در صفحات عمودی و افقی لوله نیز به صورت زیر به دست می‌آیند:

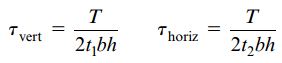
τ_ver: تنش برشی عمودی؛ τ_horiz: تنش برشی افقی؛ t₁: ضخامت بخش‌های کناری؛ t₂: ضخامت بخش‌های بالایی و پایینی

اگر t₂ از t₁ بزرگ‌تر باشد، تنش برشی ماکسیمم در بخش‌های عمودی سطح مقطع رخ می‌دهد.

انرژی کرنشی و ثابت پیچش

با استفاده از تعیین انرژی کرنشی یک المان و انتگرال‌گیری در محدوده آن می‌توان انرژی کرنشی یک لوله جدار نازک را محاسبه کرد. المانی با مساحت سطح مقطع tds و طول dx را در نظر بگیرید. حجم این المان برابر با tdsdx است (مشابه حجم المان abcd در بخش اول مقاله). به دلیل قرار داشتن لوله در معرض برش خالص، چگالی انرژی کرنشی المان برابر با τ²/2G خواهد بود.

به این ترتیب، انرژی کرنشی کل از ضرب چگالی انرژی کرنشی در حجم به دست می‌آید:

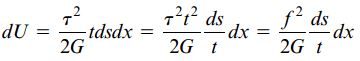
به جای عبارت τt در رابطه بالا از کمیت جریان برش f به عنوان یک پارامتر ثابت استفاده شده است. برای تعیین انرژی کرنشی کل لوله باید از du انتگرال‌گیری کنیم. به این منظور، از ds در محدوده 0 تا L_m (طول خط میانی) و از dx در محدوده 0 تا L (طول لوله) انتگرال می‌گیریم. به این ترتیب:

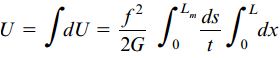
توجه داشته باشید که ضخامت t می‌تواند در اطراف خط میانی تغییر می‌کند. از این‌رو، کمیت مذکور باید به همراه ds در انتگرال قرار داشته باشد. حاصل انتگرال آخر در رابطه بالا با طول لوله برابر است. به همین دلیل، رابطه انرژی کرنشی به صورت زیر درمی‌آید:

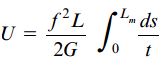
با جایگذاری رابطه جریان برش در این رابطه، خواهیم داشت:

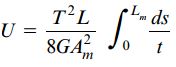
این جایگذاری به منظور بازنویسی رابطه انرژی کرنشی بر حسب گشتاور پیچشی T صورت می‌گیرد. عبارت بالا را می‌توان به فرم ساده‌تری تبدیل کرد. این کار با معرفی یک ویژگی جدید به نام «ثابت پیچش» (Torsion Constant) صورت می‌گیرد. ثابت پیچش، یکی از ویژگی‌های سطح مقطع جسم به شمار می‌رود. برای یک لوله جدار نازک، این ثابت به صورت زیر تعریف می‌شود:

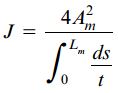
با در نظر گرفتن مفهوم ثابت پیچش، معادله انرژی کرنشی به فرم زیر درمی‌آید:

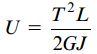
این رابطه با رابطه معرفی شده برای تعیین انرژی کرنشی یک لوله دایره‌ای شکل شباهت دارد. تنها تفاوت بین این دو رابطه، قرارگیری ثابت پیچش J به جای ممان اینرسی قطبی I_p است. توجه داشته باشید که ثابت پیچش بر حسب واحد طول به توان چهار بیان می‌شود. اگر ضخامت سطح مقطع لوله ثابت باشد، رابطه J ساده‌تر خواهد شد:

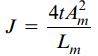
با استفاده روابط معرفی شده برای J می‌توانیم ثابت پیچش سطح مقطعی با هر شکل دلخواه را محاسبه کنیم. لوله جدار نازک دایره‌ای زیر را در نظر بگیرید. به دلیل ثابت بودن ضخامت، از رابطه بالا برای تعیین ثابت پیچش استفاده می‌کنیم.

با جایگذاری L_m=2πr و A_m=πr² به رابط زیر می‌رسیم:

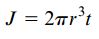
این رابطه، با رابطه تقریبی ممان اینرسی قطبی برابر است. بنابراین، در لوله‌های جدار نازک دایره‌ای، ممان اینرسی قطبی با ثابت پیچش برابر خواهد بود. اکنون یک لوله مستطیلی مطابق شکل زیر را در نظر بگیرید.

برای این لوله، A_m=bh است. بنابراین، انتگرال موجود در رابطه ثابت پیچش آن به صورت زیر حل می‌شود:

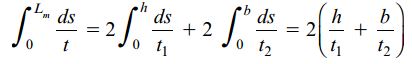
به این ترتیب، رابطه ثابت پیچش لوله جدار نازک مستطیلی با ضخامت ثابت برابر است با:

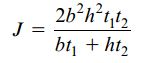
ثابت پیچش لوله‌های جدار نازک با سطح مقطع‌های دیگر نیز به همین ترتیب تعیین می‌شوند.

زاویه پیچش

زاویه پیچش φ یک لوله جدار نازک با سطح مقطع دلخواه از طریق تعیین رابطه کار انجام شده توسط گشتاور اعمال شده و برابر قرار دادن آن با رابطه انرژی کرنشی لوله نیز به دست می‌آید.

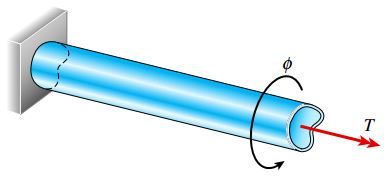
بنابراین:

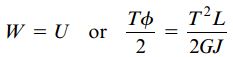
به این ترتیب، رابطه زاویه پیچش به صورت زیر نوشته می‌شود:

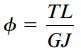
این رابطه نیز با معادله مربوط به زاویه پیچش لوله‌های دایره‌ای شباهت دارد. تفاوت این دو رابطه نیز در قرارگیری J به جای I_p است. کمیت GJ با عنوان «صلبیت پیچشی» (Torsional Rigidity) شناخته می‌شود.

نکات تکمیلی

روابطی که در این مقاله معرفی کردیم، برای عضوهای منشوری (سطح مقطع یکنواخت در راستای محور طولی) با شکل بسته و دیواره نازک کاربرد دارند. اگر سطح مقطع به صورت جدار نازک اما باز باشد (مانند تیرهای I شکل)، روابط ارائه شده معتبر نخواهند بود. برای درک بیشتر اهمیت این موضوع، یک لوله جدار نازک را در نظر بگیرید. در صورت ایجاد برش طولی در این لوله، سطح مقطع آن باز خواهد شد. در این حالت، تنش‌های برشی و زوایای پیچش افزایش می‌یابند. علاوه بر این، مقاومت پیچشی لوله نیز کمتر می‌شود. به این ترتیب، روابط قبلی دیگر برای این شرایط قابل استفاده نیستند. به منظور ارزیابی وضعیت مذکور باید از تئوری‌های پیشرفته‌تر برای تعیین روابط تنش برشی و زاویه پیچش استفاده کرد.

برخی از روابط معرفی شده در این مقاله تنها برای مواد الاستیک خطی کاربرد دارند. به عنوان مثال، روابطی که دارای کمیت مدول برشی G هستند، در این گروه قرار می‌گیرند. با این وجود، معادلات جریان برش و تنش برشی صرفاً از طریق معادلات تعادل به دست آمده‌اند. به همین دلیل، این معادلات برای تمامی مواد با هر خصوصیاتی قابل استفاده خواهند بود. مباحث تئوری ارائه شده، تخمینی از مؤلفه‌های پیچش برای لوله‌های جدار نازک را فراهم می‌کنند. از آنجایی که این تئوری با در نظر گرفتن خطوط میانی سطح مقطع لوله گسترش یافته است، افزایش ضخامت دیواره باعث کاهش دقت روابط خواهد شد.

یکی از ملاحظات قابل توجه در طراحی لوله‌های جدا نازک، در نظر گرفتن مسئله «کمانش» (Buckling) است. هر چه لوله نازک‌تر و طول آن زیادتر باشد، احتمال رخ دادن کمانش افزایش می‌یابد. در لوله‌های غیر دایره‌ای، اغلب از تقویت‌کننده‌ها و دیافراگم‌های مخصوص برای جلوگیری از تغییر شکل لوله در نواحی ضعیف استفاده می‌شود. در این مقاله، فرض می‌کنیم که هیچ کمانشی در مباحث و مثال‌های ارائه شده وجود نخواهد داشت.

مثال‌ها

به منظور آشنایی با نحوه به کارگیری روابط معرفی شده برای تحلیل مؤلفه‌های پیچش در لوله‌های جدار نازک، دو مثال را برای شما تشریح خواهیم کرد.

مثال 1

لوله دایره‌ای نمایش داده شده در شکل زیر را در نظر بگیرید. مقدار تنش برشی ماکسیمم حاصل از روش تقریبی برای لوله‌های جدار نازک را با مقدار به دست آمده از رابطه پیچش مقایسه کنید. توجه داشته باشید که ضخامت سطح مقطع و فاصله شعاعی خط میانی آن تا مرکز لوله ثابت است.

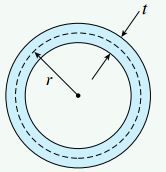
روش تقریبی

رابطه مورد نیاز برای محاسبه تنش برشی با استفاده از روش تقریبی به صورت زیر است:

در این رابطه:

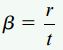
رابطه پیچش

برای محاسبه تنش برشی ماکسیمم از طریق رابطه پیچش، داریم:

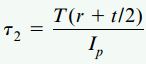
که در آن:

اگر رابطه بالا را باز کنیم، به فرم ساده شده زیر می‌رسیم:

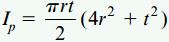
به این ترتیب، رابطه تنش برشی به شکل زیر درمی‌آید:

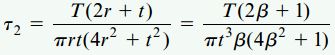
مقایسه روابط

نسبت تنش‌های برشی به دست آمده از دو روش بالا برابر است با:

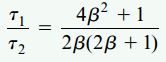
این نسبت، تنها به کمیت β بستگی دارد.

تحلیل نتیجه به دست آمده

اگر مقادیر β را به ترتیب برابر با 5، 10 و 20 قرار دهیم، نسبت τ₁/τ₂ به ترتیب برابر با 0.92، 0.95 و 0.98 خواهد شد. با توجه به این مقادیر می‌توان مشاهده کرد که مقادیر به دست آمده از رابطه تقریبی اختلاف بسیار کمی با رابطه پیچش دارند. با کاهش ضخامت دیواره لوله، دقت روش تقریبی افزایش می‌یابد. هنگامی که ضخامت دیواره لوله به صفر و β به بی‌نهایت میل کند، نسبت τ₁/τ₂ به مقدار 1 خواهد رسید.

مثال 2

شکل زیر، یک لوله با مقطع دایره‌ای و یک لوله با مقطع مربعی را نمایش می‌دهد. این دو لوله در معرض گشتاور پیچشی برابر قرار دارند. اگر ماده تشکیل‌دهنده، طول، ضخامت دیواره و مساحت سطح مقطع هر دو آن‌ها یکسان باشد، نسبت تنش‌های برشی و همچنین نسبت زوایای پیچش به وجود آمده چقدر خواهد بود؟ (از تمرکز تنش در گوشه‌های لوله مربعی صرف‌نظر کنید.)

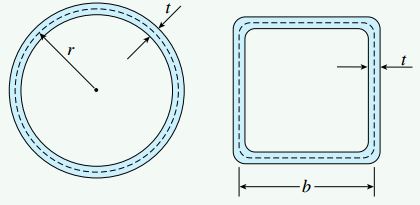
لوله دایره‌ای

مساحت ناحیه بسته حاصل از خط میانی سطح مقطع لوله (خط‌چین) از طریق رابطه زیر به دست می‌آید:

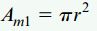
r، فاصله شعاعی مرکز میله تا خط میانی سطح مقطع را نمایش می‌دهد. ثابت پیچش و مساحت مقطع عرضی نیز با استفاده از روابط زیر تعیین می‌شوند:

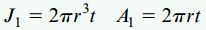
لوله مربعی

برای لوله مربعی، مساحت مقطع عرضی برابر است با:

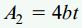
b، طول یکی از اضلاع خط میانی سطح مقطع لوله (خط‌چین) است. به دلیل برابر بودن مساحت لوله‌ها (4bt=2πrt)، طول ضلع مذکور b=πr/2 خواهد بود. ثابت پیچش و مساحت ناحیه بسته حاصل از خط میانی در لوله مربعی نیز به صورت زیر محاسبه می‌شود:

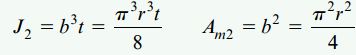
نسبت‌های تنش برشی و زوایای پیچشی

با توجه به رابطه پیچش لوله‌های جدار نازک، نسبت τ₁/τ₂ به صورت زیر به دست می‌آید:

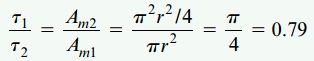
با استفاده از رابطه گشتاور-جابجایی φ=TL/GJ نیز نسبت زوایای پیچش قابل تعیین خواهد بود:

نتایج به دست آمده نشان می‌دهند که لوله دایره‌ای نسبت به لوله مربعی، علاوه بر کمتر بودن 21 درصدی مقدار تنش برشی، از بیشتر بودن مقاومت در برابر پیچش نیز بهره می‌برد.

^^