تحلیل سری زمانی با پایتون – معرفی انواع مدل ها

تحلیل سری زمانی و انتخاب مدل مناسب برای تحلیل آن‌ها یکی از مهم‌ترین بخش‌های تجزیه و تحلیل داده‌های مرتبط با زمان است. انجام محاسبات و رسم نمودارها، از وظایف اصلی «تحلیل‌گر داده» (Data Scientist) محسوب می‌شود. زبان برنامه نویسی پایتون از ابزارهای مفید در این امر است. در سری مطالب دنباله‌ای تحلیل سری زمانی با پایتون، در قسمت اول، به بررسی مفاهیم اولیه در مبحث سری زمانی پرداختیم. در این بخش، مدل‌های پایه برای سری زمانی و نحوه ایستا کردن (Stationary)  آن‌ها را مرور خواهیم کرد. در بخش آخر و سوم، به معرفی مدل‌های ترکیبی و پیچیده سری زمانی خواهیم پرداخت و پیاده‌سازی چنین مدل‌هایی را با زبان برنامه‌نویسی پایتون فرا خواهیم گرفت.

تحلیل سری زمانی با پایتون به صورت دنباله‌ای از نوشتارها در سه بخش ارائه می‌شود.

• بخش نخست: تحلیل سری زمانی با پایتون --- مقدمات و مفاهیم اولیه
• بخش دوم: تحلیل سری زمانی با پایتون --- معرفی انواع مدل‌ها
• بخش سوم: تحلیل سری زمانی با پایتون --- مدل‌های ترکیبی و پیچیده

برای آشنایی بیشتر با مقدمات مربوط به مبحث سری زمانی بهتر است نوشتار تحلیل سری زمانی — تعریف و مفاهیم اولیه را بخوانید. همچنین خواندن مطلب سری زمانی در علم داده — از صفر تا صد نیز خالی از لطف نیست.

تحلیل سری زمانی و معرفی انواع مدل‌ها

همانطور که در بخش اول از این سری مطالب مطالعه کردید، مدل خطی یکی از انواع مدل‌های سری زمانی است که در آن بوسیله رابطه خطی داده‌ها با زمان، عمل مدل‌سازی صورت می‌گیرد. ولی متاسفانه، مدل ساخته شده دارای خاصیت ایستایی (Stationary) نیست. در ادامه به معرفی مدل‌هایی خواهیم پرداخت به صورت خطی بوده و خاصیت ایستایی نیز دارند.

مدل خودهمبسته

زمانی که متغیر وابسته با مقدارهایی از خودش (با در نظر گرفتن مقدار تاخیر مناسب) تشکیل یک مدل خطی دهد، مدل را «خودهمبسته» (Autoregressive) می‌نامند.  شیوه نمایش چنین مدلی به زبان ریاضی به صورت زیر خواهد بود.

$$\large x_t=a_1x_{t-1}+\cdots a_px_{t-p}+w_t\\ \large = \sum_{i=1}^pa_ix_{t-i}+w_t$$

چنین مدلی را با نماد $$AR(p)$$ نشان می‌دهند. به مانند مدل‌های دیگر $$w_t$$‌ میزان خطا یا نویز سفید در مدل است. همچنین $$p$$ را مرتبه مدل «اتورگرسیو» یا «خودهمبسته» می‌نامند. به این ترتیب مشخص است که منظور از $$p$$ میزان تاخیراتی است که باید در مدل لحاظ شود. با توجه به مقدار $$p$$ تعداد داده‌هایی که از گذشته روی متغیر $$x$$ در زمان $$t$$ تاثیرگذار هستند مشخص می‌شود. برای مثال مدل $$AR(2)$$ به صورت زیر نوشته خواهد شد.

$$\large x_t=a_1x_{t-1}+a_2x_{t-2}+w_t, \;\;a_1, a_2 \neq 0$$

این مدل نشان می‌دهد که مقدار متغیر در زمان $$t$$ به مقدار متغیر در زمان‌های $$t-1$$و $$t-2$$ وابسته است و مدل این وابستگی نیز خطی است. از طرفی مقدار خطا یا نویز سفید $$w_t$$ نیز در مقدار $$x_t$$ نقش دارد.

نکته: اگر در مدل $$AR(1)$$ مقدار $$a_1=1$$ باشد، مدل به صورت قدم‌های تصادفی در خواهد آمد. در قسمت اول از مطالب دنباله‌ای سری زمانی، مشخص شد که چنین مدلی ایستا نیست.

$$\large x_t=x_{t-1}+w_t$$

با استفاده از کد زیر به شبیه‌سازی داده‌های چنین مدلی خواهیم پرداخت. در اینجا ضریب ($$a_1$$) برابر با 0.6 در نظر گرفته شده است.

نمودارهای تحلیل سری زمانی مربوط به چنین داده‌هایی در ادامه قابل مشاهده است. این نمودارها الگوی مناسبی برای تشخیص داده‌های سری زمانی با مدل $$AR(1)$$ هستند. به این معنی که اگر برای یک سری داده، نمودارهای سری زمانی ترسیم شود و الگوی مشابه با نمودارهای زیر داشته باشد می‌توان آن را سری زمانی با مدل $$AR(1)$$ در نظر گرفت.

نکته: تابع tsplot در بخش اول از این نوشتارها معرفی شده است.

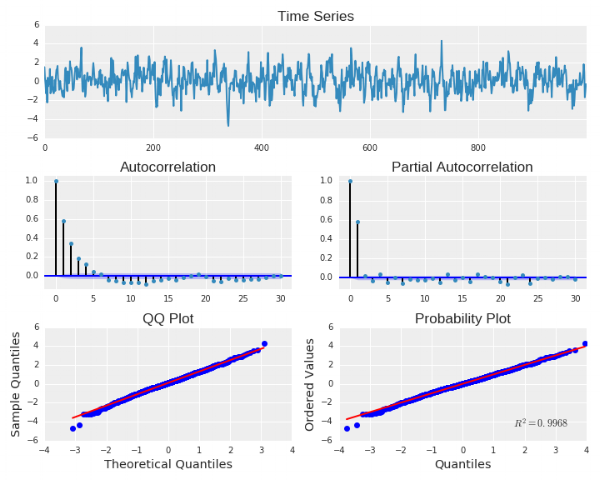
همانطور که انتظار داشتیم، توزیع باقی‌مانده‌ها نرمال است. از طرفی میزان همبستگی بین داده‌ها بخصوص در تاخیر اول (Lag 1) که در منحنی PACF دیده می‌شود، گواه وجود رابطه بین مشاهدات است. در ادامه یک مدل $$AR(p)$$ را به کمک توابع پایتون ایجاد می‌کنیم. ابتدا یک مدل $$AR$$ را برای داده‌ها در نظر می‌گیریم و ضریب $$a_1$$ را برآورد می‌کنیم. سپس به منظور برآورد مقدار $$p$$ از تابع select_order استفاده خواهیم کرد. اگر مقدار ضریب $$a_1$$ نزدیک به مقدار 0.6 برآورد شود، آنگاه به نظر می‌رسد مدل $$AR(1)$$ برای داده مناسب است.

کدهای زیر به این منظور تهیه شده‌اند. همانطور که مشخص است متغیر $$x$$‌ از قسمت قبلی که در آن شبیه‌سازی صورت گرفته بود، دریافت شده و برای برازش مدل سری زمانی استفاده شده است.

مقدارهای برآورد شده برای ضریب و تاخیر (lag) به صورت زیر است.

$$\large alpha\; estimate = 0.58227 \; | \; best\; lag\; order = 1\\ \large true\; alpha = 0.6 \;\;\; | true\; order = 1$$

به نظر می‌رسد که پارامتر واقعی مدل را به خوبی پیش‌بینی کرده‌ایم. حال به بررسی و شبیه‌سازی مدل $$AR(2)$$ می‌پردازیم. در ادامه کد مربوط به شبیه‌سازی چنین داده‌هایی نوشته شده است.

با توجه به داده‌های شبیه‌سازی شده، نمودارهای تحلیل سری‌زمانی با تابع tsplot، ترسیم شده است.

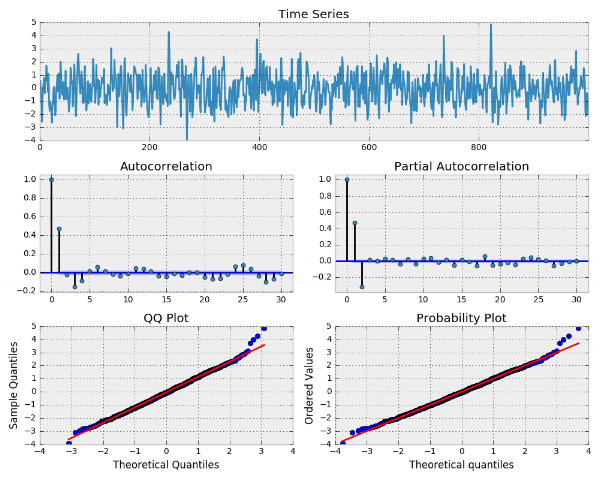
در این قسمت سعی می‌کنیم پارامتر مربوط به داده‌های شبیه‌سازی شده را برآورد کنیم. مدل در نظر گرفته شده توسط تابع select_order در اینجا هم برابر با ۲ است.

خروجی‌های که در ادامه قابل مشاهده هستند تقریبا برابر با ضریب‌های واقعی هستند.

$$\large coef\; estimate:\;0.6291\;\;-0.3196\;\;|\;\; best\; lag\;\;order\;=2\\ \large true\;\;coefs=[0.666,\;\;-0.333]\;|\;true\;order =2$$

به منظور بررسی مدل سری زمانی $$AR(1)$$ برای داده‌های MSFT که در بخش اول این سری مطالب معرفی و بارگذاری شده، دستور زیر را اجرا کنید.

حال به بررسی خروجی تابع tsplot برای لگاریتم داده‌های MSFT می‌پردازیم.

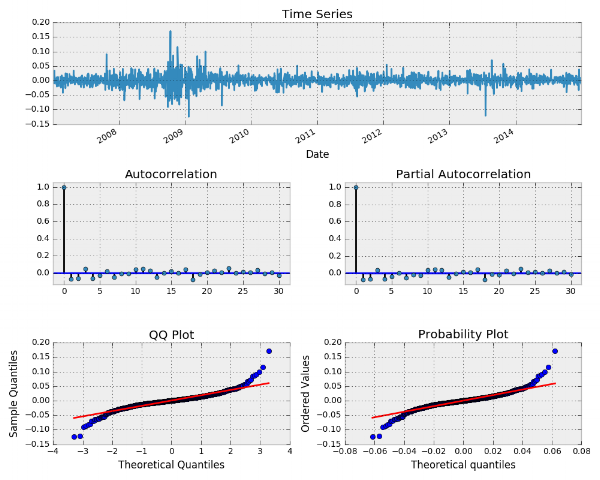
به نظر می‌رسد که خطا‌ها توزیع نرمال دارند ولی بعد از گذشت ۲۳ تاخیر ضریب خودهمبستگی ACF به صفر میل می‌کند. حال با اجرای کد زیر محاسبات مربوط به برازش سری زمانی طی کرده و نتایج را مورد بررسی قرار می‌دهیم.

نتیجه اجرای این کد به صورت زیر است:

$$\large best\;estimated\;lag\;order\;=23$$

به نظر می‌رسد که میزان تاخیر در این مدل برابر با ۲۳ است یا مدل دارای ۲۳ پارامتر خواهد بود. با توجه به تعدد پارامترها، مدل مناسب به نظر نمی‌رسد زیرا پیچیدگی آن زیاد است.

مدل میانگین متحرک (Moving Average)

مدل «میانگین متحرک» (Moving Average) با پارامتر $$q$$ مشخص می‌شود. این پارامتر نشان می‌دهد که مقدار سری زمانی در زمان $$t$$ با $$q$$ مقدار خطا یا نویز سفید تشکیل یک مدل خطی می‌دهد. از نظر اینکه مدل میانگین متحرک به صورت ترکیب خطی نوشته می‌شود، مشابه با مدل AR است ولی با این تفاوت که برحسب ترکیب خطی از خطاهای برحسب زمان، نوشته می‌شود.

فیلم آموزش روش های پارامتریک و غیر پارامتریک حذف گرایش یا Trend از سری های زمانی (رایگان) در فرادرس

کلیک کنید

بیان ریاضی برای مدل میانگین متحرک با توجه به نمادهای به کار رفته در قسمت اول به صورت زیر است.

$$\large x_t=w_t+\beta_1w_{t-1}+\cdots+\beta_pw_{t-q}=w_t+\sum_{i=1}^q\beta_iw_{t-i}$$

در اینجا $$w_t$$ همان نویز‌های سفید با میانگین صفر و ورایانس ۱ در زمان $$t$$ هستند.

نکته: از آنجایی که در کد زیر از تابع arma_generate_sample استفاده شده مقدار p در مدل AR را صفر در نظر گرفته‌ایم. مدل arma ترکیبی از مدل $$AR$$ و $$MA$$ است که اولین پارامتر آن $$p$$ و دومین نیز همان $$q$$‌ است.

خروجی این برنامه که توسط تابع tsplot ساخته شده و به صورت زیر است.

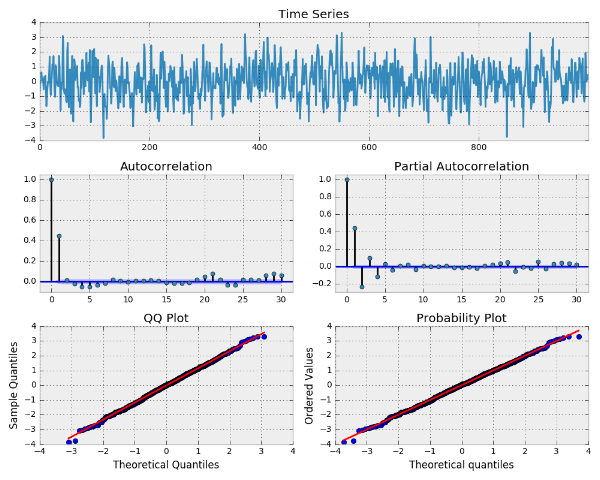
نمودار مربوط به تابع ACF بیانگر وجود تاخیر یا Lag=1 است که تاییدی برای استفاده از مدل $$MA(1)$$ است. باقی‌مانده‌ها نیز نرمال به نظر می‌رسند. کد زیر به منظور برازش مدل $$MA(1)$$ برای داده‌های شبیه‌سازی شده نوشته شده است.

خروجی این دستورات به صورت جدولی است که توسط تابع summary ایجاد می‌شود. به تصویر زیر توجه کنید.

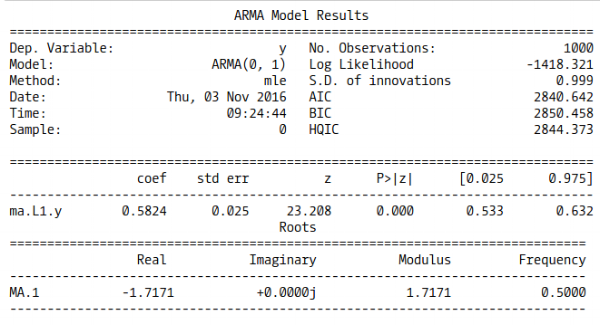
به نظر می‌رسد که مدل $$MA(1)$$ به خوبی با ضریب 0.58 برازش شده است که بسیار به مقدار 0.6 که برای شبیه‌سازی به کار رفته نزدیک است. از طرفی فاصله اطمینان برای پارامتر مدل شامل مقدار واقعی نیز هست. حال به بررسی مدل $$MA(3)$$ می‌پردازیم. ابتدا ۱۰0۰ مشاهده از چنین مدلی را شبیه‌سازی می‌کنیم. همانطور که مشخص است، در این مدل از سه ضریب و پارامتر (0.6, 0.4, 0.2) برای مدل استفاده خواهیم کرد.

نمودارهای مربوط به چنین مدلی به صورت زیر خواهند بود.

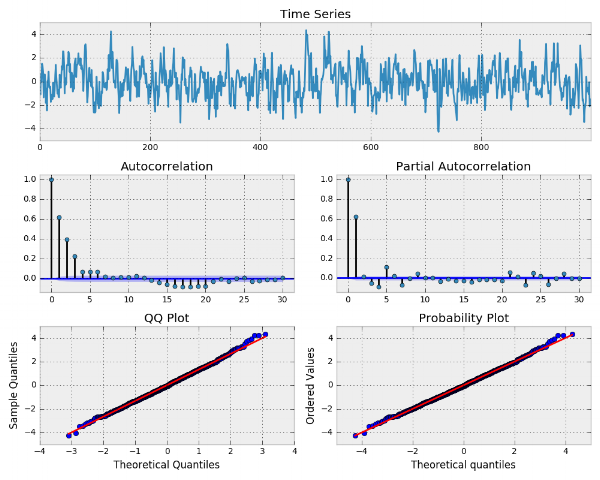
حال به بررسی نحوه برازش این داده‌ها توسط پایتون خواهیم پرداخت. به دستورات زیر توجه کنید. به نظر می‌رسد در ستون coef ضرایب به خوبی پیش‌بینی شده‌اند.

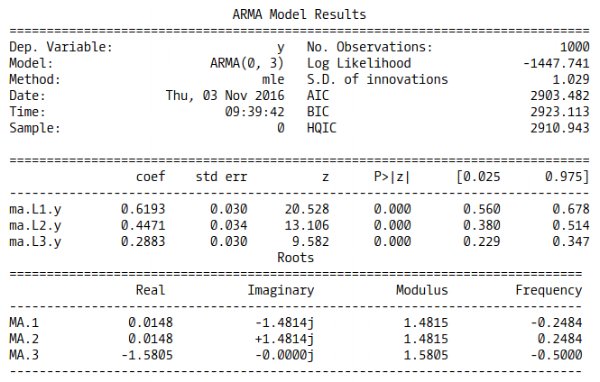
باز هم کاملا مشخص است که مدل به خوبی پارامترها را برآورد کرده است. فاصله اطمینان ۹۵٪ شامل مقدارهای واقعی پارامترها هستند. حال به منظور به کارگیری چنین مدلی روی داده‌های واقعی از مجموعه داده SPY استفاده خواهیم کرد. در این وضعیت اطلاعی از مقدار واقعی پارامترهای مدل $$MA(3)$$ برای این داده‌ها نداریم.

خروجی مدل برازش شده $$MA(3)$$ به صورت زیر است.

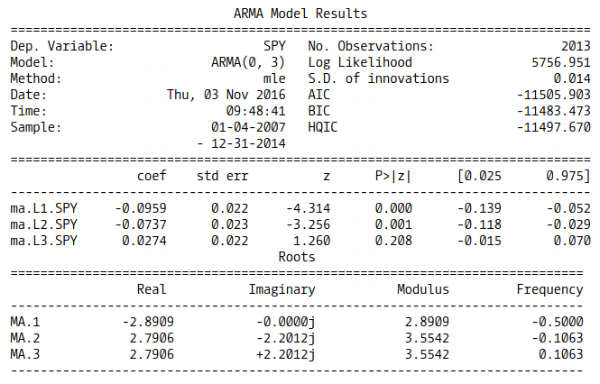
حال به بررسی نمودار تحلیل سری زمانی با تابع tsplot‌ می‌پردازیم.

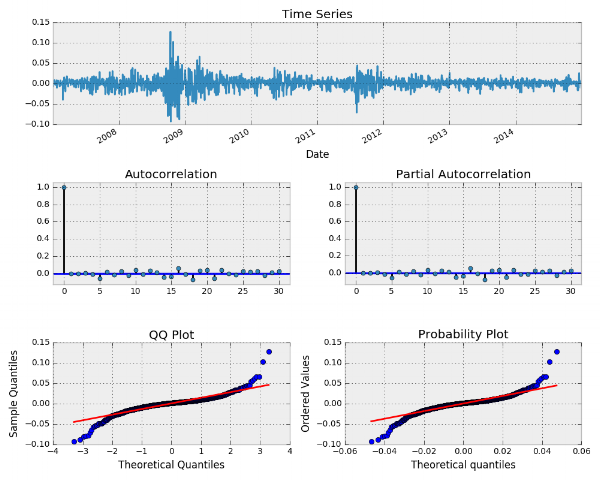
وجود نقاط پرت در نمودارهای Q-Q plot و P-P plot‌ می‌تواند بیانگر وجود مدل مناسب‌تر برای چنین داده‌هایی باشد. از طرفی نمودار ACF نیز در نقاط ۵ و ۱۶ و حتی ۱۸ مقدارهایی مخالف صفر دارند که به نظر مشکل‌ساز می‌رسند. در ادامه و در قسمت سوم از این نوشتارها، مدل‌های مناسب‌تر برای این داده‌ها معرفی خواهد شد.

در قسمت‌ اول از این دنباله مقالات، به معرفی مفاهیم اولیه و مدل‌های پایه برای سری زمانی پرداختیم. در قسمت دوم نیز بررسی مدل‌هایی پرداختیم که ایستا هستند. سپس برای سری‌های زمانی ناایستا به دنبال تبدیلاتی گشتیم که آن‌ها را تبدیل به مدل‌هایی ایستایی کنند. در قسمت سوم و آخر نیز به مدل‌های ترکیبی پیچیده در مبحث سری‌های زمانی خواهیم پرداخت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش تحلیل و پیش‌بینی سری های زمانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش های کاربردی شبکه های عصبی مصنوعی
• سری زمانی در علم داده — از صفر تا صد
• تحلیل سری زمانی — تعریف و مفاهیم اولیه

^^