توضیح توان و لگاریتم در ریاضیات – به زبان ساده
در این نوشته ترفندی برای تفکر در مورد مسائل ریاضی شامل توان و لگاریتم ارائه شده است. کافی است دو سؤال از خود بپرسید: آیا ما در مورد ورودیها (علت تغییر) صحبت میکنیم یا در مورد خروجیها (تغییر واقعی رخ داده)؟
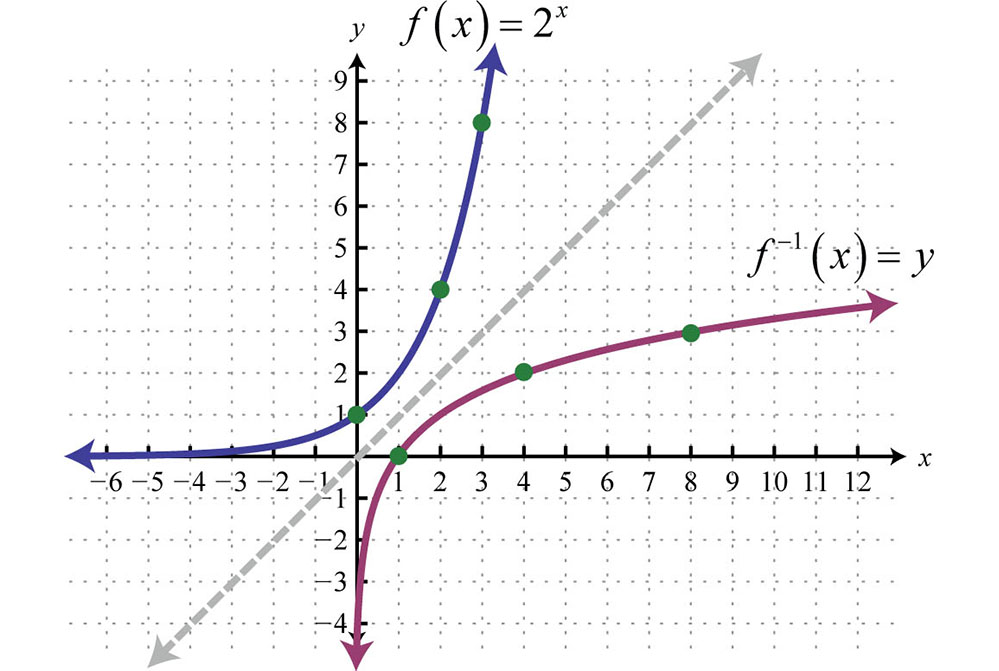
- لگاریتمها، ورودیهایی را نشان میدهند که موجب رشد میشوند.
- توانها نتیجه نهایی رشد را نمایان میکنند.
آیا ما در مورد چشمانداز رشد کننده صحبت میکنیم یا ناظر رشد؟
- e و لگاریتم طبیعی لحظه به لحظه از منظر رشد کننده رخ میدهند.
- مبنای 10، 20 و غیره معیارهایی هستند که محاسبات را برای ناظر انسانی تسهیل میکنند.
گزارههای فوق را میتوان در جدول زیر جمعبندی نمود:
| یافتن علت | یافتن تأثیر | |
|---|---|---|
| از منظر رشدکننده | (ln(x --- لگاریتم طبیعی | توان در مبنای e |
| از منظر ناظر رشد | و لگاریتمهای دیگر | و توانهای دیگر |
در واقع این طور میتوانیم واقعیتهای فوق را به خاطر بسپاریم که ما از منظر رشدکننده به علت نیاز داریم و به همین علت لگاریتم طبیعی است. دقت کنید که لگاریتم طبیعی با حروف اختصاری LN نمایش مییابد که از واژه لاتین logarithmus naturalis منشأ مییابد.
در برخی کلاسهای ریاضیات محتوای جدول فوق بدون هیچ توضیحی و صرفاً با عنوان کردن تابعهای محض و بدون حتی توضیح شیوه و محل استفاده از آنها ارائه میشوند. چنین رویهای مناسب نیست. در ادامه به توضیح عملی توان و لگاریتم میپردازیم.
توصیف رشد GDP
یک مثال نوعی از رشد به این صورت است: از سال 2000 تا 2010 GDP ایران از 109.6 میلیارد دلار به 487.1 میلیارد دلار رسیده است.
بدیهی است که اعداد فوق میزان تغییر را مشخص میکنند؛ اما احتمالاً میخواهیم بدانیم که علت این تغییر نیز چه بوده است. بدین ترتیب باید نرخ رشد سالانهای که موجب این تغییر شده است را بفهمیم.
در این حالت ذهن ما بیدرنگ به لگاریتم فکر میکند که از رشد به نرخی که موجب آن شده است به صورت معکوس عمل میکند. یعنی:
علت رشد → لگاریتم تغییر
این ایده نقطه شروع خوبی محسوب میشود، اما باید روی آن کار کنیم. ابتدا باید بدانیم که از چه نوع لگاریتمی باید استفاده کنید. ما به نسبت بین آغاز و پایان یعنی 487.1:109.6 در طی 10 سال علاقهمند هستیم. بدین ترتیب میتوانیم تفکر ابتدایی خود را چنین تکامل ببخشیم:
علت رشد → لگاریتم طبیعی نسبت رشد
بنابراین علت برابر با نرخ 1.492 یا 149.2 درصد بوده است؛ اما کار ما هنوز به پایان نرسیده است. لگاریتمها اهمیتی نمیدهند که یک تغییر چه مقدار طول میکشد که رخ بدهد. آنها صرفاً یک عدد به ما میدهند که اگر این تغییر در یک دوره زمانی مشخصی قرار بود اتفاق بیفتد چه مقدار میبود.
این تغییر میتوانست در واقع در طی یک سال منفرد به میزان رشد پیوسته 149.2 درصد رخ بدهد و یا این که در طی دو سال با نرخ رشد سالانه 74.6 درصد و یا هر ترکیب دیگری اتفاق بیفتد.
در این سناریو میدانیم که تغییر در طی 10 سال رخ داده است و از این رو نرخ آن میبایست به صورت زیر باشد:
از چشمانداز رشد پیوسته آنی، اقتصاد ایران سالانه رشدی برابر با 14.92 درصد داشته است.
نرخ پیوسته از منظر رشدکننده است، طوری که گویی ما نیز همراه با اقتصاد حرکت میکنیم. با این حال یک بانکدار بیشتر به تفاوتهای سال به سال علاقه مند است که برای انسان قابلفهمتر هستند. این موضوع با تداوم رشد به مدت بازههای یکساله قابل دست یافتن است:
تأثیر رشد → توان با نرخ و زمان
رشد =
بدین ترتیب میدانیم که میزان رشد سال به سال برابر با 16.09 درصد بوده است که به دلیل ترکیب، کمی بالاتر از 14.92 درصد کلی است. به بیان دیگر:
با مبنای لحظه به لحظه، یک بخش خاص از اقتصاد به میزان 14.92 درصد رشد میکند که میتوان آن را به صورت بیان کرد.
در مبنای سال به سال با استفاده از تأثیر ترکیب رشد اقتصادی به صورت 16.09 بوده است که به صورت قابل تصور است.
در حوزه مالی ما ممکن است بخواهیم تغییرات سال به سال را داشته باشیم که به خوبی با روندهای دیگر قابل مقایسه است. در علوم و مهندسی ممکن است رفتار مدلسازی در مبنای حرکات آنی مطلوب باشد.
توصیف رشد طبیعی
این جمله را در نظر بگیرید: «فرض کنید باکتریها هر 24 ساعت یک بار دو برابر شوند، فرمول رشد را بیابید»
جمله فوق حالت ابهامبرانگیزی دارد. آیا کولنیهای باکتریها در بازههای زمانی که برای انسان قابل تشخیص است، تکثیر مییابند و آیا ما باید منتظر بمانیم تا آنها دقیقاً دو برابر شوند؟
توصیف بهتر چنین است که «به این کولنی باکتری توجه کنید. ما آن را به مدت یک ساعت تحت نظر گرفتیم و جمعیت آنها از 2.3 گرم به 2.32 گرم افزایش یافت. الان برای ناهار میرویم و محاسبه کنید که وقتی سه ساعت دیگر بازگردیم، جمعیت آنها چقدر شده است؟»
سناریوی فوق را مدلسازی میکنیم. ما به یک لگاریتم برای یافتن نرخ رشد نیاز داریم و سپس از یک توان برای نشان دادن رشد رو به جلو استفاده میکنیم. همانند مثال قبلی همه چیز را در آغاز بر مبنای لگاریتم طبیعی محاسبه میکنیم.
عامل رشد به صورت زیر است:
علت رشد → لگاریتم تغییر
= (رشد)ln
این نرخ رشد یک ساعت است و مدل کلی برای نشان دادن رشد رو به جلو به صورت زیر است:
تأثیر رشد → توان با نرخ و زمان
اگر با 2.32 آغاز کنیم و رشد به مدت 2.32 ساعت ادامه داشته باشد به نتیجه زیر میرسیم:
حال اگر بخواهیم مدت زمان مورد نیاز برای دو برابر شدن باکتری را محاسبه کنیم:
از لحاظ مکانیکی باید لگاریتم طبیعی را از دو سمت حذف کنیم و فرایند به توان رساندن را معکوس نماییم؛ اما میخواهیم معنای شهودی آن را نیز درک کنیم.
اگر 2 نتیجه نهایی باشد، در این صورت (ln(2 ورودی رشدی است که ما را به آنجا میرساند (نرخ × زمان). میدانیم که نرخ برابر با 0.0086 است و از این رو زمان برای رسیدن به رشد دو برابری به صورت زیر است:
= ساعت
جمعیت کولنی پس از حدوداً 80 ساعت دو برابر میشود.
اما این تغییر چشمانداز واقعاً به چه معنی است؟
درک این که آیا ما به ورودی (علت رشد) نیاز داریم یا خروجی (نتیجه رشد) کاملاً سرراست است؛ اما چشمانداز رشد را چگونه میتوان به تصویر کشید.
تصور کنید کارگران کوچکی دارید که مشغول ساخت الگوی رشد نهایی ما هستند (به مقاله توانها مراجعه کنید).
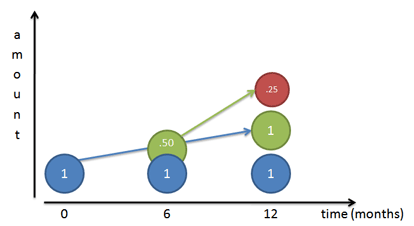
اگر نرخ رشد برابر با 100% باشد، به کارگر اول خود (آقای آبی) میگوییم که به طور مداوم کار کند و در انتهای سال یک کپی از خودش ایجاد کند. اگر کار او را به صورت روز به روز پیگیری کنیم، میبینیم که در انتهای سال، کار ایجاد یک کپی از خودش (آقای سبز) را به پایان برده است.
اما آن کارگری که شروع به ساختش کرده است (آقای سبز) نیز خود مشغول کار میشود. اگر آقای سبز در ماه ششم برای نخستین بار ظاهر شود، فقط نیمی از سال را برای کار کردن زمان دارد و اگر با همان نرخ رشد سالانه آقای آبی کار کند، شروع به ساخت آقای قرمز میکند. البته آقای قرمز نیز شروع به ساخت یک کپی از خودش میکند و این کار نیمهتمام میماند، چون آقای سبز از نیمه سال شروع به کار کرده است.
اگر آقای سبز پس از 4 ماه ظاهر میشود چه رخ میداد؟ یک ماه؟ یک روز؟ یا یک ثانیه؟ اگر کارگرها بیدرنگ شروع به رشد میکردند، ما منحنی رشد لحظه به لحظهای را به دست میآوردیم که به وسیله نمایش مییابد.
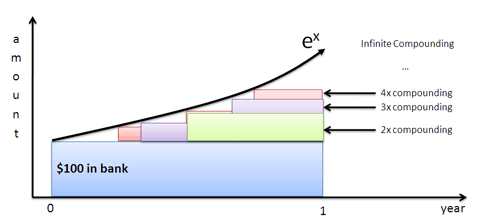
لگاریتم طبیعی نرخ رشد را بر حسب چشمانداز یک کارگر منفرد ارائه میکند. این نسبت را به صورت بیان میکنیم تا بتوانیم نتیجه نهایی را با همه ترکیبهای شاملش ببینیم.
استفاده از مبناهای دیگر
سوئیچ کردن به یک نوع دیگر از لگاریتم (مبنای 10، مبنای 2 و غیره) به این معنی است که به دنبال الگویی برای رشد کلی میگردیم و نه کارگر منفردی که کار میکند. هر الگوریتم مانند یک سؤال است که به دنبال یک تغییر میگردد:
- لگاریتم بر مبنای e: نرخ آنی رشد هر کارگر چه قدر است؟
- لگاریتم بر مبنای 2: چه مقدار دو برابر شدن مورد نیاز است؟
- لگاریتم بر مبنای 10: چه مقدار ده برابر شدن مورد نیاز است؟
برای مثال تصور کنید در طی 30 سال تعداد ترانزیستورهایی که روی یک تراشه الکترونیکی جای میگیرد از 1000 به 1 میلیارد رسیده باشد. در این صورت به سؤال زیر چگونه میتوان پاسخ داد؟
- ریزتراشهها موجودیت منحصر به فردی نیستند که در طی زمان به طور همواری رشد کنند. تراشهها نسخههای مختلفی دارند که شرکتهای متفاوتی تولید میکنند و به طور کلی نمایانگر یک روند عمومی هستند.
- از آنجا که ما با روند توسعه یک میکروچیپ همقدم نمیشویم، پس یک مقیاس ایجاد میکنیم که برای خوانایی انسان مناسب باشد. دو برابر شدن سادهترین تفکر در مورد ده برابر شدن است.
با فرضیات فوق داریم:
علت رشد → لگاریتم تغییر
علت رشد برابر با تقریباً 20 بار دو برابر شدن است که در طی 30 سال رخ میدهد. بدین ترتیب هرساله تقریباً 3/2 دو برابر شدن رخ داده است یا در طی هر 1.5 سال دو برابر شدن اتفاق میافتد. این یک قاعده سرانگشتی مناسب به دست میدهد.
از منظر رشدکننده چنین محاسبه میکنیم:
یعنی 46 درصد رشد پیوسته که دریافت مفهوم آن در این سناریو کمی دشوار است.
تغییر فرمول مبنای لگاریتم
در این بخش به توضیح روش تغییر مبنای لگاریتم میپردازیم. با فرض نرخ رشد 100% پیوسته:
- (Ln(x زمانی که برای رشد به اندازه x نیاز داریم.
- (Ln(2 زمانی که برای رشد به اندازه 2 نیاز داریم.
از آنجا که زمان مورد نیاز برای دو برابر شدن را در اختیار داریم، میتوانیم دریابیم که این زمان چگونه در کل زمان جای میگیرد تا زمان مورد نیاز برای رشد به x را به دست آوریم:
= تعداد دو برابر شدنها از 1 تا x
برای نمونه چه تعداد دو برابر شدن از 1 تا 64 رخ میدهد؟
میدانیم که ln(64) = 4.158. و ln(2) =.693. تعداد دو برابر شدنها به صورت زیر به دست میآید:
در دنیای واقعی، محاسبهگرها ممکن است فاقد دقت کافی باشند؛ از این رو باید از لگاریتم مستقیم در مبنای 2 در صورت امکان استفاده کنیم. در این صورت یک عدد کسری به دست میآوریم. برای رسیدن از 1 به جذر 2 به نیمی از دو برابر شدن نیاز داریم یا به بیان دیگر log2(1.414) = 0.5.
با تغییر دادن مبنای لگاریتم به 10 در واقع به شمارش تعداد ده برابر شدنها برای رسیدن به رشدی خاص میپردازیم:
تعداد ده برابر شدنها از 1 تا x:
سخن پایانی
یادگیری به معنی یافتن توضیحات پنهان در پس مفهومها است. یادگیری یعنی دریابیم یک مفهوم چه زمانی مورد استفاده قرار میگیرد؟ چه نقطهنظری برای این مسئله مورد نیاز است؟ تفسیر کنونی ما این است که توانها از علت در برابر تأثیر سؤال میکنند و از رشدکننده در برابر ناظر رشد صحبت میکنند.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضی و فیزیک
- لگاریتم و هر آنچه باید دربارهش بدانید – معرفی مفاهیم پایه به زبان ساده
- مجموعه آموزشهای ریاضیات
- آموزش ریاضی پایه دانشگاهی
- نماد علمی — به زبان ساده
- توضیح توان در ریاضیات — به زبان ساده
- آموزش ریاضیات عمومی ۱
==












