پشتیبان، اطمینان، بالابری و عقیده – مفاهیم کاربردی در کاوش قواعد وابستگی

در داده‌کاوی و به ویژه کاوش قواعد وابستگی (Association Rule Mining)، به منظور انتخاب قواعد جالب از میان مجموعه‌ای از قواعد ممکن، محدودیت‌های گوناگونی (به عنوان آستانه) بر سنجه‌های مختلف مرتبط با اهمیت و جالبی (interestingness)، اعمال می‌شود. شناخته شده‌ترین محدودیت‌ها در کاوش قواعد وابستگی، آستانه کمینه برای پشتیبان (support) و اطمینان (confidence) هستند. همچنین، معیارهای دیگری از جمله بالابری (Lift) و عقیده (Conviction) نیز در همین راستا مورد استفاده قرار می‌گیرند.

در این مطلب، مفاهیم هر یک از مباحث مذکور تشریح خواهد شد. در کلیه تعاریف فرض می‌شود که X یک مجموعه اقلام، $$X \rightarrow Y$$ یک قاعده وابستگی و T مجموعه‌ای از تراکنش‌های یک پایگاه داده (که به عنوان ورودی مساله داده شده) است. همچنین، به منظور درک بهتر مفاهیم، برای هر یک از آن‌ها مثال‌هایی ارائه خواهد شد.

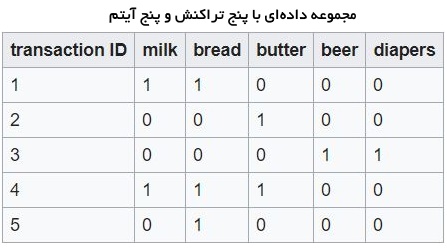
در کلیه این مثال‌ها از مجموعه داده زیر (پایگاه داده تراکنشی) استفاده شده است. این مجموعه داده شامل پنج تراکنش (دارای شماره شناسه تراکنش ۱ الی ۵) و پنج آیتم (شیر، نان، کره، آب جو و پوشک بچه) است. عدد ۱ برای هر آیتم در یک تراکنش، به معنی وجود آن محصول در تراکنش مذکور است. بالعکس، وجود صفر به معنای آن است که آیتم مشخص شده در آن تراکنش خاص وجود ندارد.

پشتیبان (Support)

پشتیبان شاخصی است از اینکه یک مجموعه اقلام (itemset) چند بار در یک مجموعه داده (data set) ظاهر می‌شود. پشتیبان X، با توجه به T، به صورت کسر تراکنش‌های t در مجموعه داده‌ای که شامل مجموعه اقلام X است تعریف می‌شود.

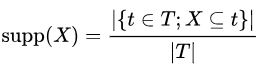
در مجموعه داده معرفی شده در بالا، مجموعه اقلام {X = {beer, diapers دارای پشتیبان ۰.۲ = ۱/۵ است. زیرا در ۲۰٪ تراکنش‌ها به وقوع پیوسته است (یک تراکنش از کل پنج تراکنش). آرگومان ()supp، مجموعه‌ای از پیش شرط‌ها است و بدین ترتیب با رشد کردن محدودکننده‌تر می‌شود (به جای آنکه جامع‌تر شود).

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

اطمینان (Confidence)

اطمینان شاخصی است از اینکه یک قاعده چند بار درست (True) بوده. مقدار اطمینان یک قاعده ($$X \rightarrow Y$$)، با توجه به مجموعه تراکنش T، عبارت است از کسری از تراکنش‌های شامل X که شامل Y نیز هستند. اطمینان به صورت زیر تعریف می‌شود.

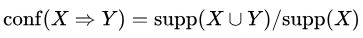
برای مثال، قاعده {butter, bread} $$\rightarrow$$ {milk}، در پایگاه داده، دارای اطمینان ۱ = ۰.۲/۰.۲ است. این یعنی برای ۱۰۰٪ تراکنش‌هایی که شامل کره و نان بوده‌اند این قاعده صحت داشته (۱۰۰٪ دفعاتی که مشتری نان و کره خریده، شیر نیز تهیه کرده است). لازم به ذکر است که $$sup(X \bigcup Y)$$، پشتیبان اتحاد اقلام در X و Y است.

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

مفهوم مطرح شده کمی گیج کننده است زیرا معمولا به طور طبیعی به احتمال رویدادها و نه مجموعه اقلام فکر می‌شود. می‌توان $$sup(X \bigcup Y)$$ را به صورت احتمال $$P(E_X \bigcap E_Y)$$ بازنویسی کرد که در آن $$E_X$$ و $$E_Y$$ رویدادهایی هستند که تراکنش در آن‌ها به ترتیب شامل مجموعه اقلام X و Y است. اطمینان را می‌توان تخمین احتمال شرطی $$P(E_X | E_Y)$$ تفسیر کرد که احتمال یافتن RHS قواعد در تراکنش‌های تحت این شرط وجود دارد، که آن‌ها نیز شامل LHS باشند.

بالابری (Lift)

بالابریِ یک قاعده به صورت زیر تعریف می‌شود.

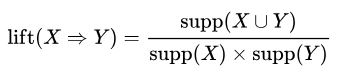
اگر X و Y مستقل باشند، نسبت پشتیبان مشاهده شده مورد نظر است. برای مثال، قاعده {milk, bread} $$\rightarrow$$ {butter} دارای بالابری 1.25 = 0.4 × ۰.۴ / ۰.2 است. اگر قاعده دارای بالابری ۱ باشد، به طور ضمنی دلالت بر این دارد که احتمال پیش‌آمد مقدم و نتیجه از یکدیگر مستقل هستند. هنگامی که دو رویداد مستقل از هم هستند، هیچ قاعده‌ای را نمی‌توان با این دو رویداد ایجاد کرد.

اگر بالابری بزرگ‌تر از یک باشد، به داده‌کاو اجازه می‌دهد که بداند درجه کدام دو پیش‌آمد وابسته به دیگری است و این قواعد را به طور بالقوه برای پیش‌بینی نتیجه در مجموعه داده آینده مورد استفاده قرار می‌دهد. اگر بالابری کمتر از یک باشد، به داده‌کاو اجازه می‌دهد که بداند اقلام جایگزین یکدیگر هستند. این بدین معناست که حضور یک آیتم تاثیر منفی بر حضور آیتم دیگر دارد و بالعکس.

ارزش بالابری از آنجا ناشی می‌شود که هم اطمینان یک قاعده و هم کلیت مجموعه داده را در بر دارد. برای تشریح بیشتر مساله می‌توان گفت، در داده‌کاوی و یادگیری قواعد وابستگی، بالابری سنجه‌ای است که کارایی مدل هدف (قاعده وابستگی) را در پیش‌بینی یا دسته‌بندی اقلام در راستای داشتن یک پاسخ بهبود یافته (با توجه به جمعیت کل)، که در تقابل با یک مدل هدفمند انتخاب تصادفی اندازه‌گیری شده می‌سنجد.

یک مدل هدفمند در صورتی که پاسخ (واکنش) به هدف برای جمعیت کل بهتر از میانگین باشد، عملکرد خوبی خواهد داشت. به بیان ساده، بالابری، نسبت مقادیر پاسخ هدف و میانگین پاسخ در شرایطی است که اولی بر دومی تقسیم شود. به عنوان مثالی دیگر، فرض می‌شود که یک جمعیت نرخ پاسخ میانگین ۵٪ دارد، اما یک مدل (یا قاعده) خاص بخشی با نرخ پاسخ ۲۰٪ را شناسایی کرده است. بنابراین، مقدار lift برابر با ۴.۰ (۵٪/۲۰٪) خواهد بود.

فیلم آموزش مهندسی هستی شناسی در وب معنایی (رایگان) در فرادرس

کلیک کنید

معمولا، مدل‌ساز در تلاش برای تقسیم جمعیت به چندک‌ها و رتبه‌بندی آن‌ها بر اساس بالابری است. سازمان‌ها می‌توانند هر چندک را در نظر بگیرند و با وزن‌دهی به نرخ پاسخ پیش‌بینی شده (و مزایای مالی مربوط به آن) در مقابل هزینه، تصمیم بگیرند که آیا در آن چندک بازاریابی کنند یا خیر. اگر با بالابری به مثابه «دقت» (precision) مواجهه شود که در «بازیابی اطلاعات» (information retrieval) کسر مثبت‌هایی است که مثبت صحیح (True Positive) هستند، می‌توان گفت بالابری مشابه با سنجه «دقت متوسط» (average precision) است.

فیلم آموزش داده کاوی Data Mining در متلب MATLAB در فرادرس

کلیک کنید

منحنی بالابری را می‌توان به عنوان تغییری در منحنی مشخصه عملکرد سیستم (Receiver operating characteristic) محسوب کرد، که در اقتصادسنجی نیز با عنوان منحنی «لورنز» (Lorenz) یا «منحنی توان» (power curve) شناخته شده است. برای مثال دیگری از بالابری، مجموعه داده زیر مفروض است.

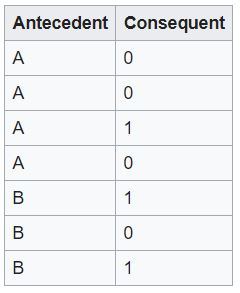
در این مجموعه داده، مقدم متغیر ورودی تحت کنترل داده‌کاو و نتیجه (موخر) متغیری است که داده‌کاو سعی در پیش‌بینی آن دارد. مسائل جهان واقعی داده‌کاوی، مقدم‌های پیچیده‌تری دارند ولی معمولا تمرکز بر نتایج تک مقداری است. اغلب الگوریتم‌های کاوش، قواعد زیر را دنبال می‌کنند (مدل‌های هدفمند).

• قاعده ۱: A دلالت دارد بر ۰
• قاعده ۲: B دلالت دارد بر ۱

زیرا این موارد متداول‌ترین الگوهای یافت شده در داده‌ها هستند. انجام یک بررسی ساده روی جدول بالا، این قواعد را واضح‌تر می‌سازد. پشتیبان برای قاعده ۱ برابر با ۳.۷ است، زیرا این تعداد اقلام موجود در مجموعه داده است که در آن‌ها مقدم A و نتیجه ۰ است. پشتیبان برای قاعده ۲ برابر با ۲.۷ است زیرا دو تا از هفت رکورد به مقدم‌های B و نتایج 1 مربوط هستند. پشتیبان‌ها را می‌توان به صورت زیر نوشت.

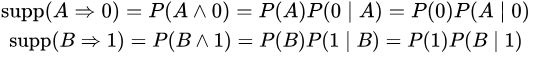
اطمینان برای قاعده ۱ برابر با ۳/۴ است زیرا سه تا از چهار رکورد که مقدم A دارند به نتیجه ۰ می‌رسند. اطمینان برای قاعده ۲ برابر با ۲/۳ است، زیرا دو تا از سه رکوردی که مقدم B دارند، به نتیجه ۱ می‌رسند. اطمینان را می‌توان به صورت زیر نوشت.

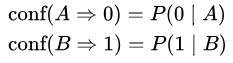
بالابری را می‌توان با تقسیم اطمینان بر احتمال غیر شرطی نتیجه‌ها یا تقسیم پشتیبان بر احتمال مقدم، ضرب در احتمال نتیجه به دست آورد.

بالابری برای قاعده ۱ برابر است با (3/4)/(4/7) = (3*7)/(4 * 4) = 21/16 ≈ 1.31

بالابری برای قاعد ۲ برابر است با (2/3)/(3/7) = (2*7)/(3 * 3) = 14/9 ≈ 1.56

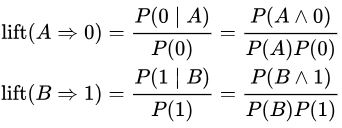
اگر برخی از قواعد دارای بالابری ۱ باشند، به طور ضمنی دلالت بر آن دارند که احتمال وقوع مقدم و احتمال وقوع نتیجه از یکدیگر مستقل است. هنگامی که دو رویداد مستقل از هم هستند، هیچ قاعده‌ای نمی‌تواند در برگیرنده آن دو باشد. اگر بالابری بزرگ‌تر از یک باشد (lift > 1)، مشابه آنچه برای قواعد ۱ و ۲ وجود دارد، این امکان فراهم می‌شود که داده‌کاو بداند درجه کدام دو پیش‌آمد به یکدیگر وابسته است، و این قواعد را برای پیش‌بینی توالی در مجموعه داده‌های آتی کارآمد می‌سازد.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

شایان توجه است که قاعده ۱ دارای اطمینان بالاتری است زیرا بالابری کمتری دارد. به نظر می‌رسد که قاعده ۱ به دلیل داشتن اطمینان بالاتر (صحت بالاتری دارد چون پشتیبانی بهتری نیز دارد)، ارزشمندتر است. اما صحت قاعده مستقل از داده گمراه کننده است. ارزش بالابری (lift) به آن است که دارای اطمینان برای قاعده و به طور کل مجموعه داده باشد.

عقیده (Conviction)

عقیده یک قاعده به صورت زیر تعریف می‌شود.

$$conv(X \rightarrow Y) = 1-supp(Y)/1-conf(X \rightarrow Y)$$

برای مثال، قاعده {milk, bread} $$\rightarrow$$ {butter} دارای عقیده ۱.۲ = 0.5 - 1 / 0.4 - 1 و قابل تفسیر به عنوان تعداد تکرار مورد انتظار وقوع X بدون Y است (در واقع، تعداد تکراری است که قاعده پیش‌بینی اشتباه انجام می‌دهد)، اگر X و Y به طور مستقل تقسیم بر تعداد تکرار پیش‌بینی اشتباه شوند. در این مثال، مقدار عقیده ۱.۲ نشانگر آن است که قاعده {milk, bread} $$\rightarrow$$ {butter} به میزان ۲۰٪ بیشتر مواقع نادرست است (۱.۲ دفعات) اگر ارتباط بین X و Y صرفا شانس تصادفی باشد.

اگر نوشته بالا برای شما مفید بوده، آموزش‌های زیر نیز به شما پیشنهاد می‌شود:

• آمار، احتمالات و داده‌کاوی
• آموزش آزمون آماری و پی مقدار (p-value)
• مدل‌سازی، برازش و تخمین
• شبکه‌های عصبی مصنوعی
• الگوریتم ژنتیک و محاسبات تکاملی
• یادگیری ماشین و بازشناسی الگو

^^