مولفه های تنش روی صفحات مورب – آموزش جامع

در مبحث «تغییر طول عضو‌های تحت بار محوری»، مقاطع عرضی و تنش‌های نرمال موجود بر روی آن‌ها را مورد بررسی قرار دادیم. در این مقاله، به معرفی مؤلفه‌های تنش (تنش نرمال، تنش برشی، تنش‌های اصلی و تنش‌های برشی ماکسیمم) بر روی مقاطع مورب خواهیم پرداخت. در انتها نیز به منظور آشنایی با نحوه به کارگیری روابط ارائه شده برای تحلیل تنش‌های موجود بر روی این مقاطع، چند مثال را تشریح خواهیم کرد.

مقطع عرضی

شکل زیر، یک میله منشوری تحت بارهای محوری P را نمایش می‌دهد. با در نظر گرفتن مقطعی در میانه میله (مانند مقطع mn) می‌توانیم نمودار جسم آزاد بخشی از میله را رسم کنیم.

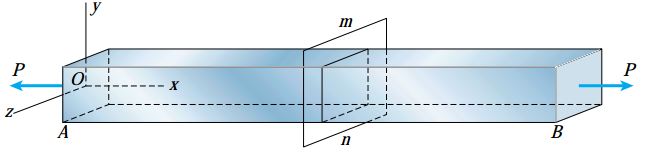
در صورت منشوری بودن میله (یکنواخت بودن سطح مقطع در راستای محور طولی)، همگن بودن مواد تشکیل‌دهنده آن، اعمال بار محوری P بر روی مرکز هندسی سطح مقطع و فاصله کافی مقطع مورد نظر از نواحی تمرکز تنش، توزیع تنش درون میله یکنواخت خواهد بود.

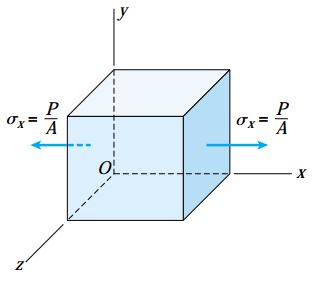
به این ترتیب می‌توان مقدار تنش‌های نرمال اعمال شده بر روی مقطع mn را با استفاده از رابطه σ_x=P/A محاسبه کرد. در شکل زیر، مقطع mn بر محور طولی میله عمود است و به همین دلیل، هیچ تنش برشی بر روی این مقطع وجود ندارد.

برای راحتی بیشتر محاسبات، معمولاً به جای به کارگیری نمای پیچیده سه‌بعدی (شکل بالا) از نمای دوبعدی (شکل زیر) به منظور نمایش وضعیت تنش بر روی مقاطع میله استفاده می‌شود. اگرچه، در هنگام استفاده از نمای دوبعدی باید ضخامت میله در راستای عمود بر صفحه را نیز برای انجام محاسبات در نظر داشته باشید.

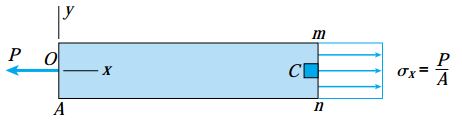
حالت تنش بر روی یک مقطع عرضی

کاربردی‌ترین روش برای نمایش تنش‌های میله نمایش شده در بخش قبلی، جدا کردن یک المان کوچک از ماده (مانند المان C در شکل زیر) و رسم تنش‌های اعمال شده بر روی تمام صفحات آن است.

به این نوع المان، «المان تنش» (Stress Element) گفته می‌شود. المان تنش در نقطه C، یک بلوک کوچک مربعی یا مستطیلی است که صفحه سمت راست آن بر روی مقطع mn قرار دارد.

در تئوری، ابعاد یک المانِ تنش بی‌نهایت کوچک است اما به منظور نمایش واضح‌تر مؤلفه‌های تنش، این المان با مقیاس بزرگ رسم می‌شود (مانند شکل زیر). اضلاع المان نمایش داده شده در شکل زیر با محورهای y ،x و z موازی هستند و تنها تنش‌های نرمال σ_x بر روی صفحه x اعمال می‌شوند.

حالت تنش بر روی صفحات مورب

المان تنش نمایش داده شده در بخش قبلی، تنها نمای محدودی از تنش‌های درون یک میله در شرایط بارگذاری محوری را نمایش می‌دهد.

برای درک بهتر و کامل‌تر حالت تنش، باید مولفه‌های اعمال شده بر روی صفحات مورب را مورد ارزیابی قرار دهیم. به عنوان مثال، مقطع به وجود آمده از صفحه مورب pq در میله زیر را در نظر بگیرید.

با فرض یکسان بودن میزان تنش در تمام نقاط میله، توزیع تنش‌های اعمال شده بر روی مقطع مورب به صورت یکنواخت خواهد بود. نحوه توزیع تنش‌ها بر روی این مقطع، در نمودار جسم آزاد سه‌بعدی و دوبعدی زیر نمایش داده شده است. با در نظر گرفتن شرایط تعادلِ جسمِ آزاد، برآیند تنش‌ها باید برابر با نیروی افقی P باشد (خط‌چین نمایش داده شده در دو شکل زیر).

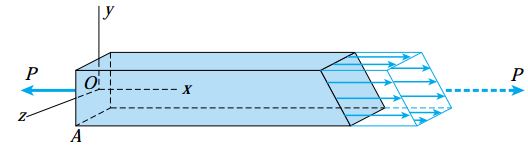
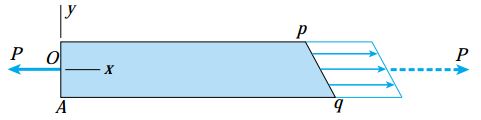
به عنوان یک نکته ابتدایی در نظر داشته باشید که برای مشخص کردن جهت‌گیری مقطع مورب pq باید از یک قاعده کلی استفاده کنیم. معمولاً زاویه θ بین محور x و بردار نرمال n به عنوان جهت‌گیری مقطع مورب در نظر گرفته می‌شود. برای مقطع pq در شکل‌های بالا، زاویه θ حدود 30 درجه است. برای مقطع mn، به دلیل هم‌جهت بودن بردار نرمال و محور x، مقدار زاویه θ صفر بود. برای درک بهتر این موضوع، المان مکعبی بخش قبل را در نظر بگیرید. در این المان، زاویه θ برای صفحه سمت راست 0 درجه، برای صفحه بالایی 90 درجه، برای صفحه سمت چپ 180 درجه و برای صفحه پایینی 270 یا 90- درجه است.

با در نظر گرفتن توضیحات بالا، تنش‌های اعمال شده بر روی مقطع مورب pq را تعیین می‌کنیم. همان طور که قبلاً از نیز اشاره شد، برآیند این تنش‌ها با نیروی P در راستای x برابر است. این نیروی برآیند را می‌توان به دو مؤلفه تجزیه کرد. مؤلفه اول، نیروی نرمال N در راستای عمود بر سطح مقطع pq و مؤلفه دوم، نیروی برشی V در راستای مماس بر این مقطع خواهد بود.

به منظور تعیین مؤلفه‌های حاصل از تجزیه نیروی برآیند P از روابط زیر استفاده می‌کنیم:

تنش‌های نرمال و برشی نیز به ترتیب بر اثر اعمال نیروهای N و V بر روی مقطع مورب ایجاد می‌شوند. توجه داشته باشید که توزیع این تنش‌ها بر روی pq به صورت یکنواخت است.

مقدار تنش نرمال از تقسیم نیروی نرمال N بر مساحت سطح مقطع و مقدار تنش برشی نیز از تقسیم نیروی برشی V بر مساحت سطح مقطع محاسبه می‌شود. بنابراین:

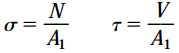
A₁، مساحت سطح مقطع مورب را نمایش می‌دهد و با استفاده از رابطه زیر به دست می‌آید:

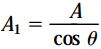
به طور معمول، مساحت سطح مقطع عمود بر محور طولی میله با A نمایش داده می‌شود. با توجه به شکل‌های بالا، جهت اعمال تنش نرمال σ و تنش برشی τ به ترتیب با جهت اعمال نیروی نرمال N و نیروی برشی V یکسان است. به منظور جلوگیری از اشتباهات در محاسبات باید یک قاعده استاندارد برای نام‌گذاری و علامت‌گذاری تنش‌های اعمال شده بر روی مقاطع مورب را مورد استفاده قرار دهیم.

به این ترتیب، برای نمایش تنش‌های اعمال شده بر روی یک مقطع مورب تحت زاویه θ از اندیس θ و برای نمایش تنش‌های اعمال شده بر روی یک مقطع عمود بر محور x از اندیس x استفاده می‌کنیم. علاوه بر این، تنش‌های نرمال σ_θ در شرایط بارگذاری کششی را با علامت مثبت و تنش‌های برشی τ_θ در شرایط دوران پادساعت‌گرد ماده را با علامت منفی نمایش می‌دهیم. به عنوان مثال، تنش‌های نرمال و برشی نمایش داده شده در شکل زیر مثبت هستند.

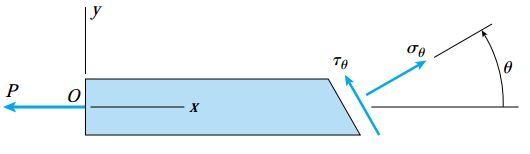
برای یک میله تحت کشش، نیروی نرمال N باعث ایجاد تنش‌های نرمال مثبت و نیروی برشی V باعث ایجاد تنش‌های برشی منفی می‌شود. مقادیر این تنش‌ها با استفاده از معادلات زیر به دست می‌آیند:

رابطه کلی σ_x=P/A برای تعیین تنش نرمال بر روی یک مقطع و همچنین با روابط مثلثاتی زیر را در نظر بگیرید:

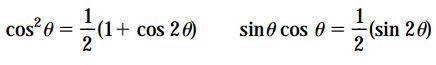
با استفاده از روابط بالا، به معادلات زیر برای تعیین تنش‌های نرمال و برشی دست می‌یابیم:

این معادلات، مقادیر تنش‌های اعمال شده بر روی یک مقطع مورب تحت زاویه θ نسبت به محوری x را تعیین می‌کنند. به عنوان یک نکته مهم در نظر داشته باشید که معادلات بالا تنها با استفاده از روابط استاتیکی به دست آمده‌اند و هیچ ارتباطی با خواص ماده ندارند. از این‌رو، این معادلات برای تمام مواد (خطی یا غیر خطی، الاستیک یا غیر الاستیک) قابل استفاده هستند.

تنش‌های نرمال و برشی ماکسیمم

نحوه تغییرات مقادیر تنش با توجه به تغییر زاویه سطح مقطع مورب در نمودار زیر نمایش داده شده است.

محور افقی این نمودار، زاویه θ در محدوده 90- تا 90 درجه و محور عمودی آن، تنش‌های نرمال و برشی را نمایش می‌دهد. توجه داشته باشید که مقدار مثبت زاویه θ در جهت پادساعت‌گرد اندازه‌گیری می‌شود.

با توجه به نمودار بالا، تنش نرمال σ_θ در زاویه θ=0 با تنش σ_x برابر خواهد شد. با افزایش یا کاهش زاویه θ، مقدار تنش نرمال نیز کاهش می‌یابد و در θ=±90 به مقدار صفر می‌رسد. دلیل این امر، موازی بودن سطح مقطع در نظر گرفته شده با محور طولی المان است. به این ترتیب، تنش نرمال ماکسیمم در زاویه θ=0 رخ می‌دهد:

توجه: مقدار تنش نرمال در زاویه θ=±45 با نصف تنش نرمال ماکسیمم برابر است.

مقدار تنش برشی τ_θ در زوایای θ=0 و همچنین θ=±90 برابر با صفر است. در بین این زوایا، مقدار تنش برشی مطابق نمودار بالا تغییر می‌کند. این تنش در زاویه θ=-45 به مقدار حداکثری مثبت و در زاویه θ=+45 به مقدار حداکثری منفی می‌رسد. تنش‌های برشی ماکسیمم دارای مقادیر برابر هستند. مقدار این تنش‌ها از رابطه زیر به دست می‌آید:

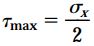
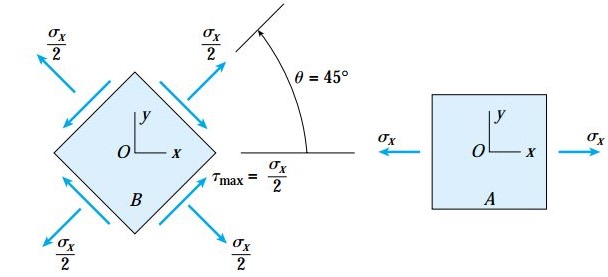
شکل زیر، تنش‌های ماکسیمم در یک میله تحت کشش را نمایش می‌دهد. درون این میله، المان A با زاویه دوران θ=0 و المان B با زاویه دوران θ=45 انتخاب شدند. با توجه به توضیحات و روابط ارائه شده در بخش‌های قبلی، المان A تحت تنش‌های نرمال ماکسیمم و المان B تحت تنش‌های برشی ماکسیمم قرار دارد.

تنها تنش‌های موجود بر روی المان A، تنش‌های نرمال ماکسیمم هستند و هیچ تنش برشی بر روی هیچ‌یک از صفحات این المان وجود ندارد. با این وجود، وضعیت المان B متفاوت است. در این المان، علاوه بر تنش‌های برشی،  تنش‌های نرمال نیز بر روی تمام صفحات اعمال می‌شوند. برای نمونه، صفحه موجود در زاویه 45 درجه (صفحه بالایی در سمت راست المان) را در نظر بگیرید. تنش‌های نرمال برشی موجود بر روی این صفحه به ترتیب با استفاده از روابط σ_x/2 و σ_x/2- به دست می‌آیند. علامت‌های هریک از این روابط با توجه به کششی بودن تنش نرمال (مثبت) و ساعت‌گرد بودن تنش برشی (منفی) انتخاب شده‌اند.

برای محاسبه تنش‌های موجود بر روی صفحات دیگر می‌توان θ=-45 ،θ=135 و θ=-135 را در روابط زیر جایگزین کرد:

با محاسبه مقادیر تنش‌های موجود بر روی صفحات دیگر درمی‌یابیم که اگر المانی تحت زاویه 45 درجه نسبت به محور اعمال بار دوران یافته باشد، تنش‌های نرمال بر روی تمام صفحات المان دوبعدی برابر با σ_x/2 و تمام تنش‌های برشی نیز برابر با σ_x/2 خواهند بود. علاوه بر این، به خاطر داشته باشید که تنش‌های اعمال شده بر روی دو صفحه عمود بر هم دارای مقادیر برابر هستند و جهت‌گیری آن‌ها به گونه‌ای است که به هم نزدیک یا از هم دور می‌شوند. در مبحث «تنش و کرنش برشی» و «تنش و کرنش نرمال»، این دو نوع تنش را به طور کامل مورد ارزیابی قرار داده‌ایم.

اگر میله‌ای تحت فشار قرار داشته باشد، تنش σ_x فشاری و مقدار آن منفی در نظر گرفته می‌شود. به این ترتیب، جهت‌گیری تمام تنش‌های اعمال شده بر روی المان تنش برعکس شرایط بارگذاری کششی خواهد بود. اگرچه، تمام روابط ارائه شده برای محاسبات در شرایط فشاری نیز برای این حالت قابل استفاده هستند و تنها باید تنش σ_x را به عنوان یک کمیت منفی در نظر گرفت. می‌دانیم که مقدار تنش برشی ماکسیمم در یک میله تحت بار محوری برابر با نصف تنش نرمال ماکسیمم است.

با این وجود، اگر مقاومت ماده در حین اعمال برش نسبت به مقاومت آن در حین اعمال کشش کمتر باشد، امکان ایجاد شکست بر اثر تنش‌های برشی وجود خواهد داشت. نمونه‌ای از این نوع شکست در شکل زیر نمایش داده شده است. در این شکل، یک بلوک چوبی در شرایط بارگذاری فشاری قرار دارد و تحت زاویه 45 درجه نسبت به راستای اعمال فشار می‌شکند.

 

رخ دادن شکست برشی در راستای یک صفحه 45 درجه‌ای در یک بلوک چوبی تحت فشار

در فولاد نرم (فولاد سازه‌ای) تحت کشش نیز رفتاری مشابه با شکل بالا رخ می‌دهد. در حین انجام آزمایش کششی بر روی یک میله تخت صیقلی از جنس فولاد کم‌کربن، نوارهای لغزشی بر روی سطوح میله با زاویه حدود 45 درجه ایجاد می‌شوند (شکل زیر). این نوارها نشان می‌دهند که نمونه آزمایشگاهی زیر در راستای صفحات دربرگیرنده تنش برشی ماکسیمم در حال برش است. این پدیده برای اولین بار توسط «گیوم پایوبرت» (Guillaume Piobert) در سال 1942 و سپس توسط «دابلیو لودرز» (W. Lüders) در سال 1860 مشاهده شد. به همین دلیل، نوارهای لغزشی با عنوان نوارهای لودرز یا پایوبرت نیز شناخته می‌شوند. این نوارها در لحظه رسیدن ماده به تنش تسلیم رخ می‌دهند.

نوارهای لغزشی در نمونه‌ای از یک میله فولادی صیقلی تحت بارگذاری کششی

تنش تک‌محوری

حالتی از تنش که در این مقاله مورد بررسی قرار گرفت، با عنوان «تنش تک‌محوری» (Uniaxial Stress) شناخته می‌شود. دلیل این نام‌گذاری، قرارگیری ماده تحت کشش یا فشار ساده در یک جهت است. θ=0 و θ=45 به عنوان مهم‌ترین زوایای المان تنش در حالت تنش تک‌محوری به شمار می‌روند؛ چراکه تنش نرمال ماکسیمم در زاویه 0 درجه و تنش برشی ماکسیمم در زاویه 45 درجه رخ می‌دهد.

اگر زاویه مقطع مورد بررسی با این دو زاویه تفاوت داشته باشد، مقادیر تنش‌های اعمال شده بر روی صفحات المان‌های دوران یافته، با استفاده از روابط زیر قابل محاسبه خواهند بود:

توجه: تنش تک‌محوری، یکی از حالت‌های خاص «تنش صفحه‌ای» (Plane Stress) محسوب می‌شود.

مثال‌ها

به منظور آشنایی بیشتر با مفهوم تنش‌های موجود بر روی صفحات مورب و نحوه استفاده از روابط ارائه شده در این مقاله، به تشریح دو مثال می‌پردازیم.

مثال 1

شکل زیر، یک میله منشوری با مساحت سطح مقطع A=1200mm² را نمایش می‌دهد که تحت فشار بار محوری P=90kN قرار رفته است. با توجه به اطلاعات مسئله، مقادیر مربوط کمیت‌های زیر را محاسبه کنید:

• الف) تنش‌های اعمال شده بر روی مقطع مورب pq در زاویه θ=25
• ب) حالت کلی تنش برای θ=25

الف) تنش‌های موجود بر روی مقطع مورب

به منظور تعیین تنش‌های اعمال شده بر روی یک مقطع مورب در زاویه θ=25، ابتدا تنش نرمال σ_x را محاسبه می‌کنیم:

علامت منفی در رابطه بالا، بیانگر فشاری بودن تنش است. در مرحله بعد، تنش‌های نرمال و برشی در زاویه θ=25 را تعیین می‌کنیم:

این مقادیر، تنش‌های اعمال شد بر روی مقطع دوران مورب در شکل زیر را نمایش می‌دهند. توجه داشته باشید که تنش نرمال σ_θ دارای علامت منفی (فشاری) و تنش برشی τ_θ دارای علامت مثبت (پادساعت‌گرد) است.

ب) حالت کلی تنش

به منظور تعیین حالت کلی تنش باید مقادیر تنش‌های اعمال شده بر روی تمام صفحات المان دوران یافته تحت زاویه 25 درجه را محاسبه کنیم. صفحه ab دارای زاویه θ=25 است. بنابراین، جهت‌گیری آن با مقطع مورب در بخش قبلی سؤال مطابقت دارد. در نتیجه، مقادیر تنش‌های موجود بر روی ab برابر با مقادیر به دست آمده در بخش الف خواهند بود. مقادیر تنش‌های موجود بر روی صفحه cd نیز با مقادیر تنش‌های موجود بر روی صفحه ab برابر هستند. برای اطمینان از این موضوع می‌توانید θ=25+180 را درون معادلات مربوطه جایگذاری کنید. به منظور تعیین مقادیر تنش‌های موجود بر روی صفحه ad نیز مقدار θ=25-90 را درون روابط تنش‌های نرمال و برشی قرار می‌دهیم:

مقادیر تنش‌های موجود بر روی صفحه bc با مقادیر بالا برابر هستند. برای اطمینان از این موضوع می‌توانید روابط مربوطه را با θ=25+90 حل کنید. توجه داشته باشید که تنش نرمال در این مسئله به صورت فشاری است و تنش برشی به صورت پادساعت‌گرد اعمال می‌شود. شکل زیر، حالت کلی تنش برای بخش ب این مثال را نمایش می‌دهد. رسم این شکل، روش بسیار خوبی برای نمایش جهت‌گیری تنش‌ها و راستای صفحات دربرگیرنده آن‌ها است.

مثال 2

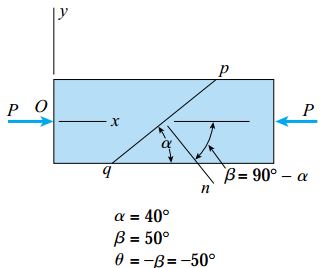
شکل زیر، یک میله تحت فشار با مقطع مربعی و ابعاد b را نمایش می‌دهد که باید بار P=1800lb را تحمل کند. این میله از دو بخش تشکیل شده است که توسط یک اتصال چسبی در کنار یکدیگر قرار گرفته‌اند. سطح اتصال این دو بخش (صفحه pq) به اندازه α=40 نسبت به راستای عمود زاویه دارد. میله مورد بررسی از جنس یک پلاستیک سازه‌ای با تنش فشاری مجاز 1100psi و تنش برشی مجاز 600psi است. به علاوه، تنش‌های فشاری و برشی مجاز در سطح اتصال نیز به ترتیب 750psi و 500psi هستند. با توجه به اطلاعات مسئله، حداقل ابعاد میله را تعیین کنید.

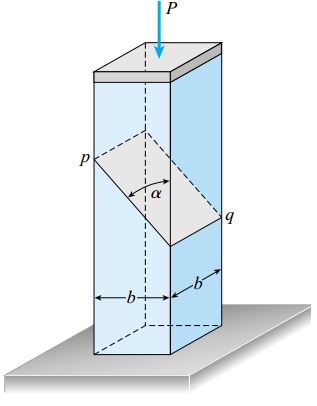
برای راحتی کار، میله را به صورت افقی در نظر می‌گیریم (مشابه میله مورد بررسی در متن مقاله). در این حالت، اختلاف زاویه بردار نرمال صفحه pq نسبت به محور میله برابر با β=90-α=50 خواهد بود. به دلیل مثبت بودن زاویه θ در اندازه‌گیری پادساعت‌گرد، زاویه اتصال چسبی برابر با θ=-50 می‌شود.

رابطه بین مساحت سطح مقطع میله با بار P و تنش σ_x به صورت زیر تعریف می‌شود:

با توجه به مشخص بودن بار P، برای یافتن مساحت مورد نیاز باید مقدار σ_x را تعیین کنیم. بنابراین، با مشخص کردن کمترین مقدار σ_x، مساحت مورد نیاز به دست می‌آید. برای محاسبه مقادیر σ_x می‌توانیم از روابط ارائه شده برای σ_θ و τ_θ زیر استفاده کنیم:

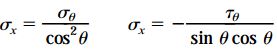
اکنون این روابط را برای پلاستیک و اتصال چسبی مورد استفاده قرار می‌دهیم.

الف) تعیین مقادیر σx بر اساس تنش‌های مجاز اتصال چسبی

برای شرایط فشار بر روی اتصال چسبی، مقادیر σ_θ=-750psi و θ=-50 را داریم. با جایگذاری این مقادیر در روابط مربوطه، خواهیم داشت:

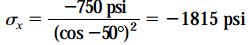
برای شرایط برش در اتصال چسبی، تنش مجاز برابر با 500psi است. با این وجود نمی‌توان فوراً در مورد مثبت یا منفی بودن τ_θ اظهار نظر کرد. برای تشخیص این موضوع دو رویکرد وجود دارد. در رویکرد اول، مقادیر مثبت و منفی τ_θ در رابطه σ_x جایگذاری می‌شوند. در این حالت، یک مقدار منفی و یک مقدار مثبت برای σ_x به دست می‌آید. اگر تنش اعمال شده بر روی ماده فشاری باشد، مقدار منفی σ_x و اگر کششی باشد، مقدار مثبت σ_x را انتخاب می‌کنیم. در رویکرد دوم، از جهت‌گیری بارهای اعمال شده و ساعت‌گرد/پادساعت‌گرد بودن تنش برشی نسبت به سطح مقطع مورد بررسی کمک می‌گیریم. در این مثال، تنش برشی به صورت ساعت‌گرد بر روی اتصال چسبی اعمال می‌شود. بنابراین، با در نظر گرفتن τ_θ=-500psi و θ=-50 خواهیم داشت:

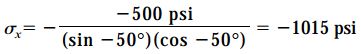
ب) تعیین مقادیر σx بر اساس تنش‌های مجاز پلاستیک

تنش فشاری ماکسیمم در پلاستیک بر روی سطح مقطع عمود بر راستای محور طولی میله رخ می‌دهد. به این ترتیب، با در نظر گرفتن مقدار 1100psi برای تنش فشاری مجاز، خواهیم داشت:

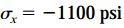
تنش برشی ماکسیمم بر روی صفحه‌ای با زاویه 45 درجه رخ می‌دهد. مقدار این تنش برابر با σ_x/2 است. در نتیجه، با در نظر گرفتن مقدار 600psi برای تنش برشی مجاز، خواهیم داشت:

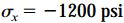
با جایگذاری τ_θ=600 و θ=45 در رابطه زیر نیز مقدار بالا به دست می‌آید.

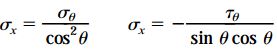
ج) تعیین حداقل ابعاد میله

با مقایسه مقادیر به دست آمده برای σ_x در بخش الف و ب مشاهده می‌کنیم که σ_x=-1015psi دارای مقدار کوچک‌تری است. بنابراین، طراحی باید بر اساس این مقدار صورت گیرد. با جایگذاری σ_x در رابطه مساحت سطح مقطع، خواهیم داشت:

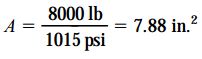
به دلیل مربعی بودن سطح مقطع میله، رابطه مساحت آن با A=b² برابر است. به این ترتیب، حداقل عرض مجاز برای میله برابر با مقدار زیر خواهد بود:

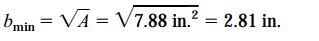
اگر عرض میله بیشتر از b_min باشد، تنش‌های به وجود آمده در این مسئله از مقادیر مجاز عبور نخواهند کرد.

^^