رگرسیون خطی ساده – مفهوم و محاسبات به زبان ساده
در این مطلب از مجله فرادرس در مورد رگرسیون خطی ساده و محاسبات آن صحبت میکنیم. استفاده از دادهها به منظور کشف رابطه بین آنها اساس دادهکاوی است. یکی از ابزار سنجش رابطه و مدلسازی استفاده از ابزار آماری رگرسیون است. امروزه به منظور تحلیل و کشف مدل روی «مه داده» (کلانداده | Big Data)، روشهای مختلف رگرسیون توسعه یافته است. استفاده از تحلیل رگرسیون خطی ساده در علوم مختلف دادهکاوی، بخصوص مبحث «آموزش ماشین» (Machine Learning)، فیزیک، شیمی و علوم زیستی کاربرد بسیاری دارد.


مفهوم رگرسیون خطی ساده
در آمار، رگرسیون خطی یک رویکرد مدل خطی بین متغیر «پاسخ» (Response) با یک یا چند متغیر «توصیفی» (Explanatory) است. اغلب برای کشف مدل رابطهی خطی بین متغیرها از رگرسیون (Regression) استفاده میشود. در این حالت فرض بر این است که یک یا چند متغیر توصیفی که مقدار آنها مستقل از بقیه متغیرها یا تحت کنترل محقق است، میتواند در پیشبینی متغیر پاسخ که مقدارش وابسته به متغیرهای توصیفی و تحت کنترل محقق نیست، موثر باشد. هدف از انجام تحلیل رگرسیون شناسایی مدل خطی این رابطه است.
در ادامه از متغیر وابسته به جای متغیر پاسخ و متغیر مستقل به جای متغیر توصیفی استفاده میکنیم.

از آنجایی که ممکن است علاوه بر متغیرهای مستقل، عوامل زیاد و ناشناخته دیگری نیز در تعیین مقدار متغیر وابسته نقش داشته باشند، مدل رگرسیونی را با مناسبترین تعداد متغیر مستقل در نظر گرفته و میزان خطا را به عنوان نماینده عوامل تصادفی دیگری که قابل شناسایی نبودند در نظر میگیریم که انتظار است کمتر در تغییرات متغیر وابسته نقش داشته باشند.
ضریب همبستگی
برای سنجش شدت رابطه بین متغیر وابسته و مستقل میتوان از ضریب همبستگی استفاده کرد. هر چه ضریب همبستگی به ۱ یا ۱- نزدیکتر باشد، شدت رابطه خطی بین متغیرهای مستقل و وابسته شدیدتر است. البته اگر ضریب همبستگی نزدیک به ۱ باشد جهت تغییرات هر دو متغیر یکسان است که به آن رابطه مستقیم میگوییم و اگر ضریب همبستگی به ۱- نزدیک باشد، جهت تغییرات متغیرها معکوس یکدیگر خواهد بود و به آن رابطه عکس میگوییم. ولی در هر دو حالت امکان پیشبینی مقدار متغیر وابسته برحسب متغیر مستقل وجود دارد.
هرچند ضریب همبستگی راهی برای نشان دادن رابطه بین دو متغیر مستقل و وابسته است ولی مدل رابطه بین این دو متغیر را نشان نمیدهد. با رگرسیون میتوان قانونی که بین دادهها وجود دارد را کشف و به کار بست. بسیاری از رابطههای فیزیک یا شیمی به کمک رگرسیون بدست آمده است. برای مثال مقدار ثابت گازها در فیزیک کلاسیک از طریق رگرسیون قابل محاسبه است.
نمایش رابطهی خطی بین دو متغیر مستقل و وابسته معمولا توسط «نمودار نقطهای» (Scatter Plot) انجام میشود. برای آشنایی با شیوه ترسیم نمودار نقطهای میتوانید به مطلب نمایش و رسم نمودار برای دادهها — معرفی و کاربردها مراجعه کنید.
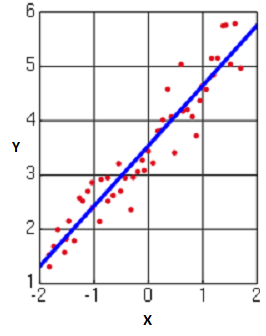
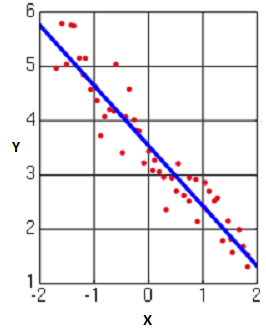
با توجه به تصویر بالا مشخص است که محور افقی مقدارهای متغیر مستقل و محور عمودی مقدارهای متغیر وابسته را نشان میدهد و رابطهی بین دو متغیر مستقیم است. ولی در تصویر زیر رابطه شدید ولی در جهت عکس بین دو متغیر مستقل و وابسته دیده میشود.
تاریخچه رگرسیون
واژه رگرسیون برای اولین بار در مقاله معروف «فرانسیس گالتون» (Sir Francis Galton) دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال ۱۸۷۷ اشاره میکند که قد فرزندان قد بلند به میانگین قد جامعه میل میکند. او این رابطه را «بازگشت» (Regress) نامید.
هر چند واژه رگرسیون در شاخه علوم زیستی معرفی شد ولی آنچه امروزه به نام رگرسیون میشناسیم، روشی است که توسط «گاوس» (Gauss) در سال ۱۸۰۹ معرفی شد تا به کمک آن پارامترهای مجهول رابطه بین مدار سیارههای منظومه شمسی را برآورد کند.
بعدها روش گاوس توسط «پیرسون» (Pearson) توسعه یافت و با مفاهیم آماری آمیخته شد. همچنین پیرسون توزیع توام متغیر وابسته و مستقل را توزیع گاوسی در نظر گرفت. بعدها «فیشر» (R. A. Fisher) توزیع متغیر وابسته به شرط متغیر مستقل را توزیع گاوسی محسوب کرد.
مدل رگرسیون خطی ساده
اگر برای شناسایی و پیشبینی متغیر وابسته فقط از یک متغیر مستقل استفاده شود، مدل را «رگرسیون خطی ساده» (Simple Linear Regression) میگویند. فرم مدل رگرسیون خطی ساده به صورت زیر است:
همانطور که دیده میشود این رابطه، معادله یک خط است که جمله خطا یا همان به آن اضافه شده. پارامترهای این مدل خطی عرض از مبدا () و شیب خط () است. شیب خط در حالت رگرسیون خطی ساده، نشان میدهد که میزان حساسیت متغیر وابسته به متغیر مستقل چقدر است. به این معنی که با افزایش یک واحد به مقدار متغیر مستقل چه میزان متغیر وابسته تغییر خواهد کرد. عرض از مبدا نیز بیانگر مقداری از متغیر وابسته است که به ازاء مقدار متغیر مستقل برابر با صفر محاسبه میشود. به شکل دیگر میتوان مقدار ثابت یا عرض از مبدا را مقدار متوسط متغیر وابسته به ازاء حذف متغیر مستقل در نظر گرفت.
برای مثال فرض کنید کارخانهای میخواهد میزان هزینههایش را براساس ساعت کار برآورد کند. شیب خط حاصل از برآورد نشان میدهد به ازای یک ساعت افزایش ساعت کاری چه میزان بر هزینههایش افزوده خواهد شد. از طرفی عرض از مبدا خط رگرسیون نیز هزینه ثابت کارخانه حتی زمانی که ساعت کاری نیست نشان میدهد. این هزینه را میتوان هزینههای ثابت مانند دستمزد نگهبانان و هزینه روشنایی فضای کارخانه فرض کرد.
گاهی مدل رگرسیونی را بدون عرض از مبدا در نظر میگیرند و محسوب میکنند. این کار به این معنی است که با صفر شدن مقدار متغیر مستقل، مقدار متغیر وابسته نیز باید صفر در نظر گرفته شود. زمانی که محقق مطمئن باشد که که خط رگرسیون باید از مبدا مختصات عبور کند، این گونه مدل در نظر گرفته میشود. فرم مدل رگرسیونی در این حالت به صورت زیر است:
از آنجایی که پیشبینی رابطه بین متغیر وابسته و مستقل به شکل دقیق نیست، جمله خطا را یک «متغیر تصادفی» (Random Variable) با میانگین صفر در نظر میگیرند تا این رابطه دارای اریبی نباشد.

باید توجه داشت که منظور از رابطه خطی در مدل رگرسیون، وجود رابطه خطی بین ضرایب است نه بین متغیرهای مستقل. برای مثال این مدل را نیز میتوان مدل خطی در نظر گرفت در حالیکه مدل دیگر خطی نیست و به مدل نمایی شهرت دارد.
همچنین در فرضیات این مدل، خطا یک جمله تصادفی است و تغییرات آن مستقل از متغیر X است. به این ترتیب مقدار خطا وابسته به مقدار متغیر مستقل نیست.
در رگرسیون خطی سعی میشود، به کمک معادله خطی که توسط روش رگرسیون معرفی میشود، برآورد مقدار متغیر وابسته به ازای مقدارهای مختلف متغیر مستقل توسط خط رگرسیون بدست آید. به منظور برآورد پارامترهای مناسب برای مدل، کوشش میشود براساس دادههای موجود، مدلی انتخاب میشود که کمترین خطا را داشته باشد.
روشهای مختلفی برای تعریف خطا و حداقل کردن آن وجود دارد. معیاری که در مدل رگرسیون خطی ساده به کار میرود، کمینه کردن مجموع مربعات خطا است. از آنجایی که میانگین مقدارهای خطا صفر در نظر گرفته شده است، میدانیم زمانی مجموع مربعات خطا، حداقل ممکن را خواهد داشت که توزیع دادهها نرمال (Normal Distribution) باشند. در نتیجه، نرمال بودن دادههای متغیر وابسته یا باقیماندهها یکی از فرضیات مهم برای مدل رگرسیونی خطی ساده است.
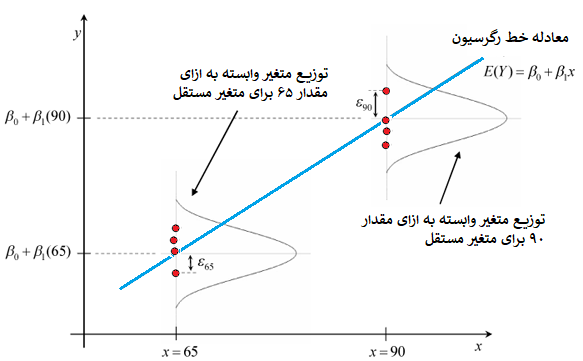
شکل زیر به منظور توضیح نرمال بودن مقدار خطا ترسیم شده است. در هر مقدار از متغیر مستقل ممکن است بیش از یک مقدار برای متغیر وابسته مشاهده شود. مقدار پیشبینی شده برای هر یک از این مقدارها ثابت است که توسط معادله خط رگرسیون برآورد میشود.
برای مثال تعدادی مقدار برای متغیر وابسته براساس مقدار x=65 وجود دارد که شکل توزیع فراوانی آنها به صورت نرمال با میانگین است. همچنین برای نقطه ۹۰ نیز مقدار پیشبینی یا برآورد برای متغیر وابسته به صورت خواهد بود. در هر دو حالت واریانس خطا یا واریانس مقدارهای پیشبینیشده (پهنای منحنی زنگی شکل) ثابت است.
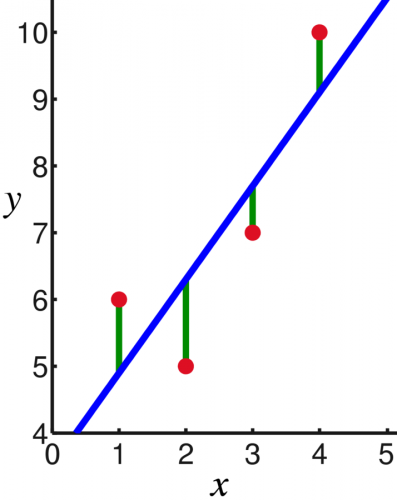
در تصویر زیر چهار نقطه از مشاهدات (x,y) به همراه خط رگرسیون دیده میشوند که در آن خط رگرسیون با رنگ آبی، نقطههای مربوط به مشاهدات با رنگ قرمز و فاصله هر نقطه از خط رگرسیون (خطای برآورد) با رنگ سبز نشان داده شده است.
برای برآورد کردن پارامترهای مدل رگرسیونی باید معادله خطی یافت شود که از بین همه خطوط دیگر دارای کمترین مجموع توان دوم خطا باشد. یعنی برای آن از بقیه خطوط کمتر باشد.
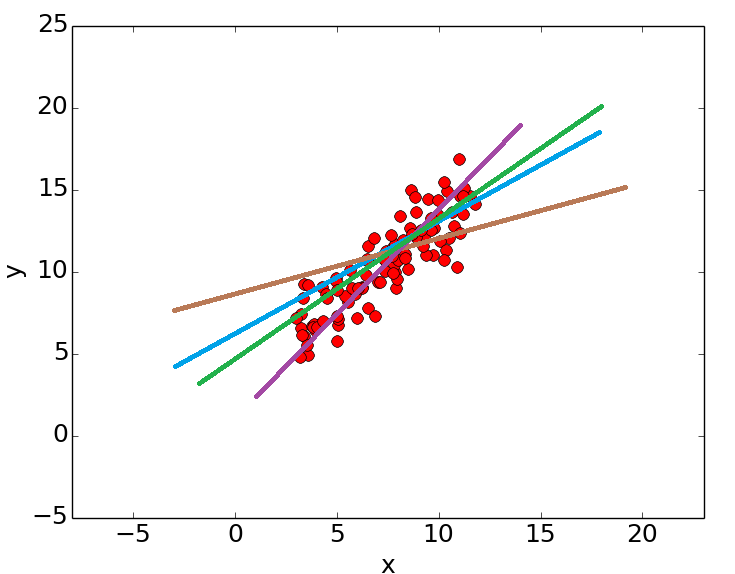
به نظر شما در تصویر بالا، کدام خط دارای مجموع مربعات خطای کمتری است؟ امکان تشخیص بهترین خط بدون استفاده از ابزارهای محاسباتی امکانپذیر نیست. تا اینجا میدانیم رگرسیون خطی چیست. برای آشنایی بیشتر با مفهوم رگرسیون و انواع آن میتوانید به مجموعه آموزش تخمین و رگرسیون مقدماتی تا پیشرفته فرادرس مراجعه کنید.
برآورد پارامترهای رگرسیون خطی ساده
به منظور برآورد پارامترهای رگرسیون خطی ساده، کافی است تابع مجموع مربعات خطا را کمینه کرد. برای این کار مراحل زیر باید طی شوند:
- محاسبه مجموع توان دوم خطا
- مشتق مجموع مربعات خطا برحسب پارامتر
- برابر قرار دادن مشتق با صفر به منظور پیدا کردن نقاط کمینه
- پیدا کردن ریشه برای معادله حاصل برحسب
- مشتق مجموع مربعات خطا بر حسب پارامتر
- جایگذاری و پیدا کردن ریشه برای معادله حاصل برحسب
به این ترتیب برآورد پارامترهای مدل خطی به صورت زیر خواهند بود.
که در آن و میانگین و هستند.
برای راحتی محاسبات، میتوان برآورد را به فرم دیگری نیز نوشت:
که منظور از میانگین حاصلضرب x و y بوده و نیز بیانگر واریانس مقدارهای x است.
اگر مقدار برآورد برای متغیر وابسته باشد، میتوانیم آن را میانگین مشاهدات برای متغیر وابسته به ازای مقدار ثابت متغیر مستقل در نظر گرفت. پس با فرض اینکه میانگین جمله خطا نیز صفر است، خواهیم داشت:
که در آن نشاندهنده امید ریاضی (متوسط) شرطی است و همچنین و برآوردهای مربوط به هر یک از پارامترها هستند.

نکته: به راحتی دیده میشود که میانگین مربوط به متغیر مستقل و وابسته روی خط رگرسیون قرار دارند. یعنی این نقطه در معادله خط رگرسیون صدق میکند. زیرا با توجه به محاسبه داریم:
مثال
اطلاعات مربوط به ۵۰ خانه شامل قیمت (به میلیون ریال) و متراژ (متر مربع) در شهر تهران جمعآوری شده است. این اطلاعات را میتوانید با قالب اکسل از اینجا دریافت کنید.
با توجه به ضریب همبستگی بین این دو متغیر که برابر با 0.9891 است، مشخص است که رابطه خطی شدیدی بینشان برقرار است. اگر فرض کنیم قیمت خانه متغیری وابسته به متراژ است، محاسبات اولیه برای برآورد پارامترهای مدل رگرسیونی در جدول زیر قرار گرفته.
| 84.9 | 451.136 | 40350.6 | 411.724 |
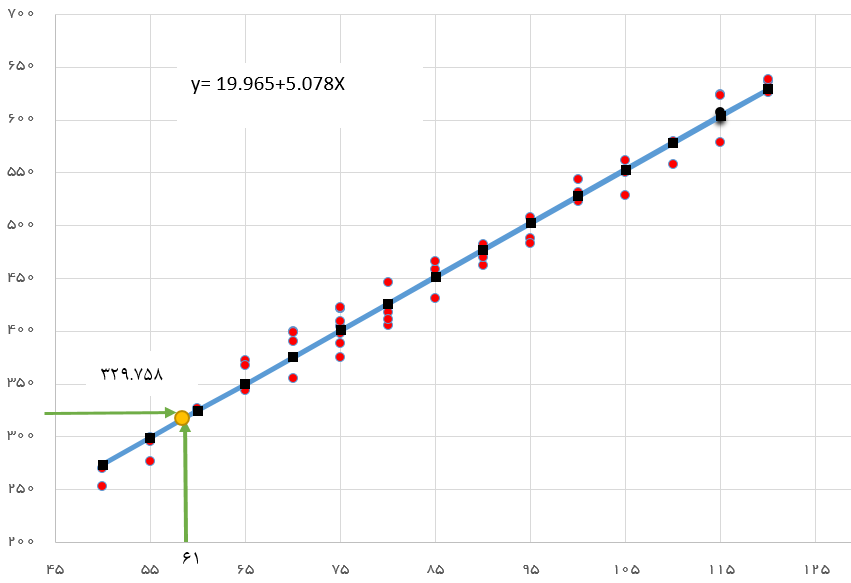
بر این اساس برآورد پارامترهای مدل خطی به صورت و خواهد بود. در نتیجه میتوان معادله مربوط برآورد مقدار متغیر وابسته را به صورت زیر نوشت:
پس اگر لازم باشد که ارزش خانهای با متراژ 61 متر محاسبه شود، کافی است در معادله بالا برای مقدار 61 را جایگزین کرده، مقدار را بدست آوریم که برابر با 329.758 میلیون ریال است. در تصویر زیر نمودار مربوط به دادهها و خط رگرسیون دیده میشود.
آزمون مربوط به مدل و پارامترهای آن
بعد از انجام مراحل رگرسیون، با استفاده از جدول «تحلیل واریانس» (Analysis of Variance) میتوان صحت مدل ایجاد شده و کارایی آن را سنجید. اساس کار در تحلیل واریانس، تجزیه واریانس متغیر وابسته به دو بخش است، بخشی از تغییرات یا پراکندگی که توسط مدل رگرسیونی قابل نمایش است و بخشی که توسط جمله خطا تعیین میشود. پس میتوان رابطه زیر را بر این اساس نوشت.
که هر کدام به صورت زیر تعریف شدهاند:
مقدار SST را میتوان مجموع مربعات تفاضل مشاهدات متغیر وابسته با میانگینشان در نظر گرفت که در حقیقت صورت کسر واریانس متغیر وابسته است. این کمیت میتواند به دو بخش زیر تفکیک شود.
شایان ذکر است به مقدار SSE مجموع مربعات خطا نیز گفته میشود که در مدل رگرسیون با توجه به کمینه کردن آن پارامترهای مدل بدست آمد. همچنین بخش بعدی با SSR نشان داده میشود:
که میتواند به عنوان مجموع مربعات تفاضل مقدارهای پیشبینیشده از میانگینشان نامگذاری شود.
در صورتی که مدل رگرسیون مناسب باشد، انتظار داریم سهم SSR از SST زیاد باشد، بطوری که بیشتر تغییرات متغیر وابسته توسط مدل رگرسیون توصیف شود. برای محاسبه واریانس از روی هر یک از مجموع مربعات کافی است حاصل را بر تعداد اعضایشان تقسیم کنیم. به این ترتیب مقدارهای جدیدی به نام «میانگین مربعات خطا» (MSE)، «میانگین مربعات رگرسیون» (MSR) بوجود میآیند. به جدول زیر که به جدول تحلیل واریانس معروف است، توجه کنید.
| منشاء تغییرات | درجه آزادی | مجموع مربعات | میانگین مربعات | آماره F |
| رگرسیون | k-۱ | SSR | ||
| خطا | n-k | SSE | ||
| کل | n-1 | SST |
درجه آزادی برای رگرسیون که با k-۱ نشان داده شده است، یکی کمتر از تعداد پارامترهای مدل (k) است که در رگرسیون خطی ساده برابر با ۱-۲=۱ خواهد بود زیرا پارامترهای مدل در این حالت و هستند. تعداد مشاهدات نیز با n نشان داده شده است.
اگر محاسبات مربوط به جدول تحلیل واریانس را برای مثال ذکر شده، انجام دهیم نتیجه مطابق جدول زیر خواهد بود.
| منشاء تغییرات | درجه آزادی | مجموع مربعات | میانگین مربعات | آماره F |
| رگرسیون | 1 | 520338.1755 | 520338.1755 | |
| خطا | 48 | 11515.7187 | 239.91 | |
| کل | 49 | 531853.8942 |
از آنجایی که نسبت میانگین مربعات دارای توزیع آماری F است با مراجعه به جدول این توزیع متوجه میشویم که مقدار محاسبه شده برای F بزرگتر از مقدار جدول توزیع F با و درجه آزادی است، پس مدل رگرسیون توانسته است بیشتر تغییرات متغیر وابسته را در خود جای دهد در نتیجه مدل مناسبی توسط روش رگرسیونی ارائه شده.
گاهی از «ضریب تعیین» (Coefficient of Determination) برای نمایش درصدی از تغییرات که توسط مدل رگرسیونی بیان شده، استفاده میشود. ضریب تعیین را با علامت نشان میدهند. هر چه ضریب تعیین بزرگتر باشد، نشاندهنده موفقیت مدل در پیشبینی متغیر وابسته است. در رگرسیون خطی ساده مربع ضریب همبستگی خطی همان ضریب تعیین خواهد بود.
در مثال قبل ضریب تعیین برای مدل رگرسیونی برابر با 0.9783 است. بنابراین به نظر میرسد که مدل رگرسیونی در پیشبینی ارزش خانه برحسب متراژ موفق عمل کرده.
نکاتی در مورد رگرسیون خطی ساده
قبل از اتمام کار با مدل رگرسیون نکاتی باید در نظر گرفته شوند. با توجه به تعریف فیشر برای رگرسیون، جمله خطا باید یک متغیر تصادفی با توزیع نرمال باشد. از آنجایی که در انجام محاسبات این فرضیه چک نشده است، باید بعد از محاسبات مربوط به مدل رگرسیون خطی، مقدارهای خطا محاسبه شده و تصادفی بودن و وجود توزیع نرمال برای آنها چک شود.
تصادفی بودن باقیماندهها در رگرسیون خطی ساده
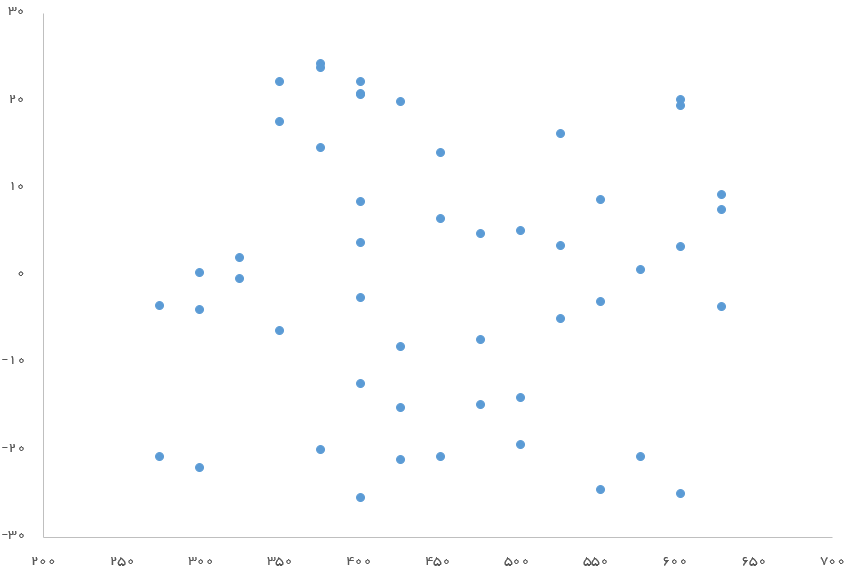
یک راه ساده، برای چک کردن تصادفی بودن مقدارهای خطا میتواند رسم آنها و مقدار پیشبینی شده روی یک نمودار باشد، بطوری که مقدارهای پیشبینی در محور افقی و مقدارهای خطا در محور عمودی ظاهر شوند. اگر در این نمودار، الگوی خاصی مشاهده نشود میتوان رای به تصادفی بودن باقیمانده داد. منظور از الگوی غیرتصادفی، افزایش یا کاهش مقدار خطا با افزایش یا کاهش مقدارهای پیشبینی شده است.
در تصویر زیر این نمودار برای مثال قبلی ترسیم شده است. محور افقی در این نمودار مقدار قیمت خانه و محور عمودی نیز باقیماندهها است. همانطور که دیده میشود، الگوی خاصی وجود ندارد.
نرمال بودن باقیماندهها در رگرسیون خطی ساده
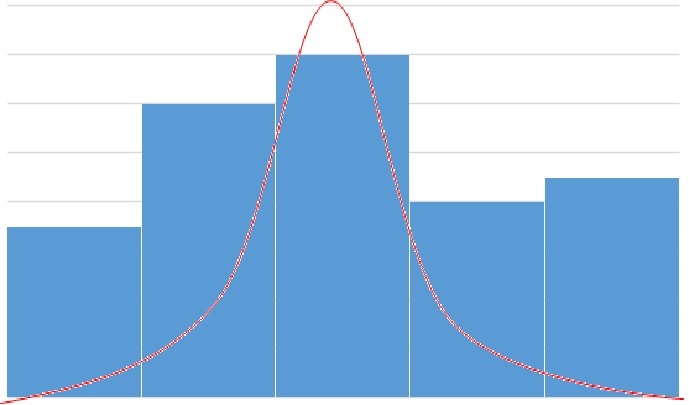
به منظور سنجش نرمال بودن باقیماندهها، ترسیم بافتنگار (نمودار فراوانی -Histogram) میتواند سادهترین راه باشد. در تصویر زیر بافتنگار مربوط به باقیماندههای مثال قبل ترسیم شده است. شکل بدست آمده شبیه توزیع نرمال است و به صورت زنگی شکل درآمده.
البته روش دقیقتر، ترسیم نمودار «چندک-چندک» (Q-Q Plot) برای باقیماندهها یا مشاهدات y و دادههای توزیع نرمال است. در زیر نمودار چندک-چندک برای دادههای مربوط به مثال قبل ترسیم شده است.
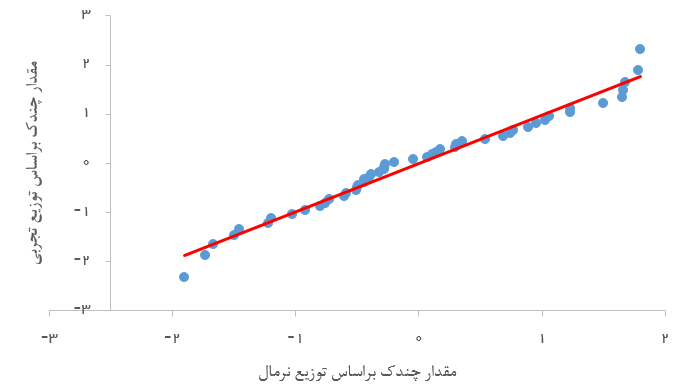
انتظار داریم در این نمودار، اگر دادههای مربوط به متغیر وابسته دارای توزیع نرمال باشند، صدکهای مربوط به آن با صدکهای تولید شده از توزیع نرمال تقریبا یکسان باشند. اگر این اتفاق بیافتد باید نقاط روی نمودار که نشاندهنده زوج صدکهای تولید شده هستند، روی یک خط راست قرار گیرند. این کار را با مقدارهای خطا نیز میتوان انجام داد زیرا متغیر وابسته با مقدارهای خطا رابطه خطی دارد. به این منظور چندکهای توزیع نرمال را با چندکهای توزیع تجربی باقیماندهها مقایسه میکنیم. انتظار داریم که نمودار، نشان دهنده یک رابطه مستقیم خطی باشد. در نتیجه میتوان فرض کرد که باقیماندهها دارای توزیع نرمال هستند.
ثابت بودن واریانس در رگرسیون خطی ساده
از طرفی واریانس جمله خطا نیز طبق فرضیههای اولیه برای مدل رگرسیونی، باید ثابت و برابر با باشد. برآورد واریانس برای جملههای خطا نیز به صورت زیر است:
مشخص است که مقدار بیانگر مقدار مشاهده شده و مقدار پیشبینی برای مشاهده iام است. از آنجایی که در برآورد واریانس احتیاج به دو پارامتر مدل رگرسیونی است، دو درجه آزادی از تعداد مشاهدات کم شده است و در مخرج کسر n-2 قرار گرفته است.
برای آنکه نشان دهیم واریانس نیز ثابت است از نمودار نقطهای استفاده میکنیم که در محور افقی مقدارهای پیشبینیشده و در محور عمودی نیز مقدار باقیماندهها قرار دارد. این نمودار نباید به صورت الگوی افزایشی یا کاهشی باشد. قبلا از این نمودار به منظور چک کردن تصادفی بودن باقیماندهها بهره بردیم.
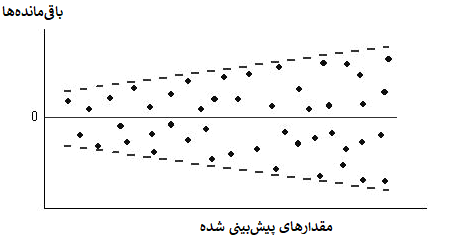
تصویر زیر حالتی را نشان میدهد که واریانس باقیماندهها نسبت به مقدار پیشبینی حالت افزایشی دارد و ثابت نیست.
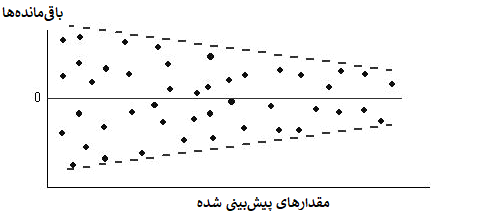
همچنین کاهشی بودن واریانس باقیماندهها نسبت به مقدار پیشبینی در تصویر زیر دیده میشود.
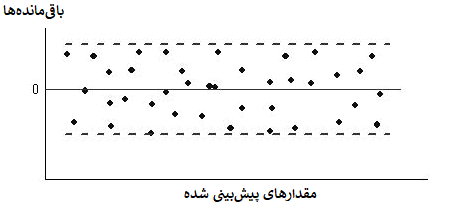
اگر در مدل رگرسیونی باقیماندهها نسبت به مقدار پیشبینی به طور تصادفی حول نقطه صفر تغییر کند، ثابت بودن واریانس قابل شناسایی است. این حالت در تصویر زیر دیده میشود.
آزمون رگرسیون خطی
۱. در مدل رگرسیون خطی ساده، نقش و تعریف متغیر مستقل و متغیر وابسته چیست؟
متغیر مستقل عاملی است که مقدارش تعیین میشود و متغیر وابسته مقداری است که مدل تلاش میکند آن را پیشبینی کند.
متغیر وابسته همان داده ورودی مدل است و متغیر مستقل نتیجه پیشبینیشده توسط مدل خواهد بود.
متغیر مستقل و متغیر وابسته هر دو متغیرهایی هستند که مدل بر اساس آنها ضریب همبستگی را محاسبه میکند بدون تفاوت مشخص.
متغیر مستقل مقدار تصادفی میگیرد ولی متغیر وابسته همواره ثابت باقی میماند.
در مدل رگرسیون خطی ساده، متغیر مستقل، مقداری است که در اختیار داریم یا انتخاب میکنیم تا تاثیرش بر متغیر وابسته سنجیده شود. متغیر وابسته همان مقداری است که مدل تلاش دارد آن را با استفاده از مقدار متغیر مستقل پیشبینی کند.
۲. کدام مورد درست است درباره نقش ضریب همبستگی و تفاوت آن با مدلسازی رگرسیون خطی ساده؟
مدل رگرسیون خطی شدت و جهت رابطه را مشخص میکند اما پیشبینی انجام نمیدهد.
ضریب همبستگی فقط شدت رابطه خطی را میسنجد و جهت رابطه را نشان نمیدهد.
ضریب همبستگی هم جهت و هم شدت رابطه خطی را نشان میدهد اما رابطه را مدلسازی نمیکند.
مدل رگرسیون خطی فقط برای دادههای بدون ارتباط کاربرد دارد و همبستگی بررسی نمیشود.
«ضریب همبستگی هم جهت و هم شدت رابطه خطی را نشان میدهد اما رابطه را مدلسازی نمیکند» درست است زیرا ضریب همبستگی عددی است که قدرت و جهت (مثبت یا منفی بودن) رابطه خطی بین دو متغیر را توصیف میکند، اما فرمول مشخصی برای مدل رابطه ارائه نمیدهد. در مقابل، رگرسیون خطی ساده فراتر از سنجش همبستگی است و یک مدل (معادله ریاضی) برای رابطه تعریف میکند که میتوان با آن پیشبینی انجام داد.
۳. در مدل رگرسیون خطی ساده، جمله خطا چه نقشی دارد و چه فرضهایی در مورد آن مطرح است؟
جمله خطا تنها زمانی در مدل قرار میگیرد که متغیر مستقل عددی نباشد.
جمله خطا فقط برای سادهسازی محاسبات به مدل افزوده میشود.
وجود جمله خطا صرفا نشان میدهد بین متغیرها هیچ رابطهای وجود ندارد.
epsilon بیانگر عوامل تصادفی است و معمولا فرض میشود میانگینش صفر و توزیعش نرمال باشد.
جمله خطا بیانگر سهم عوامل تصادفی یا ناشناخته تاثیرگذار بر متغیر وابسته است و نشاندهنده بخش غیر قابل توضیح توسط مدل خطی میباشد. معمولا فرض میشود میانگین آن صفر است و از توزیع نرمال پیروی میکند تا شرایط بهینه برای برآورد پارامترها فراهم شود.
۴. معادله استاندارد مدل رگرسیون خطی ساده و معنای پارامترهای آن چیست؟
و اثر متغیر تصادفی و میزان خطا را نشان میدهد.
و شیب خط و عرض از مبدا را نشان میدهند.
و و ثابت تصادفی مدل است.
و و به ترتیب میانگین و واریانس دادهها هستند.
فرم صحیح معادله رگرسیون خطی ساده به صورت است. در این مدل، مقدار شیب خط (تاثیر واحدی X بر Y) و عرض از مبدا مدل (مقدار Y وقتی X صفر است) را نشان میدهد.
۵. در کدام حالت حذف کردن عرض از مبدا در مدل رگرسیون خطی ساده قابل قبول است و این حذف چه برداشتی درباره رابطه بین متغیرهای مدل نشان میدهد؟
هرگاه ضریب همبستگی کاملا مثبت باشد.
در شرایطی که شیب خط برابر با صفر باشد.
هنگامی که میانگین خطاها برابر با صفر نباشد.
وقتی اگر متغیر مستقل صفر باشد، انتظار داریم متغیر وابسته هم صفر شود.
حذف عرض از مبدا زمانی مجاز است که فرض کنیم اگر مقدار متغیر مستقل صفر باشد، مقدار متغیر وابسته نیز صفر خواهد بود؛ یعنی نقطه شروع خط از مبدا مختصات است. این فرضیه بیانگر این است که رابطه خطی بدون جابجایی در محور Y برقرار بوده و هیچ مقدار پایهای مستقل از متغیر توضیحی وجود ندارد. بیان فرضهایی مثل غیر صفر بودن میانگین خطاها، صفر بودن شیب یا مثبت بودن ضریب همبستگی، ارتباطی با حذف عرض از مبدا ندارند.
۶. اگر نمودار پراکندگی بین دادههای باقیمانده و مقدار پیشبینیشده هیچ الگوی خاصی نشان ندهد، چه میتوان درباره خطاها نتیجه گرفت؟
ارتباط غیرخطی بین متغیرها وجود دارد.
خطاها به طور تصادفی توزیع شدهاند.
واریانس خطاها ثابت نیست.
خطاها نرمال توزیع نشدهاند.
زمانی که نمودار پراکندگی بین باقیماندهها و مقادیر پیشبینیشده الگویی مشخص یا ساختاری نداشته باشد و دادهها به طور پراکنده و بدون روند خاص دیده شوند، نتیجه این است که خطاها به صورت تصادفی توزیع شدهاند. این ویژگی یکی از فرضهای کلیدی مدل رگرسیون خطی ساده است و تایید میکند که باقیماندهها وابستگی ساختاری ندارند. وجود الگو یا ساختار میتواند نشانه مشکل مانند غیرتصادفی بودن باشد، ولی مشاهده «عدم وجود الگو» نشاندهنده تصادفی بودن است.
۷. در تحلیل واریانس مدل رگرسیون خطی ساده، کدام بخش مجموع مربعات بیانگر پراکندگی توضیحدادهشده توسط مدل است و این مقدار با چه آمارهای برای سنجش معناداری مدل بررسی میشود؟
SSR مجموع مربعات مدل با مقایسه F سنجیده میشود.
SST مجموع مربعات کل با آزمون z سنجیده میشود.
SSR مجموع مربعات مدل با محاسبه R^2 سنجیده میشود.
SSE مجموع مربعات خطا با آماره t سنجیده میشود.
در تحلیل واریانس مدل رگرسیون، مجموع مربعات SSR نشاندهنده آن بخشی از پراکندگی است که مدل رگرسیون آن را توضیح میدهد. برای سنجش معناداری مدل، مقدار SSR را با مجموع مربعات خطا (SSE) مقایسه میکنند و نسبت این دو با آماره F در جدول ANOVA بررسی میشود.
۸. ضریب تعیین در مدل رگرسیون خطی ساده نشاندهنده چیست و مقدار بالای آن چه معنایی دارد؟
نسبت پراکندگی دادهها به خطاهای مدل را میسنجد.
درصد تغییرات متغیر وابسته که مدل توضیح داده را بیان میکند.
فقط میزان همبستگی متغیرها را اندازه میگیرد.
درصد دادههایی که دقیقا روی خط قرار دارند را نشان میدهد.
«ضریب تعیین نشاندهنده درصد تغییرات متغیر وابسته است که مدل رگرسیون خطی توانسته آن را با متغیر مستقل توضیح دهد. مقدار بالای به این معناست که مدل بیشتر تغییرات متغیر وابسته را پیشبینی یا توضیح داده است.













بسیار عالی بود
سپاسگزارم
در این قسمت: جایگذاری \widehat\beta_0 و پیدا کردن ریشه برای معادله حاصل برحسب \widehat{\beta}_1
باید معالده رو با معکوسسازی ماتریس حل کنیم؟ ینی این معاله رو باید حل کرد خلاصه… مهمینجوری با فاکتورگیری اون خط بعدش بدست نمیاد که؟ من یکم گیج شدم/:
با عرض سلام
12 متغییر (نقشه) مستقل دارم برای یه مدل میخام کار کنم با چه روشی , نرم افزار کار کنم عدم وجود چند خطی بین این متغیرها نشان دهند؟ با تشکر
سلام و تشکر برای تحلیل از نمودار y (مقدار مشاهده شده) و خطا استفاده نمی کنیم؟
سلام بر چه اساسي ما تشخيص ميديم كه ما چندتا بايد مدل رگرسيوني براي تجزيه و تحليل داده ها با استفاده از نرم افزار ايويز بنويسيم.؟
ممنون حداقل و حداکثر رگرسیون چند متغیره چه میزان هستش؟متشکرم
سلام. برای پیش بینی متغیر ملاک از روی جنسیت از چه روش اماری استفاده میشه؟
سلام استاد گرامی بسیار ممنون از بابت مطالب مفیدتون.لطفا بفرمایید در بازار ارزهای دیجیتال به چه شکل می توان از مبحث رگرسیون در پیش بینی روند تغییرات استفاده کرد. یا بعبارتی برای کاربران این حوزه چه مباحثی می تواند در زمنیه پیش بینی روند تغییرات کمک موثر و جدی بکند. از اینکه توجه می فرمایید صمیمانه سپاسگزارم. ارادتمند،علیرضا
سلام، وقت شما بخیر؛
از آنجایی که در پیشبینی روند تغییرات، مولفه زمان دخیل است، سریهای زمانی و مدلهای آن برای آینده نگری قیمت ارزهای دیجیتال موثرتر از رگرسیون خطی است. به نظر من بهتر است مطالب سری زمانی در علم داده — از صفر تا صد را مطالعه کنید تا با جنبههای مختلف آن بیشتر آشنا شوید.
سربلند و سرافراز باشید.
با سلام
در مقاله ای برای فراوانی های ۲ ، ۴ ، ۱ ، ۱۱ ، ۱۲
میانگین ۳/۹ و انحراف معیار ۱/۲۷ بدست آمده لطفا در صورت امکان راهنمایی بفرمایید میانگین و انحراف معیار چطور بدست آمده است
سلام و درود به شما دوست گرامی؛
براساس فراوانی ها نمیتوان میانگین و انحراف معیار را مشخص کرد. باید علاوه بر فراوانی، مقادیر نیز موجود باشند. برای مشاهده نحوه محاسبه میانگین و انحراف معیار براساس جدول فراوانی، به نوشتارهای میانگین وزنی — به زبان ساده و واریانس و اندازههای پراکندگی — به زبان ساده را مطالعه کنید.
همواره تندرست و پیروز باشید.
اره خطا باید صفر بشه بنابراین تخمین ما باید با میانگین مطابقت داشته باشه برعکس گفتند
چگونه میتوان ۳ متغیر را به عنوان متغیر مستقل وارد و یک متغیر وابسته در کدوم قسمت ممنون و تفسیر SEدر رگرسبون چی هست ممنون
سلام و عرض ادب
آیا قرار گیری باقی مانده در باند مثبت یا منفی معنای خاصی می دهد؟ آیا محل قرار گیری آنها را بایستی با نمودار زنگوله تطبیق داد؟
سلام دوست و همیار مجله فرادرس،
همانطور که در در نوشتار خواندید، اساس کار آن است که مجموع مربعات جملات خطا (یا باقیمانده) کمینه شود. از طرفی طبق پیشفرضهای مدل رگرسیونی، میانگین یا امید ریاضی متغیر تصادفی خطا (باقیمانده) صفر است. که البته این موضوع در اکثر مواقع براساس دادهها نیز تایید میشود. پس میتوان نتیجه گرفت که باقی مانده ها در یک بازه شامل مقدار صفر قرار میگیرند. به این ترتیب اگر باقی مانده در باند مثبت یا منفی باشد، نشانگر مشکل خطای بیشبرآورد یا کمبرآورد برای مقدار متغیر وابسته خواهد بود. اگر میزان باقیمانده مثبت باشد، مقدار واقعی بزرگتر از مقدار پیشبینی است و مشکل کمبرآوردی رخ داده است. در حالت عکس نیز مشکل بیشبرآوردی واضح است. اگر نمودار فراوانی باقیماندهها (توزیع احتمال) زنگی شکل و مطابق با توزیع نرمال باشد، واریانس ثابت بوده و میانگین باید برابر با صفر برای این توزیع باشد. در غیر اینصورت فرضیات اولیه برای مدلسازی رگرسیونی برقرار نیست.
در این صورت یا با تغییر متغیر، عملیات را انجام میدهیم یا از روشهای دیگری غیر از OLS برای اجرای رگرسیون بهره میبریم.
از اینکه همراه مجله فرادرس هستید بسیار سپاسگزاریم.
شاد و تندرست و پیروز باشید.
عالی
دوستان یه منبع انگلیسی که رگرسیون رو مفصل توضیح داده باشه معرفی کنید ممنون میشم
سلام دوست و همراه عزیز مجله فرادرس
احتمالا با مطالعه نوشتارهای مجله فرادرس متوجه شدهاید که روشهای رگرسیونی بسیار متنوع هستند. روشهای پارامتری و غیر پارامتری، روشهای مبتنی برای کمترین مربعات خطا یا کمترین زاویه و … همگی گسترده بوده و در یک کتاب نمی گنجند. ولی به نظر من برای درک بهتر تحلیلهای آماری در مباحث مربوط به یادگیری ماشین بهترین کتاب (+) و (+) هستند.
از مطالعه آنها لذت ببرید.
تندرست، پیروز و شاد باشید.
سلام خط رگرسیون رو کی بلده چند تا سوال دارم نمیتونم حلش کنم
xبار 84.9 هستش و y بار 451.136 پس چجوری XY میشه 40350.6؟
عالی
من متن رو خوندم خیلی عالی بود قشنگ فهمیدم چیه ممنون
صداش خیلی رو مخ بود
بسیار عالی
perfect.Great
درود و سپاس از اموزش خوبتون. اما در مقایسه با کتاب Jeffry Wooldridge انگار SSE و SSR جابجاست.
در کتاب ازمون صحت رگرسیون را با این فرمول گفته ست
SSR=∑(yi−y^i)2
و خطا رو با
SSE=∑(y^i−y¯)2
سلام
ایا میشه بین رگرسیون و خطاهای نوع اول و دوم ، ارتباطی پیدا کرد و اون رو توضیح داد ؟
سلام دوستان عزیز
کسی میتونه لطفا راهنمایی کنه؟
یک محصول 6 متری داریم که در هر متر 1 میلیمتر انحراف از خط راست داره . انحراف در 6 متر چقدر صحیح است؟
در صورتیکه خردش کنیم در هر 1 متر 1 میلیمتر انحراف داره اما در طول 6 متر الان حدود 15 سانتیمتر انحراف داره. میشه روش محاسبه رو بفرمایید.
thanks ,bravo! that was really helpful for me
سلام
واقعا عالی بود، خیلی خیلی ممنون
خلاصه و خیلی مفید بود
بازم ممنون
یه اشکال تایپی داشت تو جدول که جای MSE و MSR اشتباه نوشته شده
سلام و تشکر از توجه شما به مطالب فرادرس
مشکل تایپی حل شده و اصلاح در جدول تحلیل واریانس صورت گرفت… از اینکه همراه فرادرس هستید بسیار سپاسگزاریم.
من معمولاً نظر نمیذارم. اما این دفعه حیفم اومد نظری ندم.
میخواستم بگم :
آفرین به نویسنده این مقاله ، آفرین به سایت فرادرس