توابع زوج و فرد – به زبان ساده
در ریاضیات توابع زوج و فرد به توابعی گفته میشود که نسبت به محور y یا مبدا متقارن باشد. این نامگذاری به این دلیل است که اگر n در تابع f(x)=xn زوج باشد، تابع f زوج و در صورت فرد بودن n، تابع f فرد خواهد بود.

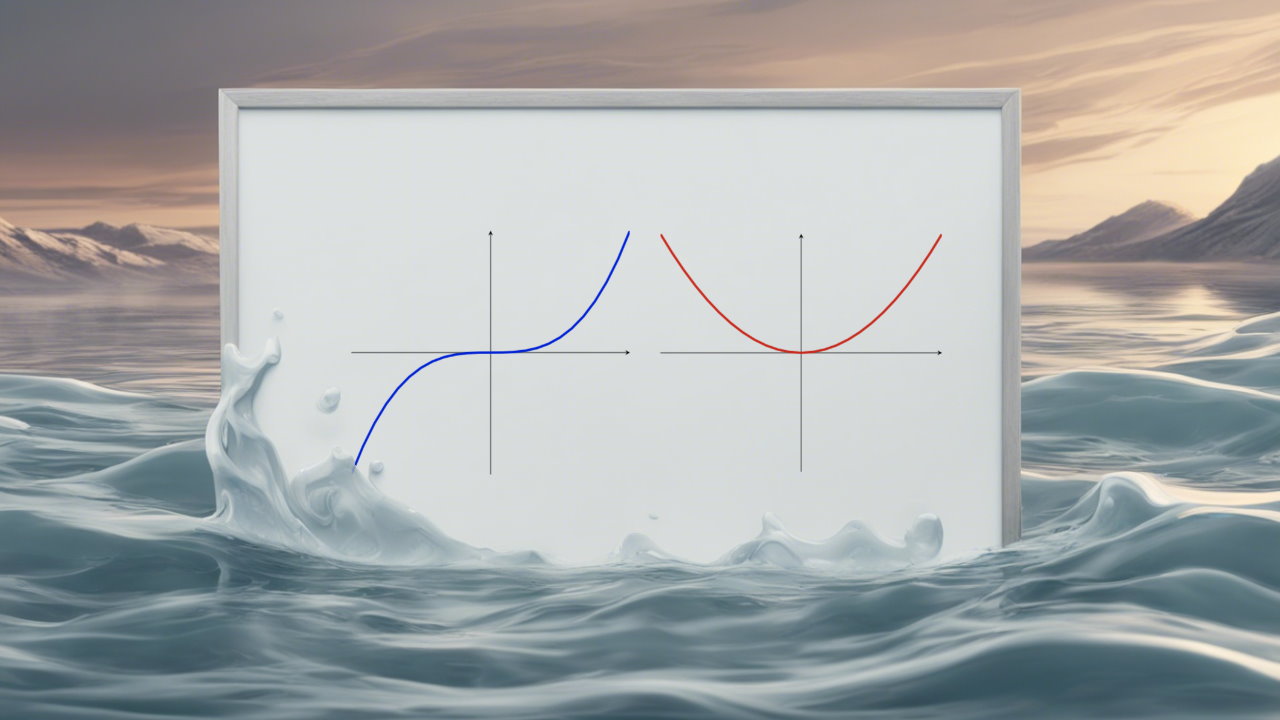
توابع زوج
فرض کنید با تابع (f(x مواجه هستیم. زمانی به این تابع، زوج گفته میشود که رابطه زیر در آن برقرار باشد.
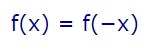
رابطه بالا بیان میکند که تابع زوج نسبت به محور y متقارن است. نمودار ارائه شده در شکل زیر نمونهای از یک تابع زوج را نشان میدهد.
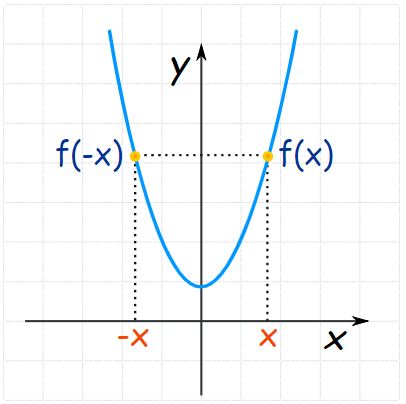
نمودار بالا تابع زیر را نشان میدهد.
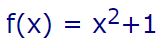
بدیهی است که توابعی همچون x2 ،x4 ،x6 ،x8 زوج هستند. توان تمامی این توابع زوج هستند؛ به همین دلیل به چنین توابعی زوج گفته میشود. توابع دیگری نیز وجود دارند که رفتار آنها زوج است. برای نمونه شکل زیر نمودار تابع (Cos (x را نشان میدهد.
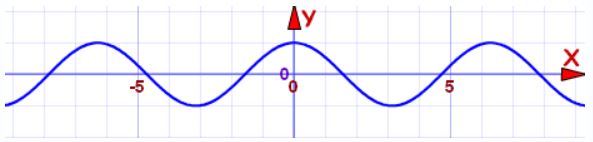
البته دقت داشته باشید که همواره توان زوج، منجر به تابع زوج نخواهد شد. برای نمونه تابع x+1)2)، تابعی زوج محسوب نمیشود.
توابع فرد
به تابعی فرد گفته میشود که رابطه زیر در آن برقرار باشد.
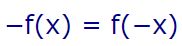
برای درک بهتر توابع زوج و فرد میتوانید فیلم آموزشی رایگان زیر را مشاهده کنید.
در رابطه بالا به علامت منفی پشت پرانتز توجه داشته باشید. این علامت همان عاملی است که نشان دهنده فرد بودن تابع است. رابطه بالا بیان میکند که یک تابع فرد نسبت به مبدا مختصات متقارن است. برای نمونه تابع f(x)=x3-x را در نظر بگیرید. با محاسبه تابع (f(-x متوجه میشویم که این تابع فرد است. در حقیقت:
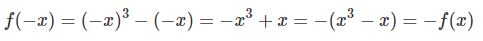
بنابراین رابطه (f(-x)=-f(x برقرار بوده و تابع مذکور فرد است. البته با استفاده از نمودار این تابع نیز میتوان فهید که (f(x فرد است.
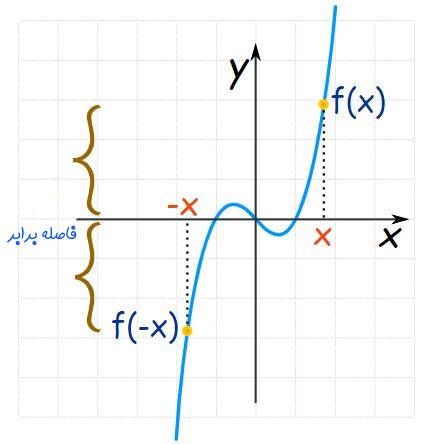
با رسم نمودار یا محاسبه تابع (f(-x، میتوان فهمید که توابع x ،x3 ،x5 ،x7 فرد است. به همین دلیل به چنین توابعی فرد گفته میشود. البته توابع دیگری نیز هستند که فرد محسوب میشوند. برای نمونه تابع (sin (x که در شکل زیر رسم شده نیز فرد است.
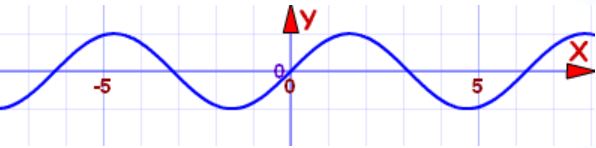
البته توجه داشته باشید که همواره توان فرد منجر به شکلگیری تابع فرد نخواهد شد.
توابع غیرفرد و غیرزوج
بایستی بدانید که فرد و زوج عباراتی هستند که دستهای خاص از توابع را نشان میدهند. در حقیقت اینطور نیست که یک تابع حتما زوج یا فرد باشد. به بیانی صحیحتر اکثر توابع، نه فرد و نه زوج هستند. برای نمونه تابع f(x)=x3-x+1 را در نظر بگیرید. شکل چنین تابعی در نمودار زیر ارائه شده است.
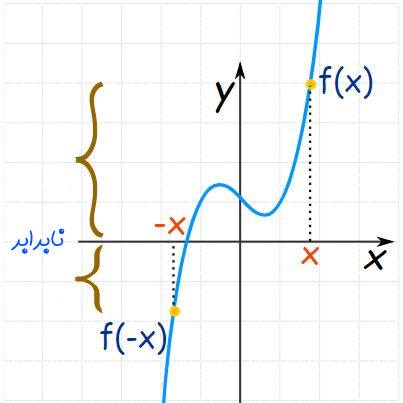
با توجه به این نمودار، تابع f نسبت مرکز مختصات و نسبت به محور y متقارن نیست. از این رو این تابع نه زوج و نه فرد است. با این توصیفات تنها تابعی که هم زوج و هم فرد محسوب میشود، تابع f(x)=0 است.
مثال: تابع زوج، فرد یا تابعی عادی است؟
جهت مشخص کردن زوج یا فرد بودن یک تابع، در قدم اول بایستی تابع (f(-x را محاسبه کرد. از این رو با قرار دادن x- بهجای x در تابع f داریم:
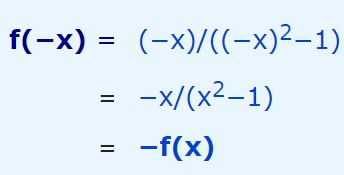
بنابراین (f(−x) = −f(x است. از این رو (f(x تابعی فرد محسوب میشود.
ویژگیهای توابع زوج و فرد
ویژگیهای توابع زوج و فرد دلیل جداسازی آنها از بقیه توابع است. از این ویژگیها در مباحث مختلف ریاضیات میتوان بهره برد.
در ادامه برخی از مهمترین ویژگیهای توابع زوج و فرد معرفی شدهاند.
- حاصل جمع دو تابع زوج، تابعی زوج است.
- حاصل جمع دو تابع فرد نیز تابعی فرد خواهد بود.
- با جمع کردن دو تابع زوج و فرد، به تابعی میرسیم که نه فرد و نه زوج است.
- حاصل ضرب دو تابع زوج نیز زوج خواهد بود.
- حاصل ضرب دو تابع فرد، تابعی زوج است.
- حاصل ضرب یک تابع زوج و یک تابع فرد، تابعی فرد خواهد بود.
آزمون توابع زوج و فرد
۱. کدام گزینه به طور دقیق معادله ریاضی تابع زوج را بیان میکند و نقش تقارن نسبت به محور y چیست؟
در تابع زوج معادله f(-x)=f(x) برقرار است و نمودار نسبت به محور y متقارن میماند.
برای تابع زوج معادله f(x)=-f(-x) برقرار میشود و تقارن نسبت به مبدا دیده میشود.
معادله تابع زوج f(-x)=-f(x) است و محور y تنها نقطه تقارن نیست.
در توابع زوج f(-x)=f(x+1) برقرار است و محور x تقارن دارد.
معادله درست برای تابع زوج، رابطه "f(-x)=f(x)" است. این معادله نشان میدهد که برای هر مقدار x، مقدار تابع برای قرینه x نسبت به محور y برابر با مقدار همان x است. این ویژگی دقیقا به معنای تقارن نمودار نسبت به محور y خواهد بود.
۲. اگر یک تابع از جمع یک تابع زوج و یک تابع فرد ساخته شود، براساس ویژگیهای جمع این نوع توابع، تابع جدید به کدام دسته تعلق دارد؟
تابع جدید همزمان زوج و فرد است.
تابع جدید حتما زوج است.
تابع جدید حتما فرد است.
تابع جدید نه زوج است و نه فرد.
طبق قواعد بیانشده، جمع یک تابع زوج با یک تابع فرد نتیجهای دارد که نه ویژگی تقارن نسبت به محور y را دارد و نه نسبت به مبدا. یعنی تابع حاصل، مانند حالت «تابع جدید نه زوج است و نه فرد»، به هیچیک از این دو دسته تعلق نمیگیرد. دیگر گزینهها نادرستند، چون تابع جدید با جمع تابع زوج یا فرد به تنهایی ساخته نشده است و نمیتواند خصوصیت هردوی آنها را داشته باشد یا همزمان هر دو باشد.













ممنون عالی بود
ممنونم ازتون کارم رو راه انداختید
دمت گرم اقای عوض زاده.عالی بود .لطفا مطالبی هم در مورد توابع زوج و فرد مثلثاتی قرار دهید با تشکر از شما.
با سلام و خسته نباشید ببینید ما یک دانشجو هستم که بعد از چند سال ترک تحصیل حالا ثبت نام کردم �خواستم اول مفهوم مفهوم یعنی درک مسئله از کجا شروع میشود و تعریف اولیه وقتی که ما برامون مفهوم نیست مثل اینکه نقاشی �کشیم با تشکر
ممنون بابت توضیحات مفید ومختصرتون
ممنون (:
خیلی خوب بود ممنونم
دمتون گرم واقعا
واقعا عالی بود .ممنون.
تو زمان کوتاه مفهوم رو میرسونین.این کارتون خیلی عالیه
من خیلی سپاسگزام از شما که خیلی مطالب خوبی را در بخش فرادرس ارائه می کنید الله متعال در برابر این کارتان اجر نامتناهی دهد
خیلی خوب بود ممنونم
دمتون گرم واقعا
مقسی مقسی بخاطر تموم پیگیریات مقسی
بسیار مفید بود .
خیلی متشکر از مطالب فوق العاده توووووون