تعیین حجم نمونه در تحلیل‌ های آماری — به زبان ساده

در انجام تحلیل‌های آماری، در بیشتر مواقع از نمونه آماری بهره می‌بریم. این کار البته باعث می‌شود که مقداری از اطلاعات که در جامعه آماری وجود دارد، نادیده گرفته شده و برآوردها و تخمین‌هایی که برای پارامتر جامعه آماری محاسبه می‌شوند با خطا همراه باشد. به منظور کاهش خطا به میزان مورد نظر و افزایش میزان اعتبار نتایج از تحلیل‌های آماری باید تعداد مناسبی نمونه انتخاب شود. از آنجایی که افزایش حجم نمونه باعث افزایش هزینه‌ و زمان تحلیل آماری می‌شود،‌ باید به حداقل حجم نمونه‌ای که خطایی معقول در برآورد پارامترهای جامعه دارد، قناعت کنیم.

برای آشنایی بیشتر با مفهوم جامعه آماری مطلب جامعه آماری — انواع داده و مقیاس‌های آن‌ها را مطالعه کنید. همچنین برای آگاهی از تعریف نمونه و کاربرد آن به مطلب نمونه‌گیری و بازنمونه‌گیری آماری (Sampling and Resampling) — به زبان ساده و برای آگاهی از روش‌های نمونه‌گیری به مطلب روش‌های نمونه‌گیری (Sampling) --- به زبان ساده مراجعه کنید.

تعیین حجم نمونه

برای محاسبه حجم نمونه مناسب برای تحلیل‌های آماری، باید نوع تحلیل از ابتدا مشخص باشد. همچنین باید توجه داشت که «نوع داده‌ها» (Data Type)، «توزیع آماری» (Distribution) و میزان پراکندگی‌ آن‌ها (Variance)، «میزان خطا» (Error Level) و همینطور سطح با معنایی (Confidence Level) در تعیین حجم نمونه موثر هستند.

تعیین حجم نمونه ممکن است به روش‌هایی که در ادامه به آن اشاره می‌شود، انجام پذیرد:

• تعیین حجم نمونه براساس تجربه: در این حالت محقق براساس اطلاعاتی که از توزیع احتمالی یا نوع داده‌ها دارد، حجم نمونه را تعیین می‌کند. برای مثال در این حالت اگر حجم نمونه کمتر از حد مورد نیاز باشد، ممکن است «فاصله اطمینان» (Confidence interval) ایجاد شده، دارای طولی بزرگتر از حد قابل قبول باشد که دقت برآورد را کاهش می‌دهد. همچنین با انتخاب حجم نمونه بزرگتر از مقدار مورد نیاز، هزینه‌های تحلیل‌های آماری بدون آنکه ضرورتی داشته باشد افزایش می‌دهد.
• تعیین حجم نمونه براساس میزان پراکندگی: با انتخاب مقدار واریانس به عنوان معیار پراکندگی برای برآوردگر، می‌توان حجم نمونه را انتخاب کرد. در چنین حالتی، برای رسیدن به واریانس کوچک‌تر (خطای کمتر) برای برآوردگر، احتیاج به حجم نمونه بیشتری نیز هست. در نتیجه اگر هدف تعیین کران‌های فاصله اطمینان باشد، می‌توان با انتخاب حجم نمونه بزرگ، به طول فاصله اطمینان کوچکتری نیز دست یافت.
• تعیین سطح با معنایی: با ثابت در نظر گرفتن میزان خطا، با افزایش مقدار سطح اطمینان یا سطح بامعنایی به نمونه بیشتری نیز نیاز داریم. در نتیجه باید بین میزان خطا و سطح معنی‌داری به یک تعادل رسید تا نمونه مناسب بدست آید. با انتخاب حداکثر میزان خطا و در نظر گرفتن سطح با معنایی مناسب به حداقل حجم نمونه خواهیم رسید.

در مسائل مربوط به تعیین حجم نمونه، اغلب توزیع داده‌ها را نرمال فرض می‌کنند. از طرفی می‌دانیم طبق قضیه حد مرکزی (Central Limit Theorem) و «قانون اعداد بزرگ» (law of Large Number) با افزایش حجم نمونه، میانگین بیشتر توزیع‌های آماری به سمت توزیع نرمال میل می‌کنند. بنابراین انتخاب توزیع نرمال برای داده‌ها کمی کاری غیر منطقی محسوب نمی‌شود بلکه فقط ممکن است حجم بزرگتری از نمونه به کار آید که باعث افزایش هزینه نمونه‌گیری می‌شود ولی در عمل خطا برآورد تغییری نخواهد کرد.

همانطور که گفته شد، از نمونه به منظور برآورد، انجام آزمون فرض آماری و یا تعیین فاصله اطمینان آماری استفاده می‌شود. ابتدا به تعیین حجم نمونه برای برآورد پارامترهای جامعه آماری می‌پردازیم. برای آشنایی با مباحث مربوط به فاصله اطمینان و آزمون‌های آماری بهتر است مطلب تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات  را قبلا مطالعه کرده باشید.

تعیین حجم نمونه به منظور برآورد نسبت

در بعضی از مواقع، برآورد نسبت در توزیع دو جمله‌ای مورد نظر است. برای مثال اگر بخواهیم نسبت ساکنین بالای ۶۵ سال در یک مجتمع مسکونی را برآورد کنیم، از برآورد نسبت استفاده می‌کنیم. در این حالت اگر X‌ متغیر تصادفی مربوط به تعداد ساکنینی باشد که بالای ۶۵ سال سن دارند، داریم $$p=\frac{X}{n}$$. پس می‌توان برآورد نسبت را به وسیله x به صورت زیر محاسبه کرد:

$$\widehat {p}=\frac{x}{n}$$

از طرفی می‌دانیم که واریانس توزیع دو جمله‌ای برابر است با $$Var(X)=np(1-p)$$ در نتیجه واریانس $$\widehat{p}$$‌ برابر است با $$\frac{p(1-p)}{n}$$. حداکثر مقدار واریانس $$\widehat{p}$$ نیز زمانی که $$\widehat{p}=0.5$$ باشد بدست می‌آید که برابر با 0.25 است. در نتیجه با استفاده از تقریب توزیع دو جمله‌ای با توزیع نرمال می‌توانیم بنویسیم:

$$\widehat{p}\sim N(p,0.25n)$$

به این ترتیب می‌توان یک فاصله اطمینان ۹۵٪ برای میانگین (نسبت) توزیع نرمال به صورت زیر تهیه کرد:

$$(\;\widehat{p}-1.96 ({\frac{0.25}{n}})^\frac{1}{2},\;\widehat{p}+1.96({\frac{0.25}{n}})^\frac{1}{2})$$

حال اگر طول این بازه اطمینان را برابر با W‌ در نظر بگیریم، می‌توان فاصله برآوردگر از پارامتر را W در نظر گرفت و به رابطه زیر رسید:

$$4\times({\frac{0.25}{n}})^\frac{1}{2}$$

با حل کردن این معادله برحسب n، به حداقل حجم نمونه مورد نیاز برای رسیدن به دقتی (خطای) برابر با W دست پیدا می‌کنیم. اگر با چنین حجمی از نمونه آزمون فرض انجام دهیم خطای نوع اول آزمون ($$\alpha$$) حداکثر برابر با ۵٪ است زیرا در مرحله قبل یک فاصله اطمینان ۹۵٪ را ملاک تعیین حجم نمونه قرار دادیم.

رابطه بین W و n به شکل ساده‌تر به صورت زیر خواهد بود.

$$n=\frac{4}{W^2}$$

برای مثال برای تعیین حجم نمونه به منظور برآورد نسبت در یک جامعه آماری با طول فاصله اطمینانی برابر با 0.1 محاسبات زیر را انجام می‌دهیم.:

$$n=\frac{4}{(0.1)^2}=4\times 100=400$$

همچنین اگر می‌خواهید که دقت بیشتری داشته باشید و مثلا طول فاصله  اطمینان  برابر با 0.05 باشد حجم نمونه لازم به 1600 خواهد رسید.
نکته: می‌دانیم میانگین داده‌های باینری همان نسبت را نشان می‌دهد.

 تعیین حجم نمونه به منظور برآورد میانگین

در اینجا فرض می‌کنیم که هدف، برآورد میانگین جامعه آماری است و واریانس نیز معلوم و برابر با $$\sigma ^2$$ است. همچنین نمونه‌ها نیز مستقل فرض شده‌اند.

با توجه به محاسباتی که برای فاصله اطمینان برای توزیع نرمال در قسمت قبل دیدم، می‌توانیم در این حالت نیز بنویسیم:

$$(\overline{x}-\dfrac{1.96\times \sigma}{\sqrt{n}},\;\overline{x}+\dfrac{1.96\times \sigma}{\sqrt{n}})$$

به این ترتیب با طی کردن محاسباتی که در قسمت برآورد نسبت گفته شده، می‌توان رابطه‌ بین W (طول فاصله اطمینان) و حجم نمونه را پیدا کرد:

$$W=\dfrac{4\sigma}{\sqrt{n}}$$

در نتیجه حداقل حجم نمونه برای رسیدن به چنین دقتی در آزمون آماری با احتمال خطای نوع اول 0.05 برابر است با

$$n=\frac{16\sigma^2}{W^2}$$

برای مثال اگر هدف بررسی میزان فشار خون باشد و بخواهیم بک فاصله اطمینان با طولی برابر با ۶ واحد ایجاد کنیم، با فرض اینکه فشار خون دارای انحراف استانداردی برابر با ۱۵ واحد است، احتیاج به یک نمونه ۱۰۰ تایی داریم، زیرا:

$$n=\frac{16(15^2)}{6^2}=100$$

تعیین حجم نمونه با توجه به توان آزمون

در روش‌های پیشین برای تعیین حجم نمونه، توجه بر احتمال خطای نوع اول ($$\alpha$$) بود که در تعیین فاصله اطمینان از آن استفاده می‌شود.

ولی اگر هدف تعیین حجم نمونه برای رسیدن به توان آزمون $$(1 -\beta)$$ مناسب باشد، از شیوه‌های محاسباتی دیگری کمک می‌گیریم. در ادامه با این روش‌ها آشنا شده و نحوه محاسبه حجم نمونه را مشخص می‌کنیم.

نکته: اگر احتمال خطای نوع دوم را با $$\beta$$ نشان دهیم، مقدار $$1 - \beta$$ را توان آزمون می‌نامند. هرچه حجم نمونه افزایش یابد، توان آزمون نیز بیشتر خواهد شد.

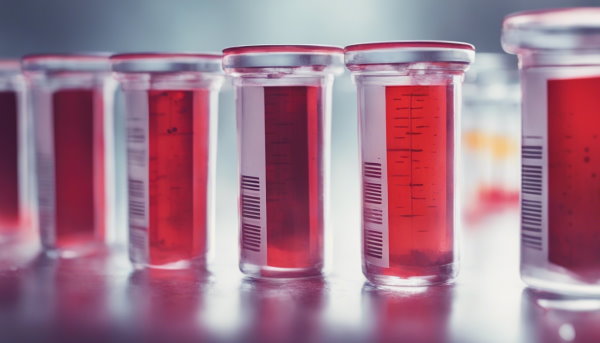
استفاده از جدول‌های حجم نمونه و توان آزمون

معمولا به کمک روش‌های محاسباتی، جدول‌هایی برای تعیین حجم نمونه با توجه به نوع آزمون، میزان توان آزمون، و احتمال خطای نوع اول ($$\alpha$$) ساخته شده است. در زیر یک نمونه از جدول تعیین حجم نمونه قرار گرفته است که برای آزمون مقایسه میانگین در دو گروه کنترل و آزمودنی به کار می‌رود. احتمال خطای نوع اول برای این جدول 0.05 است.

در ستون اول مقدار توان آزمون و در ستون‌های دوم و تا چهارم نیز حجم نمونه مورد نیاز نوشته شده است. در سطر اول مربوط به ستون‌های دوم تا چهارم نیز میزان خطای نسبی (Cohen's d) گروه کنترل نسبت به گروه آزمودنی دیده می‌شود که گاهی به آن اندازه اثر نیز می‌گویند. برای مثال در ستون دوم در اولین سطر مقدار که مقدار برابر با 0.2 دیده می‌شود درصد خطا یا فاصله میانگین دو گروه نسبت به انحراف معیار به صورت زیر در نظر گرفته شده است:

$$Cohen's\;d=\dfrac{(M_{exp} -M_{cont})}{SD}$$

که در آن، $$M_{exp}$$‌ میانگین ویژگی گروه آزمودنی و $$M_{cont}$$ میانگین ویژگی گروه گنترل و $$SD$$ نیز انحراف معیار مربوط به ویژگی مورد نظر در جامعه آماری است.

بنابراین برای انجام آزمون مقایسه میانگین بین دو گروه آزمودنی و کنترل با حجم یکسان با توان 0.99 و درصد خطای 0.2 احتیاج به 920 نمونه برای هر گروه داریم. در نتیجه تعداد مشاهدات در کل برابر است با $$2\times 920=1840$$ نفر. به نظر می‌رسد برای بالا بردن توان آزمون باید از حجم نمونه بزرگتری استفاده کنیم. البته این قاعده همیشه برقرار است، یعنی برای دقت آزمون (توان بیشتر آزمون) باید حجم نمونه را افزایش داد.

تعیین حجم نمونه با استفاده از معادله منابع Mead

در بررسی و تحقیقات آزمایشگاهی بخصوص روی جانوران، از معادله منابع Mead برای تعیین حجم نمونه استفاده می‌شود. هر چند ممکن است این روش دقت زیادی تعیین حجم نمونه نداشته باشد ولی در مواردی که واریانس یا انحراف استاندارد جامعه و همچنین میانگین دو گروه آزمودنی و کنترل در دسترس نباشد راهگشا است.

این معادله به صورت زیر است:

$$E=N-B-T$$

پارامترهای این معادله در زیر معرفی شده‌اند:

• N: درجه آزادی مشاهدات (تعداد مشاهدات یا واحدهای مورد مطالعه)
• B: درجه آزادی مولفه بلوکی
• T: درجه آزادی تیمارها
• E: درجه آزادی خطای مولفه‌ها است که باید بین ۱۰ تا ۲۰ باشد.

برای محاسبه معادله منابع Mead کافی است که از درجه آزادی هر یک از مفاهیم مربوطه استفاده شود. در نتیجه همانطور که در ادامه خواهید دید، از هر کدام از پارامترهای گفته شده یک واحد کسر می‌شود تا درجه آزادی مربوطه محاسبه شود.

برای مثال اگر در یک آزمایشگاه حیوانات، از 24 حیوان مختلف که در دو دسته اهلی و وحشی (B=2-1) یک طرح تحقیقاتی با ۴ نوع رژیم غذایی متفاوت که تیمار نامیده می‌شود (T=4-1) انجام شود، مقدار درجه آزادی E برابر خواهد بود با:

$$(24-1)+(2-1)+(4-1)=23-1-3=19$$

که در محدوده ۱۰ تا ۲۰ قرار دارد. پس چنین طرح آزمایشی با این حجم نمونه (۱۹ جانور)، می‌تواند توان آزمون مناسبی را برای محقق به همراه داشته باشد.

تابع توزیع احتمال

در این حالت با توجه به آزمون فرض آماری، تعداد نمونه مناسب براساس توان آزمون محاسبه می‌شود.

فرض کنیم $$X_1,X_2,\ldots,X_n$$ یک نمونه تصادفی مستقل دارای توزیع نرمال با میانگین نامعلوم $$\mu$$ و واریانس مشخص $$\sigma^2$$ باشند. همچنین در نظر بگیرید که فرضیات مربوط به آزمون فرض آماری به صورت زیر نوشته شده است:

$$H_0: \mu=0$$

در مقابل:

$$H_1: \mu=\mu^*$$

مقدار مثبت $$\mu^*$$ حداقل مقدار اختلاف معنادار نسبت به صفر در نظر گرفته می‌شود. همانطور که می‌دانید فرضیات این آزمون ساده و یک طرفه است. زیرا فرض کرده‌ایم که $$\mu-\mu^*>0$$‌ است. حال احتمال خطای نوع اول چنین آزمونی را محاسبه می‌کنیم.

$$Pr(\;\overline{x}>z_{\alpha}\frac{\sigma}{\sqrt{n}}\;|\;H_۰ \;is\;true)=\alpha$$

در نتیجه اگر میانگین نمونه تصادفی ($$\overline{x}$$) بزرگتر از مقدار $$z_{\alpha}\frac{\sigma}{\sqrt{n}}$$ باشد فرض صفر رد می‌شود.

حال توان چنین آزمون را توسط محاسبه زیر بدست می‌آوریم:

$$Pr(\;\overline{x}>z_{\alpha}\frac{\sigma}{\sqrt{n}}|\;H_1 \;is\;true)= 1-\beta$$

با توجه به فرض مقابل می‌توان توزیع داده‌ها را نرمال با میانگین $$\mu^*$$ در نظر گرفت در نتیجه مقدار این احتمال برابر است:

$$1-\Phi(z_{\alpha}\frac{\sigma}{\sqrt{n}})$$

که در آن $$\Phi$$ تابع توزیع احتمال نرمال استاندارد است. به این ترتیب می‌توان حداقل تعداد نمونه برای رسیدن به توان آزمون $$1-\beta$$ را به صورت زیر نوشت:

$$n\geq (\dfrac{z_{\alpha}+\Phi^{-1}(1-\beta)}{\dfrac{\mu^*}{\sigma}})^2$$

که منظور از $$\Phi^{-1}$$ معکوس تابع توزیع نرمال استاندارد است که همان صدک محسوب می‌شود.

بنابراین اگر $$\mu_0=0.2$$ و انحراف استاندارد جامعه نرمال برابر با 5 و احتمال خطای نوع اول نیز 0.05 در نظر گرفته شود برای چنین آزمونی اگر بخواهیم میزان توان آزمون برابر با 0.9 باشد، حداقل حجم نمونه برابر است با 6567 که با توجه به محاسبات زیر حاصل می‌شود:

$$n\geq (\dfrac{1.96+\Phi^{-1}(0.9)}{\dfrac{0.2}{5}})^2=6567$$

نمونه‌گیری طبقه‌ای و تعیین حجم نمونه‌ها

زمانی که بتوان جامعه را به K زیرجامعه تفکیک کرد، روش نمونه‌گیری طبقه‌ای به کار گرفته می‌شود. هرچند ممکن است این روش هزینه بیشتری نسبت به نمونه‌گیری تصادفی ساده داشته باشد ولی به علت دقت بیشتر این روش در نتایج تحلیل‌های آماری استفاده از آن توصیه می‌شود.

علت این است که در این روش از اطلاعات اضافه که در مورد زیرجامعه‌ها وجود دارد استفاده خواهد شد.

در طرح‌های نمونه‌گیری پیچیده مانند روش نمونه‌گیری طبقه‌ای، نمونه‌ها به زیرنمونه‌ها، قابل تفکیک هستند. بنابراین اگر K تعداد طبقات در یک طرح نمونه‌گیری باشد، آنگاه $$n_i,\;i=1,2,\ldots,K$$  را می‌توان حجم نمونه در طبقه iام در نظر گرفت بطوری که مجموع حجم این زیرنمونه‌ها برابر با حجم نمونه نهایی خواهد بود:

$$n=\sum_{i=1}^K n_{i}=n_1+n_2+\ldots+n_K$$

مشخص کردن حجم این زیرنمونه‌ها به شیوه‌های مختلفی امکان پذیر است. یکی از این روش‌ها استفاده از اطلاعاتی است که اندازه جامعه و زیرجامعه‌ها دارد. فرض کنید از قبل می‌دانیم که باید از یک جامعه با حجم N یک نمونه nتایی تهیه کنیم. از طرفی می‌دانیم که اندازه زیرجامعه iام نیز برابر است با $$N_i$$. پس می‌توان به نسبت حجم زیرجامعه به کل جامعه نیز اندازه نمونه از زیرطبقه را مشخص کرد. بنابراین خواهیم داشت:

$$n_j=(\dfrac{N_i}{N})\times n$$

همچنین با توجه به برآورد میانگین و خطای برآورد میانگین جامعه نیز اندازه نمونه برای هر زیرطبقه قابل تعیین است. برای این کار کافی است که میانگین و واریانس جامعه را براساس طبقات برآورد کرد. یک روش برای چنین برآوردی استفاده از میانگین وزنی است.

اگر $$W_i$$ را نسبت اندازه زیرجامعه به کل جامعه در نظر بگیریم، می‌توان میانگین و خطای میانگین را از طریق این وزن‌ها برآورد کرد. بنابراین اگر $$N_i$$ تعداد اعضای زیر جامعه iام باشد، وزن برای زیر جامعه iام را به صورت زیر در نظر می‌گیریم:

$$W_i=\dfrac{N_i}{N}$$

در چنین حالتی می‌توان برآورد میانگین را به صورت زیر نوشت:

$$\overline{x}_w=\sum_{i=1}^KW_i\overline{x_i}$$

همچنین واریانس این برآوردگر نیز از برحسب این وزن‌ها برابر خواهد بود با:

$$Var(\;\overline{x}_w)=\sum_{i=1}^K W_i^2 Var(\;\overline{x}_i)$$

از طرفی، برآورد واریانس اصلاح شده برای میانگین وزنی به صورت زیر نوشته می‌شود:

$$Var(\;\overline{x}_w)=\sum_{i=1}^K W_i^2 Var(\;\overline{x}_i)(\dfrac{1}{n_i}-\dfrac{1}{N_i})$$

این مجموع (واریانس برآوردگر میانگین) زمانی حداقل ممکن را خواهد داشت که وزن‌ها متناسب با واریانس زیرنمونه‌ها باشند، یعنی اگر $$S_i$$ انحراف استاندارد میانگین زیرنمونه iام باشد، داریم:

$$\dfrac{n_i}{N_i}=h\;S_i$$

ضریب h به علت نرمال‌سازی به کار رفته بطوری که با حجم ثابت n برای نمونه داشته باشیم $$n_1+n_2+\ldots +n_K=n$$.

اگر هزینه نمونه‌گیری در هر زیر گروه را نیز با $$C_i$$‌ نشان دهیم، می‌توان فرمول زیر را برای تعیین حجم زیرنمونه‌ها با توجه به خطای میانگین (انحراف استاندارد میانگین) و هزینه نمونه‌گیری در هر زیرنمونه به صورت زیر نوشت:

$$\dfrac{n_i}{N_i}=\dfrac{h\;S_i}{\sqrt{C_i}}$$

پس با در نظر گرفتن حجم برابر زیرجامعه‌ها، اندازه زیرنمونه‌ها با خطای میانگین هر زیرنمونه رابطه مستقیم و با هزینه نمونه‌گیری رابطه معکوس دارد.

مثال

فرض کنید یک جامعه به 3 زیرطبقه قابل تفکیک باشد. هر زیرطبقه دارای اندازه‌ای به ترتیب برابر با 1000، 5000 و 10000 است. اگر بخواهیم خطای میانگین برای هر زیرجامعه به ترتیب بربر با 1، 5 و 10 باشد با توجه به حجم نمونه کلی 100، محاسبات برای تعیین حجم زیرنمونه‌ها با در نظر گرفتن هزینه ثابت ۱۰۰ تومان برای نمونه‌گیری، به صورت زیر خواهد بود:

$$\dfrac{n_۱}{1000}=\dfrac{h \times 1i}{10}=\dfrac{h}{10}\rightarrow n_1=1000\times \dfrac{h}{10}=100 h$$

$$\dfrac{n_2}{5000}=\dfrac{h \times 5}{10}=\dfrac{5h}{10}\rightarrow n_2=5000\times \dfrac{5h}{10}=2500 h$$

$$\dfrac{n_۱}{10000}=\dfrac{h \times 10i}{10}=\dfrac{10h}{10}\rightarrow n_3=10000\times \dfrac{10h}{10}=10000 h$$

از طرفی باید حجم نمونه کلی برابر با ۱۰۰ باشد، پس خواهیم داشت:

$$n_1+n_2+n_3=100h+2500h+1000h=100\rightarrow h=\dfrac{100}{12600}=0.008$$

پس اندازه زیرنمونه اول برابر است با 0.79 و برای زیرنمونه دوم برابر با 19.84 و برای زیرنمونه سوم نیز برابر با 79.37 خواهد بود. از طرفی جمع این زیرنمونه‌ها نیز برابر با ۱۰۰ است. همانطور که دیده می‌شود، از زیرجامعه‌ای که دارای خطای میانگین بیشتری است اندازه نمونه بزرگتری نیز تهیه شده است.

تعیین حجم نمونه در تحقیقات کیفی

در تحقیقات کیفی، در بیشتر موارد تعیین حجم نمونه به هدف تحقیق و نظر محقق بستگی دارد. تجربه و شناخت از جامعه آماری در چنین مواقعی تاثیر زیادی در تعیین حجم نمونه در بررسی‌های کیفی دارد.

البته گاهی حجم نمونه را با تکرار عمل نمونه‌گیری تا رسیدن به یک آستانه از قبل تعیین شده مشخص می‌کنند. برای مثال در هنگام بررسی بیماری و تخمین میزان شیوع یک نوع بیماری، نمونه‌گیری تا رسیدن به اولین فردی که علائم بیماری را دارد ادامه پیدا می‌کند.