مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
نمودار مکان هندسی ریشهها، ابزار بسیار مفیدی برای پیشبینی رفتار سیستم حلقه بسته بهازای تغییر برخی پارامترهای سیستم (معمولاً بهره) است. در این روش ترسیمی که در سال 1948 توسط «والتر ایوانز» (Walter R. Evans) ابداع شد، میتوان با استفاده از قطبها و صفرهای سیستم حلقه باز، پایداری سیستم حلقه بسته را بررسی کرد. مکان هندسی ریشهها، علاوه بر تحلیل سیستم، در طراحی کنترل کننده نیز کاربرد دارد.

در این آموزش، با نحوه ترسیم «مکان هندسی ریشهها» (Root Locus) و برخی ویژگیهای آن آشنا خواهیم شد.
یک مثال ساده
برای درک اهمیت و نحوه رسم نمودار مکان ریشهها، ابتدا رفتار یک سیستم کنترل را بررسی میکنیم. فرض کنید سیستم تحت کنترل با تابع تبدیل زیر تعریف شده باشد:
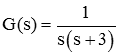
این سیستم را با یک کنترلکننده ساده تناسبی کنترل میکنیم که در آن، ورودی سیستم G بهصورت تناسبی با اعمال بهره K به اختلاف بین ورودی و خروجی کنترل میشود.

تابع تبدیل حلقه باز، برابر با است. تابع تبدیل حلقه بسته نیز بهصورت زیر محاسبه میشود:
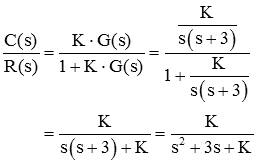
سعی و خطا
در اینجا میخواهیم ببینیم رفتار سیستم با تغییر K چگونه خواهد بود. بنابراین، چند مقدار مختلف را برای K امتحان میکنیم. سه مقدار اختیاری 1، 10 و 100 را انتخاب میکنیم.
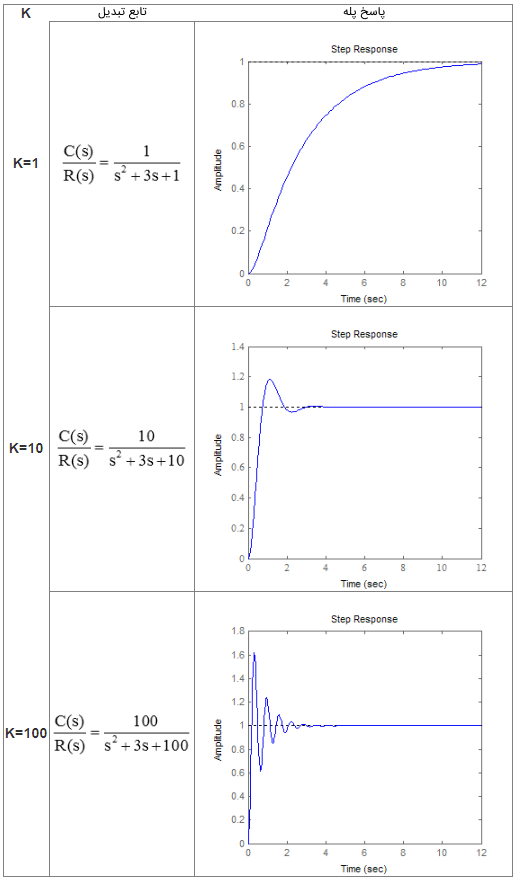
همانگونه که از شکل بالا مشخص است، پاسخ سیستم برای بسیار کند، برای بسیار نوسانی و برای نسبتاً مطلوب است؛ البته در این حالت، بهتر است مقدار فراجهش کمتر باشد. واضح است که این روش سعی و خطا برای تعیین مقدار مناسب K، زمانبر است.
یک روش پیشرفتهتر
یک روش تحلیلیتر برای پیدا کردن مقدار مناسب K، پیدا کردن قطبهای تابع تبدیل حلقه بسته است. از آنجایی که تابع تبدیل بالا، مرتبه دوم است، میتوانیم ریشههای مخرج آن را بهسادگی محاسبه کنیم:
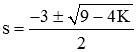
پاسخ سیستم بهازای ، فرامیرا، بهازای فرومیرا و بهزای میرای بحرانی خواهد بود. اگر بخواهیم پاسخی فرومیرا با میرایی داشته باشیم، باید اندازه بخشهای حقیقی و موهومی ریشهها را مساوی قرار دهیم. با ریشههای زیر شروع میکنیم:
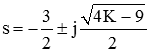
با برابر در نظر گرفتن بخش حقیقی و موهومی، داریم:
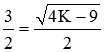
که از این رابطه، مقدار K بهدست میآید:
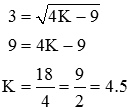
با مقدار ، تابع تبدیل و پاسخ پله سیستم بهصورت زیر خواهند بود:
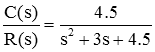
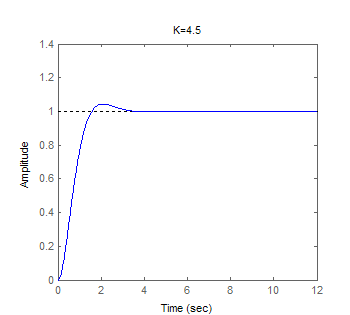
هرچند این روش محاسبه بهره برای سیستمهای ساده بهآسانی قابل انجام است، اما اعمال آن به سیستمهای پیچیدهتر، با مشکل همراه خواهد بود. مثلاً تابع تبدیل زیر را در نظر بگیرید که بهره مناسب را برای کنترل آن نمیتوان با روش بالا بهآسانی محاسبه کرد.
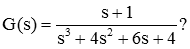
بنابراین، به روش دیگری برای کار با چنین سیستمهایی نیاز داریم.
مکان هندسی ریشهها
برای مثال سادهای که بیان شد، میتوان مکان ریشهها را تعیین و مقدار K را برای پاسخ مناسب انتخاب کرد. اما برای سیستمهای پیچیدهتر، این کار سرراست نیست و به یک روش عمومیتر برای حل این مسائل نیاز است.
این روش، «مکان هندسی ریشهها» (Root locus) نامیده میشود. با استفاده از تکنیک مکان هندسی ریشهها، میتوانیم مسیر ریشهها را با تغییر پارامتر مورد نظر (معمولاً بهره)، رسم کنیم.
مجدداً مثال بالا را در نظر بگیرید:
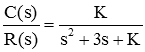
اگر بخواهیم مسیر ریشهها را بهازای تغییرات K رسم کنیم، میتوانیم ریشههای معادله زیر را برای مقادیر مختلف K حل کنیم:
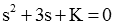
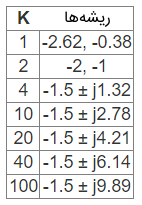
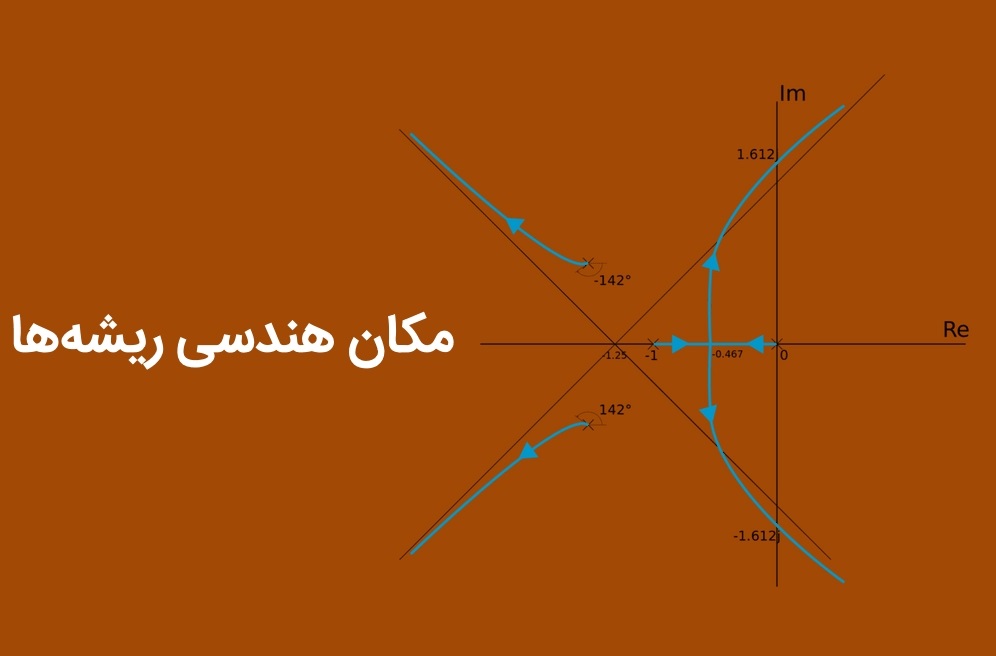
این مقادیر در شکل زیر رسم شدهاند (در ریشههای مختلط، مقدار K فقط برای بخش موهومی مثبت نشان داده شده است).
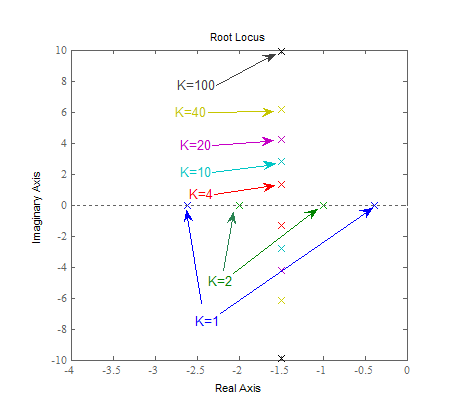
شکل بالا حاوی اطلاعات بسیار مفیدی است. از این شکل میتوان فهمید که سیستم از حالت فرامیرا برای Kهای کوچک شروع شده و با افزایش مقدار K، فرومیرا خواهد شد. اگر افزایش K ادامه پیدا کند، سیستم فرومیراتر میشود.
نمودار مکان هندسی ریشهها نیز تعمیمی از همین شکل بالا است. این نمودار، مسیر ریشهها را بهازای تغییر K نشان میدهد، اما مقدار دقیق K را مشخص نمیکند. اهمیت این روش تا حدی است که در متلب، دستوری برای رسم نمودار آن وجود دارد. نمودار مکان ریشه مثال مورد بحث بالا در نرمافزار متلب، بهصورت زیر قابل رسم است:
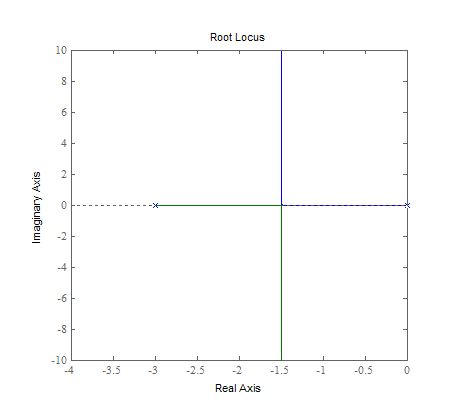
نقطه شروع ریشهها، است که با دو علامت ضرب () کوچک در و نشان داده شده است. با افزایش K، دو ریشه بهصورت افقی به سمت یکدیگر حرکت خواهند کرد و در به هم خواهند رسید. سپس بهصورت عمودی از هم دور خواهند شد.
با اینکه مقدار K در نمودار تعیین نشده است، میتوان آن را بهآسانی محاسبه کرد. برای مثال، اگر بخواهیم مقدار K را در بیابیم، میتوانیم از معادله مشخصه تابع تبدیل استفاده کنیم:
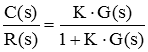
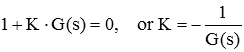
معادله فوق، برای هر نقطهای از مکان ریشهها صادق است. بهطور خاص، در داریم:
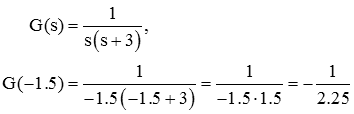
از محاسبات بالا میتوانیم برای تعیین مقدار K مورد نظر استفاده کنیم:
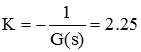
ترسیم مکان هندسی ریشهها
در این بخش، قواعد رسم مکان هندسی ریشهها را بیان خواهیم کرد. البته، گاهی همه این قواعد برای رسم مکان ریشهها قابل اعمال نیستند. گامهای رسم مکان ریشهها به شرح زیر است:
- کسب اطلاعات درباره تابع تبدیل
- قواعد ترسیم:
- تقارن
- تعداد شاخهها
- نقاط شروع و پایان
- مکان روی محور حقیقی
- مجانبها وقتی
- نقاط شکست (خروج از قطب و ورود به صفر)
- زاویه خروج از قطب
- زاویه ورود به صفز
- مکانهای قطع محور موهومی
- تعیین محل قطبها با داشتن K
- تعیین مقدار K با داشتن محل قطبها
کسب اطلاعات درباره تابع تبدیل
تابع تبدیل حلقه بسته سیستم بهصورت زیر است:
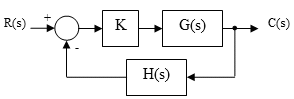
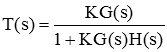
بنابراین، منحنی مشخصه زیر را خواهیم داشت:
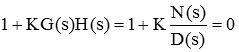
میتوانیم بهره حلقه باز را بهعنوان نسبت چندجملهایها بنویسیم (فرض میکنیم ، و و معمولاً ). چندجملهای صورت از درجه m است و ریشههای آن در قرار دارند. چندجملهای مخرج از درجه n است و ریشههای آن در قرار دارند. اختلاف بین چندجملهایهای صورت و مخرج برابر است. فرض میکنیم تابع تبدیل سره باشد یا به عبارت دیگر .
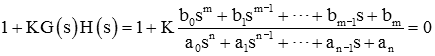
میتوان بهره حلقه را بهشکل فاکتورگیری شده زیر نوشت:
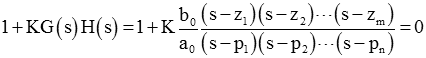
اگر K تغییر کند، محل قطبهای حلقه بسته (یا همان صفرهای معادله مشخصه) نیز تغییر میکند.
با کمی تغییر معادله مشخصه بهصورت زیر میتوانیم نتایج مفیدی از آن بهدست آوریم:
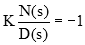
از آنجایی که این معادله مقادیر مختلط دارد، اندازه و فاز دو طرف آن باید برابر باشد. شرط اندازه بهصورت زیر بیان میشود:
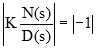
از آنجایی که ، میتوانیم بنویسیم:
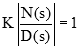
تساوی فاز دو طرف نیز بهشکل زیر نوشته میشود:
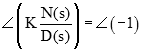
به دلیل آنکه ، میتوان از فاز صرفنظر کرد. زاویه نیز ضریب فرد است.
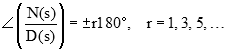
قواعد ترسیم
در ادامه به قواعد ترسیم در همین رابطه میپردازیم:
قاعده 1: تقارن
از آنجایی که ضرایب معادله مشخصه حقیقی است، هر ریشهای از آن که حقیقی نباشد، مختلط مزدوج و نسبت به محور حقیقی، متقارن است. میدانیم که مکان هندسی ریشهها، نمودار ریشههای معادله مشخصه بهازای تغییرات K است و در نتیجه نسبت به محور حقیقی متقارن است.
قاعده ۱: مکان ریشهها نسبت به محور حقیقی متقارن است.
قاعده ۲: تعداد شاخهها
از آنجایی که مکان ریشهها، نمودار ریشههای معادله مشخصه بهازای تغییر K، و مرتبه معادله مشخصه برابر با مخرج تابع تبدیل حلقه باز است، تعداد شاخهها برابر با n خواهد بود که مرتبه چندجملهای مخرج است.
قاعده ۲: تعداد شاخههای مکان هندسی ریشهها برابر با درجه معادله مشخصه است.
قاعده ۳: نقاط ابتدا و انتها
با در نظر گرفتن شرط اندازه زیر:
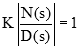
واضح است که اگر ، تنها راهی که سمت چپ معادله برابر با ۱ باشد، این است که مقدار قدر مطلق به بینهایت میل کند. این وضعیت زمانی رخ میدهد که . بنابراین، قطبهای حلقه باز، نقاط شروع مکان هندسی هستند (وقتی ).
همچنین اگر ، سمت چپ معادله در صورتی برابر با 1 خواهد بود که قدر مطلق به صفر میل کند و زمانی رخ میدهد که . این موضوع زمانی اتفاق میافتد که و درجه مخرج بیشتر از درجه صورت باشد. بنابراین، صفرهای حلقه باز (که در و احتمالاً هنگامی که رخ میدهند) نقاط پایانی مکان هستند (وقتی ).
قاعده ۳: مکان هندسی ریشهها، از قطبهای بهره حلقه (وقتی ) شروع شده و در صفرها به پایان میرسد (وقتی ). توجه کنید که وقتی ، تعداد q صفر حلقه باز وجود دارد.
قاعده ۴: مکان هندسی روی محور حقیقی
شرط زاویه را در نظر بگیرید:
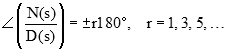
با نوشتن چندجملهایهای صورت و مخرج داریم:
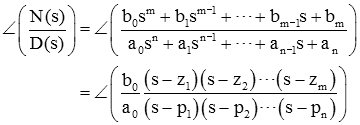
از آنجایی که ، و معمولاً است، داریم:
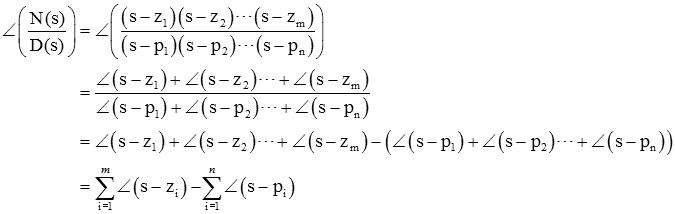
بنابراین، معیار زاویه را میتوان بهصورت زیر نوشت:
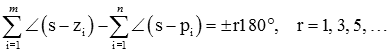
اکنون، به زاویه بین نقطه s (بردار قرمز) و نقطه z (بردار آبی) روی محور حقیقی توجه کنید. نمودارهای زیر، بردار s-z (بردار سبز) را برای مواردی که s سمت راست z یا سمت چپ آن باشد، نشان میدهند.
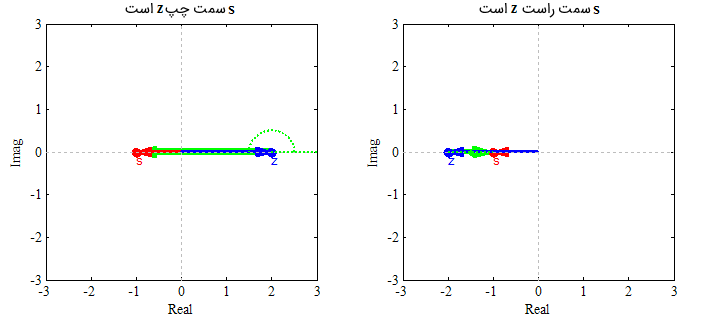
از شکلهای بالا در مییابیم که وقتی s سمت چپ z است، زاویه بردار s-z برابر با 180 درجه (یا هر مضرب فردی از آن) خواهد بود. همچنین در حالتی که s در سمت راست z قرار میگیرد، زاویه s-z صفر یا مضرب زوجی از 180 درجه است.
اکنون، قطب و صفرهای مختلط مزدوج را بررسی میکنیم. بدین منظور، شکل زیر را در نظر بگیرید.
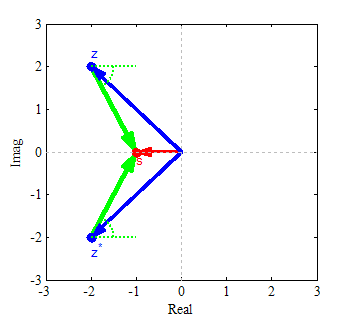
در نمودار بالا، بردار s قرمز، و بردارهای z و مزدوج آن () آبی هستند. همچنین بردار s-z با رنگ سبز نشان داده شده است. واضح است که زاویههای z و برابر و مخالف یکدیگر هستند، در نتیجه همدیگر را خنثی میکنند. بنابراین، صفرها و قطبهای مختلط مزدوج را در نظر نمیگیریم و فقط قطبها و صفرهای حقیقی را بررسی میکنیم.
یک بار دیگر معیار زاویه را در نظر بگیرید:
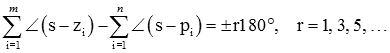
از آنجایی که در رابطه بالا، نتیجه تفاضل مجموع زوایای صفرها از مجموع زوایای قطبها ضریب فردی از است، نقطه s روی محور حقیقی، تنها زمانی در مکان ریشه واقع میشود که سمت راست آن، تعداد فردی صفر و قطب روی محور وجود داشته باشد.
قاعده ۴: مکان ریشهها روی محور حقیقی، در جایی وجود دارد که تعداد فردی قطب و صفر در سمت راست آن وجود داشته باشد.
قاعده ۵: مجانبها
اگر (به عبارت دیگر، درجه چندجملهای مخرج حلقه باز، بزرگتر از درجه چندجملهای صورت باشد)، حلقه باز، q صفر در بینهایت دارد. میتوان از تقریبهایی برای توصیف رفتار قطبهای حلقه بسته در بینهایت استفاده کرد. اگر باشد، نیازی به این مرحله نیست.
برای محاسبه زاویه مجانبها معمولاً از تقریبهایی استفاده میشود که در اینجا از پرداختن به جزئیات و نحوه محاسبه آنها خودداری و نتیجه را بیان میکنیم.
قاعده 5: اگر باشد،
- مجانبها محور حقیقی را در نقطه زیر قطع میکنند:
- زاویه مجانبها را نیز میتوان با استفاده از رابطه زیر بهدست آورد:
قاعده ۶: نقاط شکست
برای یافتن نقاطی که مکان هندسی ریشهها از محور حقیقی خارج یا به آن وارد میشود، باید دو قطب مجاور یا دو صفر مجاور روی محور وجود داشته باشد. واضح است که در نقاط شکست، ریشهها به هم میرسند و به یک ریشه تکراری تبدیل خواهند شد. وقتی یک چندجملهای ریشه مکرر داشته باشد، علاوه بر خود چندجملهای، مشتق آن نیز برابر با صفر است. بنابراین، ابتدا معادله مشخصه را در نظر میگیریم:
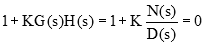
در نقاط شکست، مشتق معادله مشخصه برابر با صفر است:
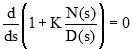
اگر عملیات مشتقگیری را انجام دهیم، معادله زیر بهدست میآید:
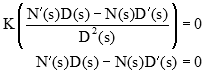
قاعده ۶: نقاط شکست روی محور حقیقی در مکان هندسی ریشهها، از معادله زیر بهدست میآید:
قاعده 7: زاویه خروج از قطب مختلط
میدانیم اگر ، یک قطب ساده روی محور حقیقی داشته باشد، وقتی ، مکان هندسی روی محور از قطب خارج میشود. هرچند، اگر قطب مختلط باشد، ممکن است با هر زاویهای خارج شود. برای یافتن زاویه خروج مکان هندسی در قطب مختلط، از معیار زاویه استفاده میکنیم:
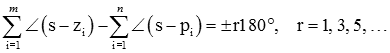
برای پیدا کردن زاویه خروج از قطب ، میتوانیم معیار زاویه را با اعمال زاویه بین مکان ریشه و بهصورت زیر بنویسیم:
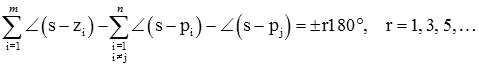
یا
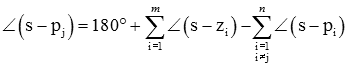
از آنجایی که پاسخها برای همه مقادیر r یکسان است، در این معادله قرار میدهیم. اکنون، اگر نقطه s را روی مکان هندسی در نظر بگیریم که بسیار نزدیک به باشد، آنگاه همه عبارات سمت راست را میتوان با زاویه بین قطب یا صفر و تقریب زد. به عبارت دیگر، اگر s بسیار نزدیک به باشد، میتوان معیار زاویه را تقریب زد:
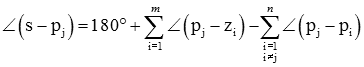
شکل زیر، مثالی از نمودار مکان هندسی ریشهها را نشان میدهد که در آن، تابع یک صفر در و سه قطب در و دارد.
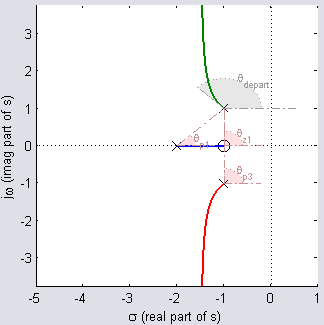
برای یافتن زاویه خروج از قطب در (که نامیده میشود)، نقطهای را روی مکان هندسی انتخاب میکنیم که بسیار نزدیک به باشد و سپس زاویههای آن نسبت به صفر و قطبها را مییابیم.
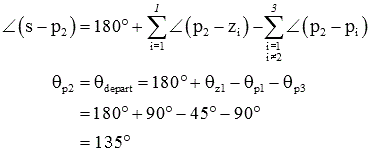
قاعده ۷: زاویه خروج از قطب مختلط برابر با 180 درجه بهعلاوه مجموع زوایای بین و تمام صفرها، منهای مجموع زوایای بین و قطبهای دیگر است:
قاعده ۸: زاویه ورود به صفر مختلط
میدانیم اگر بهره حلقه یک صفر ساده روی محور حقیقی داشته باشد، وقتی ، مکان ریشهها روی محور به آن خواهد رسید. اما، اگر صفر مختلط باشد، ممکن است مکان ریشهها با هر زاویهای به آن برسد. برای پیدا کردن این زاویه، از معیار زاویه استفاده میکنیم:
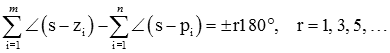
برای یافتن زاویه رسیدن مکان به صفر ، معیار زاویه را بهصورت زیر بازنویسی میکنیم:
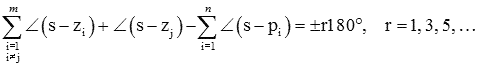
یا
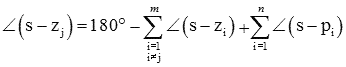
در این معادله، r را برابر ۱ در نظر میگیریم، زیرا نتیجه برای همه مقادیر r یکسان است. اکنون، اگر نقطه s را روی مکان که بسیار نزدیک است در نظر بگیریم، میتوانیم همه جملات سمت راست را با زاویه بین قطب یا صفر و تقریب بزنیم. به عبارت دیگر، اگر s بسیار نزدیک به باشد، میتوان معیار زاویه را بهصورت زیر تقریب زد:
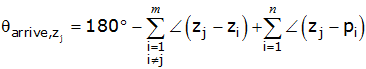
قاعده ۸: زاویه ورود به صفر مختلط برابر با 180 درجه بهاضافه مجموع زوایای بین و همه صفرها منهای مجموع زوایای بین و همه قطبها است:
قاعده ۹: محل برخورد مکان با محور موهومی
واضح است که بهازای برخی مقادیر K، سیستم ناپایدار بوده و مکان ریشهها از محور موهومی عبور خواهد کرد. با روشی مانند راث-هرویتز میتوان محل تقاطع مکان با محور موهومی را بهدست آورد (یعنی فرکانسی که در آن، سیستم ناپایدار میشود).
قاعده 9: با استفاده از قانون راث-هرویتز میتوان محل برخورد مکان ریشهها را با محور موهومی تعیین کرد.
تعیین قطبها با داشتن بهره K
معادله مشخصه را مجدداً به خاطر بیاورید:
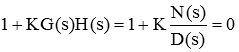
یا
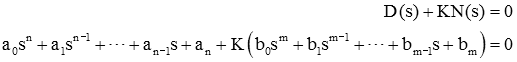
مقادیر و معلوم هستند. برای مقدار داده شده K، میتوان چندجملهای را تعیین و از آن فاکتورگیری کرد و در نتیجه ریشههای معادله مشخصه را بهدست آورد.
با نوشتن معادله مشخصه و قرار دادن K در این معادله، میتوان ریشههای آن را بهدست آورد.
تعیین مقدار K با داشتن قطبها
با استفاده از معادله مشخصه، میتوان مقدار K را بهصورت زیر نوشت:
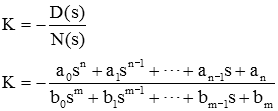
بنابراین، با داشتن مقدار s، میتوان K را بهدست آورد.
اگر s با استفاده از نمودار مکان ریشهها بهدست آمده باشد، تقریبی است. اگر مقدار انتخاب شده، روی مکان ریشهها نباشد، مقدار K بهدست آمده ممکن است مختلط باشد. در این صورت، بخش موهومی کوچک خواهد بود، بنابراین، فقط بخش حقیقی K را در نظر میگیریم. میتوان از این مقدار K برای یافتن مقدار دقیق محل ریشه استفاده کرد.
با نوشتن معادله مشخصه بهصورت ، و جایگذاری s در آن، میتوان مقدار K را محاسبه کرد.
مثال
میخواهیم برای سیستمی با تابع تبدیل حلقه باز زیر، نمودار مکان هندسی ریشهها را رسم کنیم.
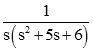
اطلاعات سیستم
تابع تبدیل حلقه باز ، قطب در ، همچنین تعداد صفر محدود (غیر بینهایت) دارد. بنابراین، صفر در بینهایت و ().
میتوان تابع تبدیل حلقه باز را بهصورت نوشت که در آن، چندجملهای صورت و چندجملهای مخرج است. بنابراین، و .
معادله مشخصه برابر است با یا
شکل کامل مکان ریشهها بهصورت زیر است:
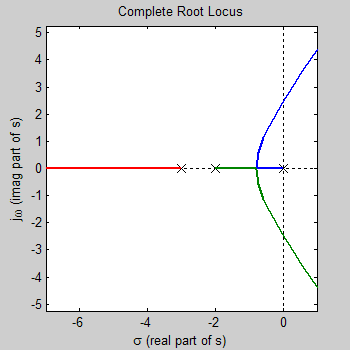
تقارن
همانگونه که از شکل بالا مشخص است، مکان ریشهها نسبت به محور حقیقی، متقارن است.
تعداد شاخهها
تابع تبدیل حلقه باز ، سه قطب دارد، بنابراین، مکان هندسی سه شاخه خواهد داشت. هریک از شاخهها با یک رنگ مجزا نشان داده شده است.
نقاط ابتدا و انتها
مکان ریشهها از قطبهای تابع تبدیل حلقه باز شروع میشود (). این قطبها در شکل فوق با علامت نشان داده شدهاند. وقتی ، محل قطبهای حلقه بسته به صفرهای تابع تبدیل حلقه باز میرسد. البته بهیاد داریم که سه صفر در بینهایت وجود دارد.
مکان روی محور حقیقی
مکان ریشهها روی محور حقیقی، در جایی واقع میشود که سمت راست آن، تعداد فردی صفر و قطب روی محور وجود داشته باشد. بنابراین، مکان ریشهها روی محور حقیقی، بین و 0 و همچنین بین و است.
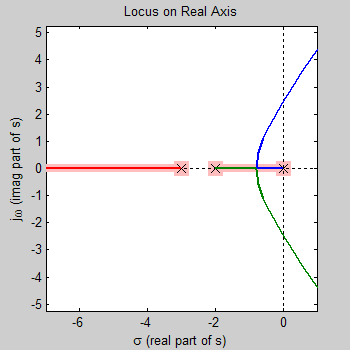
مجانبها
با توجه به وجود سه قطب و یک صفر محدود، زاویه مجانبها ضریب فردی از است (یعنی و ). مجموع قطبها برابر با و مجموع صفرها نیز 0 است.
تقاطع مجانبها بهصورت زیر محاسبه میشود:
((مجموع صفرها)-(مجموع قطبها))
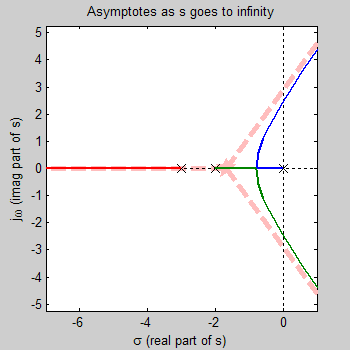
نقاط شکست روی محور حقیقی
نقاط شکست از معادله یا بهدست میآید. این چندجملهای، دو ریشه دارد. این دو نقطه با مربع و لوزی در شکل زیر نشان داده شدهاند.
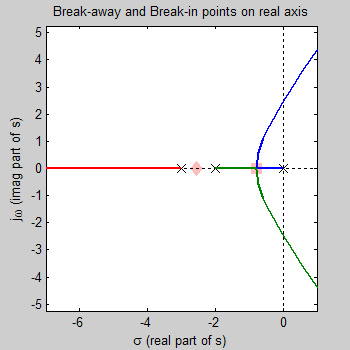
هردوی این ریشهها روی مکان نیستند. از این دو ریشه، روی مکان ریشهها قرار دارد (زیرا ).
زاویه خروج از قطب
تابع تبدیل حلقه باز، قطب مختلط ندارد، بنابراین، زاویه خروج وجود نخواهد داشت.
زاویه ورود به صفر
تابع تبدیل حلقه باز، صفر مختلط ندارد، بنابراین، زاویه ورود وجود نخواهد داشت.
تقاطع با محور موهومی
مکان، محور موهومی را در دو نقطه و بهازای دو مقدار K قطع میکند. این مقادیر را میتوان با استفاده از روش راث-هرویتز تعیین کرد. اگر این کار را انجام دهیم، بهترتیب برای نقاط و بهدست خواهد آمد. شکل زیر، این نقاط را نشان میدهد.
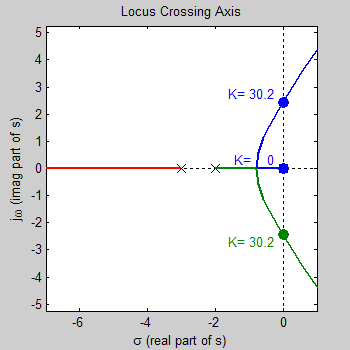
تغییر قطبهای حلقه بسته با تغییر K
با انتخاب K میتوان معادله مشخصه را تعیین کرد که ریشههای آن، قطبهای حلقه بسته هستند. برای مثال، با ، معادله مشخصه یا است. این معادله، 3 ریشه در دارد. این ریشهها، با نقاط توپر در شکل زیر نشان داده شدهاند.
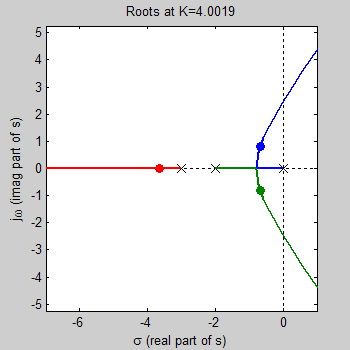
انتخاب قطب و یافتن K
با انتخاب یک مقدار برای قطبها روی مکان هندسی، میتوان مقدار K متناظر با آن را پیدا کرد ().
برای مثال، قطب را انتخاب میکنیم. در نتیجه، و و . این مقدار، دقیقاً روی مکان ریشه نیست، بنابراین K مختلط است و مقدار حقیقی آن () را انتخاب میکنیم.
برای این مقدار K، سه قطب حلقه بسته در وجود دارد.
نکته: اغلب، انتخاب مقدار s بهصورت دقیق روی مکان ریشهها دشوار است، اما میتوان نقطهای را نزدیک آن انتخاب کرد. اگر مقدار دقیقاً روی مکان ریشه نباشد، مقدار K بهجای آنکه حقیقی باشد، مختلط خواهد بود. در این حالت، قسمت موهومی K را که کوچک است، در نظر نمیگیریم. لازم به ذکر است که در این مثال، یک قطب را انتخاب و از روی آن مقدار K را تعیین کردیم. اگر سیستم بیش از یک قطب حلقه بسته داشته باشد، محل قطبهای دیگر نیز با K تعیین میشود و ممکن است در محلهای غیرمطلوبی قرار گیرند.
اگر مطلب بالا برای شما مفید بوده و علاقهمند به موضوعات مرتبط با آن هستید، پیشنهاد میکنیم آموزشهای زیر را نیز مطالعه کنید:
^^


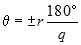
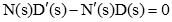
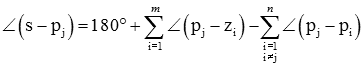











خیلی عالی بود ممنون از آموزش عالیتون🙏🏻 فقط اگر مثال های بیشتری هم حل بکنید خیلی بهتر هم میشود
با عرض سلام خسته نباشید. فقط میتوانم بگویم درود به شرفتان. با ابزار های جدید، آموزش وسیع و عمیقی ارائه دادید به طوری که بدون حضور استاد میتوان درک کاملی از مطلب داشت. امیدواریم روز به روز بر کیفیت کار خود بیافزائید تا هم موجب موفقیت خود و هم باعث آموزش بهتر ما شوید. بسیار سپاسگزارم
خلاصه و بسیار مفید ممنون. 🌹
بسیار عالی اقای زندی
دمت گرمممم
اگر یکم از حالت کتابی صحبت کردن به حالت ارتباط نزدیکی با بیننده برقرار بشه عالی میشه.
اموزش عالی بود .
اتفاقا فن بیان صریح و واضح و بدون معطلی ممنونم واقعا
واقعا ممنون از توضیحات فوق العادتون.میشه کامل و از 0 همه چی رو یاد گرفت با اموزشتون
چقدر با سواد کامل توضیح داده شده
سلام حسین عزیز.
از پیام محبتآمیزتان بسیار خوشحالیم.
سالم و سربلند باشید.
بسیار بسیار عالی بود خسته نباشد
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
سالم و سربلند باشید.
خیلی عالی و کامل بود.
سلام وقت بخیر استاد آموزشتون خیلی عالی و واضح بود سپاس فراوان?
بسیار آموزنده، کامل و عالی!