مقدمهای بر حساب – راهنمای شهودی به زبان ساده


حساب بخشی از ریاضیات است که برای دستکاری و تبدیل اعداد استفاده میشود. این تبدیلها کارآمد هستند و در برخی موارد چیزهایی در جهان واقعی وجود دارند که میخواهیم به همین ترتیب مورد تبدیل قرار دهیم. اما سوالی که وجود دارد این است که چرا حساب مهم است؟
اگر حساب را به عنوان نوعی تبدیل ببینیم که باعث میشود مفاهیم به ظاهر عجیب، برای مثال جذر 1- معنی پیدا کنند، میتوانیم مسائل را نیز به همین ترتیب به صورت بصری درک کنیم.
جمع
جمع ساده است، با این حال چند حالت دارد:
- تجمیع: شمارش کمیتهای مشابه در کنار هم (در اغلب اوقات برای موارد ملموس)
- جابجایی: شیفت کردن یک عدد در راستای یک محور (برای چیزهای کمتر ملموس مانند دما)
- ترکیب: ایجاد یک کمیت جدید از دو کمیت متفاوت (مانند نتهایی در یک آکورد موسیقی)

اما معنی دقیق جمع چیست؟ همه چیز به چارچوب مسئله بستگی دارد. زمانی که سیبها را جمع میکنیم، مشغول گردآوری آیتمهای مشابه هستیم (3 سیب + 4 سیب = 7 سیب). وقتی دما را اندازهگیری میکنیم (حرارتی را که در راستای یک محور قرار دارد با هم جمع میزنیم (3 درجه + 4 درجه = 7 درجه)
زمانی که بردارها را جمع میکنیم، استفاده از کلمه ترکیب معنیدارتر است: (3 بلوک به سمت شرق + 4 بلوک به سمت شمال = 5 بلوک در سمت جدید.) در این حالت باید اجزای مؤلفهای را ردگیری کنیم و بین شمال و شرق تفاوت قائل باشیم. زمانی که مشغول جمع زدن سیبها هستیم، میتوانیم همه آیتمها را کنار هم قرار دهیم و دیگر لازم نیست نگران باشیم که آنها زمانی به صورت 3 و 4 آیتم بودند.
یک عملیات منفرد (جمع) میتواند چندین معنی شهودی متفاوت داشته باشد. البته این فهرست جامع نیست و شما نیز میتوانید موارد دیگری را به آن اضافه کنید.
ضرب
ضرب را نیز میتوان به چند روش تفسیر کرد:
- تکرار: اجرای چندین جمع
- مقیاس بندی: بزرگتر یا کوچکتر کردن یک عدد به یکباره
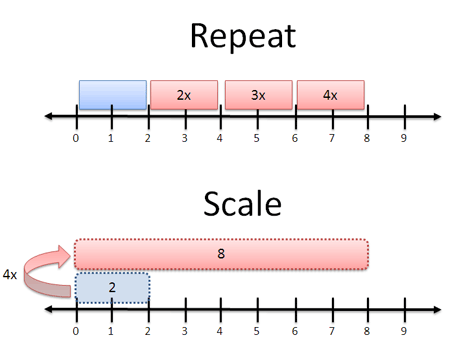
معنایی که ما تفسیر میکنیم به چارچوب مسئله بستگی دارد. در مورد سیب منظور از «4x» یعنی تعداد 2 سیب را به 8 سیب افزایش دهیم (چهار گروه 2 تایی) در مورد نرمافزار عکس، «4x» به معنی این است که یک تصویر 2 اینچی را به تصویری 8 اینچی تبدیل کنیم. هر کدام از این معانی متفاوت هستند. برای مثال اگر در این موارد یک سیب بزرگ دو کیلویی یا 4 تصویر جداگانه دریافت کنید، چندان خوشحال نخواهید شد.
ضرب در یک معنی ظریفتر به معنی «تکرار جمع» است. اما این تفسیر همواره سادهترین تفسیر نیست. برای نمونه آیا میتوانید «تکرار جمعی» به میزان 7.3 بار را تصور کنید؟
منفی و معکوس
وضعیتهای منفی و معکوس اعداد، نشان دهنده ایده «متضاد» یا «مقابل» هستند. اما این توصیفها مبهم هستند. منظور از متضاد ضرب در دو چیست؟
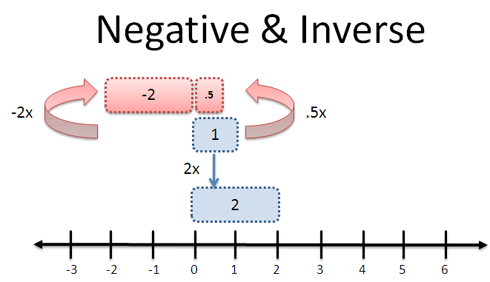
«متضاد» میتواند به چندین معنی باشد:
- ضرب در 1/2: یعنی یک سود به مقدار 1 را تبدیل به سود 1/2 کنیم (یعنی آن را کاهش دهیم).
- ضرب در 2-: یعنی سود به مقدار 2 را به ضرری برابر با 2 تبدیل کنیم (معکوس کنیم).
با این حال در این مورد نیز چارچوب مسئله است که معنا را تعیین میکند. زمانی که یک شرکت «سودی را معکوس میکند»، یعنی آن را به ضرر تبدیل کرده است، یعنی ضرب در عدد منفی. زمانی که یک مقدار بزرگنمایی را در یک نرمافزار تصویر معکوس میکنیم، میخواهیم تصویر را کوچکتر کنیم (نه این که آن را بازتاب دهیم) بنابراین آن را در 1/2 ضرب میکنیم. در نهایت دوباره تأکید میکنیم که تنها چارچوب مسئله است که میتواند تفسیر ما را از عملیات حسابی مشخص کند.
معادله چیست؟
معادله همان سؤال است. برای مثال عبارت زیر را ببینید:
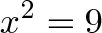
این چیزی بیش از یک مسئله ساده است. معادله را باید به صورت زیر در نظر گرفت:

چه تبدیلی (ضرب x) است که وقتی دو بار اعمال شود، 1 را به توان 9 میرساند؟
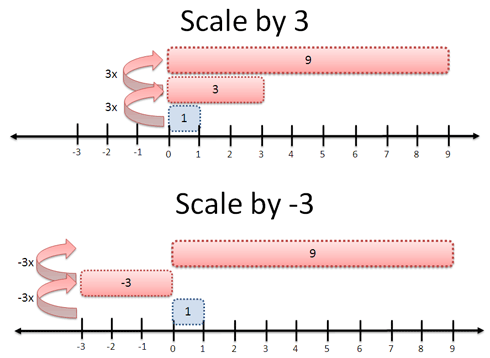
برای سؤال فوق دو پاسخ داریم:
- مقیاس 3: یعنی اگر 3 را دو بار در هم ضرب کنیم به عدد 9 میرسیم:
1 * 3 * 3 = 9
- مقیاس 3 و معکوس (3-) یعنی دو بار در 3 ضرب کنیم تا به 9 برسیم
1 * -3 * -3 = 9.
در توضیح فوق از عدد 1 استفاده کردیم تا به شما نشان دهیم که چه چیزی مورد تبدیل قرار میگیرد. البته این وضعیت اختیاری است؛ اما این چیزی نیست که در مورد آن تا کنون فکر کرده باشیم.
اگر در این مسیر چند گام به عقب بازگردیم، میتوانیم ببینیم که حساب روشی برای بزرگ، کوچک، معکوس و یا بر عکس کردن اعداد به صورت عددهای دیگر است. ما توانستیم یک تبدیل بزرگ (9) را به دو تبدیل کوچکتر (3 یا 3-) درآوریم.
مثالهایی از دنیای واقعی: اعداد تصادفی
نظریهپردازی کافی است و در این بخش میخواهیم این پیشزمینه ذهنی را در عمل به شما نشان دهیم. اغلب زبانهای برنامهنویسی یک تابع ()random دارند که عددی بین 0 تا 1 ارائه میکند. اما اگر ما عددی بین 5 تا 10 بخواهیم باید چه کار کنیم؟ سؤال به این شکل است که چگونه میتوان محدوده 0 تا 1 را به محدوده 5 تا 10 تبدیل کرد؟

عملیاتهای حسابی در اینجا به کمک میآیند.
- ابتدا محدوده 1-0 را با ضرب کردن در 5 به صورت 5-0 در میآوریم
- سپس با افزودن 5 محدوده 5-0 را به محدوده 10-5 جابجا میکنیم
- و در نهایت محدودهای به صورت 10-5 داریم.
در هر صورت، این محدوده میتواند برای مثال محدوده سنی بین 56-18 باشد یا سالهای 2007-1960 را شامل شود یا دماهای بین 5- تا 40 درجه را در یک شبیهسازی در برگیرد. مهم نیست که محدوده شما چقدر است، می تونید از محدوده 0 تا 1 برای ساختن بازه مورد نظر استفاده کنید.
سخن پایانی
در این نوشته ایده این که حساب همان تبدیل است را بررسی کردیم. شما اعدادی را به صورت عددهای دیگر در میآورید و هر تبدیل یک معنایی دارد. برخی از آنها برای یک موقعیت مناسبتر از انواع دیگر هستند.
هدف از این نوشته این نیست که عملیات ضرب را به صورت یک فرایند نمایش نمودارهای پیچیده تبدیل کنیم. بلکه تلاش کردهایم تا با استفاده از این تکنیک، ذهنیتی در اختیار شما قرار دهیم تا از آن همانند سلاحی برای مبارزه با عملیاتهای به ظاهر پیچیده استفاده کنید.
وقتی مشغول مطالعه جبر خطی (ماتریسها) هستید میتوانید ضرب را به صورت یک نوع تبدیل (مقیاسبندی، چرخش، اریب ساختن) به جای یک مجموعه عملیاتهایی که روی ماتریس اعمال شوند در نظر بگیرید. این رویکرد زمانی که مشغول بررسی اعداد موهومی هستید، بسیار مفید خواهد بود. بینشهای کوچک، ایدههای بزرگی را به بار میآورند.
اگر به مطالعه این نوشته علاقهمند بودهاید، احتمالاً موارد زیر نیز مورد توجه شما قرار خواهند گرفت:
- آموزش ریاضی پایه دانشگاهی
- آموزش ریاضیات عمومی ۱
- مجموعه آموزشهای ریاضیات
- مجموعه ها در ریاضیات – مفاهیم پایه
- آموزش محاسبات سریع ریاضی
- آموزش های رایگان ریاضی و فیزیک
==













سلام ممنون بابت تمام محتواهای بارزشی که ایجاد کردید یه دنیا سپاس خیلی دید بهتری به ریاضی دارم اگر امکانش هست در خصوص ضرب علامت منفی در منفی چه درکی میشه از اون داشت اگر بشه یه توضیحی در خصوصش بدید ممنون میشم