نسبت پواسون و رفتار مواد در محدوده الاستیک – به زبان ساده
بسیاری مواد مورد استفاده در سازهها از قبیل فلزات، چوب، پلاستیکها و سرامیکها در ابتدای فرآیند بارگذاری به صورت الاستیک و خطی رفتار میکنند. این مسئله باعث شکلگیری یک خط مستقیم در ابتدای منحنی تنش-کرنش این مواد میشود. در این مقاله، برای آشنایی بیشتر با رفتار مواد در محدوده الاستیک، به توضیح مفاهیم الاستیک خطی، قانون هوک و نسبت پواسون خواهیم پرداخت. در انتها نیز علاوه بر تشریح یک مسئله کاربردی، جدول مقادیر نسبت پواسون برای برخی از مواد پرکاربرد مهندسی را برای شما ارائه خواهیم کرد.
مواد الاستیک خطی
شکلهای زیر، به ترتیب منحنیهای تنش-کرنش فولاد سازهای، یک نوع آلیاژ آلومینیوم، یک ماده شکننده و مس را نمایش میدهند. همان طور که مشاهده میشود، در ابتدای منحنی و از نقطه O تا حد تناسب (نقطه A در برخی از منحنیها)، ماده هم به صورت الاستیک و هم به صورت خطی رفتار میکند.
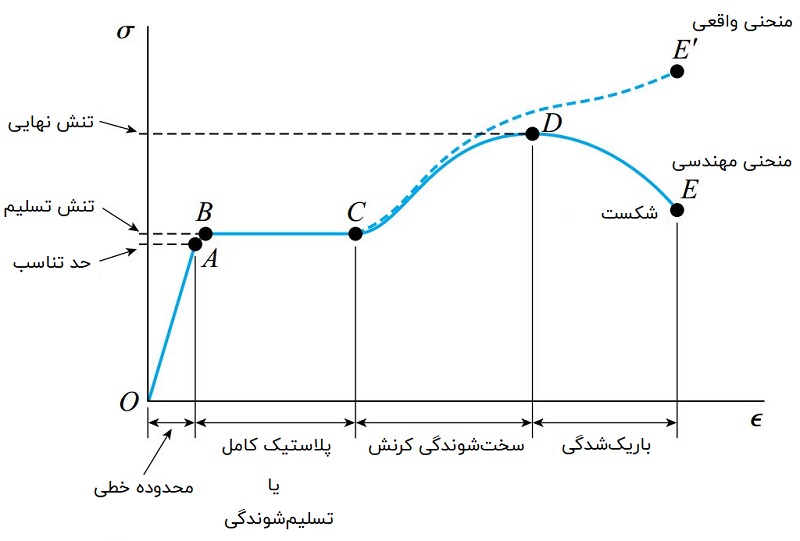
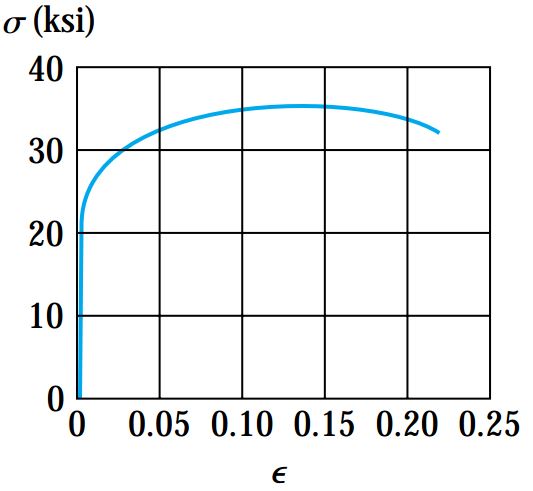
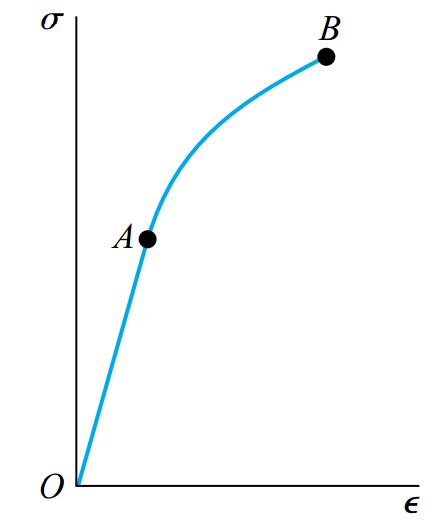
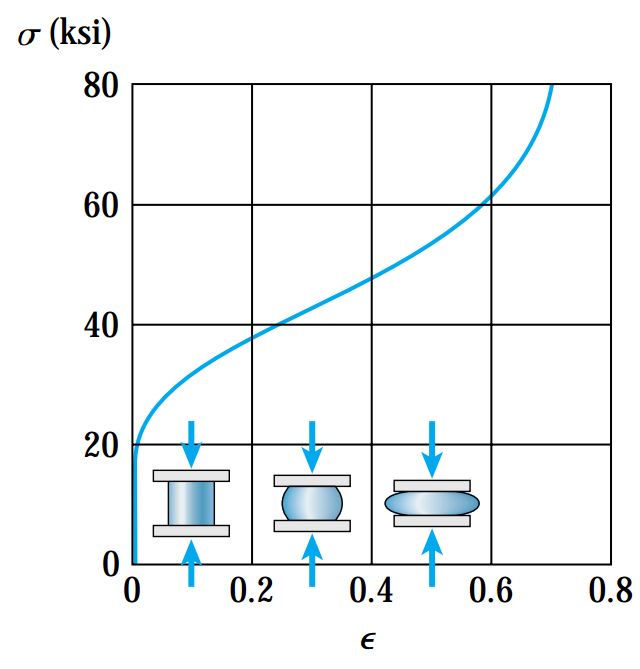
به موادی که به صورت الاستیک رفتار میکنند و رابطه بین تنش و کرنش آنها خطی است، مواد «الاستیک خطی» (Linearly Elastic) گفته میشود.
مطالعه این رفتار از اهمیت بسیار بالایی در مسائل مهندسی برخوردار است. اگر سازهها و دستگاههای مختلف به منظور عملکرد در ناحیه الاستیک خطی طراحی شوند، از ایجاد تغییر شکلهای دائمی ناشی از تسلیم ماده جلوگیری میشود.
قانون هوک
رابطه خطی بین تنش و کرنش برای یک میله ساده تحت فشار یا کشش از طریق معادله زیر بیان میشود:

σ: تنش محوری؛ ε: کرنش محوری؛ E: ثابت تناسب که با عنوان «مدول الاستیسیته» (Elasticity Modulus) ماده شناخته میشود.
مدول الاستیسیته، شیب منحنی تنش-کرنش در بخش الاستیک خطی را نمایش میدهد. از آنجایی که کرنش یک پارامتر بدون بعد به شمار میرود، واحد مدول الاستیسیته با واحد تنش یکسان است. این مدول در سیستم آمریکایی با واحد پوند بر اینچ مربع (psi) یا کیلو پوند بر اینچ مربع (ksi) و در سیستم SI با واحد پاسکال (Pa) یا مگاپاسکال (MPa) نمایش داده میشود.
رابطه σ=Eε با عنوان «قانون هوک» (Hooke’s Law) شناخته میشود. این عنوان از نام دانشمند معروف انگلیسی، «رابرت هوک» (Robert Hooke) گرفته شده است. هوک اولین دانشمندی بود که به طور گسترده بر روی خواص الاستیک مواد تحقیق کرد و آزمایشهای متعددی را بر روی مواد مختلفی نظیر فلز، چوب، سنگ، استخوان و غیره انجام داد. او با اندازهگیری میزان کشیدگی در سیمهای متصل به وزنه دریافت که بین میزان تغییرات طول سیم و وزنههای به وجود آورنده این تغییرات همیشه یک تناسب ثابت وجود دارد. به این ترتیب، هوک بین بارهای اعمال شده و کشیدگیهای به وجود آمده یک رابطه خطی ایجاد کرد.
رابطه σ=Eε، یک فرم بسیار ساده از قانون هوک را به نمایش میگذارد. این رابطه تنها برای تنش و کرنشهای طولی موجود در یک میله تحت فشار یا کشش کاربرد دارد. اگرچه، حالت تنش اکثر سازهها و دستگاهها پیچیده است و برای آنها باید از معادلات تعمیمیافته قانون هوک استفاده کرد. به عنوان مثال، قانون هوک در شرایط تنش و کنرش برشی را نمایش میدهد.
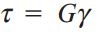
?: تنش برشی؛ G: مدول برشی الاستیسیته یا مدول صلبیت؛ γ: کرنش برشی
مواد بسیار سخت (مانند فولاد سازهای)، مدول الاستیسیته نسبتاً بزرگی دارند. مقدار این مدول برای فولاد در حدود 210 گیگاپاسکال و برای آلومینیوم در حدود 73 گیگاپاسکال است. در طرف مقابل، مواد انعطافپذیر، مدول الاستیسیته کمتری دارند. مقدار این مدول برای پلاستیکها معمولاً در محدودهای بین 0.7 گیگاپاسکال تا 14 گیگاپاسکال قرار میگیرد.
مدول الاستیسیته با عنوان «مدول یانگ» (Young’s Modulus) نیز شناخته میشود. این عنوان از نام دانشمند انگلیسی، «توماس یانگ» (Thomas Young) گرفته شده است. یانگ ایده مدول الاستیسیته را در حین تحقیق بر روی میلههای تحت کشش و فشار ارائه کرد. مدول یانگ با مدول الاستیسیته امروزی متفاوت است. در مدول ارائه شده توسط یانگ، ویژگیهای هندسی میله و همچنین خصوصیات ماده تشکیلدهنده آن نیز در نظر گرفته میشد.
نسبت پواسون
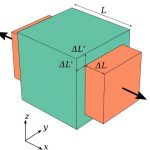
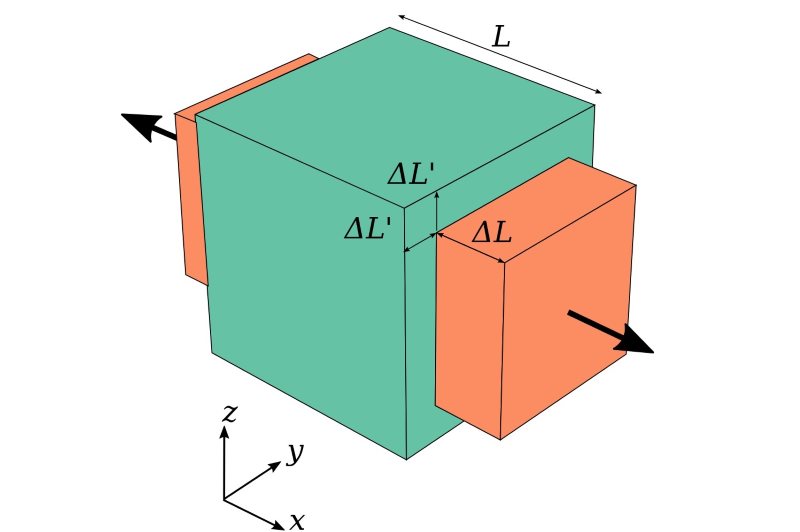
هنگامی که یک میله منشوری تحت کشش قرار میگیرد، افزایش طول آن با انقباض جانبی همراه میشود. در شکل زیر، وضعیت یک میله منشوری پیش از بارگذاری و تغییر شکل های به وجود آمده در آن پس از بارگذاری نمایش داده شده است.
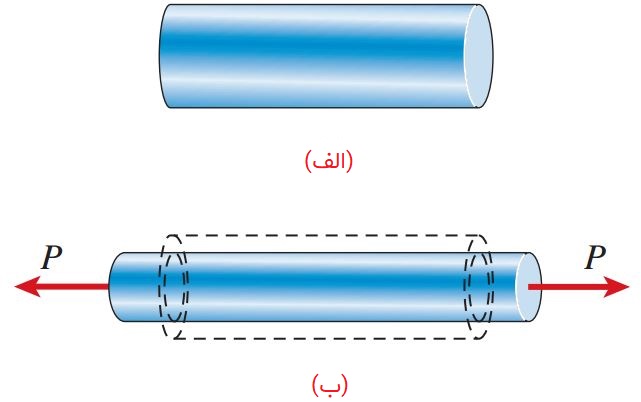
انقباض جانبی را میتوان به وضوح در نوارهای لاستیکی تحت کشش مشاهده کرد. با این وجود، تغییر شکلهای جانبی مواد فلزی در ناحیه الاستیک خطی معمولاً بسیار کوچک و غیر قابل تشخیص هستند. اگرچه، این تغییر شکلها را میتوان با استفاده از وسایل اندازهگیری حساس تشخیص داد.
اگر ماده تشکیلدهنده یک میله دارای خاصیت الاستیک خطی باشد، کرنش جانبی ('ε) در هر نقطه از میله با کرنش محوری (ε) آن در همان نقطه متناسب خواهد بود. نسبت این دو کرنش، یکی از خواص ماده را نمایش میدهد. این خاصیت، «نسبت پواسون» (Poisson’s Ratio) نام دارد. نسبت پواسون، یک پارامتر بدون بعد است که معمولاً با حرف یونانی نو (ν) نمایش داده میشود. این نسبت از طریق رابطه زیر به دست میآید:

علامت کرنشهای محوری و جانبی مخالف یکدیگر است. بنابراین، برای تبدیل نسبت پواسون به یک مقدار مثبت از یک علامت منفی در رابطه آن استفاده میشود. به عنوان مثال، در یک میله تحت کشش علامت کرنش محوری مثبت و علامت کرنش جانبی آن (به دلیل کاهش عرض میله) منفی است. برای یک میله تحت فشار، طول میله کاهش و عرض آن افزایش مییابد. به همین دلیل، علامت کرنش محوری منفی و علامت کرنش جانبی مثبت خواهد بود. در صورت مشخص بودن نسبت پواسون یک ماده میتوان مقدار کرنش جانبی آن را با استفاده از کرنش محوری به دست آورد:
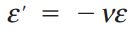
عنوان نسبت پواسون از نام ریاضیدان مشهور فرانسوی، «سیمون دنیس پواسون» (Simeon Denis Poisson) گرفته شده است. پواسون تلاش کرد که این نسبت را با استفاده از تئوری مولکولی مواد محاسبه کند. بر اساس این محاسبات، او به نسبت ν=1/4 برای مواد همسانگرد دست یافت. در مطالعات اخیر که طبق مدلهای مبتنی بر ساختار اتمی مواد صورت گرفتهاند، نسبت ν=1/3 برای مواد همسانگرد به دست آمده است. مقدار ضریب پواسون برای اکثر فلزات و بسیاری از مواد دیگر، عددی بین 0.25 تا 0.35 است. چوبپنبه جز موادی به شمار میرود که نسبت پواسون آن بسیار کوچک و عملاً صفر است. این نسبت برای بتن حدود 0.1 تا 0.2 است. حد بالایی نسبت پواسون از نظر تئوری 0.5 در نظر گرفته میشود. نسبت پواسون مواد لاستیکی به این مقدار نزدیک است.
هنگامی که کرنش درون یک ماده بزرگ میشود، نسبت پواسون آن تغییر میکند. به عنوان مثال، هنگام رخ دادن تسلیم پلاستیک در فولاد سازهای، مقدار نسبت پواسون آن به حدود 0.5 میرسد. بنابراین، نسبت پواسون تنها در محدوده الاستیک خطی ثابت است. اگر رفتار مادهای غیر خطی باشد، به نسبت کرنش جانبی به کرنش محوری آن «نسبت انقباض» (Contraction Ratio) گفته میشود. در مورد رفتار الاستیک خطی، نسبت انقباض با نسبت پواسون برابر است.
در هنگام استفاده از روابط نسبت پواسون باید توجه داشت که این روابط تنها برای میلههای تحت تنش تکمحوری قابل استفاده هستند. در تنش تکمحوری، تنها تنش نرمال σ در راستای محور میله اعمال میشود.
شرایط محاسبه نسبت پواسون
برای یک ماده بخصوص، نسبت پواسون در محدوده الاستیک خطی ثابت باقی میماند. بنابراین با افزایش یا کاهش بارگذاری، میزان کرنش جانبی در هر نقطه از یک میله منشوری متناسب با کرنش محوری آن تغییر میکند. با این وجود، به منظور ثابت بودن کرنشهای جانبی در سراسر میله هنگام اعمالِ یک بار مشخص باید شرایط دیگری نیز برقرار باشد. 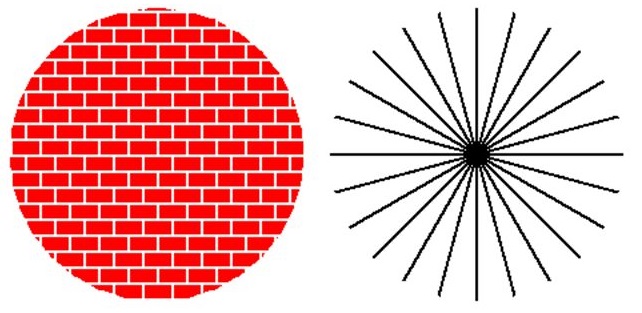
نمای شماتیک خاصیت همسانگردی (سمت راست) و خاصیت همگنی (سمت چپ)شرایط محاسبه نسبت پواسون عبارت هستند از:
- شرط اول برای یکنواخت بودن کرنش جانبی در سراسر میله، همگن بودن ماده است. به این منظور باید مواد تشکیلدهنده میله در تمام نقاط دارای ترکیبات یکسان و در نتیجه خواص الاستیک مشابه باشند. اگرچه، همگن بودن ماده در تمامی نقاط به معنای یکسان بودن خواص الاستیک آن در تمام جهات نیست. به عنوان مثال، مدول الاستیسیته موادی نظیر چوب در راستای جانبی با مدول الاستیسیته آن در راستای محوری تفاوت دارد. به همین دلیل به سراغ شرط دوم میرویم.
- شرط دوم برای یکنواخت بودن کرنش جانبی در سراسر میله، یکسان بودن خواص الاستیک مواد در راستای عمود بر محور طولی است. شرایط بالا برای اکثر مواد فلزی صدق میکند. به همین دلیل، کرنشهای جانبی در میلههای فلزی تحت بارگذاری یکنواخت کششی در تمام نقاط میله یکسان خواهند بود. به علاوه، این کرنشها در تمام جهات مقدار برابری خواهند داشت.
به موادی خواص آنها در تمام جهات (محور، جانبی و جهات دیگر) یکسان است، «همسانگرد» (Isotropic) گفته میشود. اگر خواص مادهای در جهات مختلف تغییر کند، آن ماده «ناهمسانگرد» (Anisotropic) خواهد بود.
حل یک مثال کاربردی
یک لوله فولادی با طول 4 فوت (L)، قطر خارجی 6 اینچ (d2) و قطر داخلی 4.5 اینچ (d1) در اثر اعمال نیروی محوری 140 کیلو پوند (P) تحت فشار قرار گرفته است (شکل زیر). مدول الاستیسیته این فولاد برابر 30000 کیلو پوند بر اینچ مربع، نسبت پواسون آن 0.30 و تنش تسلیم آن 50 کیلو پوند بر اینچ مربع است.
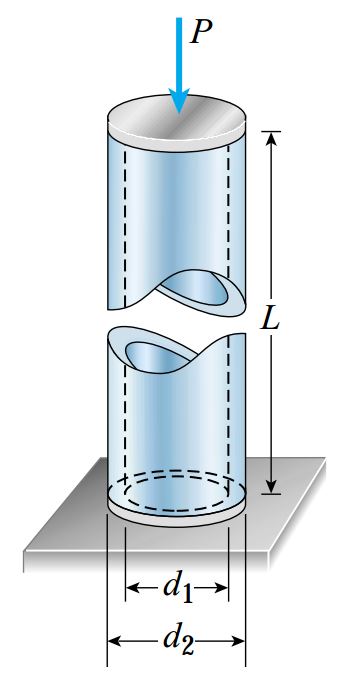
با توجه به اطلاعات مسئله، میزان کاهش طول (δ)، کرنش جانبی ('ε)، میزان افزایش قطر خارجی (Δd2)، میزان افزایش قطر داخلی (Δd1) و میزان افزایش ضخامت دیواره لوله (Δt) را محاسبه کنید.
مساحت سطح مقطع (A) و تنش طولی (σ) به صورت زیر محاسبه میشود:


علامت منفی تنش نشان دهنده فشاری بودن بار اعمالشده است. به دلیل کوچکتر بودن تنش از تنش تسلیم، ماده در محدوده الاستیک خطی رفتار خواهد کرد. میزان کرنش محوری میله از قانون هوک به دست میآید:
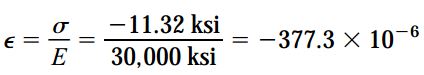
علامت منفی این کرنش، بیانگر کوتاه شدن طول لوله است.
اکنون با مشخص شدن کرنش محوری میتوانیم تغییرات طول لوله را محاسبه کنیم:

علامت منفی این تغییرات، به کوتاه شدن طول لوله اشاره دارد.
به این ترتیب، کرنش جانبی از رابطه نسبت پواسون قابل تعیین خواهد بود:
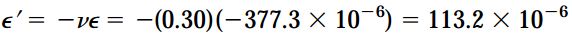
علامت مثبت کرنش جانبی 'ε، افزایش ابعاد جانبی لوله را نشان میدهد (تأثیر بارگذاری فشاری).
میزان افزایش قطر خارجی از ضرب کرنش جانبی در قطر به دست میآید:
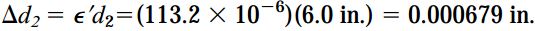
میزان افزایش قطر داخلی نیز به روش مشابه تعیین میشود:

میزان افزایش ضخامت دیواره لوله نیز از همین روش استفاده میکنیم:

برای اطمینان از صحت میزان افزایش محاسبه شده برای دیواره لوله، اختلاف تغییرات قطر خارجی با تغییرات قطر داخلی را تقسیم بر دو میکنیم:
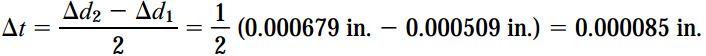
همانگونه که مشاهده میکنید، دو مقدار به دست آمده با هم برابر هستند.
توجه داشته باشید که در حین اعمال فشار، تمام کمیتها از قبیل قطر خارجی، قطر داخلی و ضخامت دیواره افزایش مییابد.
توجه: مقدار عددی به دست آمده در این مثال نشان میدهند که تغییرات ابعاد مواد سازهای در شرایط بارگذاری نرمال بسیار کوچک هستند. علیرغم کوچک بودن این مقادیر، در تحلیلهای بخصوص و در روشهای تجربیِ تعیین تنش و کرنش، تغییرات ابعاد میتوانند اهمیت بالایی داشته باشند.
مقادیر نسبت پواسون برای برخی از مواد پرکاربرد مهندسی
در جدول زیر، نسبت پواسون مواد مختلف نمایش داده شده است. در بسیاری از مواد، میزان نسبت پواسون برای بارگذاری کششی و فشاری برابر در نظر گرفته میشود.
| ماده | نسبت پواسون |
| آلیاژهای آلومینیوم
2014-T6 6061-T6 7075-T6 | 0.33
0.33 0.33 0.33 |
| برنج | 0.34 |
| برنز | 0.34 |
| آهن ریختهگری | 0.2-0.3 |
| بتن (تحت فشار) | 0.1-0.2 |
| مس و آلیاژهای مس | 0.33-0.36 |
| شیشه | 0.17-0.27 |
| آلیاژهای منیزیوم | 0.35 |
| مونل (70 درصد نیکل و 30 درصد مس) | 0.32 |
| نیکل | 0.31 |
| پلاستیک
نایلون پلیاتیلن | -
0.4 0.4 |
| سنگ (تحت فشار)
گرانیت، مرمر، کوارتز سنگ آهک، ماسه سنگ | -
0.2-0.3 0.2-0.3 |
| لاستیک | 0.45-0.50 |
| فولاد | 0.27-0.30 |
| آلیاژهای تیتانیوم | 0.33 |
| تنگستن | 0.2 |
^^













باعرض سلام
چرانسبت پواسون در ناحیه پلاستیک 0/5 می باشد
میتوان اثبات کرد