کرنش صفحه ای (Plane Strain) و معادلات تبدیل آن – آموزش جامع
«کرنش صفحهای» (Plane Strain)، حالتی است که در آن تمام مؤلفههای کرنش درون یک صفحه قرار میگیرند. این نوع کرنش هنگامی رخ میدهد که یکی از سه مؤلفه اصلی کرنش در المان مورد تحلیل برابر با صفر باشد. در این مقاله، شما را با مفهوم کرنش صفحه ای، تفاوتها و شباهتهای آن با تنش صفحهای، کرنشهای موجود بر روی مقاطع دورانیافته، معادلات تبدیل، نحوه اندازهگیری و حالتهای خاص این نوع کرنش آشنا خواهیم کرد. در انتها نیز به تشریح چند مثال کاربردی خواهیم پرداخت.


معادلات تبدیل کرنشهای صفحهای، کاربرد بسیار گستردهای در تحقیقات آزمایشگاهی و ارزیابی سازهها در هنگام اندازهگیری مقادیر کرنش دارند. کرنشهای به وجود آمده در نمونههای آزمایشگاهی یا عضوهای سازه معمولاً با استفاده «استرین گِیج» (Strain Gauge) یا اصطلاحاً کرنشسنج اندازهگیری میشوند. به عنوان مثال، با قرار دادن کرنشسنج بر روی هواپیما، رفتار بخشهای مختلف آن را در حین پرواز مورد بررسی قرار میگیرد. با نصب کرنشسنج بر روی ساختمانهای مختلف نیز امکان ارزیابی اثرات زلزله بر روی این سازهها فراهم میشود. هر یک از گیجهای کرنشسنج، میزان کرنش در یک جهت خاص را اندازهگیری میکند. از اینرو، به منظور تعیین کرنشهای موجود در جهات دیگر باید از معادلات تبدیل استفاده کرد. در بخشهای مختلف این مقاله، نحوه تعیین معادلات تبدیل کرنشهای صفحهای را برای شما تشریح خواهیم کرد.
مقایسه کرنش صفحهای با تنش صفحهای
در این بخش به تعریف کرنش صفحهای و ارتباط آن با تنش صفحهای میپردازیم. یک المان کوچک با ابعاد b ،a و c در راستای y ،x و z را در نظر بگیرید (شکل زیر).
اگر تغییر شکلهای به وجود آمده در این المان تنها بر روی صفحه xy اعمال شوند، سه مؤلفه کرنش εy ،εx و γxy درون سیستم به وجود میآیند (کرنش نرمال εx در راستای محور x، کرنش نرمال εy در راستای محور y و کرنش برشی γxy در صفحه xy). به این حالت، کرنش صفحهای گفته میشود.
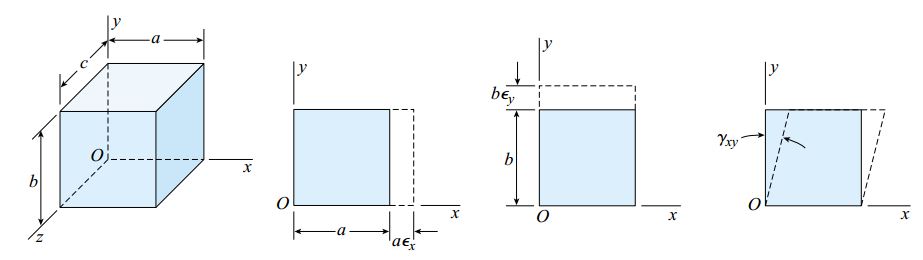
در حالت کرنش صفحهای، کرنش نرمال εz در راستای محور z، کرنش برشی γxz در صفحه xz و کرنش برشی γyz در صفحه yz صفر هستند. به این ترتیب، شرایط زیر برای این حالت در نظر گرفته میشوند:
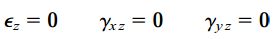
با توجه به تعریف ارائه شده، کرنش صفحهای هنگامی به وجود میآید که صفحات جلویی و پشتی یک المان به طور کامل مهار شده باشند و هیچ جابجایی در راستای z رخ ندهد. در واقعیت چنین وضعیت ایدهآلی به ندرت اتفاق میافتد. با این وجود، این موضوع به معنای عدم کاربرد معادلات تبدیل کرنش صفحهای نیست. بالعکس، این معادلات کاربرد بسیار زیادی در محاسبه کرنشهای موجود در حالت تنش صفحهای دارند. مفهوم کرنش صفحهای مشابه تنش صفحهای است. در تنش صفحهای، مؤلفههای زیر باید دارای مقادیر صفر باشند:
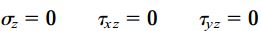
مؤلفههای دیگر نظیر σy ،σx و τxy میتوانند مقادیر غیر صفر داشته باشند. در جدول زیر، مؤلفههای تنش و کرنش در حالت تنش صفحهای و کرنش صفحهای مورد مقایسه قرار گرفتهاند.
| وضعیت المان | تنش صفحهای | کرنش صفحهای |
| تصویر المان | 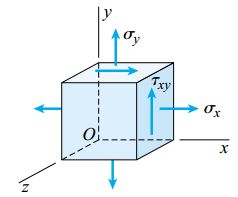 |  |
| مولفههای تنش |  | 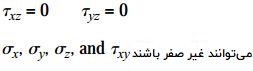 |
| مولفههای کرنش |  |  |
توجه داشته باشید که شباهت بین مفاهیم تنش صفحهای و کرنش صفحهای به معنای رخ دادن همزمان آنها نیست. به طور کلی، المانی که تحت تنش صفحهای قرار دارد، در راستای z نیز تغییر شکل میدهد. در این شرایط، المان تنش لزوماً تحت حالت کرنش صفحهای قرار نخواهد داشت.
این مسئله برای حالت کرنش صفحهای و وجود تنش در راستای z نیز صدق میکند. در دو حالت خاص، تنش صفحهای و کرنش صفحهای به طور همزمان رخ میدهند. در حالت اول، المان باید تحت تنشهای نرمال هماندازه و مختلف العلامت قرار داشته باشد (σx=-σy) و ماده تشکیلدهنده آن باید از قانون هوک پیروی کند. در حالت دوم که یک مورد فرضی است، باید نسبت پواسون ماده تشکیلدهنده المان برابر با صفر باشد (ν=0).
کاربرد معادلات تبدیل
معادلات تبدیل تنش بر روی صفحه xy را میتوان در صورت وجود تنش نرمال σz نیز مورد استفاده قرار داد. دلیل این امر، عدم حضور σz در معادلات تعادل مورد استفاده برای تبدیلات تنش است.
بنابراین، معادلات تبدیل تنش صفحهای برای تنشهای موجود در حالت کرنش صفحهای نیز کاربرد دارند. این معادلات عبارت اند از:
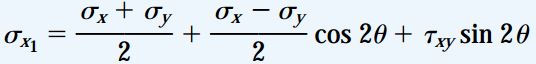
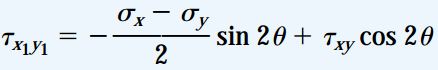
این شرایط برای حالت کرنش صفحهای نیز صدق میکند. به این ترتیب، با تعیین معادلات تبدیل کرنش برای حالت کرنش صفحهای در صفحه xy، این معادلات در صورت وجود کرنش εz نیز قابل استفاده خواهند بود. این موضوع دلیل سادهای دارد. کرنش εz در رابطه هندسی به کار رفته برای تعیین معادلات تبدیل تأثیرگذار نیست.
بنابراین، معادلات تبدیل کرنش صفحهای را میتوان برای کرنشهای موجود در حالت تنش صفحهای نیز به کار برد. در نهایت، باید به خاطر داشته باشید که معادلات تبدیل تنش صفحهای تنها با استفاده از معادلات تعادل به دست میآیند و به همین خاطر برای تمام مواد (الاستیک یا غیر الاستیک) قابل استفاده هستند. معادلات تبدیل کرنش صفحهای نیز همین شرایط را دارند. این معادلات تنها با استفاده از روابط هندسی به دست میآیند و به همین دلیل مستقل از خواص ماده هستند.
مراحل تعیین معادلات تبدیل کرنش صفحهای
به منظور تعیین معادلات تبدیل کرنش صفحهای، از محورهای مختصات نمایش داده شده در شکل زیر کمک میگیریم. در ابتدا فرض میکنیم که مقادیر کرنشهای نرمال εx و εy به همراه کرنش برشی γxy بر روی محورهای xy مشخص هستند.
با استفاده از این مقادیر، روابط مورد نیاز برای تعیین کرنش نرمال εx1 و کرنش برشی γx1y1 بر روی محورهای x1y1 را به دست میآوریم.
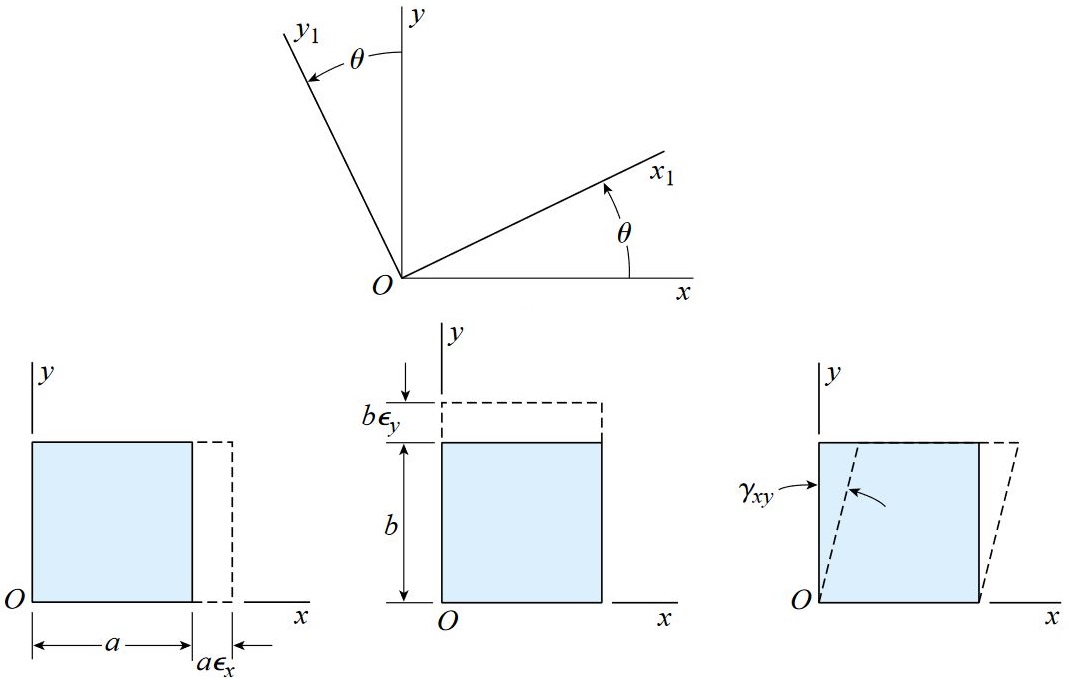
محورهای x1y1 تحت زاویه θ نسبت به محورهای xy و به صورت ساعتگرد دوران یافتهاند. توجه داشته باشید که با جایگذاری θ+90 به جای θ در معادله εx1، معادله جداگانهای برای تعیین کرنش نرمال εy1 به دست میآید.
کرنش نرمال εx1
به منظور تعیین کرنش نرمال εx1 در راستای x1، یک المان کوچک از ماده را مطابق شکل زیر به گونهای در نظر میگیرم که محور x1 بر روی قطر صفحه z و محورهای x و y بر روی اضلاع آن قرار گرفته باشند. این شکل، یک نمای دوبعدی از المان مورد نظر را نمایش میدهد (راستای z به سمت داخل صفحه است).

برای شروع تحلیل، کرنش εx در راستای x را در نظر بگیرید. این کرنش باعث ایجاد تغییر طولی به اندازه εxdx در راستای محور x میشود. dx، طول ضلع المان در جهت مورد نظر را نمایش میدهد (شکل بالا). با ایجاد این تغییر طول، قطر المان به اندازه رابطه زیر افزایش مییابد:
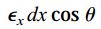
اکنون، کرنش εy در راستای y را در نظر بگیرید. این کرنش باعث ایجاد تغییر طولی به اندازه εydy در راستای محور y میشود. dy، طول ضلع المان در جهت مورد نظر را نمایش میدهد (شکل زیر).
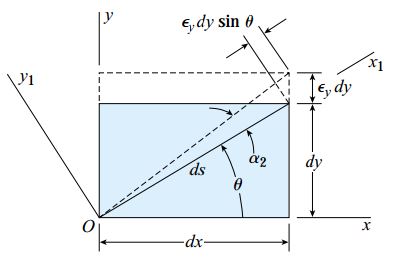
با ایجاد این تغییر طول، قطر المان به اندازه رابطه زیر افزایش مییابد:

در نهایت، کرنش برشی γxy در صفحه xy را در نظر بگیرید. این کرنش باعث ایجاد انحراف المان میشود. این انحراف، زاویه گوشه پایین چپ المان را به اندازه کرنش برشی کاهش میدهد. به این ترتیب، صفحه بالایی المان نسبت به صفحه پایینی به اندازه γxydy به سمت راست حرکت میکند (شکل زیر).

تغییر شکل به وجود آمده باعث افزایش قطر المان به اندازه رابطه زیر میشود:

افزایش کلی طول قطر (Δd) از جمع سه عبارت قبلی به دست میآید:

کرنش نرمال εx1 در راستای x1 از تقسیم افزایش طول قطر المان (Δd) بر طول اولیه آن (ds) به دست میآید:

از آنجایی که dx/ds=cosθ و dy/ds=sinθ، معادله تبدیل کرنش نرمال به صورت زیر خواهد بود:

بنابراین، در این بخش به معادلهای دست یافتیم که میزان کرنش نرمال در راستای x1 را با توجه به پارامترهای εy ،εx و γxy محاسبه میکند. همانگونه که قبلاً نیز به آن اشاره شد، با جایگذاری θ+90 به جای θ در معادله εx1، رابطه جداگانهای برای تعیین کرنش نرمال εy1 به دست میآید.
کرنش برشی γx1y1
اکنون کرنش برشی γx1y1 در صفحه x1y1 را مورد تحلیل قرار میدهیم. این کرنش با میزان کاهش زاویه بین محورهای x1 و y1 برابر است. برای درک بهتر این تحلیل، شکل زیر را در نظر بگیرید. این شکل، علاوه بر محورهای x1y1، محورهای xy را نیز نمایش میدهد. این دو دستگاه مختصات به اندازه زاویه θ با یکدیگر اختلاف دارند. تغییر شکلهای ناشی از کرنشهای εy ،εx و γxy باعث دوران پادساعتگرد خط Oa به اندازه زاویه α نسبت به محور x1 میشود. به همین ترتیب، خط Ob که در ابتدا بر روی محور y1 قرار داشت، به دلیل تغییر شکلهای به وجود آمده تحت زاویه β به صورت ساعتگرد دوران میکند.
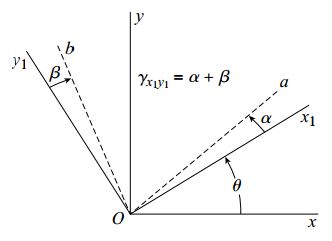
کرنش برشی γx1y1، کاهش زاویه بین دو خط Oa و Ob را نمایش میدهد. به این ترتیب:

بنابراین، به منظور یافتن کرنش برشی γx1y1، در ابتدا باید زوایای α و β را تعیین کنیم. زاویه α از طریق تغییر شکلهای نمایش داده شده در شکل زیر قابل محاسبه است. کرنش εx باعث دوران ساعتگرد قطر المان میشود. زاویه این دوران را با حرف α1 مشخص میکنیم. با توجه به شکل زیر، مقدار زاویه α1 از تقسیم εxdxsinθ بر طول قطر (ds) به دست میآید:

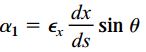
به همین ترتیب، کرنش εy باعث دوران پادساعتگرد قطر المان تحت زاویه α2 میشود. با توجه به شکل زیر، مقدار زاویه α2 از تقسیم εydycosθ بر طول قطر (ds) قابل محاسبه است:


در نهایت، کرنش γxy باعث دوران ساعتگرد قطر المان تحت زاویه α3 میشود. با توجه به شکل زیر، مقدار این زاویه از تقسیم γxydysinθ بر ds به دست میآید:


بنابراین، برآیند دورانِ پادساعتگرد قطر که در تصویر زیر نمایش داده شده است، از جمع زوایای α2 ،α1 و α3 حاصل میشود:


با توجه به اینکه dx/ds=cosθ و dy/ds=sinθ، رابطه بالا را میتوان به صورت زیر بازنویسی کرد:
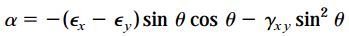
خط Ob در ابتدا به اندازه 90 درجه نسبت به خط Oa اختلاف داشت. به این ترتیب، با جایگذاری θ+90 به جای θ در معادله α، رابطهای برای تعیین مقدار زاویه دوران این خط (β) به دست میآید. دوران زاویه α به صورت پادساعتگرد و مثبت در نظر گرفته شده است. از اینرو، به دلیل ساعتگرد بودن دوران زاویه β، علامت آن منفی خواهد بود. بنابراین داریم:
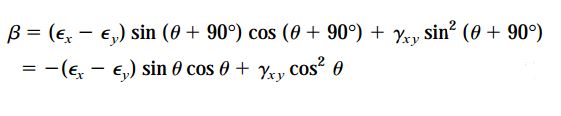
با اضافه کردن روابط مربوط به α و β در معادله کرنش برشی γx1y1 خواهیم داشت:
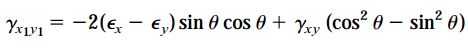
به منظور تبدیل معادله بالا به یک فرم کاربردیتر، تمام عبارات آن را تقسیم بر 2 میکنیم:

به این ترتیب در این بخش به معادلهای دست یافتیم که میتواند میزان کرنش برشی γx1y1 نسبت به محورهای x1y1 را با توجه به پارامترهای εy ،εx و γxy محاسبه کند.
معادلات تبدیل کرنش صفحهای
با استفاده از روابط مثلثاتی زیر میتوان معادلات ارائه شده در بخشهای قبل را با توجه به پارامتر 2θ بازنویسی کرد:
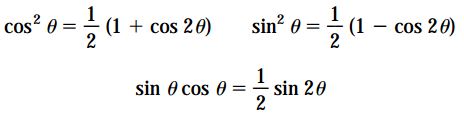
با در نظر گرفتن این روابط مثلثاتی، معادلات تبدیل کرنش صفحهای به فرم زیر درمیآیند:

و

با مقایسه پارامترهای موجود در معادلات تبدیل کرنش صفحهای و معادلات تبدیل تنش صفحهای میتوان مشاهده کرد که پارامتر εx1 معادل σx1، عبارت γx1y1/2 معادل τx1y1، پارامتر εx معادل σx، پارامتر εy معادل σy و عبارت γxy/2 معادل τxy است. جدول زیر، متغیرهای مشابه در هر یک از این دو معادلات تبدیل را نمایش میدهد:
| تنش | کرنش |
| εx | σx |
| εy | σy |
| γxy/2 | τxy |
| εx1 | σx1 |
| γx1y1 | τx1y1 |
تشابه بین معادلات تبدیل کرنش صفحهای و معادلات تبدیل تنش صفحهای نشان میدهد که تمامی مفاهیم ارائه شده در حالت تنش صفحهای دارای مفاهیم معادل در حالت کرنش صفحهای هستند. به عنوان مثال، حاصل جمع کرنشهای نرمال در جهتهای عمود بر هم مقداری ثابت است:

رابطه بالا را با رابطه ارائه شده در مبحث تنشهای نرمال مقایسه کنید:
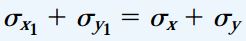
با جایگذاری متغیرهای معادل (در جدول بالا) میتوان تشابه بین مفاهیم کرنش صفحهای و تنش صفحهای را به راحتی مشاهده کرد. در ادامه به معرفی برخی از معادلات مشابه دیگر در حالت کرنش صفحهای میپردازیم.
کرنشهای اصلی
کرنشهای اصلی بر روی صفحات عمود با زاویه اصلی θp رخ میدهند. مقادیر زاویههای اصلی از رابطه زیر به دست میآیند:
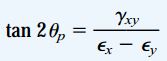
کرنشهای اصلی نیز از طریق رابطه کلی زیر محاسبه میشوند:

رابطه بالا مشابه رابطه کلی محاسبه تنشهای اصلی (σ1,2) است. در انتهای این مقاله، نحوه تعیین جهتگیری کرنشهای اصلی در قالب یک مثال توضیح داده خواهد شد. توجه داشته باشید که در حالت کرنش صفحهای، کرنش نرمال در راستای z و کرنشهای برشی بر روی صفحات اصلی صفر هستند.
کرنش برشی ماکسیمم
کرنش برشی ماکسیمم (γmax) بر روی صفحه xy با زاویه 45 درجه نسبت به راستای کرنشهای اصلی رخ میدهد. این کرنش از طریق رابطه زیر محاسبه میشود:

کرنش برشی مینیمم (γmin) با کرنش برشی ماکسیمم برابر اما علامت آن منفی است. مقدار کرنش نرمال در راستای کرنش برشی ماکسیم به صورت زیر تعیین میشود:

رابطه بالا مشابه رابطه زیر در مبحث تنشهای اصلی است:
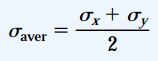
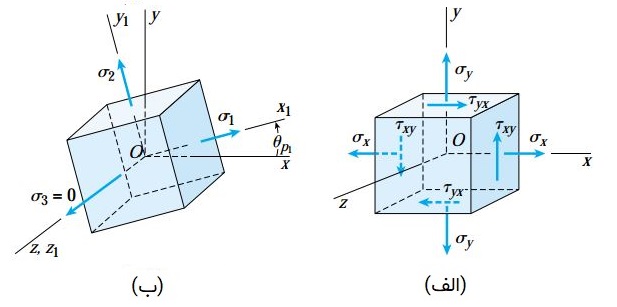
کرنشهای برشی ماکسیمم خارج صفحهای با استفاده از روابطی مشابه γmax/2 به دست میآیند. بخش ب شکل زیر، یک المان تحت تنش صفحهای را نمایش میدهد که جهتگیری آن در راستای صفحات اصلی تنش است و هیچ تنش برشی بر روی آن اعمال نمیشود. به این ترتیب، کرنش برشی γx1y1 بر روی این المان صفر خواهد بود. این بدان معناست که کرنشهای نرمال در این المان، کرنشهای اصلی هستند. بنابراین، بر روی هر نقطهای از جسم تحت تنش، کرنشهای اصلی و تنشهای اصلی در جهات یکسان رخ میدهند.
رسم دایره مور برای حالت کرنش صفحهای
مراحل رسم دایره مور برای حالت کرنش صفحهای مشابه مراحل رسم دایره مور برای حالت تنش صفحهای است. کرنش نرمال (εx1)، محور افقی دستگاه مختصات و نصفِ کرنش برشی (γx1y1/2)، محور عمودی مختصات را نمایش میدهد. طول مرکز دایره (نقطه C) نیز با مقدار کرنش نرمال میانگین (εaver) برابر است.
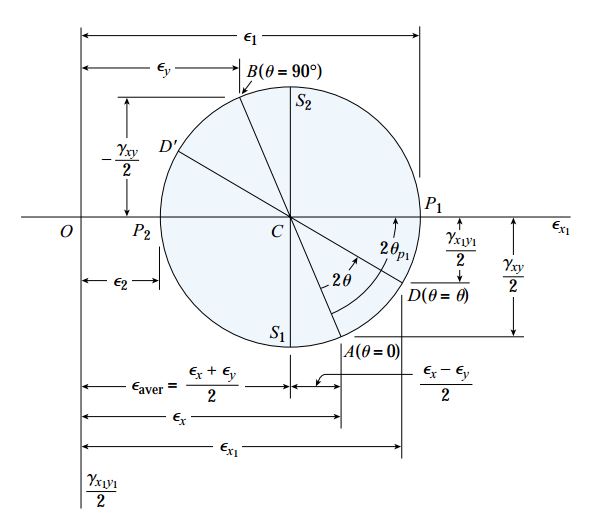
نقطه A بر روی دایره بالا، کرنشهای ایجاد شده راستای x یا θ=0 را نمایش میدهد. مختصات این نقطه (εx,γxy/2) است. نقطه B با مختصات (εy,-γxy/2)، در طرف مقابل نقطه A بر روی دایره مور قرار دارد. این نقطه، کرنشهای مربوط به محورهای دوران یافته تحت زاویه θ=90 را نمایش میدهد. کرنشهای مربوط به محورهای دورانیافته تحت زاویه θ، توسط نقطه D بر روی دایره مور مشخص میشوند.
این نقطه بر روی موقعیتی با اختلاف زاویه 2θ در جهت پادساعتگرد نسبت به شعاع CA قرار دارد. نقاط P1 و P2، مقدار کرنشهای اصلی را نشان میدهند. کرنشهای برشی ماکسیمم نیز با نقاط S1 و S2 مشخص شدهاند. مقادیر مربوط به تمام این کرنشها را میتوان هم با استفاده از دایره مور و هم با استفاده از معادلات تبدیل محاسبه کرد.
اندازهگیری کرنش
کرنشهای نرمال موجود بر روی سطح یک جسم تحت بارگذاری معمولاً با استفاده از یک کرنشسنج الکتریکی مورد اندازهگیری قرار میگیرند. ابعاد این کرنشسنجها بسیار کوچک است و طول آنها از 3 تا 13 میلیمتر تغییر میکند. این وسایل اندازهگیری به طور محکم بر روی سطح نمونه مورد آزمایش نصب میشوند تا تغییر طول آنها با کرنشهای ایجاد شده در نمونه متناسب باشد.
در تصویر زیر، نمونهای از یک کرنشسنج الکتریکی نمایش داده شده است. هر یک از گیجهای اندازهگیری دارای یک شبکه فلزی کوچک هستند که طول آن در هنگام ایجاد کرنش، افزایش یا کاهش مییابد. همانگونه در شکل زیر مشاهده میشود، یک سیم پیوسته به صورت رفت و برگشت دو انتهای این شبکه فلزی را به هم متصل کرده است. با افزایش یا کاهش طول نمونه، مقاومت الکتریکی این سیم تغییر میکند. سپس، تغییرات مقاومت سیم به مقادیر کرنش تبدیل میشوند. این گیجها حساسیت بسیار بالایی دارند و قادر به اندازهگیری کرنشهایی به کوچکی 6-10*1 هستند.

هر یک از گیجها کرنش نرمال را فقط در یک جهت اندازهگیری میکند. به علاوه، جهتگیری تنشهای اصلی معمولاً نامشخص است. با توجه به این دلایل، ترتیب قرارگیری گیجها باید به گونهای باشد که هر یک از آنها میزان کرنش در یک جهت خاص را مورد اندازهگیری قرار دهد. با جمعآوری اطلاعات به دست آمده از این اندازهگیریها میتوان میزان کرنش در هر جهت دلخواه را محاسبه گرد.
به مجموعهای از سه گیج که در یک الگوی بخصوص کنار یکدیگر قرار گرفتهاند، «گُل کرنش» (Strain Rosette) گفته میشود. به دلیل نصب گل کرنش بر روی سطح نمونه و وجود حالت تنش صفحهای در این ناحیه، میزان کرنشهای موجود در جهتهای مختلف را میتوان با استفاده از معادلات تبدیل کرنش صفحهای محاسبه کرد.
محاسبه مقادیر تنش با استفاده از مقادیر کرنش
معادلات کرنش ارائه شده در این مقاله تنها با استفاده از روابط هندسی المان به دست آمدند. از اینرو، این معادلات برای تمام مواد (خطی یا غیر خطی) قابل استفاده هستند. با این وجود، در صورت نیاز به محاسبه مقادیر تنش با استفاده از مقادیر کرنش، باید خواص مواد را نیز در نظر گرفت.
اگر ماده از قانون هوک پیروی کند، مقادیر تنش با استفاده از معادلات تنش-کرنش مناسب برای حالت تنش صفحهای یا تنش سهمحوری قابل محاسبه خواهند بود. به عنوان مثال، فرض کنید که ماده در شرایط تنش صفحهای قرار دارد و مقدار εy ،εx و γxy نیز توسط کرنشسنج به دست آمده است. در این وضعیت، میزان تنشهای درون ماده با کمک معادلات تنش-کرنش برای حالت تنش صفحهای و به صورت زیر تعیین میشوند.


اکنون یک حالت دیگر را در نظر بگیرید. فرض کنید که کرنشهای اصلی ε2 ،ε1 و ε3 را برای المان کوچکی از ماده تعیین کردهایم (در حالت کرنش صفحهای ε3=0 خواهد بود). با مشخص بودن مقادیر کرنشها، تنشهای اصلی با استفاده از قانون هوک در تنش سهمحوری قابل محاسبه خواهند بود:

پس از محاسبه تنشهای اصلی نیز میتوان تنشهای موجود بر روی صفحات دوران یافته را با کمک معادلات تبدیل برای تنش صفحهای تعیین کرد.
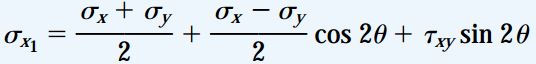
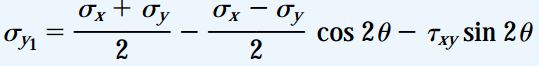
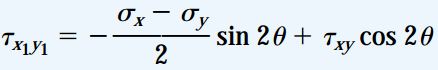
مثالهای کاربردی
در این بخش برای آشنایی بهتر با مفاهیم مرتبط با کرنش صفحهای و نحوه به کارگیری معادلات مرتبط با آن، به تشریح دو مثال میپردازیم.
مثال 1
المان کوچکی از یک ماده را مطابق شکل زیر در نظر بگیرید. این المان در حالت کرنش صفحهای قرار دارد و مقدار هر یک از کرنشهای به وجود آمده در آن به صورت زیر است:

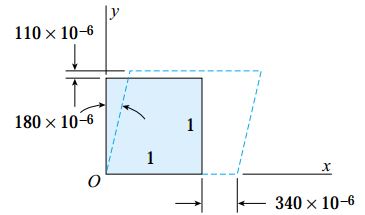
المان نمایش داده شده در شکل بالا دارای ابعاد واحد است. از اینرو، تغییرات به وجود آمده در ابعاد خطی با کرنشهای نرمال εx و εy هماندازه خواهند بود. کرنش برشی γxy نیز میزان کاهش زاویه در گوشه پایین چپ المان را نمایش میدهد. اکنون با توجه به اطلاعات مسئله، مقدار کمیتهای زیر را محاسبه کنید:
- الف) کرنشهای موجود در المان دوران یافته تحت زاویه θ=0
- ب) کرنشهای اصلی
- ج) کرنشهای برشی ماکسیمم
توجه: برای حل مسئله تنها کرنشهای درون صفحهای را در نظر بگیرید و نتایج به دست آمده را بر روی شکل المان دورانیافته نمایش دهید.
الف) کرنشهای موجود در المان دورانیافته تحت زاویه θ=0
کرنشهای درون یک المان دورانیافته تحت زاویه θ نسبت به محور x با استفاده از معادلات تبدیل εx1 و γx1y1/2 تعیین میشوند. برای شروع محاسبات، ابتدا مقادیر عبارات زیر را تعیین میکنیم:

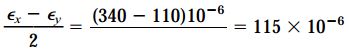

با جایگذاری مقادیر بالا در معادلات تبدیل خواهیم داشت:
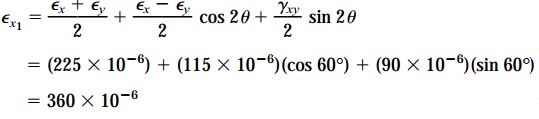
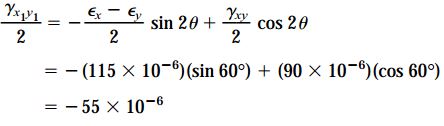
بنابراین مقدار تنش برشی برابر است با:

برای تعیین کرنش εy1 نیز از رابطه زیر استفاده میکنیم:
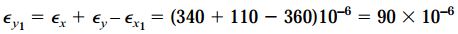
شکل زیر، مقادیر کرنشهای εy1 ،εx1 و γx1y1/2 برای یک المان دوران یافته تحت زاویه θ=0 را نمایش میدهد. توجه داشته باشید که به دلیل منفی بودن مقدار γx1y1، زاویه گوشه پایین چپ المان در حین اعمال کرنش افزایش مییابد.
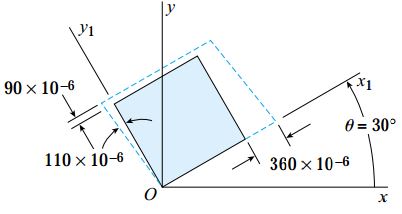
ب) کرنشهای اصلی
کرنشهای اصلی را میتوان به راحتی و با کمک رابطه کلی زیر محاسبه کرد:
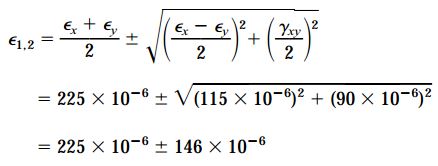
بنابراین:

با توجه به مقادیر به دست آمده، ε1 به عنوان کرنش اصلی ماکسیمم و ε2 به عنوان کرنش اصلی مینیمم در نظر گرفته میشود. زاویه صفحات اصلی نیز به صورت زیر به دست میآید:
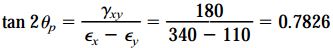
در بازه 0 تا 360، زوایای 38 و 218 در معادله بالا صدق میکنند. بنابراین، جهتگیری صفحات اصلی به صورت زیر خواهد بود:

برای مشخص کردن اینکه هر زاویه به کدامیک از کرنشهای اصلی اختصاص دارد، مقدار θp=19 را در اولین معادله تبدیل قرار میدهیم و میزان کرنش آن را محاسبه میکنیم:

بر اساس نتیجه به دست آمده، کرنش اصلی ماکسیمم (ε1) در زاویه θp1=19 و کرنش اصلی مینیمم (ε2) در زاویه θp2=109 قرار گرفته است. بنابراین:

توجه داشته باشید که:
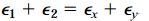
شکل زیر، کرنشهای اصلی المان را نمایش میدهد. فراموش نکنید که هیچ کرنش برشی بر روی صفحات اصلی وجود ندارد.

ج) کرنش برشی ماکسیمم
مقدار کرنش برشی ماکسیمم از طریق رابطه زیر به دست میآید:

موقعیت قرارگیری یک المان با کرنشهای برشی ماکسیمم، به اندازه 45 درجه نسبت به جهتهای اصلی اختلاف دارد. بنابراین:
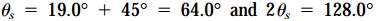
با جایگذاری 2θs=128 در دومین معادله تبدیل، علامت مربوط به این زاویه تعیین میشود. با توجه به این معادله داریم:
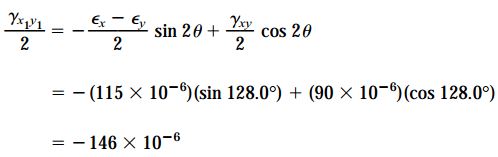
این نتیجه نشان میدهد که المان دورانیافته تحت زاویه θs2=64 در معرض کرنش برشی ماکسیمم منفی قرار دارد. مقدار زاویه θs1 همیشه به اندازه 45 درجه کمتر از زاویه θp1 است. بنابراین:

کرنشهای برشی مربوط به θs1 و θs2 به ترتیب برابر با γmax=290*10-6 و γmin=-290*10-6 هستند. علاوه بر این پارامترها، مقدار کرنشهای نرمال موجود بر روی المان نیز از رابطه زیر محاسبه میشود:
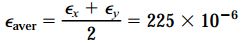
شکل زیر، المانی با کرنشهای برشی ماکسیمم درون صفحهای را نمایش میدهد.
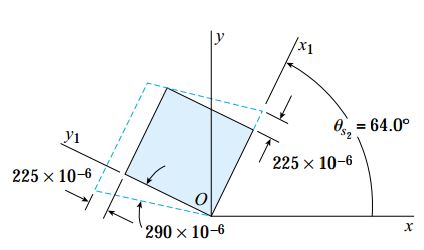
در این مثال، مقادیر مربوط به پارامترهای کرنشهای را با استفاده از معادلات تبدیل تعیین کردیم. توجه داشته باشید که تمام این نتایج به راحتی و با کمک رسم دایره مور نیز قابل محاسبه هستند.
مثال 2
شکل زیر، کرنشسنجی با سه مقاومت الکتریکی را نمایش میدهد. آرایش گیجهای کرنشسنج به گونهای است که بین هر دو گیج 45 درجه اختلاف وجود دارد. پیش از شروع بارگذاری، این کرنشسنج بر روی سطح سازه یا نمونه آزمایشگاهی نصب میشود. گیجهای B ،A و C نیز کرنشهای εb ،εa و εc را در راستای خطوط Ob ،Oa و Oc اندازهگیری میکنند.
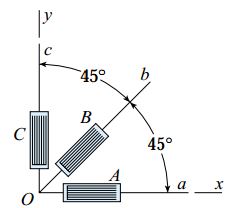
با توجه به شرایط مسئله، نحوه اندازهگیری کرنشهای εy1 ،εx1 و γx1y1 برای المان دوران یافته تحت زاویه θ نسبت به محورهای xy را توضیح دهید (شکل زیر).
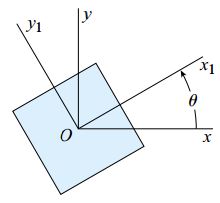
حالت تنش بر روی سطح خارجی اجسام تحت بارگذاری، به صورت صفحهای است. در این شرایط، معادلات تبدیل εx1 و γx1y1 برای هر دو حالت کرنش صفحهای و تنش صفحهای قابل استفاده هستند. بنابراین میتوان مقدار کرنش در هر جهت دلخواه را با استفاده از این معادلات محاسبه کرد.
کرنشهای مربوط به محورهای xy
حل مسئله را با تعیین کرنشهای مربوط به محورهای xy شروع میکنیم. گیجهای A و C به ترتیب با محورهای x و y همراستا هستند. به همین دلیل، کرنشهای اندازهگیری شده از این گیجها مقادیر εx و εy را مشخص میکنند:

به منظور تعیین کرنش برشی γxy از معادله تبدیل کرنشهای نرمال استفاده میکنیم:
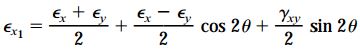
میدانیم که در زاویه θ=45، رابطه εx1=εb برقرار خواهد بود. بنابراین، معادله بالا به فرم زیر تبدیل میشود:
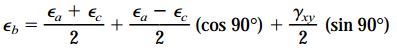
با حل این رابطه بر حسب γxy خواهیم داشت:
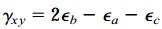
به این ترتیب، کرنشهای εy ،εx و γxy به راحتی و تنها با قرائت گیجهای کرنشسنج قابل تعیین خواهند بود.
کرنشهای مربوط به محورهای x1y1
با مشخص شدن کرنشهای εy ،εx و γxy و حل معادلات تبدیل εx1 و γx1y1 یا رسم دایره مور، میتوانیم کرنشهای موجود بر روی یک المان دوران یافته تحت زاویه θ نسبت به محورهای xy را محاسبه کنیم. علاوه بر این، کرنشهای اصلی و کرنشهای برشی ماکسیمم نیز با توجه به این پارامترها قابل تعیین خواهند بود.
^^












