ضریب همبستگی جزئی (Partial Correlation) — به زبان ساده

معمولا برای سنجش وابستگی بین دو متغیر از «ضریب همبستگی» (Correlation Coefficient) استفاده می‌شود. ولی ممکن است این وابستگی به دلیل ارتباط این دو متغیر با متغیر دیگری باشد که همزمان بر هر دو آن‌ها اثرگذار است. به این منظور برای اندازه‌گیری میزان خالص وابستگی بین دو متغیر باید از معیار دیگری کمک گرفت. در تئوری احتمال و آمار، «همبستگی جزئی» (Partial Correlation)، معیاری برای اندازه‌گیری وابستگی بین دو متغیر با حذف تاثیر متغیرهای دیگر است.

برای درک بهتر این نوشتار، بهتر است ابتدا با مفهوم ضریب همبستگی که در مطلب ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده آمده است آشنا باشید. همچنین مطالعه رگرسیون خطی — مفهوم و محاسبات به زبان ساده خالی از لطف نیست.

ضریب همبستگی جزئی

فرض کنید می‌خواهیم براساس داده‌های رشد مربوط به کودکان بین ۴ تا ۱2 سال، رابطه بین وزن و میزان کالری مصرفی را مشخص کنیم. از آنجایی معمولا وزن و مصرف کالری با سن کودکان رابطه دارد، بهتر است برای اندازه‌گیری میزان رابطه خالص بین وزن و مصرف کالری، عامل سن را کنترل کنیم و همبستگی بین دو متغیر اصلی را با حذف اثر این متغیر بدست آوریم.

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس در فرادرس

کلیک کنید

هر چه مصرف کالری در تغذیه کودک بیشتر باشد، انتظار می‌رود که وزن او نیز افزایش یابد. به نظر می‌رسد با توجه به سن کودکان نیز میزان مصرف کالری در آن‌ها افزایش یابد. بنابراین سن هم با وزن و هم با مصرف کالری در ارتباط است. برای کنترل و حذف اثر سن بر روی همبستگی بین وزن و مصرف کالری از ضریب همبستگی جزئی استفاده می‌شود.

نکته: اگر متغیرهای مورد بحث دارای توزیع توام چند متغیره نرمال باشند، ضریب همبستگی جزئی همان ضریب «همبستگی شرطی» (Conditional Correlation) خواهد بود.

تعریف ضریب همبستگی جزئی با متغیر کنترلی Z

اگر X و Y‌ دو متغیر تصادفی و Z نیز متغیر کنترلی باشد که با متغیرهای X و Y دارای وابستگی است، آنگاه ضریب همبستگی جزئی بین X و Y‌ با حذف اثر متغیر کنترلی Z را با $$\rho_{_{XY.Z}}$$‌ نشان می‌دهند و به صورت زیر محاسبه می‌کنند:

$$\large \rho_{_{XY.Z}}=\dfrac{\rho_{_{XY}}-\rho_{_{XZ}}\rho_{_{YZ}}}{(1-\rho^2_{_{XZ}})^\frac{1}{2}(1-\rho^2_{_{YZ}})^\frac{1}{2}}$$

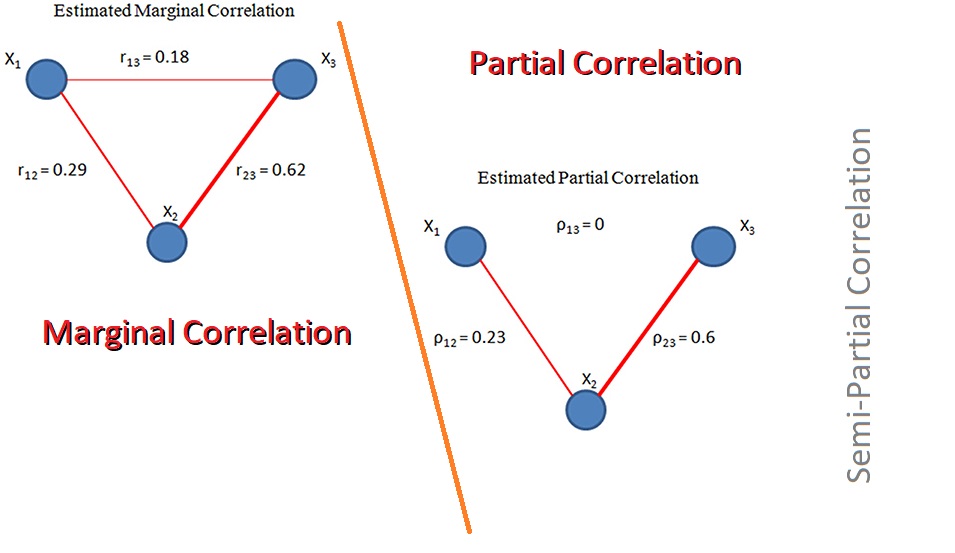
در این رابطه منظور از $$\rho_{XY}$$ همان ضریب همبستگی ساده بین X و Y است که در مقابل با ضریب همبستگی جزئی گاهی به آن «ضریب همبستگی حاشیه‌ای» (Marginal Correlation) می‌گویند. دامنه مقدارهای این ضریب به مانند ضریب همبستگی حاشیه‌ای در فاصله ۱- تا ۱ است. به این معنی که هرچه ضریب همبستگی جزئی به ۱ یا به ۱- نزدیک باشد، شدت رابطه بین دو متغیر با کنترل و حذف اثر متغیرهای دیگر بیشتر است و هر چه مقدار این ضریب به ۰ نزدیک باشد، بیانگر عدم وابستگی بین آن دو خواهد بود.

مثال 1

جدول شامل اطلاعات مربوط به وزن (برحسب کیلوگرم)، مصرف کالری (برحسب کیلوکالری) و سن ۶ کودک است.

با توجه به نحوه محاسبه ضریب همبستگی، مقدار ضریب همبستگی حاشیه‌ای بین وزن و مصرف کالری برابر است با:

$$\rho(X,Y)=\dfrac{\overline{XY}-\overline{X}\overline{Y}}{(s_X s_y)}=\dfrac{102.18-37.17\times 2.425}{17.544\times 0.8275}=0.8295$$

در این رابطه $$\overline{XY}$$ میانگین حاصلضرب و $$s_X$$ و $$s_Y$$ نیز انحراف استاندارد متغیرهای X و Y‌ محسوب می‌شوند. همچنین ضریب همبستگی بین متغیر Z با X و Z‌ با Y‌ را در زیر محاسبه کرده‌ایم.

$$\rho_{XZ}=0.917,\;\;\;\rho_{YZ}=0.938$$

این مقدارها نشان‌دهنده وابستگی شدید بین متغیرهای Z با دو متغیر دیگر است. بنابراین برای سنجش میزان وابستگی دو متغیر وزن و مصرف کالری باید اثر متغیر سن را از بین برد زیرا سن بر هر دو متغیر اثرگذار است. ضریب همبستگی جزئی در این حالت میزان وابستگی خالص بین وزن و مصرف کالری را بدون در نظر گرفتن سن محاسبه می‌کند.

$$\large \rho_{XY.Z}=\dfrac{\rho_{XY}-\rho_{XZ}\rho_{YZ}}{(1-\rho^2_{XZ})^\frac{1}{2}(1-\rho^2_{YZ})^\frac{1}{2}}=$$

$$\dfrac{0.8295-0.917 \times 0.938}{(1-0.917^2)^\frac{1}{2}\times (1-0.938^2)^\frac{1}{2}}=-0.2216$$

که نشان می‌دهد اگر سن تحت کنترل باشد (یعنی همه افراد دارای سن یکسانی باشند) وزن با مصرف کالری رابطه معکوس دارد. همانطور که دیده می‌شود، استفاده از ضریب همبستگی جزئی ممکن است حتی جهت ارتباط بین دو متغیر را معکوس نشان دهد.

برای انجام این گونه محاسبات می‌توانید از نرم‌افزار SPSS‌ برای بدست آوردن ضریب همبستگی جزئی استفاده کنید. به این منظور کافی است که متغیرهای مورد نظر را وارد کنید و از فهرست Analysis گزینه Correlate‌ و سپس گزینه Partial را انتخاب کنید. در پنچره ظاهر شده، متغیرهایی که می‌خواهید ضریب همبستگی جزئی بین آن‌ها محاسبه شود در کادر Variables قرار دهید. همچنین متغیر کنترلی را در کادر Controlling for بگذارید.

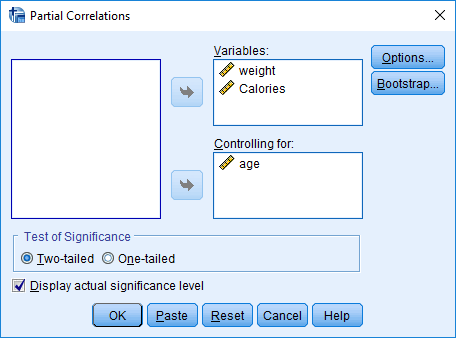
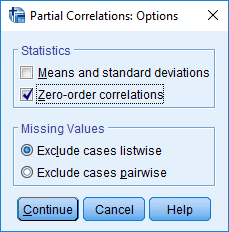
همچنین با انتخاب دکمه Options و گزینه Zero-order correlations، امکان محاسبه ضریب همبستگی ساده به همراه ضریب همبستگی جزئی وجود دارد. به این ترتیب اختلاف حاصل از حذف اثر متغیر کنترلی بهتر دیده می‌شود.

به عنوان نمونه، خروجی این دستور با تنظیمات گفته شده برای مثال ۱ در تصویر زیر قرار گرفته است.

توجه داشته باشید که اختلاف در بین ضریب محاسبه شده در SPSS‌ با ضریب بدست آمده در مثال به علت محاسبات براساس مقدارهای گرد شده است. در این جدول، در ستون اول متغیری که تحت کنترل قرار گرفته است، دیده می‌شود. از آنجایی که گزینه Zero-order correlation فعال شده در ابتدای جدول هیچ متغیری به عنوان متغیر کنترل دیده نمی‌شود ولی در قسمت دوم و پایین جدول متغیر age به عنوان متغیر کنترلی مشخص است.

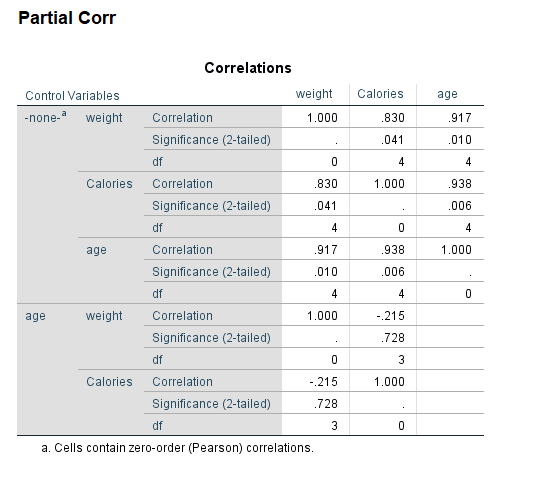
هر سطر نشانگر ضریب همبستگی (جزئی) یک متغیر با متغیرهای دیگر است. البته همانطور که دیده می‌شود ضریب همبستگی (جزئی) هر متغیر با خودش برابر با یک است. در سطر دوم نیز «مقدار احتمال» (p-Value) برای مقدار ضریب همبستگی (جزئی) قابل مشاهده است. درجه آزادی برای آماره ضریب همبستگی (جزئی) نیز در سطر سوم هر بخش از جدول دیده می‌شود.

نکته: همانطور که قابل رویت است ضریب همبستگی جزئی نیز مانند ضریب همبستگی، یک شاخص متقارن است، یعنی $$\rho_{XY,Z}=\rho_{YX,Z}$$.

ضریب همبستگی نیمه جزئی (Semipartial Correlation)

ضریب «همبستگی نیمه جزئی» (Semipartial Correlation) که گاهی «همبستگی بخشی» (Part Correlation) نیز نامیده می‌شود، مشابه ضریب همبستگی جزئی است با این تفاوت که اثر متغیر کنترلی فقط روی یک متغیر حذف می‌گردد.

فیلم آموزش منوی Test نرم افزار آماری MedCalc (رایگان) در فرادرس

کلیک کنید

بنابراین اگر ضریب همبستگی نیمه جزئی بین X و Y با کنترل اثر متغیر Z بر Y را به صورت $$\rho_{X(YZ)}$$‌ نشان دهیم، آن را به صورت زیر محاسبه خواهیم کرد:

$$\large \rho_{X(Y.Z)}=\dfrac{\rho_{XY}-\rho_{XZ}\rho_{YZ}}{(1-\rho^2_{YZ})^\frac{1}{2}}$$

بر همین اساس مشخص است که ضریب همبستگی نیمه جزئی بین X و Y به شرط کنترل اثر Z روی X برابر خواهد بود با:

$$\large \rho_{Y(X.Z)}=\dfrac{\rho_{XY}-\rho_{XZ}\rho_{YZ}}{(1-\rho^2_{XZ})^\frac{1}{2}}$$

بنابراین به نظر می‌رسد که این ضریب همبستگی متقارن نیست، یعنی $$\rho_{X(YZ)}\neq \rho_{Y(X.Z)}$$.

مثال ۲

طبق اطلاعات مربوط به مثال ۱، ضریب همبستگی نیمه جزئی $$\rho_{X(YZ)}$$‌ و $$\rho_{Y(XZ)}$$‌ به صورت زیر محاسبه می‌شوند:

$$\rho_{X(Y.Z)}=\dfrac{0.8295-0.917 \times 0.938}{(1-0.938^2)^\frac{1}{2}}=-0.08841$$

$$\rho_{Y(X.Z)}=\dfrac{0.8295-0.917 \times 0.938}{(1-0.917^2)^\frac{1}{2}}=-0.07683$$

برای محاسبه ضریب همبستگی نیمه جزئی، از نرم‌افزار SPSS‌ کمک می‌گیریم. کافی است از فهرست Analysis گزینه Regression و دستور Linear را انتخاب کنیم. اگر هدف محاسبه ضریب همبستگی نیمه جزئی X و Y با حذف اثر متغیر Z روی Y باشد تنظیمات پنجره را مطابق تصویر زیر انجام می‌دهیم.

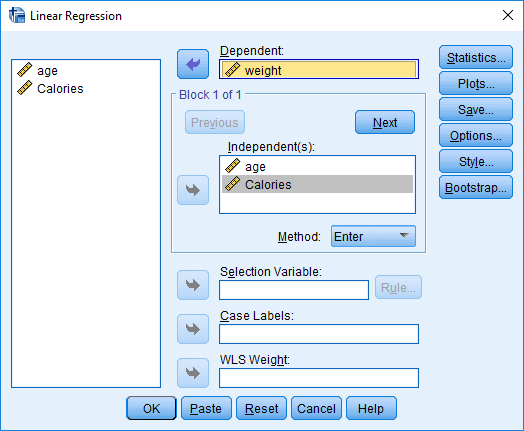
با انتخاب دکمه Statistics می‌توانید به پنجره محاسبه ضریب همبستگی نیمه جزئی و جزئی دسترسی پیدا کنید.

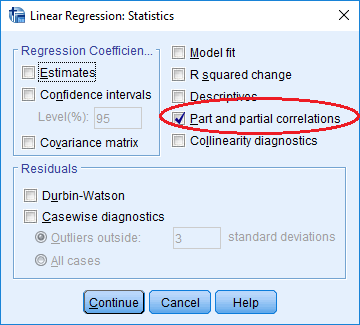
با این کار خروجی رگرسیون به همراه جدول مربوط به ضرایب همبستگی حاشیه‌ای (Zero-order)، جزئی (Partial) و نیمه جزئی (Part) خواهد بود که در سه ستون آخر به ترتیب از چپ به راست دیده می‌شوند. ضریب همبستگی نیمه جزئی در این جدول با محاسباتی که در  قسمت قبلی (0.08841-) انجام شد، تقریبا مطابقت دارد.

اگر می‌خواهید ضریب همبستگی نیمه جزئی را با کنترل متغیر سن روی وزن محاسبه کنید،‌ کافی است که در مدل رگرسیونی جای متغیر Weight و Calories را تغییر دهید تا محاسبات طبق جدول زیر حاصل شود:

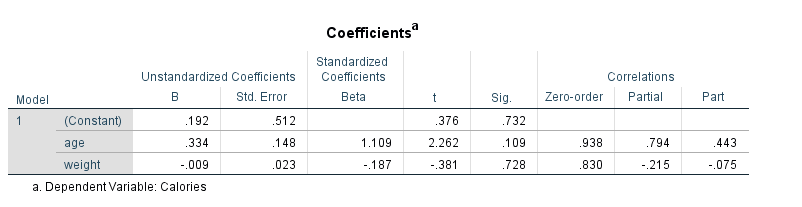
باز هم دیده می‌شود که نتیجه این خروجی با محاسبات قبلی (0.076-) تقریبا سازگار است. واضح است که کار با مقدارهای گرد شده، باعث این اختلاف در محاسبات شده است.

نکته: با توجه به شیوه محاسبه ضریب همبستگی نیمه جزئی، مشخص است که قدر مطلق مقدار آن همیشه از قدرمطلق ضریب همبستگی جزئی کوچکتر است زیرا مخرج کسر مربوط به محاسبه آن بزرگتر از ضریب همبستگی جزئی است.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش همبستگی و رگرسیون خطی در SPSS
• ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• رگرسیون غیر خطی در R — به زبان ساده
• مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری

^^