مدار RLC موازی – از صفر تا صد (+ دانلود فیلم آموزش رایگان)
در آموزشهای قبلی مجله فرادرس، درباره مدار RLC سری بحث کردیم. در این آموزش، مدار RLC موازی را بررسی میکنیم که در این مدار نیز، دو عنصر ذخیرهکننده انرژی وجود دارد. مدار RLC موازی، مداری مرتبه دوم است، زیرا پاسخ آن با معادلات دیفرانسیل مرتبه دوم توصیف میشود.
تحلیل مدار RLC موازی، مشابه تحلیل مدار RLC سری است. بنابراین، قبل از مطالعه این آموزش، پیشنهاد میکنیم آموزش مدار RLC سری را مطالعه کنید.
در این آموزش، ابتدا مدار را با شرایط اولیه عناصر ذخیرهکننده انرژی در نظر میگیریم. اگرچه ممکن است این مدارها شامل منابع وابسته باشند، اما در بخش اول، بدون منابع مستقل هستند. همانگونه که انتظار داریم، مدارهای بدون منبع، دارای پاسخ طبیعی هستند. در مرحله بعدی، مدار RLC موازی را با حضور منابع مستقل بررسی میکنیم که در این صورت، هم پاسخ گذرا و هم ماندگار خواهد داشت. مدارهای RLC موازی، در بسیاری از کاربردها عملی مانند شبکههای مخابراتی و طراحی فیلتر بهکار میروند.
مدار RLC موازی بدون منبع
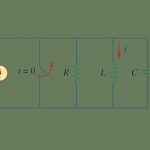
شکل ۱، مدار RLC بدون منبع را نشان میدهد.

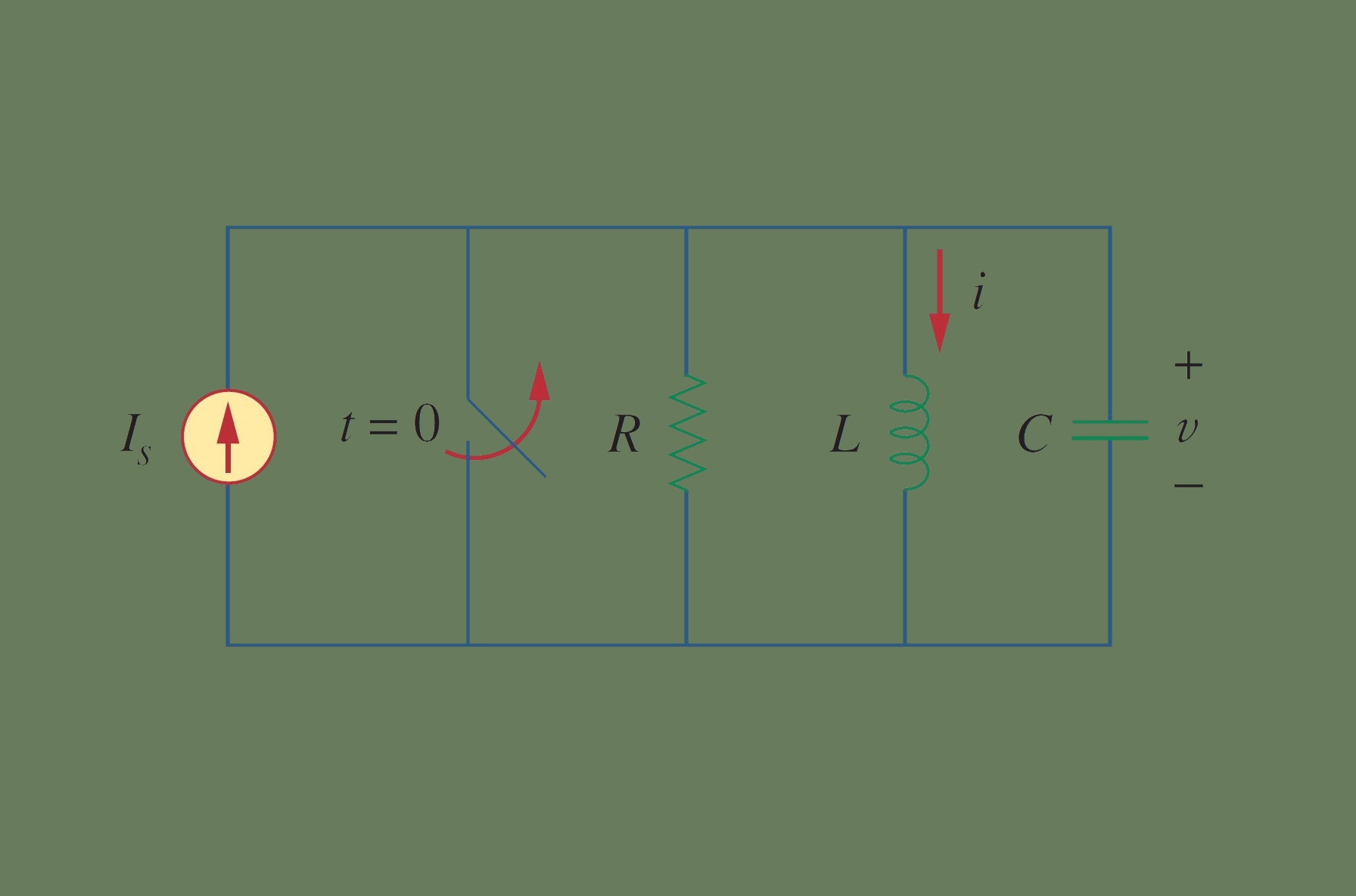
فرض کنید جریان اولیه سلف و ولتاژ اولیه خازن باشد:
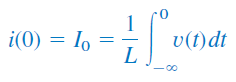
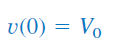
از آنجایی که سه عنصر با هم موازی هستند، ولتاژ آنها با هم برابر است. طبق قرارداد، جریان از سر مثبت به سه عنصر وارد میشود. با اعمال KCL به گره بالای مدار، داریم:
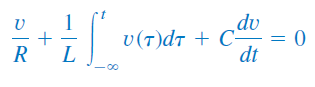
از معادله بالا نسبت به مشتق میگیریم و آن را بر تقسیم میکنیم:
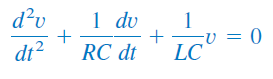
با جایگزینی مشتق اول و دوم رابطه بالا بهترتیب با و ، معادله مشخصه بهدست میآید. بنابراین، معادله مشخصه بهصورت زیر است:
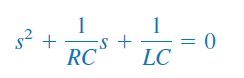
ریشه های معادله مشخصه را میتوان به شکل زیر بهدست آورد:
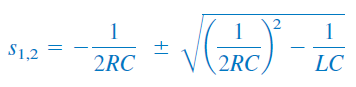
یا
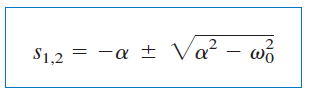
که در آن:
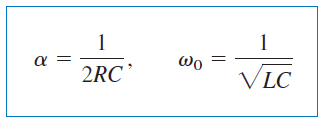
از آنجایی که ریشههای و مربوط به پاسخ فرکانسی مدار هستند، به آنها فرکانسهای طبیعی (Natural frequencies) میگوییم که برحسب نپر بر ثانیه () اندازهگیری میشوند. را فرکانس تشدید یا رزونانس (Resonant response) یا فرکانس طبیعی نامیرا مینامند و برحسب رادیان بر ثانیه () بیان میکنند. پارامتر ، فرکانس نپر (Neper frequency) یا ضریب میرایی (Damping factor) نامیده میشود و واحد آن، نپر بر ثانیه است. پاسخ مدار به سه رابطه ، یا بستگی دارد. در ادامه، این حالتها را بررسی میکنیم.
پاسخ فرامیرا ()
از رابطه (۶) میتوان نتیجه گرفت که اگر ، آنگاه باید . در این صورت، ریشههای معادله مشخصه، حقیقی و منفی خواهند بود. پاسخ مدار نیز بهصورت زیر است:
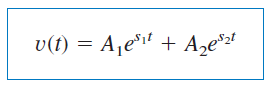
پاسخ میرای بحرانی ()
برای ، باید داشته باشیم . در این حالت، ریشهها حقیقی و برابر هستند. بنابراین، پاسخ مدار اینگونه است:
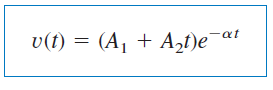
پاسخ فرومیرا ()
اگر ، آنگاه باید . در این صورت، ریشههای معادله مشخصه، مزدوج مختلط خواهند بود:
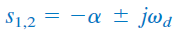
که در آن،
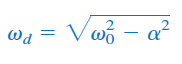
فرکانس میرایی (Damping frequency) نامیده میشود. هر دو فرکانس و ، فرکانس طبیعی هستند، زیرا به یافتن پاسخ طبیعی مدار کمک میکنند. فرکانس اغلب فرکانس طبیعی فرومیرا (Underdamped natural frequency) نامیده میشود. پاسخ مدار در این حالت بهصورت زیر است:
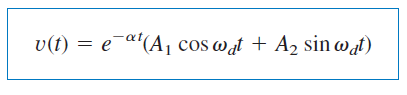
ثابتهای و از شرایط اولیه تعیین میشوند. در نتیجه، باید و را محاسبه کنیم. جمله نخست در رابطه (۱-ب) داده شد. جمله دوم را میتوان با کمک روابط (۱) و (۲) بهدست آورد:
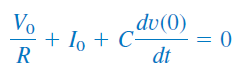
یا
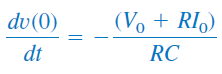
با بهدست آوردن ولتاژ خازن، در مدار RLC سری، میتوانیم سایر کمیتهای مدار را محاسبه کنیم. برای مثال، جریان مقاومت، از رابطه و جریان خازن با قابل محاسبه است.
پاسخ پله مدار RLC موازی
مدار RLC موازی شکل ۲ را در نظر بگیرید.
یک جریان dc را بهطور ناگهانی به مدار اعمال میکنیم. میخواهیم جریان را پیداکنیم.
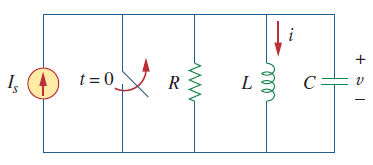
با اعمال KCL در گره بالای مدار، برای داریم:
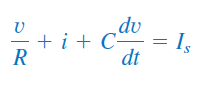
از آنجایی که ، رابطه بالا را میتوان بهفرم زیر نوشت:
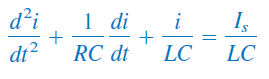
که مشابه معادله مشخصه رابطه (۳) است.
پاسخ کامل معادله (۱۴)، از پاسخ گذرای و پاسخ حالت ماندگار تشکیل شده است؛ یعنی:
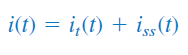
پاسخ ماندگار، مقدار نهایی است. در مدار شکل ۲، مقدار نهایی جریان گذرنده از سلف، برابر با جریان منبع است. بنابراین:
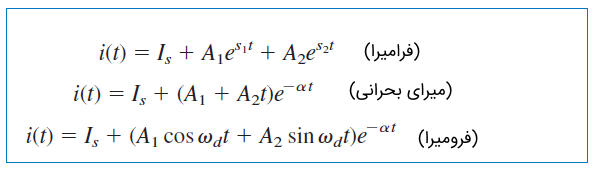
ثابتهای و را میتوان از شرایط اولیه و تعیین کرد. سایر متغیرهای مدار نیز با کمک ولتاژ بهدست میآیند؛ مثلاً جریان مقاومت، و جریان خازن، است.
پاسخ کامل هر متغیر مدار را میتوان مستقیماً با استفاده از رابطه زیر محاسبه کرد:
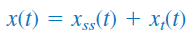
که در آن، و بهترتیب، مقدار نهایی و پاسخ گذرا هستند.
مثال
جریانهای و مدار شکل 3 را برای بهدست آورید.
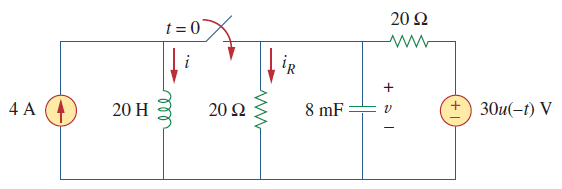
حل: در ، کلید باز است و مدار به دو قسمت مجزا تقسیم میشود. جریان منبع ۴ آمپری از سلف عبور میکند، بنابراین، .
از آنجایی که وقتی است، و وقتی است، ، منبع ولتاژ در به مدار اعمال میشود. در این حالت، خازن مانند یک مدار باز عمل میکند و ولتاژ آن برابر با ولتاژ مقاومت 20 اهمی موازی با آن است. با استفاده از تقسیم ولتاژ، ولتاژ اولیه خازن برابر است با:
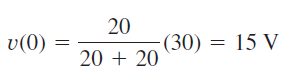
در ، کلید بسته میشود و یک مدار RLC موازی با یک منبع جریان داریم. در این حالت، منبع ولتاژ صفر، مانند اتصال کوتاه است. اکنون دو مقاومت ۲۰ اهمی با هم موازی هستند و حاصل آنها برابر است با . ریشههای مشخصه را میتوان بهصورت زیر تعیین کرد:
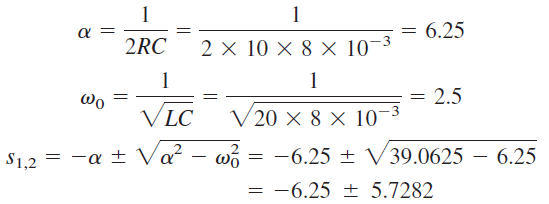
یا
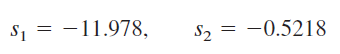
از آنجایی که ، پاسخ فرامیرا است. بنابراین، جریان بهفرم زیر است:
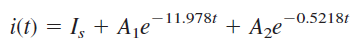
که در آن، مقدار نهایی است. اکنون از شرایط اولیه برای محاسبه و استفاده میکنیم. در داریم:
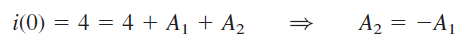
با مشتقگیری از معادله (۱۸)، میتوان نوشت:
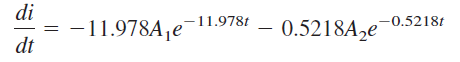
بنابران، در داریم:
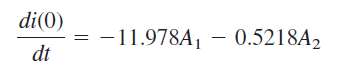
همچنین میتوانیم رابطه زیر را بنویسیم:
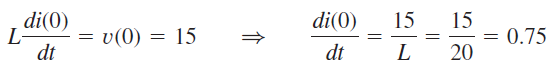
با جایگذاری مقدار اخیر در رابطه (۱۹) و (20)، مقدار بهصورت زیر بهدست میآید:
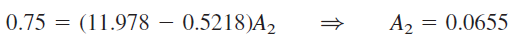 " width="518" height="43">
" width="518" height="43">
بنابراین، و . با جایگذاری این دو عدد در رابطه (۱۸)، پاسخ کامل مدار محاسبه میشود:
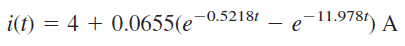
اکنون که را محاسبه کردهایم، میتوانیم ولتاژ را از رابطه و با استفاده از آن، جریان را بهدست آوریم:
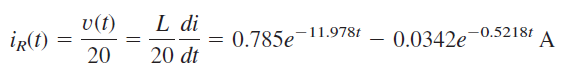
در صورتی که مباحث بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط، مطالب بیشتری یاد بگیرید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
^^













سلام. باتشکر از توضیحات جانع و کانلتون اگر امکانش هیت پاسخ حالت ضربه مدار RLC را هم اضافه کنید.
سلام
برای این منظور ابتدا پاسخ ضربه را محاسبه کنید و بعد ازش مشتق بگیرید
حاصل مشتق همون پاسخ پله هست