متغیر تصادفی و توزیع دو جمله‌ ای منفی – به زبان ساده

در تئوری احتمالات و آمار، توزیع دو جمله ای منفی، به عنوان یک توزیع گسسته شناخته شده است. با توجه به ارتباط این توزیع با آزمایش برنولی، مشخص است که بسیاری از پدیده‌های تصادفی ممکن است از این توزیع پیروی کنند. از توزیع دو جمله‌ای منفی بخصوص در بررسی‌های پزشکی و صنعتی استفاده می‌شود. اگر متغیر تصادفی X، تعداد موفقیت در یک دنباله از آزمایش‌های برنولی مستقل و هم توزیع (iid) پیش از r شکست، در نظر گرفته شود، می‌توان توزیع احتمال X را «دو جمله‌ای منفی» (Negative Binomial) در نظر گرفت.

برای مثال تعداد روزهایی که یک دستگاه کار می‌کند تا دچار مشکل شود از توزیع دوجمله‌ای منفی پیروی می‌کند. البته به شرطی که احتمال کار کردن آن در هر روز ثابت باشد. به عنوان یک مثال دیگر می‌توان تعداد شوت به دروازه تا رسیدن به rامین گل را به عنوان متغیر تصادفی دوجمله‌ای منفی در نظر گرفت. در اینجا می‌توان فرض کرد که رسیدن به گل شکست و به ثمر نرسیدن گل موفقیت است.

اگر با مفاهیم متغیر تصادفی و تابع احتمال آشنایی ندارید، بهتر است برای مطالعه این نوشتار ابتدا مطب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کرده باشید. همچنین خواندن مطلب متغیر تصادفی و توزیع برنولی — به زبان ساده خالی از لطف نیست.

توزیع دو جمله‌ای منفی

فرض کنید دنباله‌ای از آزمایش‌های تصادفی برنولی با شانس موفقیت p داشته باشیم. در این حالت، نتیجه هر آزمایش با احتمال $$p$$ برابر با ۱ و با احتمال $$1-p$$ نیز برابر با ۰ است. می‌دانیم که مقدار ۱ نشاندهنده موفقیت و ۰ نشانگر شکست است. این آزمایش تا زمانی که r شکست رخ دهد، ادامه پیدا می‌کند.

اگر X تعداد موفقیت‌ها تا پایان آزمایش باشد، می‌توان گفت که توزیع این متغیر تصادفی، دوجمله‌ای منفی با پارامترهای r و $$p$$ است. در این حالت می‌نویسیم $$\large X\sim NB(r,p)$$ و می‌خوانیم X دارای توزیع دوجمله‌ای منفی با پارامترهای $$p$$ و r است.

با توجه به تعریف این متغیر تصادفی مشخص است که تکیه‌گاه آن همه اعداد صحیح نامنفی است. یعنی می‌توان نوشت:

$$\large S=\{0,1,2,\ldots \}$$

متغیر تصادفی دو جمله‌ای منفی

اگر X یک متغیر تصادفی با تکیه‌گاه $$\large S=\{0,1,2,\ldots \}$$ باشد، توزیع احتمال آن را دوجمله‌ای منفی در نظر می‌گیریم اگر تابع احتمال آن به صورت زیر باشد.

$$\large \displaystyle f(k;r,p)\equiv \Pr(X=k)={\binom {r+k-1}{k}}p^{k}(1-p)^{r}$$

مشخص است که در اینجا r تعداد شکست‌ها و k نیز تعداد موفقیت‌ها است. همچنین $$p$$ نیز احتمال موفقیت در هر بار انجام آزمایش برنولی است. در این حالت X تعداد موفقیت‌ها تا rامین شکست در نظر گرفته می‌شود. با استفاده از رابطه‌ای که برای جایگشت‌ها داریم نیز می‌دانیم که رابطه زیر نیز برقرار است:

$$\large \displaystyle {\binom {k+r-1}{k}}={\frac {(k+r-1)!}{(k)!\,(r-1)!}}={\frac {(k+r-1)(k+r-2)\dotsm (r)}{(k)!}}$$

نکته: با توجه به ضرایب چند جمله‌ای‌ها، رابطه زیر را برای $$0\leq p<1$$ می‌توان نوشت:

$$\large \displaystyle (1-p)^{-r}=\sum _{k=0}^{\infty }{\binom {-r}{k}}(-p)^{k}=\sum _{k=0}^{\infty }{\binom {k+r-1}{k}}p^{k}$$

با توجه به نکته بالا به راحتی قابل مشاهده است که جمع تابع احتمال توزیع دو جمله‌ای منفی روی تکیه‌گاه برابر با ۱ است. با توجه به پارامتر r، نمودار مربوط به تابع احتمال این متغیر تصادفی به صورت زیر قابل نمایش است.

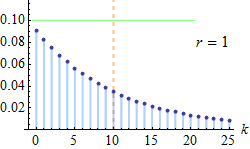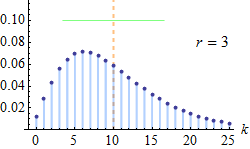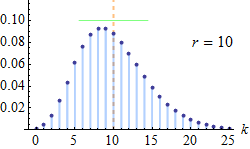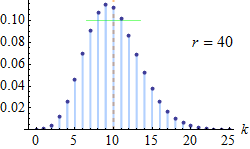
همانطور که دیده می‌شود با افزایش تعداد آزمایش‌ها (r+k)، توزیع به سمت نرمال نزدیک می‌شود.

البته ممکن است متغیر تصادفی X را به صورت‌های دیگری نیز تعریف کنند. در نتیجه تابع احتمال مقداری متفاوت خواهد بود. جدول زیر به بررسی تعریف‌های مختلف برای توزیع دوجمله‌ای منفی و تابع احتمال آن پرداخته است. توجه داشته باشید که در ستون اول (از راست) این جدول، مفهوم و مقداری که متغیر تصادفی X خواهد داشت مشخص شده است.

همانطور که دیده می‌شود، تفاوتی که بین تابع احتمال توزیع دوجمله‌ای با دوجمله‌ای منفی وجود دارد، عبارت n-1‌ در ترکیب‌ها است. از آنجایی که در توزیع دو جمله‌ای منفی، تعداد شکست‌ها باید برابر با r باشد تا آزمایش تصادفی برنولی خاتمه یابد، واضح است که نتیجه آخرین آزمایش شکست است. بنابراین فقط n-1 آزمایش باقی می‌ماند تا r-1 شکست و k موفقیت‌ها در آن پخش شوند.

برای محاسبه تابع احتمال تجمعی این توزیع نیز کافی است که به صورت زیر محاسبات را انجام دهیم.

$$\large \displaystyle F_X(x)=P(X\leq x)=\sum_{y=0}^xP(X=y)$$

به این معنی که باید مقدار تابع احتمال را برای همه مقدارهای کوچکتر یا مساوی با x با یکدیگر جمع کنیم.

خصوصیات توزیع دوجمله‌ای منفی

با توجه به ارتباطی که این توزیع با آزمایش برنولی دارد، می‌توان خصوصیات مختلفی برای آن جستجو کرد. ابتدا به تعمیم توزیع دوجمله‌ای منفی پرداخته سپس امید ریاضی و واریانس این متغیر تصادفی را محاسبه می‌کنیم. در انتها نیز ارتباط آن را با توزیع هندسی بررسی می‌کنیم.

فیلم آموزش متغیرهای تصادفی پیوسته (رایگان) در فرادرس

کلیک کنید

توزیع دوجمله‌ای منفی تعمیم یافته

اگر فرض کنیم که r یک عدد حقیقی مثبت باشد (البته در این حالت دیگر به معنی تعداد شکست نخواهد بود) باز هم می‌توان براساس تابع گاما که جایگزینی برای تابع فاکتوریل اعداد حقیقی است، محاسبه تابع چگالی احتمال را انجام داد.

$$\large \displaystyle f(k;r,p)\equiv \Pr(X=k)={\frac {\Gamma (k+r)}{k!\,\Gamma (r)}}p^{r}(1-p)^{k}\quad {\text{for }}k=0,1,2,\dotsc$$

این توزیع به افتخار ریاضیدان بزرگ «جورج پولیا» (Goerge Polya) دانشمند مجارستانی به نام توزیع پولیا (polya) شهرت دارد.

امید ریاضی و واریانس

از آنجایی که این متغیر تصادفی گسسته است برای محاسبه امید ریاضی آن از جمع استفاده خواهیم کرد. در نتیجه خواهیم داشت:

$$\large \displaystyle E(X)=\sum_{y=0}^{\infty}yP(X=y)=\dfrac{pr}{1-p}$$

برای مثال اگر متغیر تصادفی X به صورت $$X\sim NB(10,0.2)$$ باشد، امید ریاضی آن برابر با $$E(X)=\frac{0.2 \times 10}{1-0.2}=\frac{2}{0.8}=2.5$$ خواهد بود. به این معنی که برای رسیدن به ۱۰ شکست در دنباله‌ای از آزمایش‌های برنولی با احتمال موفقیت 0.2، به طور متوسط 2.5 پیروزی خواهیم داشت.

به همین ترتیب واریانس برای متغیر تصادفی با توزیع دوجمله‌ای منفی، به صورت زیر محاسبه می‌شود.

$$\large Var(X)=\dfrac{pr}{(1-p)^2}$$

به این ترتیب برای مثال قبل، واریانس تعداد موفقیت‌ها برای رسیدن به ۱۰ شکست برابر با 3.12۵ است.

ارتباط با توزیع‌ هندسی

در دیگر نوشته فرادرس با عنوان متغیر تصادفی و توزیع هندسی — به زبان ساده فرا گرفتیم که تعداد آزمایش‌های لازم برای رسیدن به اولین موفقیت، از توزیع هندسی پیروی می‌کند. از‌ آنجایی که توزیع دو جمله‌ای منفی تعداد موفقیت‌ها تا رسیدن به rامین شکست تلقی می‌شود، می‌توان آن را جمع r متغیر تصادفی هندسی با پارامتر $$1-p$$ در نظر گرفت.

در این حالت اگر $$X_1,X_2,\ldots ,X_r$$ متغیر تصادفی مستقل و هم‌توزیع هندسی با پارامتر $$1-p$$ و تکیه‌گاه $$S=\{0,1,2,\ldots \}$$ باشند، می‌توان نوشت:

$$\large \displaystyle Y_r=\sum_{i=1}^rX_i\sim NB(r,p)$$

با توجه به این موضوع امید ریاضی و واریانس توزیع دوجمله‌ای منفی به راحتی محاسبه می‌شود.

مسئله فروش آبنبات

یک دانش‌آموز برای گردش علمی تابستانی احتیاج به پول دارد. او برای کسب درآمد تصمیم می‌گیرد که تعدادی آبنبات به همسایگان بفروشد. در محله او ۳۷ خانه وجود دارد. اگر او ۵ آبنبات بفروشد، هزینه گردش علمی را تهیه کرده است.

احتمال اینکه آخرین (۵امین) آبنبات را در خانه nام بفروشد چقدر است؟ البته این شرط را نیز داریم که احتمال خرید آبنبات در هر خانه ثابت و برابر با 0.6 است.

به یاد داریم که یکی از حالت‌های محاسبه تابع احتمال برای متغیر تصادفی دوجمله‌ای منفی، احتمال k شکست برای رسیدن به rامین موفقیت در r+k=n آزمایش برنولی با پارامتر موفقیت p در نظر گرفته شد به شرطی که نتیجه آخرین آزمایش، موفقیت باشد. در این حالت فروش ۵ آبنبات، متناظر با ۵ موفقیت است. تعداد آزمایش‌ها نیز که برابر با n=k+5 است، تعداد خانه‌هایی را نشان می‌دهد که دانش‌آموز باید برای فروش به آن‌ها مراجعه کند.

پس می‌توان نوشت:

$$\large X \sim NB(5,0.4)$$

به این ترتیب، براساس تابع  احتمال متغیر تصادفی دوجمله‌ای منفی داریم:

$$\large P(X=n)= \displaystyle {(n-5)+5-1 \choose n-5}\;(1-0.4)^{5}\;0.4^{n-5}={n-1 \choose n-5}\;2^{5}\;{\frac {3^{n-5}}{5^{n}}}$$

البته باید توجه داشت که در اینجا $$n\geq 5$$ در نظر گرفته شده است. پس احتمال اینکه او پس از عبور از خانه دهم، ۵ آبنبات فروخته باشد برابر با 0.010033 است. همینطور احتمال اینکه تا قبل از رسیدن به نهمین خانه، ۵ آبنبات فروخته باشد به صورت زیر محاسبه می‌شود.

$$\large P(X=5)+P(X=6)+P(X=7)+P(X=8)=$$

$$0.01024+0.03072+0.055296+0.0774144=0.17367$$

اگر مطلب بالا برایتان مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی: میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای — به زبان ساده
• متغیر تصادفی و توزیع هندسی — به زبان ساده

^^