آشنایی کامل با دایره مور — تعیین مولفه های تنش در دو بعد و سه بعد

«دایره مور» (Mohr’s Circle)، یک روش گرافیکی و دوبعدی برای انجام تبدیلات «تانسور تنش کوشی» (Cauchy Stress Tensor) یا همان تانسور تنش واقعی است که در سال 1882 توسط «کریستین اتو مور» (Christian Otto Mohr) توسعه یافت.در این مقاله، به آشنایی با مفاهیم مرتبط با دایره مور، نحوه رسم آن و تعیین حالت کلی تنش در دو و سه بعد با استفاده از این دایره خواهیم پرداخت.

اگر جسمی را به صورت پیوسته در نظر بگیریم و بر روی آن تحلیل تنش انجام دهیم، امکان تعیین مؤلفه‌های تانسور تنش کوشی نقاط درون آن، با توجه به دستگاه مختصات مرجع فراهم می‌شود. پس از این کار می‌توان از دایره مور برای به دست آوردن مؤلفه‌های تنش اعمال شده در یک دستگاه مختصات دوران یافته استفاده کرد.

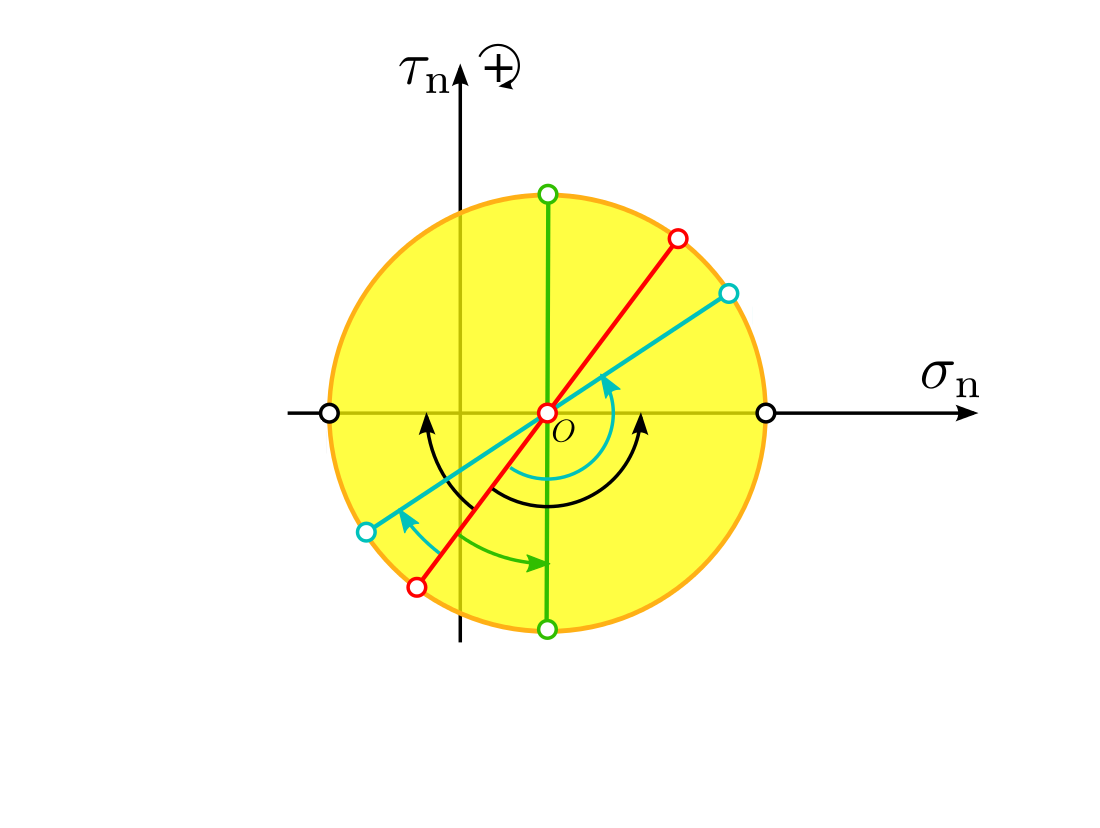
طول و عرض هر نقطه بر روی دایره مور، به ترتیب بیانگر مقدار مؤلفه‌های تنش نرمال (σ_n) و تنش برشی (τ_n) اعمال شده در دستگاه مختصات دوران یافته هستند. به عبارت دیگر، دایره مور مکان هندسی نقاطی است که حالت تنش صفحات منحصر به فرد در تمام جهات را نشان می‌دهند. به این ترتیب، محورهای مختصات، محورهای اصلی المان تنش خواهند بود.

«کارل کولمن» (Carl Culmann)، یکی از مهندسان سازه آلمانی در قرن 19 میلادی، اولین شخصی بود که از یک روش گرافیکی برای نمایش تنش‌ها (در خمش تیرهای افقی) استفاده کرد. مور، کاربرد این روش را برای تحلیل تنش‌های دوبعدی و سه‌بعدی تعمیم داد و باعث توسعه یک معیار شکست بر مبنای مفهوم دایره تنش شد. به طور کلی، دایره مور برای تمام ماتریس‌های متقارن 2*2 از جمله تانسورهای کرنش و ممان اینرسی کاربرد دارد.

کاربرد اصلی دایره مور

با اعمال نیروهای خارجی بر یک جسم شکل‌پذیر و پیوسته، نیروهای داخلی در بین ذرات آن تشکیل می‌شوند. این نیروها از قوانین حرکت اویلر برای محیط‌های پیوسته پیروی می‌کند (معادل قوانین حرکت نیوتن برای یک ذره).

یکی از معیارهای اندازه‌گیری شدت این نیروهای داخلی، تنش است. از آنجایی که محیط پیوسته در نظر گرفته می‌شود، نیروهای داخلی نیز به صورت پیوسته درون جسم توزیع خواهند شد.

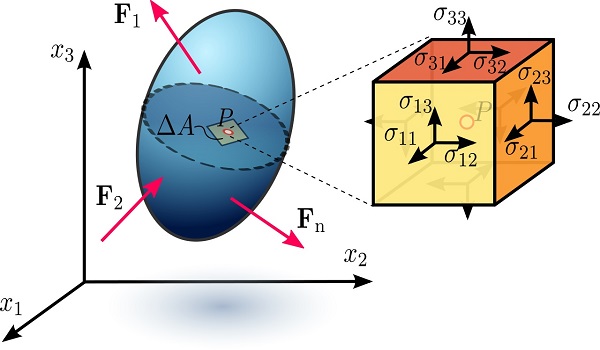
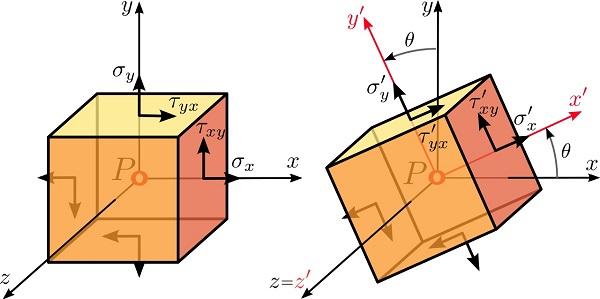
در مهندسی ژئوتکنیک، مکانیک و سازه، توزیع تنش درون یک جسم (مانند تنش در توده سنگ دیواره تونل، بال‌های هواپیما یا ستون‌های ساختمان) از طریق تحلیل تنش به دست می‌آید. با محاسبه توزیع تنش، تعیین تنش‌های موجود در هر نقطه درون جسم نیز امکان‌پذیر می‌شود. بر اساس مطالعات کوشی، وضعیت تنش در هر نقطه از یک جسم پیوسته، با استفاده از 9 مؤلفه تنش در یک تانسور مرتبه دوم قابل توصیف است (شکل بالا). این تانسور با عنوان «تانسور تنش کوشی» (Cauchy stress tensor) شناخته می‌شود:

$${\boldsymbol {\sigma }}=\left[{{\begin{matrix}\sigma _{{11}}&\sigma _{{12}}&\sigma _{{13}}\\\sigma _{{21}}&\sigma _{{22}}&\sigma _{{23}}\\\sigma _{{31}}&\sigma _{{32}}&\sigma _{{33}}\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{{xx}}&\sigma _{{xy}}&\sigma _{{xz}}\\\sigma _{{yx}}&\sigma _{{yy}}&\sigma _{{yz}}\\\sigma _{{zx}}&\sigma _{{zy}}&\sigma _{{zz}}\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}&\tau _{{xz}}\\\tau _{{yx}}&\sigma _{y}&\tau _{{yz}}\\\tau_{{zx}}&\tau _{{zy}}&\sigma _{z}\\\end{matrix}}}\right]$$

پس از تعیین توزیع تنش درون جسم نسبت به دستگاه مختصات (x,y)، ممکن است نیاز باشد که مؤلفه‌های تانسور تنش در یک نقطه بخصوص (مانند P) نسبت به یک دستگاه مختصات دوران یافته (′x′,y) نیز محاسبه شوند. به این ترتیب، باید مقدار تنش‌های اعمال شده بر صفحه گذرنده از نقطه P با جهت‌گیری متفاوت (دارای زاویه مشخص با دستگاه مختصات اولیه) را به دست آورد (شکل زیر).

به عنوان مثال در اینگونه مسائل، معمولاً یافتن مقادیر تنش نرمال ماکسیمم و تنش برشی ماکسیمم به همراه صفحه اعمال آن‌ها مورد توجه قرار می‌گیرد. به این منظور باید تبدیلات تانسور تنش را تحت یک دستگاه مختصات دوران یافته انجام داد. با توجه به تعریف تانسور، تانسور تنش کوشی از قانون تبدیل تانسور پیروی می‌کند و یکی از روش‌های نمایش گرافیکی تبدیلات آن، استفاده از دایره مور است.

تعیین حالت کلی تنش در دو بعد

در تحلیل دوبعدی، به منظور تعریف تانسور تنش در یک نقطه مشخص (P) نسبت به دو راستای دلخواه عمود بر هم (x,y)، تنها به سه مؤلفه تنش نیاز است. برای دستگاه مختصات (x,y)، این سه مؤلفه شامل تنش برشی (τ_xy) و تنش‌های نرمال (σ_x) و (σ_y) می‌شود. تانسور تنش کوشی دارای تقارن است و این تقارن را می‌توان به وسیله تعادل گشتاور زاویه‌ای نمایش داد. به این ترتیب، رابطه τ_xy=τ_yx برقرار خواهد بود. با توجه به نکات اشاره شده، تانسور تنش کوشی به صورت زیر نوشته خواهد شد:

$${\boldsymbol {\sigma }}=\left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}&0\\\tau _{{xy}}&\sigma _{y}&0\\0&0&0\\\end{matrix}}}\right]\equiv \left[{{\begin{matrix}\sigma _{x}&\tau _{{xy}}\\\tau _{{xy}}&\sigma _{y}\\\end{matrix}}}\right]$$

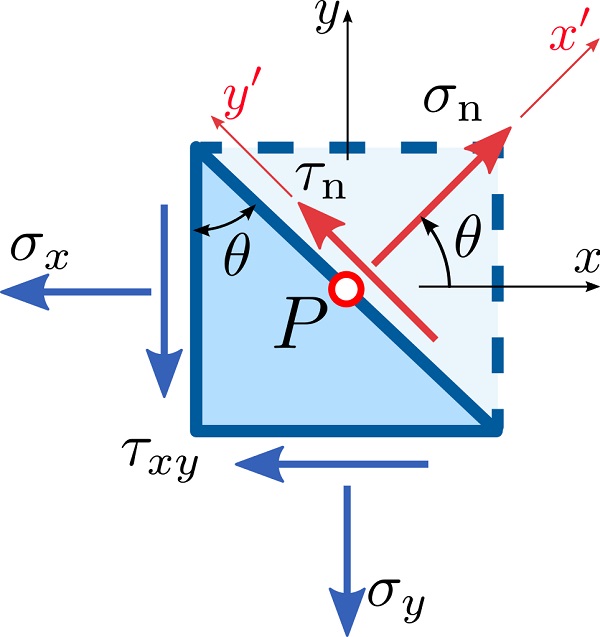
هدف از به کارگیری دایره مور، یافتن مؤلفه‌های تنش σ_n و τ_n در یک دستگاه مختصات دوران یافته (′x′,y) است که با مختصات اولیه (x,y) به اندازه زاویه θ اختلاف دارد (مانند شکل زیر).

معادلات دایره مور

برای به دست آوردن معادله دایره مور برای مسائل دوبعدی با تنش و کرنش صفحه‌ای، ابتدا باید یک المان دوبعدی بسیار کوچک از ماده را در اطراف نقطه P در نظر گرفت (شکل بالا). توجه داشته باشید که مساحت این المان باید در راستای موازی با صفحه yz (عمود بر صفحه‌نمایش) برابر با 1 (واحد) باشد. اگر نیروهای موجود در المان مورد نظر را در حالت تعادل در نظر بگیریم، مقدار تنش‌های نرمال σ_n و برشی τ_n با استفاده از روابط زیر به دست می‌آید:

$$\sigma _{{\mathrm {n}}}={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma_{y})\cos 2\theta +\tau _{{xy}}\sin 2\theta$$
$${\displaystyle \tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }$$

با اعمال قوانین تبدیل بر روی تانسور تنش کوشی می‌توان هر دو معادله بالا را به دست آورد.

به کارگیری این قوانین مانند استفاده از تعادل استاتیکی نیروها در راستای σ_n و τ_n است. روابط بالا، معادلات پارامتری دایره مور هستند. در این معادلات، 2θ پارامتر و σ_n و τ_n مختصات را نشان می‌دهند. به این ترتیب، با انتخاب یک نقطه بر روی دستگاه مختصات با طول σ_n و عرض τ_n و دادن مقادیر مختلف به پارامتر θ، نقاط روی دایره مشخص خواهند شد.

تعیین شعاع دایره مور

با حذف پارامتر 2θ از معادلات پارامتری بالا، معادله ناپارامتری دایره مور به دست می‌آید. اگر پس از حذف عبارات دارای پارامتر 2θ، عبارت اول در معادله اول را به سمت چپ ببریم، سپس طرفین هر دو معادله را با هم جمع کنیم، خواهیم داشت:

$${\displaystyle {\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}}$$

که در آن:

$$R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{{xy}}^{2}}}\quad {\text{}}\quad \sigma _{{\mathrm {avg}}}={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})$$

رابطه زیر، معادله یک دایره را نشان می‌دهد:

$$(x-a)^{2}+(y-b)^{2}=r^{2}$$

با مقایسه معادله بالا و معادله نا پارامتری دایره مور در سیستم مختصات (σ_n,τ_n)، می‌توان مشاهده کرد که r = R و (σ_avg,0) = (a,b) هستند.

قواعد علامت‌گذاری در دایره مور

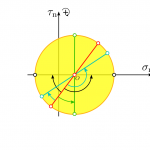
قواعد علامت‌گذاری در هنگام استفاده از دایره مور به دو دسته مجزا تقسیم می‌شوند. مجموعه اول، به منظور بررسی مؤلفه‌های تنش در فضای فیزیکی و مجموعه دوم برای ارزیابی این مؤلفه‌ها در فضای دایره مور مورد استفاده قرار می‌گیرد. این قواعد در حوزه مهندسی سازه و مکانیک با حوزه ژئومکانیک متفاوت هستند. هیچ استاندارد ثابتی برای قواعد علامت‌گذاری وجود ندارد و انتخاب هر یک از آن‌ها به سهولت محاسبات و نوع مسئله بستگی خواهد داشت. به عنوان مثال، در شکل ابتدای این بخش (مولفه‌های تنش در صفحه گذرنده از P)، قواعد علامت‌گذاری در مهندسی سازه و مکانیک به کار گرفته شده است. از این‌رو، ما نیز در این مقاله از همین قواعد استفاده می‌کنیم.

قواعد علامت‌گذاری در فضای فیزیکی

مؤلفه‌های تانسور تنش کوشی و اندیس‌های آن‌ها را در نظر بگیرید. اندیس اول، صفحه‌ای که مؤلفه مورد نظر بر روی آن اعمال می‌شود و اندیس دوم، جهت آن مؤلفه را نمایش می‌دهد. به عنوان مثال، مؤلفه τxy، در صفحه‌ای اعمال می‌شود که بردار نرمال آن در جهت مثبت محور x (اندیس اول) بوده و جهت‌گیری تنش نیز در راستای مثبت محور y (اندیس دوم) است. در قواعد علامت‌گذاری فضای فیزیکی، تنش‌های نرمالِ مثبت، به سمت بیرون المان (کشش) و تنش‌های نرمالِ منفی به سمت داخل المان (فشار) اعمال می‌شوند (شکل زیر).

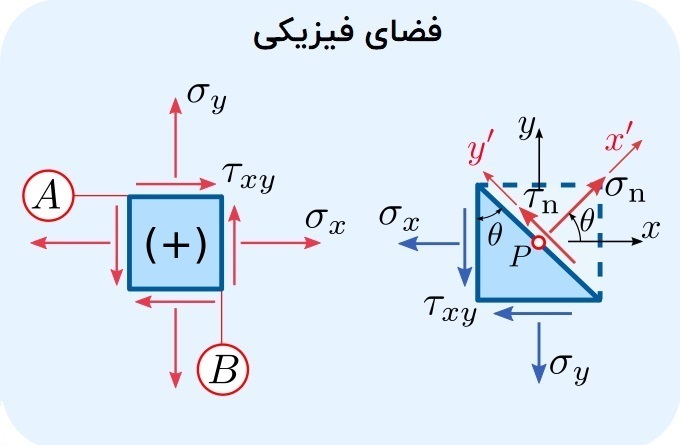
تنش‌های برشیِ مثبت بر روی صفحات مثبتِ المان جسم در جهت مثبتِ محورهای مختصات و همچنین بر روی صفحات منفیِ المان جسم در جهت منفیِ محورهای مختصات اعمال می‌شوند. بردار نرمال یک صفحه مثبت، در جهت مثبت محورهای مختصات و بردار نرمال یک صفحه منفی، در جهت منفی محورهای مختصات قرار دارد. به عنوان مثال، دلیل مثبت بودن تنش‌های برشی τ_xy و τ_yx این است که آن‌ها بر روی صفحات مثبت و در جهت مثبت محورهای x و y اعمال می‌شوند. به همین ترتیب، تنش‌های برشی متناظر با آن‌ها که طرف مقابل قرار گرفته‌اند نیز مثبت خواهند بود؛ چراکه این تنش‌ها بر روی صفحات منفی و در جهت منفی محورهای x و y عمل می‌کنند.

قواعد علامت‌گذاری در فضای دایره مور

بر اساس قواعد علامت‌گذاری در فضای دایره مور، علامت تنش‌های نرمال در این فضا با فضای فیزیکی یکسان است. به این ترتیب، تنش‌های نرمال مثبت، به سمت بیرون المان (کشش) و تنش‌های نرمال منفی به سمت داخل المان (فشار) اعمال می‌شوند.

با این وجود، قواعد علامت‌گذاری برای تنش‌های برشی در فضای دایره مور با این قواعد در فضای فیزیکی تفاوت دارند. تنش‌های برشی مثبت، در جهت خلاف عقربه‌های ساعت و تنش‌های برشی منفی، در جهت عقربه‌های ساعت اعمال می‌شوند. بر اساس این قاعده، در شکل بالا مؤلفه تنش برشی τ_xy مثبت و مؤلفه τ_yx منفی خواهد بود. برای رسم صحیح فضای دایره مور و در نتیجه رسم صحیح دایره مور، دو گزینه وجود دارد:

1. تنش‌های برشی مثبت، در سمت بالای نمودار رسم شوند (قاعده شماره 1 در شکل زیر).
2. تنش‌های برشی مثبت، در سمت پایین نمودار (با معکوس کردن محور τ_n) رسم شوند (قاعده شماره 2 در شکل زیر).

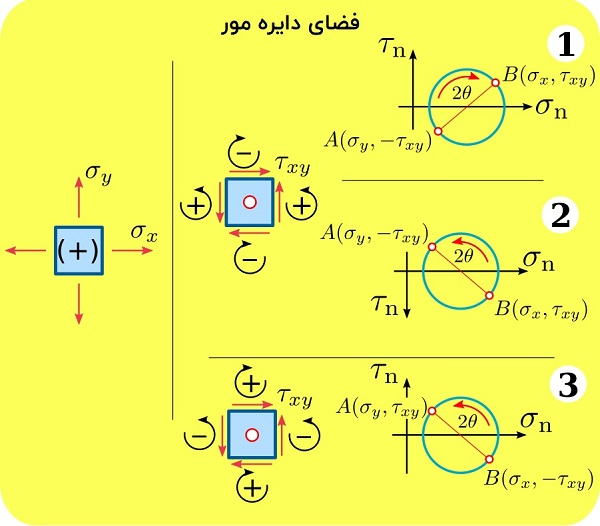
رسم تنش‌های برشیِ مثبت در بخش بالایی نمودار باعث می‌شود که زاویه 2θ بر روی دایره مور یک چرخش مثبت در جهت عقربه‌های ساعت داشته باشد. این مسئله خلاف قواعد موجود در فضای فیزیکی است. به همین دلیل، برخی ترجیح می‌دهند که تنش‌های برشی مثبت را در بخش پایینی نمودار رسم کنند. با این کار، زاویه 2θ بر روی دایره مور، یک چرخش مثبت در جهت خلاف عقربه‌های ساعت خواهد داشت. به این ترتیب، قواعد فضای دایره مور مشابه قواعد فضای فیزیکی خواهد شد.

در فضای دایره مور، یک قاعده علامت‌گذاری دیگر نیز وجود دارد. در این قاعده فرض می‌شود که تنش‌های برشی مثبت، در جهت عقربه‌های ساعت و تنش‌های برشی منفی، در جهت خلاف عقربه‌های ساعت اعمال می‌شوند (قاعده شماره 3 در شکل بالا). به علاوه، جهت رسم تنش‌های برشیِ مثبت رو به بالا است. به این ترتیب، زاویه 2θ، یک چرخش مثبت در جهت خلاف عقربه‌های ساعت دارد. در این قاعده، دایره مور مشابه دایره مور در قاعده شماره 2 خواهد بود زیرا در هر دوی آن‌ها، جهت رسم تنش‌های برشیِ مثبت به سمت بالا و جهت رسم تنش‌های برشی منفی به سمت پایین است.

توجه: در این مقاله از قاعده علامت‌گذاری در مهندسی سازه و مکانیک برای فضای فیزیکی و از قاعده شما 3 برای فضای دایره مور استفاده می‌شود.

رسم دایره مور

شکل زیر را در نظر بگیرید. بعد از اجرای تحلیل تنش، مؤلفه‌های تنش نرمال (σ_x و σ_y) و تنش برشی (τ_xy) در یک نقطه مشخص (P) به دست می‌آیند. این مؤلفه‌ها بر روی دو صفحه عمود بر هم (A و B) و گذرنده از نقطه P اعمال می‌شوند.

مختصات نقاط A و B بر روی دایره مور همان مؤلفه‌های تنش اعمال شده در صفحات A و B بر روی المان جسم هستند. برای رسم دایره مور و تعیین حالت تنش باید مراحل زیر را طی کرد:

1. رسم دستگاه مختصات کارتزین (σ, τ) با محور افقی σ_n و محور عمودی τ_n
2. تعیین محل قرارگیری دو نقطه A(σ_y, τ_xy) و B(σ_x, -τ_xy) در نمودار (σ_n, τ_n) با توجه به مؤلفه‌های تنش بر روی صفحات A و B
3. رسم یک خط مستقیم بین نقاط A و B به منظور تعیین قطر دایره مور (AB)
4. تعیین مرکز خط AB به عنوان مرکز دایره مور (این نقطه، تقاطع بین خط AB و محور σ_n است)

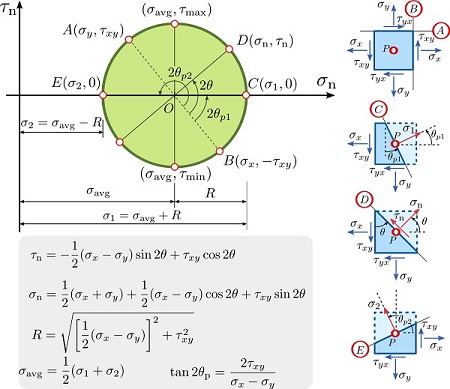
پس از رسم دایره مور، می‌توان مؤلفه‌های تنش نرمال و برشی در جهات دلخواه را به دست آورد. در ادامه به نحوه تعیین مؤلفه‌های تنش با استفاده از دایره مور می‌پردازیم.

تعیین تنش‌های نرمال اصلی با استفاده از دایره مور

در شکل بالا، نقاط C و E را در نظر بگیرید. طول این نقاط بر روی محور افقی (تقاطع دایره با محور σ_n)، مقدار تنش‌های اصلی را نشان می‌دهد. مقدار تنش اصلی بزرگ (σ₁)، همیشه نقطه‌ای است که قدر مطلق آن بزرگ‌تر و مقدار تنش اصلی کوچک (σ₂)، همیشه نقطه‌ای است که قدر مطلق آن کوچک‌تر باشد. همان طور که انتظار می‌رود، مختصات این دو نقطه نسبت به محور تنش برشی صفر است (همانند مؤلفه‌های تنش برشی در صفحات اصلی). برای تعیین مقادیر تنش‌های اصلی می‌توان از روابط زیر نیز استفاده کرد:

$$\sigma _{1}=\sigma _{\max }=\sigma _{{\text{avg}}}+R$$

$$\sigma _{2}=\sigma _{\min }=\sigma _{{\text{avg}}}-R$$

σ_avg در معادلات بالا بر روی مرکز دایره قرار دارد:

$$\sigma _{{\text{avg}}}={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})$$

طول شعاع دایره (R) نیز طبق معادله دایره گذرنده از دو نقطه برابر است با:

$$R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{{xy}}^{2}}}$$

تعیین تنش‌های برشی مینیمم و ماکسیمم با استفاده از دایره مور

تنش‌های برشی مینیمم و ماکسیمم به ترتیب با بالاترین و پایین‌ترین نقاط دایره در ارتباط هستند. هر یک از این نقاط بر روی تقاطع دایره با خط عمودی گذرنده از مرکز دایره (O) قرار گرفته است. بنابراین، مقدار تنش‌های برشی مینیمم و ماکسیمم با شعاع دایره برابر خواهد بود:

$$\tau _{{\max ,\min }}=\pm R$$

تعیین مؤلفه‌های تنش در یک صفحه دلخواه با استفاده از دایره مور

همان طور که پیش از این نیز اشاره شد، پس از اجرای تحلیل‌های تنش دوبعدی می‌توان مقادیر مؤلفه‌های تنش نرمال (σ_x و σ_y) و تنش برشی (τ_xy) را در نقطه P به دست آورد. این مؤلفه‌ها بر روی دو صفحه عمود بر هم (A و B) اعمال می‌شوند. صفحات A و B از نقطه P می‌گذرند. کاربرد دایره مور، تعیین مؤلفه‌های تنش σ_n و τ_n در هر نقطه دلخواه بر روی دایره است. برای این منظور، دو رویکرد «زاویه مضاعف» (Double Angle) و «قطب صفحات» (Pole of Planes) مورد استفاده قرار می‌گیرند.

زاویه مضاعف

شکل پایین را در نظر بگیرید. برای تعیین مؤلفه‌های تنش (σ_n, τ_n) اعمال شده بر روی صفحه D، باید به اندازه 2θ در جهت خلاف عقربه‌های ساعت از نقطه مشخص B(σx, -τ_xy) به نقطه D(σ_n, τ_n) بر روی دایره حرکت کنیم. 2θ همان زاویه بین دو خط OB و OD در دایره مور است.

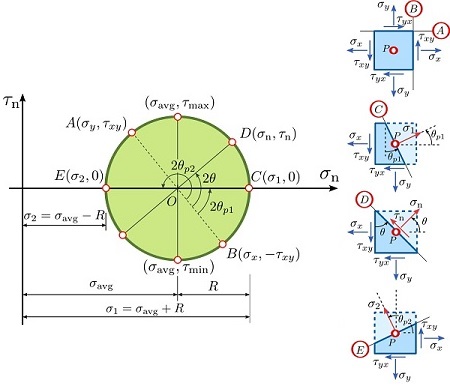
رویکرد زاویه مضاف بر اساس این واقعیت بنا شده است که زاویه θ بین بردارهای نرمال دو صفحه فیزیکی دلخواه و گذرنده از نقطه P، نصف زاویه بین دو خط اتصال‌دهنده نقاط تنش آن‌ها به مرکز دایره است. معادلات پارامتری دایره مور، تابعی از 2θ هستند و رابطه زاویه مضاعف نیز از همین واقعیت تبعیت می‌کند. به علاوه، می‌توان مشاهده کرد که زاویه بین دو صفحه A و B در المان دربرگیرنده نقطه P برابر با ^∘θ=90 و در دایره مور برابر با ^∘θ=180 (زاویه مضاعف) است.

مبدأ یا قطب صفحات

رویکرد دومی که برای تعیین یک نقطه بر روی دایره مور مورد استفاده قرار می‌گیرد، مبدأ یا قطب صفحات نام دارد. هر خط مستقیمی که از قطب رسم شود و با دایره مور تقاطع داشته باشد، معرف حالت تنش بر روی صفحه‌ای با جهت‌گیری مشابه (موازی) با آن خط خواهد بود. بنابراین، با دانستن مؤلفه‌های σ و τ بر روی یک صفحه دلخواه و رسم یک خط موازی با آن صفحه در دستگاه مختصات (σ_n,τ_n)، قطب مورد نظر در محل تقاطع خط و دایره مور به دست می‌آید.

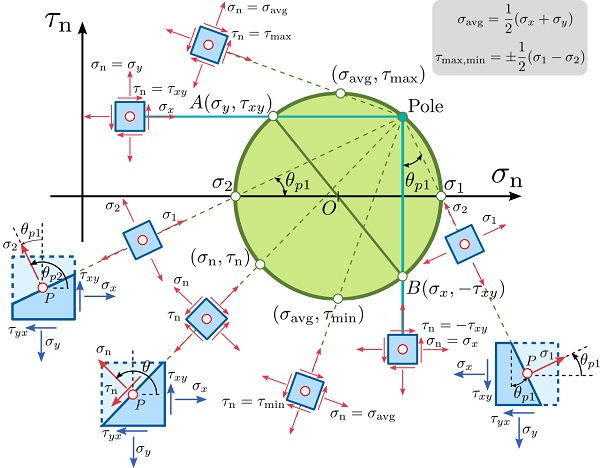
به عنوان مثال، تصویر بالا را در نظر بگیرید. بر اساس این تصویر، یک حالت تنش با مؤلفه‌های σ_y ،σ_x و τ_xy داریم (در نقاط A و B). برای تعیین قطب می‌توانیم یک خط از نقطه B موازی با صفحه اعمال σ_x یا یک خط از نقطه A موازی با صفحه اعمال σ_y رسم کنیم. تقاطع هر یک از این خط‌ها با دایره مور، محل قرارگیری قطب خواهد بود. پس از مشخص کردن قطب، می‌توانیم حالت تنش بر روی صفحه‌ای با زاویه θ نسبت به محور قائم یا به عبارت دیگر، صفحه‌ای که بردار نرمال آن نسبت به افق زاویه θ می‌سازد را تعیین کنیم. به این منظور تنها باید خطی را از قطب به صورت موازی با صفحه مذکور رسم کنیم. مختصات محل تقاطع خط با دایره مور، تنش‌های نرمال و برشی بر روی آن صفحه را نشان می‌دهند.

تعیین جهت صفحات اصلی با استفاده از دایره مور

«صفحات اصلی» (Principal Planes)، صفحاتی هستند که تنش‌های اصلی مینیمم و ماکسیمم بر روی آن‌ها رخ می‌دهند. شکل زیر را در نظر بگیرید. با تعیین نصف زوایای BOC و BOE در دایره مور، جهت‌گیری هر یک از صفحات اصلی به دست می‌آید. بنابراین، زاویه BOC دو برابر زاویه‌ای است که صفحه اعمال تنش اصلی بزرگ با صفحه B می‌سازد (θ_p).

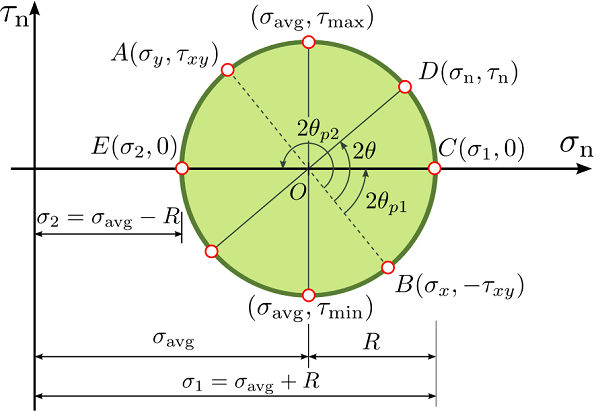
زوایای θ_p1 و θ_p2 را می‌توان از طریق رابطه زیر نیز به دست آورد:

$$\tan 2\theta _{{\mathrm {p}}}={\frac {2\tau _{{xy}}}{\sigma _{x}-\sigma _{y}}}$$

با استفاده از معادله بالا، دو مقدار برای θ_p به دست می‌آید که با هم 90 درجه اختلاف دارند. اگر مقدار تنش برشی (τ_n) در معادله پارامتری دایره مور را برابر با صفر قرار دهیم به معادله بالا خواهیم رسید زیرا مقدار تنش برشی در صفحات اصلی همیشه برابر با صفر است. در ادامه، برای درک بهتر فرآیند تعیین مؤلفه‌های مختلف تنش با استفاده از دایره مور، یک مثال را برای شما حل خواهیم کرد.

نمونه‌ای از کاربرد دایره مور در تعیین مؤلفه‌های تنش

یک المان جسم و حالت تنش اعمال شده به آن را مطابق شکل‌ زیر را در نظر بگیرید. همان طور که مشاهده می‌کنید، این المان نسبت به صفحه افقی 10 درجه اختلاف دارد.

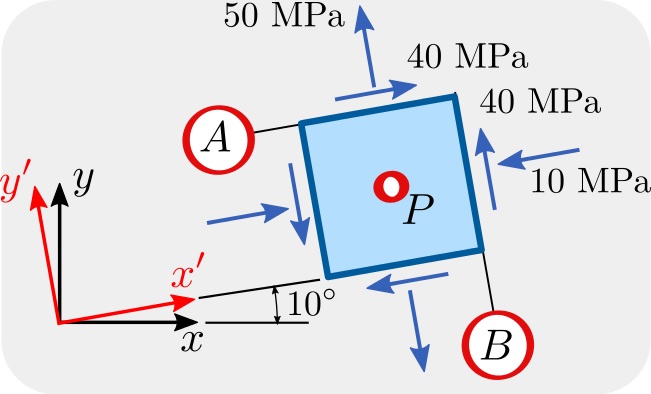
در این مثال، می‌خواهیم با استفاده از دایره مور، پارامترهای زیر را به دست بیاوریم:

• راستای صفحاتی که تنش بر روی آن اعمال شده است
• تنش‌های برشی ماکسیمم و راستای صفحاتی که بر روی آن‌ها اعمال می‌شوند
• مؤلفه‌های تنش در یک صفحه افقی

راه حل:

مرحله اول در حل این مسئله، تعیین علامت تنش‌های مشخص است. بر اساس قواعد علامت‌گذاری در مهندسی سازه و مکانیک برای فضای فیزیکی (بخش‌های قبلی)، علامت و مقدار مؤلفه‌های تنش برای این المان به صورت زیر خواهد بود:

$$\sigma _{{x'}}=-10{\textrm {MPa}}$$

$$\sigma _{{y'}}=50{\textrm {MPa}}$$

$$\tau _{x'y'}=40{\textrm {MPa}}$$

در مرحله بعد، باید دایره مور برای این حالت تنش بخصوص رسم شود. به این منظور، یک دستگاه مختصات کارتزین (σ_n,τ_n) را رسم می‌کنیم که مقادیر مثبت τ_n در آن در بخش بالایی نمودار قرار دارند. سپس، نقاط A(50, 40) و B(-10, -40) را بر روی دستگاه مختصات تعیین می‌کنیم. این نقاط، وضعیت تنش در صفحات A و B را نشان می‌دهند. به منظور تعیین علامت تنش‌های اعمال شده به این نقاط، از قواعد علامت‌گذاری در مهندسی سازه و مکانیک برای فضای دایره مور استفاده می‌شود. بر اساس این قواعد، جهت تنش‌های نرمالِ مثبت باید به سمت بیرون المان و جهت تنش‌های برشیِ مثبت در جهت عقربه‌های ساعت باشند. در این مثال، تنش برشی اعمال شده بر صفحه B منفی و تنش برشی اعمال شده بر صفحه A مثبت خواهد بود. با اتصال نقاط A و B به یکدیگر، قطر دایره به دست می‌آید و تقاطع این قطر با محور σ_n، مرکز دایره را نشان می‌دهد. با مشخص شدن مرکز دایره و طول قطر آن، می‌توانیم دایره مور برای این حالت تنش بخصوص را رسم کنیم (شکل زیر).

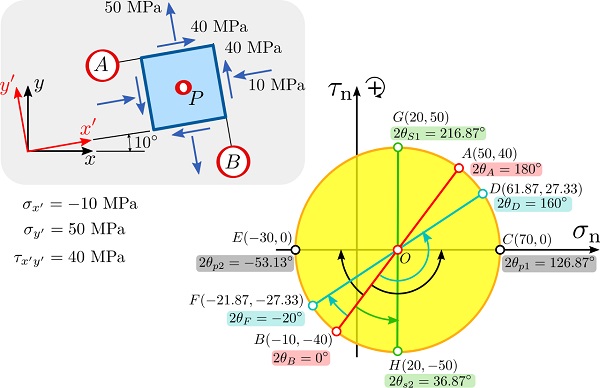
تقاطع محور σ_n با دایره مور در نقاط E و C، مقادیر تنش‌های نرمال مینیمم و ماکسیمم را نشان می‌دهد. در مختصات هر دوی این نقاط، مقادیر تنش‌های برشی اعمال شده به صفحات اصلی کوچک و بزرگ مشخص است. همان طور که می‌دانید، این مقادیر در صفحات اصلی برابر با صفر خواهند بود.

با اینکه ایده اصلی دایره مور، به کارگیری آن در تعیین مؤلفه‌های تنش با استفاده از اندازه‌گیری مختصات مختلف بر روی دایره است، برای اطمینان از نتایج پیشنهاد می‌شود از روش‌های تحلیلی نیز کمک گرفته شود. به این ترتیب، اندازه مرکز دایره و طول آن بر روی محور مختصات به صورت زیر به دست می‌آید:

$${\begin{aligned}R&={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\\&={\sqrt {\left[{\tfrac {1}{2}}(-10-50)\right]^{2}+40^{2}}}\\&=50{\textrm {MPa}}\\\end{aligned}}$$

$${\begin{aligned}\sigma _{\mathrm {avg} }&={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\\&={\tfrac {1}{2}}(-10+50)\\&=20{\textrm {MPa}}\\\end{aligned}}$$

برای مقادیر تنش‌های اصلی نیز داریم:

$${\begin{aligned}\sigma _{1}&=\sigma _{{\mathrm {avg}}}+R=70{\textrm {MPa}}\end{aligned}}$$

$${\begin{aligned}\sigma _{2}&=\sigma _{{\mathrm {avg}}}-R=-30{\textrm {MPa}}\end{aligned}}$$

مختصات نقاط H و G بر روی دایره مور، مقادیر تنش‌های برشی مینیمم و ماکسیمم را نشان می‌دهند. طول نقاط H و G، مقدار تنش‌های نرمالی که بر روی صفحات تنش‌های برشی مینیمم و ماکسیمم اعمال می‌شوند را مشخص می‌کند. مقادیر تنش‌های برشی مینیمم و ماکسیمم به صورت زیر نیز قابل محاسبه است:

$$\tau _{{\max,\min }}=\pm R=\pm 50{\textrm {MPa}}$$

مقدار تنش‌های نرمال موجود در صفحات اعمال، برابر با σ_avg است.

برای تعیین جهت تنش‌های نرمال و برشی اصلی می‌توان از روش‌های زاویه مضاعف یا قطب صفحات استفاده کرد. در رویکرد زاویه مضاعف، به منظور یافتن دو برابر زاویه‌ای که تنش برشی بزرگ و تنش اصلی کوچک با صفحه B در فضای فیزیکی می‌سازند، زوایای BOC و BOE در دایره مور را اندازه‌گیری می‌کنیم. برای تعیین دقیق مقادیر این زوایا می‌توانیم به جای محاسبه گرافیکی، از روابط تحلیلی نیز بهره ببریم:

$${\begin{aligned}2\theta _{\mathrm {p} }=\arctan {\frac {2\tau _{xy}}{\sigma _{x}-\sigma_{y}}} = \arctan{\frac {2*40}{(-10-50)}}= -\arctan {\frac{4}{3}}\end{aligned}}$$

یکی از جواب‌ها ^◦2θ_p=-53.13 است. با بررسی شکل اول می‌توان دریافت که این زاویه به زاویه BOE مربوط می‌شود. بنابراین، برای زاویه اصلی کوچک داریم:

$$\theta _{{p2}}=-26.565^{\circ }$$

به این ترتیب، زاویه اصلی بزرگ به صورت زیر به دست خواهد آمد:

$${\begin{aligned}2\theta _{{p1}}&=180-53.13^{\circ }=126.87^{\circ }\\\theta _{{p1}}&=63.435^{\circ }\\\end{aligned}}$$

به خاطر داشته باشید که در این مثال بخصوص، زوایای θ_p1 و θ_p2 نسبت به صفحه اعمال تنش _′σ_x (در جهت محور ′x) تعیین شده‌اند و محاسبه آن‌ها نسب به صفحه اعمال تنش σ_x (در جهت محور x) نبوده است.

در رویکرد قطب صفحات، ابتدا مبدأ یا قطب صفحات تعیین می‌شود. به این منظور، از نقطه A بر روی دایره مور خطی با زاویه 10 درجه نسبت به افق رسم می‌کنیم. این خط، موازی با صفحه‌ای است که ′σ_y بر روی آن اعمال می‌شود (صفحه A). تقاطع خط رسم شده با دایره مور، قطب مورد نظر ما را نشان خواهد داد. برای اطمینان از محل قرارگیری قطب، از نقطه B موازی با صفحه‌ای که ′σ_x بر روی آن اعمال می‌شود (صفحه B) خطی را رسم می‌کنیم. تقاطع دایره مور با این خط باید با محل تقاطع قبلی یکسان باشد.

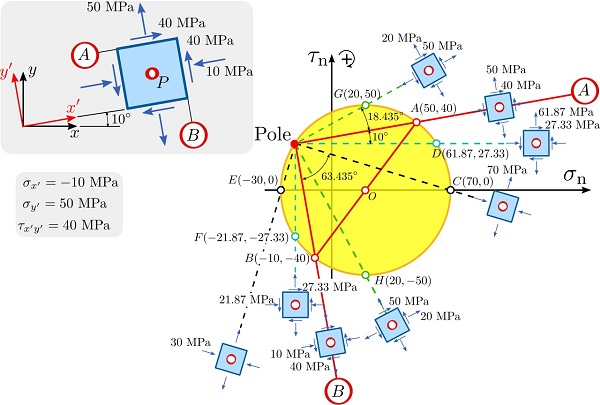
از قطب به نقاط مختلف بر روی دایره مور، چند خط رسم می‌کنیم. مختصات تقاطع این خطوط با دایره مور، مؤلفه‌های تنش اعمال شده بر صفحاتی در فضای فیزیکی را نشان می‌دهد که دارای شیبی برابر با شیب این خطوط رسم شده هستند. به عنوان مثال، خطی که قطب را به نقطه C بر روی دایره متصل می‌کند، هم‌شیب با صفحه‌ای است که تنش σ₁ در آن اعمال می‌شود. این صفحه، هم در فضای دایره مور و هم در فضای فیزیکی، 63.435 درجه با صفحه B اختلاف دارد. در شکل بالا، خطوط دیگری نیز از قطب به نقاط G ،F ،E ،D و H برای تعیین مؤلفه‌های تنش بر روی صفحاتی با راستای مشابه رسم شده‌اند.

تعیین حالت کلی تنش در سه بعد

برای رسم دایره مور و تعیین حالت کلی تنش‌های یک نقطه در سه بعد، ابتدا باید مقادیر تنش‌های اصلی (σ₁, σ₂, σ₃) و جهات اصلی (n₁, n₂, n₃) برای هر یک از آن‌ها را محاسبه کرد.

با در نظر گرفتن جهات اصلی به عنوان دستگاه مختصات (به جای x₁, x₂, x₃) و با فرض σ₁ > σ₂ > σ₃، مقادیر مؤلفه‌های نرمال و برشیِ بردار تنش (T⁽ⁿ⁾) برای صفحه‌ای با بردار یکه n، از معادلات زیر پیروی خواهند کرد:

$${\begin{aligned}\left(T^{{(n)}}\right)^{2}&=\sigma _{{ij}}\sigma _{{ik}}n_{j}n_{k}\end{aligned}}$$

$$\begin{aligned}\sigma _{{\mathrm {n}}}^{2}+\tau _{{\mathrm {n}}}^{2}&=\sigma _{1}^{2}n_{1}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{3}^{2}\end{aligned}$$

$${\sigma _{\mathrm {n} } = \sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}.} \sigma _{{\mathrm {n}}} = \sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}$$

با دانستن رابطه زیر:

$${\displaystyle n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1} n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1$$

می‌توانیم معادلات قبلی را با استفاده از روش حذف گاوسی برای به دست آوردن مقادیر ²(n_i) به کار بگیریم:

$${\begin{aligned}n_{1}^{2}&={\frac {\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{2})(\sigma _{{\mathrm {n}}}-\sigma _{3})}{(\sigma _{1}-\sigma _{2})(\sigma _{1}-\sigma _{3})}}\geq 0\\n_{2}^{2}&={\frac {\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{3})(\sigma _{{\mathrm {n}}}-\sigma _{1})}{(\sigma _{2}-\sigma _{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{1})(\sigma _{{\mathrm {n}}}-\sigma _{2})}{(\sigma _{3}-\sigma _{1})(\sigma _{3}-\sigma _{2})}}\geq 0\end{aligned}}$$

از آنجایی که σ₁ > σ₂ > σ₃ و ²(n_i) مقداری غیر منفی است، شرط‌های زیر برای معادلات بالا صادق خواهد بود:

$$\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{2})(\sigma _{{\mathrm {n}}}-\sigma _{3})\geq 0,\ \ {\sigma _{1}-\sigma _{2}>0,}\ \ {\sigma _{1}-\sigma _{3}>0}$$

$$\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{3})(\sigma _{{\mathrm {n}}}-\sigma _{1})\geq 0,\ \ {\sigma _{2}-\sigma _{3}>0,}\ \ {\sigma _{2}-\sigma _{1}>0}$$

$$\tau _{{\mathrm {n}}}^{2}+(\sigma _{{\mathrm {n}}}-\sigma _{1})(\sigma _{{\mathrm {n}}}-\sigma _{2})\geq 0,\ \ {\sigma _{3}-\sigma _{1}>0,}\ \ {\sigma _{3}-\sigma _{2}>0}$$

معادلات بالا را می‌توان به صورت زیر بازنویسی کرد:

$${\begin{aligned}\tau _{{\mathrm {n}}}^{2}+\left[\sigma _{{\mathrm {n}}}-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{{\mathrm {n}}}^{2}+\left[\sigma _{{\mathrm {n}}}-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{{\mathrm {n}}}^{2}+\left[\sigma _{{\mathrm {n}}}-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}$$

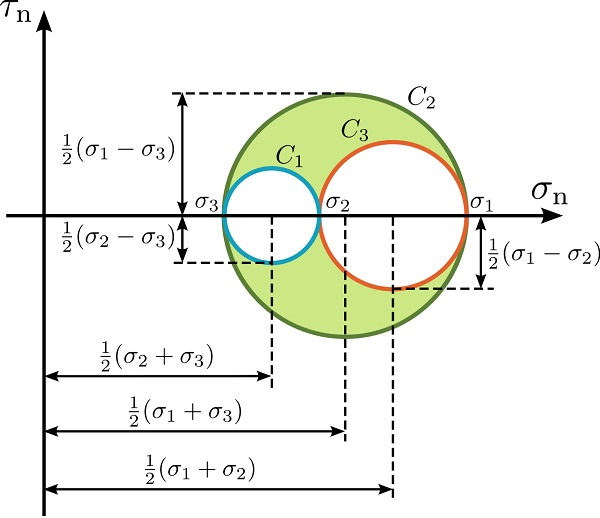
این روابط، معادلات دایره مور برای تنش‌های C₂ ،C₁ و C₃ با شعاع‌های زیر هستند:

$${\displaystyle R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})}$$

$${\displaystyle R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})}$$

$${\displaystyle R_{3}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})}$$

مختصات مرکز هر یک از این دوایر، به ترتیب به صورت زیر به دست می‌آید:

$${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]}$$

$${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]}$$

$${\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]}$$

این معادلات، تمام نقاط قابل قبول تنش (σ_n,τ_n) بر روی دوایر یا نواحی محصور شده توسط آن‌ها را مشخص می‌کنند (نواحی رنگی در شکل زیر).

نقاط قابل قبول تنش برای معادله دایره C₁، بر روی C₁ یا بیرون آن قرار می‌گیرند. نقاط قابل قبول تنش برای معادله دایره C₂، بر روی C₂ یا داخل آن قرار می‌گیرند. در نهایت، نقاط قابل قبول تنش برای معادله دایره C₃، بر روی C₃ یا بیرون آن قرار می‌گیرند.

امیدواریم این مقاله برایتان مفید واقع شده باشد.اگر به مطالعه موضوعات مشابه علاقه‌مند هستید، مطالب زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش های مهندسی عمران
• آموزش مقاومت مصالح
• مجموعه آموزش‌های دروس مهندسی مکانیک
• آموزش تنش و کرنش بارگذاری محوری در مقاومت مصالح
• آشنایی با دایره مور به زبان ساده
• مجموعه مقالات آشنایی با مفاهیم مقاومت مصالح و خواص مکانیکی مواد

^^