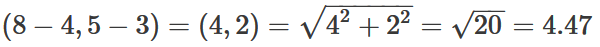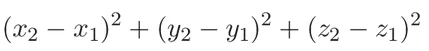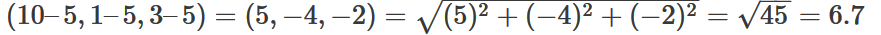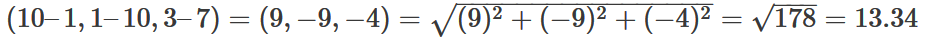اندازه گیری مسافت ها با قضیه فیثاغورس – به زبان ساده

ما همواره قضیه فیثاغورس را دست‌کم می‌گیریم. تصور می‌کنیم این قضیه صرفاً در مورد مثلث‌ها است در حالی که در مورد هر شکلی صدق می‌کند. قضیه فیثاغورس در مورد a، b و c نیست؛ بلکه در مورد هر فرمولی که عبارت درجه دوم دارد به کار می‌رود.

منظور ما از مسافت در عنوان این نوشته حرکت در راستای قطر در یک اتاق مربعی نیست؛ بلکه شامل هر نوع مسافتی مثلاً فاصله بین ترجیح‌های فیلم یا اولویت‌های رنگی ما نیز می‌شود. اگر چیزی را بتوان اندازه‌گیری کرد در این صورت می‌توان آن را با قضیه فیثاغورس مقایسه نمود.

درک قضیه

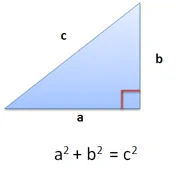
می‌دانیم که قضیه فیثاغورس صحیح است. در هر مثلث قائم‌الزاویه:

اگر a=3 و b=4 در این صورت c=5 خواهد بود.

یک مشاهده کلیدی در این زمینه آن است که a و b زوایای قائمه هستند. حرکت در یک جهت تأثیری بر دیگری ندارد. این مسئله تا حدودی شبیه شمال/جنوب در برابر شرق/غرب است. حرکت به سمت شمال تغییری در جهت‌گیری غرب/شرق شما ایجاد نمی‌کند و برعکس. جهت‌ها مستقل از هم هستند و اصطلاح تخصصی آن «متعامد» است.

قضیه فیثاغورس امکان یافتن کوتاه‌ترین مسیر بین جهت‌های متعامد را به ما می‌دهد. بنابراین شاید واقعاً به مثلث‌های قائم‌الزاویه مربوط نباشد؛ بلکه در مورد مقایسه چیزهایی باشد که در زوایای قائمه حرکت می‌کنند.

برای مثال اگر 3 واحد به سمت شرق و 4 واحد به سمت شمال حرکت کنید، چه مقدار از نقطه آغاز فاصله گرفته‌اید؟ پاسخ این است که 5 واحد فاصله گرفته‌ایم.

شاید از خود بپرسید پس در مورد c چه می‌توان گفت؟ c را می‌توان تنها یک عدد تصور کرد؛ اما بدین ترتیب در همان اقلیم ملال‌آور مثلث‌ها باقی می‌مانیم. می‌توان c را نوعی ترکیب a و b دانست.

اما این ترکیب چیز ساده‌ای مثل جمع نیست، چون در هر حال c برابر با a+b نیست. قضیه فیثاغورس به ما امکان می‌دهد، مؤلفه‌های متعامد را به روشی مانند جمع با هم ترکیب کنیم و نکته مهم همین جا است.

در مثال ما c 5 واحد مسافت را تشکیل می‌دهد. اما در واقعیت چیزی بیش از این است. در واقع c ترکیبی از 3 واحد شرقی و 4 واحد شمالی است. حرکت در راستای c به معنی حرکت همزمان در جهت‌های شمال و شرق است. این روش جالبی برای تفکر در مورد این قضیه است.

زنجیره‌سازی قضیه

در این بخش می‌خواهیم ببینیم در صورت زنجیره‌سازی دو قضیه فیثاغورس با هم چه اتفاقی می‌افتد؟

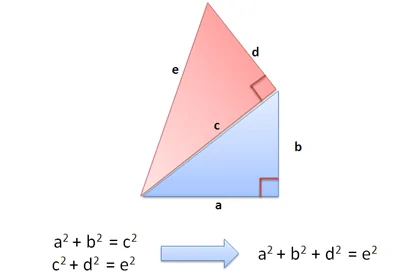
نتیجه جالبی است. ما مثلث قرمز دیگری را روی ضلع c اضافه کردیم. از آنجا که c و d در زوایای قائمه هستند (متعامد)، رابطه فیثاغورسی زیر را به دست می‌آوریم:

c² + d² = e²

و اگر جای c2 را با a2 + b2 عوض کنیم، رابطه زیر را به دست می‌آوریم:

a² + b² + d² = e²

یعنی ما e را بر حسب مؤلفه متعامد a، b و d نوشته‌ایم.

بسط به فضای سه‌بعدی

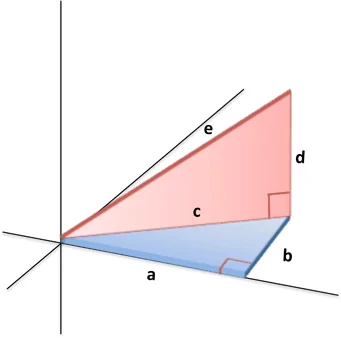
اگر فکر می‌کنید دو مثلث فوق عجیب هستند. سعی کنید این دو مثلث را از کاغذ برش دهید. حال به جای این که آن‌ها با به صورت مسطح کنار هم قرار دهید، مثلث قرمز را به صورت قائم روی وتر مثلث آبی قرار دهید.

این وضعیت نیز به اندازه نتیجه قبلی عجیب است. ما صرفاً از زاویه دیگری به آن نگاه می‌کنیم. اما اینک در فضای 3 بُعدی قرار داریم. اگر اضلاع مثلث را به جای a، b و d به صورت x، y و z بنامیم و اگر مسافت را با عبارت dis نشان دهیم، در این صورت داریم:

x² + y² + z² = (dis)²

نتیجه جالبی است. ما در ریاضیات معمولاً مختصات x (فاصله از چپ/راست)، مختصات y (فاصله از جلو/عقب) و مختصات z (فاصله از بالا/پایین) را اندازه‌گیری می‌کنیم. اینک می‌توانیم مسافت 3 بعدی از یک نقطه مفروض را با استفاده از مختصاتش به دست آوریم.

استفاده از هر نوع ابعاد

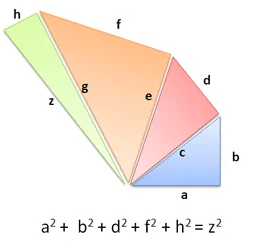
همان طور که احتمالاً حدس می‌زنید تعمیم قضیه فیثاغورس را می‌توان در مورد هر تعداد ابعاد مورد استفاده قرار داد. یعنی شما می‌توانید هر تعداد مثلث که می‌خواهید را روی وترهای همدیگر ترسیم کنید:

می‌توانید تصور کنید که هر مثلث بعد خاص خود را دارد. اگر هر قطعه به صورت زاویه قائمه باشد، قضیه صدق می‌کند و می‌توان از آن استفاده کرد.

مسافت چگونه محاسبه می‌شود؟

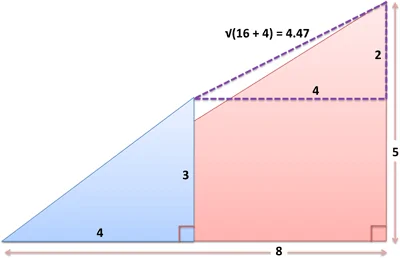
قضیه فیثاغورس مبنای محاسبه مسافت بین دو نقطه است. دو مثلث زیر را در نظر بگیرید:

• مثلثی با اضلاع 4 و 3 (آبی)
• مثلثی با اضلاع 8 و 5 (صورتی)

از رأس مثلث آبی در مختصات (4,3) تا رأس مثلث صورتی در مختصات (8,5) چه مسافتی است؟ می‌توان یک مثلث مجازی بین دو نقطه ایجاد کرد. وتر این مثلث فرضی مسافت بین دو نقطه را تعیین می‌کند:

در محیط 3 بعدی نیز فاصله بین دو نقطه (x1,y1,z1) و (x2,y2,z2) را می‌توان با استفاده همین رویکرد یافت:

مهم نیست که یک ضلع از دیگری بزرگ‌تر باشد، چون اختلاف آن دو زمانی که به توان 2 برسد مثبت خواهد شد.

چگونه از هر مسافتی استفاده کنیم؟

باید توجه داشته باشید که قضیه فیثاغورس محدود به تعریف مقیدی که ما ارائه کردیم نمی‌شود. این قضیه در مورد هر مسافت متعامدی در مورد فضا، زمان، فیلم، رنگ، دما و غیره می‌شود. در واقع از این قضیه می‌توان در مورد هر مجموعه‌ای از اعداد (a,b,c,d,e) استفاده کرد.

اندازه‌گیری ترجیح‌های کاربران

فرض کنید یک پیمایش در مورد ترجیح‌های فیلم کاربران اجرا کرده‌ایم:

• فیلم رمبو (فیلم اکشن) را چه قدر دوست داشتید؟ (1 تا 10)
• فیلم بامبی (انیمیشن کودکان) را چقدر دوست داشتید؟ (1 تا 10)
• سریال سینفیلد (درام خانوادگی) را چه قدر دوست داشتید؟ (1 تا 10)

اینک امتیازهای افراد را چگونه می‌توانیم مقایسه کنیم؟ چگونه می‌توان ترجیح‌های مشابه را یافت؟ چاره کار قضیه فیثاغورس است.

اگر ترجیح‌ها را به صورت نقاطی (رمبو، بامبی، سینفیلد) در نظر بگیریم، می‌توانیم پاسخ‌های پیمایش خود را به صورت زیر نمایش دهیم:

• روحیه سخت: (10, 1, 3)
• روحیه متوسط: (5, 5, 5)
• روحیه ظریف: (1,10, 7)

و با استفاده از قضیه فیثاغورس می‌توان تفاوت بین افراد مختلف را ببینیم:

فاصله روحیه سخت تا روحیه متوسط:

فاصله روحیه سخت تا روحیه ظریف:

اگر مسافت را با عبارت dis نشان دهیم، این مسافت‌ها را با استفاده از نسخه زیر:

a² + b² + c² = (dis) ²

نیز می‌توان محاسبه کرد. همان طور که انتظار داریم بین روحیه سخت و ظریف نسبت به روحیه متوسط که در میانه قرار دارد، اختلاف بیشتری مشاهده می‌شود. این قضیه به ما کمک می‌کند که این مسافت را به صورت کمّی محاسبه کنیم و کارهای جالبی مانند خوشه‌بندی نتایج مشابه انجام دهیم.

این تکنیک می‌تواند در رتبه‌بندی ترجیح‌های فیلم نتفلیکس و دیگر انواع فیلترینگ جمعی که تلاش می‌شود بر اساس ترجیح‌ها برخی تصمیم‌گیری‌ها صورت بگیرد قابل استفاده است. به بیان فنی، ما ترجیح‌ها را به صورت بُرداری نمایش دادیم و از قضیه فیثاغورس برای یافتن مسافت بین آن‌ها و احتمالاً گروه‌بندی‌شان استفاده کردیم.

یافتن مسافت رنگی

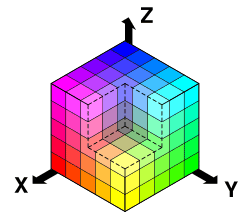
اندازه‌گیری مسافت بین رنگ‌ها یکی دیگر از کاربردهای مفید این قضیه است. رنگ‌ها معمولاً به صورت مقادیر قرمز/سبز/آبی (RGB) از کمترین مقدار 0 تا بیشترین مقدار 255 نمایش می‌یابند. برای نمونه:

• سیاه: (0, 0, 0) – فاقد رنگ
• سفید: (255, 255, 255) - بیشینه هر رنگ
• قرمز: (0, 0, 255) – قرمز خالص و فاقد هر رنگ دیگر.

ما می‌توانیم همه رنگ‌ها را در یک «فضای رنگ» مانند زیر نمایش دهیم:

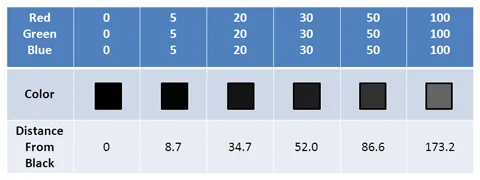
ما می‌توانیم فاصله بین رنگ‌ها را به روش معمول خود محاسبه کنیم، یعنی فاصله مقادیر قرمز/سبز/آبی را از رنگ سیاه (0, 0, 0) محاسبه کنیم. به نظر می‌رسد که چشم انسان قدرت تشخیص بین رنگ‌های با فاصله 4 واحد از هم را ندارد. حتی رنگ‌هایی که از همدیگر 30 واحد فاصله دارند، هم بسیار شبیه هم هستند.

همه این محاسبات مسافت شبیه هم هستند. مسافت رنگ به ما مقیاسی کمی برای اندازه‌گیری میزان اختلاف بین رنگ‌ها می‌دهد.

هر چیزی را می‌توان اندازه‌گیری کرد

اگر بتوانید مجموعه‌ای از خصوصیات را با اعداد نمایش دهید، آنگاه می‌توانید آن‌ها را با استفاده از قضیه فیثاغورس مقایسه کنید:

فیلم آموزش حل مسائل ریاضی دبیرستان با نرم افزار میپل Maple در فرادرس

کلیک کنید

• دما در طی هفته: (شنبه، یکشنبه، دوشنبه، سه‌شنبه، چهارشنبه). دمای هفته‌های متوالی را مقایسه کنید تا ببینید میزان تغییرات چه مقدار است؟
• تعداد مشتریانی که هر ساعت، هر روز یا هر هفته به فروشگاه مراجعه می‌کنند.
• مسافت فضا-زمان (طول، عرض، ارتفاع، تاریخ). این محاسبات در صورتی که بخواهید یک ماشین زمان یا دست‌کم یک بازی ویدئویی در مورد آن بسازید، مفید خواهند بود.
• تفاوت بین افراد: (قد، وزن، سن)
• تفاوت بین شرکت‌ها: (درآمد، سود، حجم بازار)

شما حتی می‌توانید با تغییر وزن هر یک از خصوصیت‌ها، مسافت‌ها را به روش متفاوتی محاسبه کنید و مثلاً اختلاف سنی را در یک عامل معینی ضرب کنید. اما ایده اصلی چنان مهم است که باید یک بار دیگر آن را تکرار کنیم: اگر شما بتوانید چیزی را کمّی‌سازی کنید در این صورت می‌توانید آن را با استفاده از قضیه فیثاغورس مقایسه کنید.

محورهای x، y و z شما می‌توانند هر کمیتی را نشان دهند. شما محدود به 3 بُعد نیستید. البته ریاضیدان‌ها دوست دارند که شما را با روش‌های دیگر اندازه‌گیری مسافت (مانند فضای متریک) آشنا کنند؛ اما قضیه فیثاغورس بسیار مشهور است و نقطه شروع خوبی محسوب می‌شود.

سخن پایانی

اگر مفاهیمی که در این نوشته معرفی شدند را یک بار دیگر ملاحظه کنید، می‌بینید که موارد زیادی هستند که باید بیاموزید. ریاضیات زیبا است؛ اما این ظرافت ریاضیات معمولاً زیر اثبات‌های مکانیکی و کوهی از معادلات مدفون می‌شود. ما به اثبات‌های بیشتر نیاز نداریم؛ بلکه باید نتایج جذاب و شهودی به دست آوریم.

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

برای نمونه قضیه فیثاغورس را در موارد زیر بررسی کنید:

• آیا قضیه فیثاغورس در مورد هر شکلی به جز مثلث (مثلاً دایره) نیز صدق می‌کند؟
• آیا قضیه فیثاغورس برای هر معادله‌ای که جمله درجه دوم دارد (مثلاً 1/2 mv² ) صدق می‌کند؟
• آیا قضیه فیثاغورس در مورد هر تعداد از ابعاد (مثلاً) صدق می‌کند؟
• آیا قضیه فیثاغورس هر مسافتی (مثلاً بین رنگ‌ها یا فیلم‌های مختلف) را اندازه‌گیری می‌کند؟

می‌بینید که نتایج برای یک قضیه 2000 ساله چندان هم بد نیست.

اگر این مطلب برایتان مفید بوده است آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• قضیه فیثاغورس و کاربردهای شگفت‌ انگیز آن — به زبان ساده
• آموزش ریاضی پایه دانشگاهی
• مجموعه آموزش های رایگان ریاضی و فیزیک
• آموزش ریاضی عمومی ۱ (حل مثال و تست کنکور کارشناسی و ارشد)
• مجموعه آموزش‌های ریاضیات

==