کاربرد جبر خطی در یادگیری عمیق
برای یادگیری بسیاری از مباحث علمی نیاز به آموختن دانشهای پایهای مرتبط با آنها است. هوش مصنوعی و یادگیری ماشین از جمله علومی هستند که این روزها علاقمندان زیادی را در بخشهای صنعت و دانشگاه به خود جذب کردهاند. همچون دیگر حوزههای دانش، یادگیری این دو مبحث نیز نیازمند آموختن پیشنیازهایی است که حتی میتوان گفت جزئی جدا نشدنی از آنها هستند. شاید اولین زمینهای که یادگیری آن به عنوان پیشنیاز و یا همنیاز مبحث هوش مصنوعی به ذهن افراد برسد، زبانهای برنامهنویسی باشد.
اگرچه زبانهای برنامهنویسی (چه محاسباتی و چه اسکریپتنویسی) بخش مهمی از مباحث هوش مصنوعی را تشکیل میدهند و برای پیادهسازی الگوریتمها و مفاهیم این علم مورد استفاده قرار میگیرند، اما یادگیری «ریاضیات و جبرخطی» از اینرو که مبنای ساخت این دانش و دیگر علوم مرتبط با آن بوده بسیار حائز اهمیت و اجتنابناپذیر است. در پس کلیه الگوریتمهای هوش مصنوعی و مفاهیم این حوزه، ریاضیات و جبر خطی نهفته است. بدون داشتن تسلط کافی بر مفاهیم جبر خطی، فرد قطعا در یادگیری هوش مصنوعی دچار اشکال خواهد شد.
از همینرو در بحث یادگیری عمیق، به عنوان یکی از زیرشاخههای هوش مصنوعی مرتبط با بحث شبکههای عصبی مصنوعی، نیاز به آموختن برخی مفاهیم جبر خطی به ویژه مباحث مرتبط با بردارها، ماتریسها و عملیات روی آنها است. جبرخطی، شکل پیوسته ریاضیات گسسته است که اغلب دانشمندان علوم رایانه تجربه کار با آن را دارند. درک عمیق این علم برای آموختن و کار با الگوریتمهای یادگیری ماشین الزامی است.
چرا ریاضیات؟
جبر خطی، احتمالات و حساب دیفرانسیل و انتگرال، زبانهایی هستند که یادگیری ماشین با استفاده از آنها رابطهسازی (فرموله) شده است. یادگیری این مباحث منجر به ایجاد درک عمیقی از ساز و کار الگوریتمهای موجود و ساخت الگوریتمهای جدید میشود.
در پس الگوریتمهای یادگیری عمیق نیز مفاهیم جبر خطی نهفته است و بنابراین پیش از یادگیری و پیادهسازی آنها با زبانهای برنامهنویسی، باید این مفاهیم را آموخت. اسکالرها، بردارها، ماتریسها و تانسورها، ساختارهای پایهای موجود در یادگیری عمیق را تشکیل میدهند. در ادامه هر یک از این مفاهیم توضیح داده میشوند.
کمیت
در لغتنامه دهخدا «کمیت» را چندی و در مقابل کیفیت یا چونی تعریف کردهاند. کمیت در واقع مقدار چیزی است که سنجیده، پیموده یا شمرده شود. به عبارت دیگر، مقدار، اندازه و تعداد چیزی را کمیت آن گویند. کمیت و مقدار دو لفظ مترادف هستند. کمیتها به دو نوع نردهای (اسکالر یا عددی) و برداری تقسیم میشوند.
کمیت نردهای
کمیت نردهای یا اسکالر، با یک عدد نمایش داده میشود. برای مثال، فاصله دو نقطه (پنج متر) یک کمیت نردهای است. کمیتهای نردهای برخلاف کمیتهای برداری فاقد جهت هستند. در واقع کمیت نردهای، یک تانسور مرتبه صفر است. از دیگر کمیتهای نردهای میتوان به جرم، انرژی، دما و چگالی اشاره کرد. عبارت x ∈ ℝ حاکی از آن است که x یک کمیت اسکالر متعلق به مجموعه اعداد حقیقی ℝ است.
مجموعه دادههای گوناگونی در بحث یادگیری عمیق مورد استفاده قرار میگیرند. ℕ یک مجموعه داده از اعداد صحیح مثبت (...،۱،۲،۳) و ℤ مجموعهای از اعداد صحیح مثبت، منفی و صفر است. ℚ مجموعهای از اعداد گویا است که به صورت کسر دو عدد صحیح نشان داده میشود. از جمله اسکالرهای موجود در پایتون میتوان به نوع صحیح (int)، شناور (float)، بایت (byte) و یونیکد (Unicode) اشاره کرد. در کتابخانه NumPy پایتون، ۲۴ نوع داده پایه برای تعریف انواع اسکالرها موجود است.
تعریف اسکالرها و انجام عملیات روی آنها در پایتون
در قطعه کد زیر، برخی از عملیات ریاضی روی کمیتهای اسکالر در پایتون انجام شده است.

با استفاده از قطعه کد زیر میتوان اسکالر بودن یا نبودن یک متغیر را مورد بررسی قرار داد.

کمیت برداری
یک کمیت که توسط چند اسکالر (برای مثال اندازه و جهت) تعریف شود را بردار گویند. بردارها در واقع آرایههای مرتب شدهای از اعداد هستند. یک بردار، نمونهای از تانسور مرتبه اول است. بردارها خود بخشی از چیزی هستند که با عنوان فضای برداری شناخته میشود.
یک فضای برداری را میتوان به عنوان مجموعهای از همه بردارهای محتمل دارای طول مشخص (یا بُعد) در نظر گرفت. یک فضای برداری سهبُعدی مقدارگذاری شده با اعداد حقیقی، به صورت ℝ^3 نشان داده میشود و اغلب به عنوان نمایش جهان واقعی از فضای سهبعدی بهصورت ریاضی بهکار میرود.

برای تبیین مولفههای لازم جهت بیان یک بردار، iاُمین مولفه بردار به صورت [x[i نوشته میشود.
در یادگیری عمیق، معمولا از بردارها برای نمایش بردار ویژگیها که با مولفههای اصلی خود میزان مرتبط بودن یک ویژگی مشخص را نمایش میدهند، مورد استفاده قرار میگیرند. بردار ویژگی میتواند در بر گیرنده اهمیت شدت یک مجموعه از پیکسلها در یک فضای دوبُعدی، تصویر یا تاریخچه مقادیر قیمتها در ابزارهای مالی باشد.
تعریف بردارها و اجرای برخی عملیات روی آنها در پایتون

ماتریسها
ماتریسها آرایههایی مستطیل شکل از اعداد هستند و در واقع تانسورهای مرتبه دوم محسوب میشوند. اگر m و n را اعداد صحیح مثبت در نظر بگیریم، که در آن m, n ∈ ℕ باشند، در نتیجه ماتریس m×n شامل اعداد m*n با m سطر و n ستون است. یک ماتریس m×n کامل را میتوان به صورت زیر نوشت:

خلاصهسازی کل مولفههای ماتریس با شیوه نمایشی که در ادامه نشان داده شده، میتواند مفید باشد:

در زبان برنامهنویسی پایتون، از کتابخانه Numpy استفاده میشود که امکان ساخت آرایههای nبُعدی که اساسا ماتریسها هستند را فراهم میکند. با استفاده از متُد لیست و پاس دادن در لیستها، میتوان یک ماتریس را تعریف کرد.
تعریف ماتریسها و انجام عملیات روی آنها در پایتون
تعریف ماتریسها: در قطعه کد زیر، در خط اول کتابخانه جبر خطی (محاسبات ماتریسی) numpy فراخوانی میشود (و آن را به عنوان np تعریف میکند تا فراخوانی آن در سراسر کد آسانتر باشد). سپس با مقادیر ۱، ۲ و ۲، ۳ یک ماتریس دوبُعدی ایجاد میکند.
np.matrix از یک شی آرایه مانند، یا رشته داده، ماتریکس میسازد. در نهایت، از محور افقی و در ادامه از ردیفها (سطرها) میانگین گرفته است. سپس درخواست اعلام شکل ماتریس (ابعاد) داده شده است.
جمع ماتریسها: ماتریسها را میتوان با کمیتهای اسکالر، بردارها و دیگر ماتریسها جمع کرد. هر یک از این عملیات تعریف مشخصی برای خود دارند. این روشها معمولا در یادگیری ماشین و یادگیری عمیق استفاده میشوند و بنابراین آشنا شدن با آنها بسیار ارزشمند است.
جمع ماتریس با ماتریس: برای جمع دو ماتریس A و B داریم: C = A + B، که در آن باید شکل (ابعاد) هر دو ماتریس A و B یکی باشد. ماتریس حاصل از جمع این دو، دارای شکلی مشابه ماتریسهای A و B است. اگر شکل ماتریسها یکی نباشد، پایتون در خروجی پیغام خطای «addition is not possible» را نمایش میدهد.
جمع ماتریس با کمیت اسکالر: در جمع ماتریس با کمیتهای نردهای، باید عدد را با تک به تک درایههای ماتریس جمع کنیم.
ضرب ماتریس در کمیت اسکالر: برای ضرب ماتریس و کمیت اسکالر، باید عدد موجود را تک به تک در درایههای ماتریس ضرب کنیم.
ضرب ماتریسها: همانطور که در تصویر زیر نشان داده شده، حاصلضرب ماتریس A با ابعاد m x n و B با ابعاد n x p برابر است با ماتریس C با ابعاد m x p.
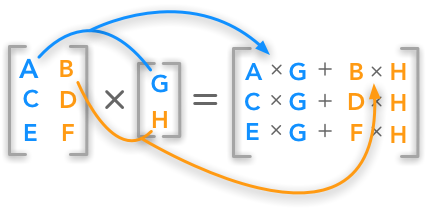
ترانهاده ماتریس: ترانهاده یک ماتریس مانند A، ماتریس دیگری است که با نماد AT نشان داده میشود. برای ایجاد ترانهاده یک ماتریس باید سطرهای آن را به شکل ستون و ستونهای آن را به شکل سطر نوشت. به عبارت دیگر، یک ماتریس m×n تبدیل به ماتریس n×m میشود.
A=[aij]mxn
AT=[aji]n×m
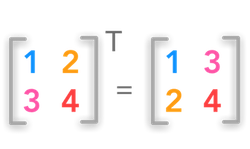
تانسورها
تانسور یک عنصر هندسی است که در ریاضیات جهت توسعه مفاهیم کمیتهای اسکالر، بردارها و ماتریسها مطرح میشود. تانسور در واقع آرایهای از اعداد است که در یک جدول قرار گرفتهاند. تانسور در سادهترین حالت یک عضو دارد که در واقع همان کمیت اسکالر است.
در حالت پیشرفتهتر، تانسور مرتبه اول در واقع آرایهای از اعداد است. تانسورهای دارای دو بعد یا بیشتر، با نام ماتریس شناخته شدهاند. در یادگیری ماشین گاهی نیاز است از تانسورهایی با مرتبه بالاتر از دو استفاده شود. به جای استفاده از ماتریسهای تو در تو، میتوان از کتابخانه Tensorflow یا PyTorch برای اعلان تانسورها استفاده کرد.
برخی اعمال حسابی انجام شده روی تانسورها در زبان پایتون در ادامه آورده شدهاند.
اگر نوشته بالا برای شما مفید بوده است، مطالب زیر نیز به شما پیشنهاد میشود:
- آموزش جبر خطی
- آموزش جبر خطی با متلب
- کاربرد جبر خطی در علم دادهها و یادگیری ماشین - بخش اول
- کاربرد جبر خطی در علم دادهها و یادگیری ماشین - بخش دوم
- آموزش یادگیری عمیق (Deep learning)
^^












