کشیدگی — تعریف و شیوه محاسبه

یکی از مسائل بحث برانگیز در آمار، «کشیدگی» (Kurtosis) است و شاید هنوز عده‌ای در رابطه با مفهوم آن سردرگم باشند. در سال 1905 «کارل پیرسون» (Karl Pearson) دانشمند آمار، برای نشان دادن عدم همخوانی قله یا نوک منحنی برای بعضی از توزیع‌های آماری نسبت به توزیع نرمال، شاخصی را معرفی کرد. او برای توزیع‌هایی که مقدار قله منحنی آن‌ها برجسته‌تر از منحنی نرمال بود، اصطلاح «کشیده» (leptokurtic)  را به کار برد. همچنین وی عبارت «پخی» (platykurtic) را برای توزیع‌هایی معرفی کرد که هموارتر بودند. برای زمانی‌که هیچکدام از حالت‌های قبلی رخ نداده باشد، او منحنی توزیع داده‌ها را «کشیدگی متوسط» (Mesokurtic) نام‌گذاری کرده است.

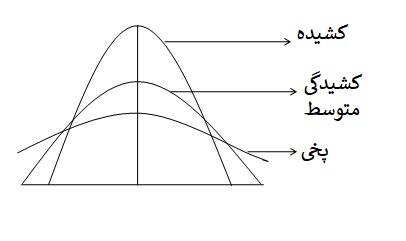
تعریف کشیدگی

در سال 2014 «وست‌فال» (Wesfall) در مقاله‌ای به خصوصیات ضریب کشیدگی پیرسون پرداخت و مفهوم آن را مشخص کرد. ولی متاسفانه هنوز در تفسیر ضریب کشیدگی اشتباهاتی حتی در سطح دانشگاهی وجود دارد.

بعضی به اشتباه ضریب کشیدگی را به عنوان خاصیت قله‌گی (Pickedness) می‌دانند و بعضی نیز به عنوان معیاری برای سنجش خصوصیات بین قله و دم منحنی توزیع در نظر می‌گیرند. ولی وست‌فال تاکید می‌کند که میزان کشیدگی، معیاری برای سنجش میزان جابجایی جرم احتمال از «شانه‌ها» (Shoulders) به سوی مرکز یا دم‌های منحنی توزیع داده‌ها است.

محاسبه کشیدگی

پیرسون برای محاسبه ضریب کشیدگی از گشتاور مرتبه چهار استفاده کرد. اگر $$\mu$$ میانگین و $$\sigma$$ انحراف معیار متغیر تصادفی X باشند، آنگاه ضریب کشیدگی $$Kur(X)$$ به صورت زیر خواهد بود:

$$Kurt(X)=E[(\dfrac{X-\mu}{\sigma})^4]=\dfrac{\mu_4}{\sigma^4}$$

توجه داشته باشید که منظور از E امید-ریاضی متغیر تصادفی است.

فیلم آموزش کنترل کیفیت آماری در فرادرس

کلیک کنید

با توجه به مفهوم چولگی مشخص است که رابطه زیر بین آن و کشیدگی برقرار است. به این معنی که توان دوم ضریب چولگی بعلاوه 1، کران پایین برای ضریب کشیدگی خواهد بود.

$$Kurt(X)=\dfrac{\mu_4}{\sigma^4}\geq (\dfrac{\mu_3}{\sigma^3})^2+1$$

محاسبه کشیدگی نمونه‌ای

از آنجایی که میزان کشیدگی طبق فرمول بالا برای توزیع نرمال برابر با ۳ است، برای سادگی در تفسیر میزان کشیدگی و مقایسه آن با توزیع نرمال، مقدار ۳ واحد از میزان کشیدگی کم می‌کنند و به آن «کشیدگی اصلاح شده» (Exceed Kurtosis) می‌گویند. در بیشتر نرم‌افزارهای آماری، محاسبه میزان کشیدگی براساس این اصلاح انجام می‌پذیرد. به همین دلیل در اکثر موارد، کشیدگی اصلاح شده همان کشیدگی نامیده می‌شود.

برای نمونه‌ای با حجم n مقدار شیوه محاسبه میزان کشیدگی اصلاح شده $$g_2$$ به صورت زیر خواهد بود.

$$g_2=\dfrac{m_4}{m_2^2}-3=\dfrac{\tfrac{1}{n}\sum (x_i-\overline{x})^4}{(\tfrac{1}{n}\sum(x_i-\overline{x})^2)^2}-3$$

اگر x‌ها را به نمره استاندارد تبدیل کنیم، فرم ساده‌تری نیز برای میزان کشیدگی می‌توان نوشت. اگر z‌ نمره استاندارد داده‌ها باشد، میزان کشیدگی به صورت زیر محاسبه می‌شود.

$$g_2=\dfrac{1}{n}\sum z_i^4-3$$

نکته: برای استخراج نمرات استاندارد، هنگام محاسبه انحراف استاندارد باید مجموع مربعات اختلافات از میانگین را به جای  n-1‌ به n‌ تقسیم کرد و از نتیجه جذر گرفت.

برای آشنایی بیشتر با نمره استاندارد و نحوه محاسبه آن می‌توانید به مطلب اندازه‌های پراکندگی --- به زبان ساده مراجعه کنید.

مثال

اگر داده‌های یک نمونه از جامعه به صورت 0, 3, 4, 1, 2, 3, 0, 2, 1, 3, 2, 0, 2, 2, 3, 2, 5, 2, 3, 999 باشند، نمرات استاندارد به صورت زیر محاسبه خواهند شد:

−0.239, −0.225, −0.221, −0.234, −0.230, −0.225, −0.239, −0.230, −0.234, −0.225, −0.230, −0.239, −0.230, −0.230, −0.225, −0.230, −0.216, −0.230, −0.225, 4.359

حال اگر همه این مقدارها را به توان ۴ برسانیم، داده‌های زیر تولید می‌شود:

0.003, 0.003, 0.002, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.003, 0.002, 0.003, 0.003, 360.976

با محاسبه میانگین این داده‌ها و کسر مقدار ۳ از آن، میزان کشیدگی اصلاح شده بدست می‌آید که برابر است با 15.05=3 - 18.05. با توجه به اینکه میزان کشیدگی مثبت شده، منحنی توزیع داده‌ها حالت برجسته‌تر یا کشیده‌تری نسبت به منحنی نرمال دارد.

شکل توزیع احتمال برای این داده‌ها در سمت راست تصویر زیرین دیده می‌شود. همانطور که مشخص است، وجود نقطه انتهایی باعث ایجاد کشیدگی در منحنی توزیع شده است زیرا اکثر داده‌ها در نقطه مرکزی متمرکز شده‌اند و تنها یک داده در انتها دیده می‌شود. ولی در تصویر سمت چپ دیده می‌شود، اگر مقدار انتهایی حذف شود، منحنی نیز کشیدگی نخواهد داشت.

کشیدگی بر اساس همه داده‌ها برابر است با  15.05	کشیدگی داده‌ها با حذف نقطه دورافتاده برابر است با 0.2132-

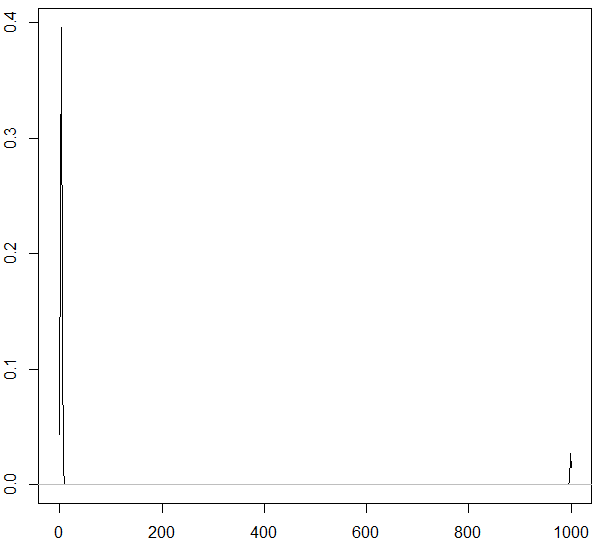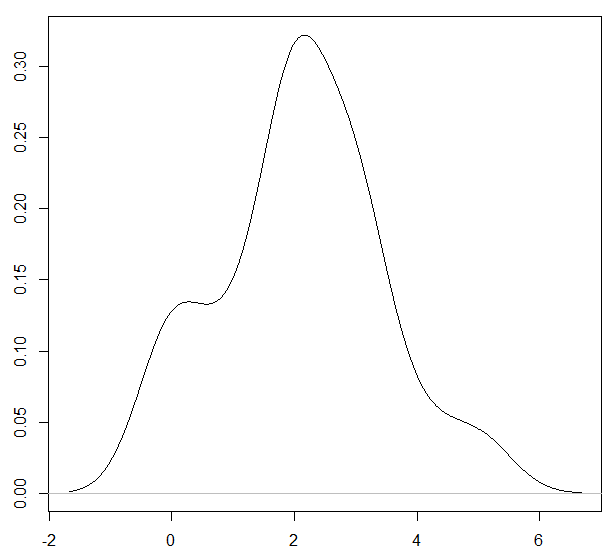از آنجایی که در محاسبه میزان کشیدگی، توان چهار برای تفاضل بین میانگین و مقدارها (گشتاور مرکزی مرتبه چهار) به کار رفته است، مشخص می‌شود که داده‌هایی که بیش از دو یا سه انحراف معیار از میانگین فاصله دارند (مثلا نقاط دورافتاده) نقش بیشتری در محاسبه میزان کشیدگی نسبت به نقاط نزدیک به میانگین (نقاط نزدیک به قله منحنی) دارند.

با وجود داده دورافتاده در مثال قبل، میزان کشیدگی 15.05 است که نشانگر کشیدگی برای منحنی است. همچنین ارتفاع منحنی برابر با 0.4 است. در صورتی که کشیدگی با حذف این نقطه به 0.2132- خواهد رسید و ارتفاع منحنی نیز برابر با 0.32 خواهد بود.

در نتیجه شاخص کشیدگی بیشتر بیانگر میزان دوری داده‌ها از مرکز است تا خاصیت قله‌گی منحنی توزیع احتمال. این حالت در مثال قبل به وضوح دیده می‌شود. با توجه به مقیاس محور عمودی برای هر دو منحنی، مشخص است که ارتفاع منحنی توزیع در حالتی که داده دورافتاده (۹۹۹) وجود داشت بیشتر از حالتی است که آن داده را حذف کردیم.

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های SPSS
• مجموعه آموزش های Minitab
• مفاهیم آماری – شاخص‌های توصیفی
• توزیع فراوانی – به زبان ساده
• مقایسه معیارهای تمرکز (میانگین، میانه، نما)
• مجموعه آموزش‌های نرم‌افزارهای آماری
• اندازه‌های پراکندگی --- به زبان ساده
• چولگی --- تعاریف و شیوه محاسبه

^^