تولید ترکیب ها در جاوا — از صفر تا صد

در این راهنما به بررسی راه‌حل‌های مسئله k-ترکیب در جاوا می‌پردازیم. ابتدا الگوریتم‌های بازگشتی و تکراری را بررسی کرده و پیاده‌سازی می‌کنیم تا همه ترکیب‌های با اندازه مفروض را بسازیم. سپس راه‌حل‌ها را با استفاده از کتابخانه‌های رایج مورد بررسی قرار می‌دهیم. بدین ترتیب قادر خواهیم بود مسائل مربوط به تولید ترکیب را در جاوا حل کنیم.

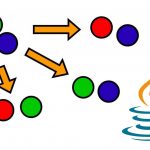
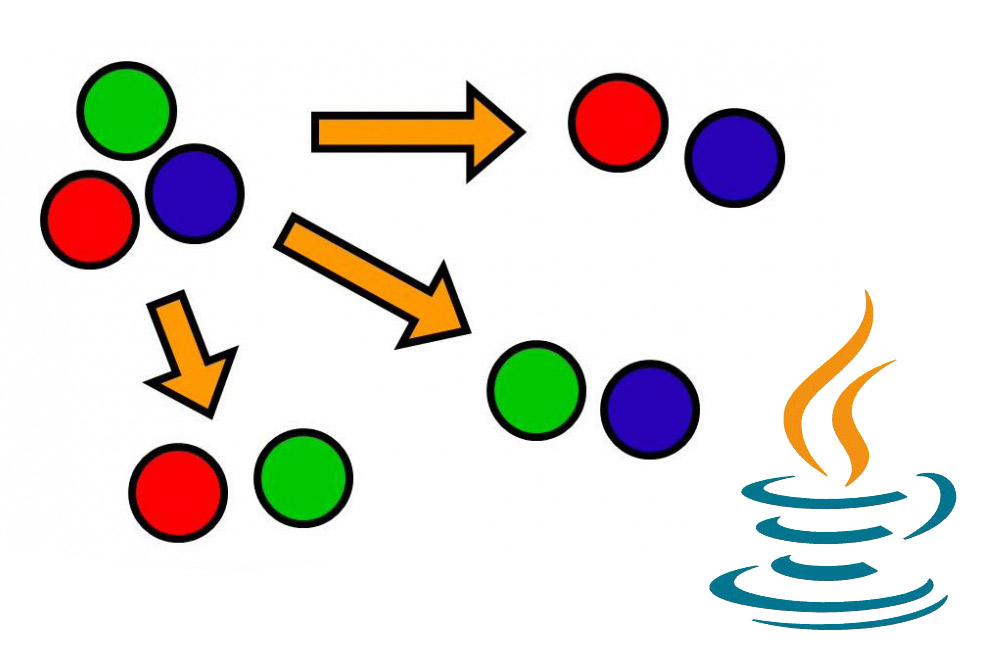
مروری بر ترکیب‌ها

یک ترکیب به بیان ساده به زیرمجموعه‌ای از عناصر موجود در یک مجموعه مفروض گفته می‌شود. در ترکیب برخلاف جایگشت، ترتیب عناصری که در زیر مجموعه انتخاب می‌شوند اهمیتی ندارند. تنها نکته مهم برای ما این است که آیا عنصر معینی در زیرمجموعه انتخابی وجود دارد یا نه.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

برای نمونه در یک بازی کارتی ما باید 5 کارت را از میان دسته‌ای از 52 کارت انتخاب کنیم. هیچ علاقه‌ای به ترتیب انتخاب این 5 کارت نداریم؛ بلکه تنها می‌خواهیم بدانیم کدام کارت‌ها را در دست خود داریم.

برخی مسائل نیازمند ارزیابی همه ترکیب‌های ممکن هستند. به این منظور باید ترکیب‌های مختلف را بشماریم. تعداد روش‌های متمایز انتخاب r عنصر از میان عناصر مجموعه n عضوی را از نظر ریاضیاتی می‌توان با فرمول زیر نمایش داد:

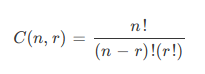
از این رو تعداد روش‌های انتخاب عناصر در سناریوی بدترین حالت به صورت نمایی رشد می‌کند. بدین ترتیب در مورد جمعیت‌های بزرگ، امکان احصای راه‌حل‌های مختلف وجود ندارد.

در چنین مواردی ما می‌توانیم به صورت تصادفی چند گزیده گویا از جامعه را انتخاب کنیم. در ادامه الگوریتم‌های مختلف برای فهرست کردن ترکیب‌ها را بررسی می‌کنیم.

الگوریتم‌های بازگشتی برای تولید ترکیب‌ها

الگوریتم‌های بازگشتی عموماً از طریق افراز یک مسئله به مسائل کوچک‌تر مشابه عمل می‌کنند. این فرایند تا زمانی ادامه می‌یابد که به شرط پایانی برسیم که همان حالت مبنا است. سپس مستقیماً حالت مبنا را حل می‌کنیم.

در ادامه دو روش برای تقسیم وظیفه انتخاب عناصر از یک مجموعه به اجزای کوچک‌تر را مورد بررسی قرار می‌دهیم. رویکرد نخست، تقسیم کردن مسئله برحسب عناصر موجود در مجموعه است. رویکرد دوم مسئله را به وسیله ردگیری صرف عناصر منتخب تقسیم می‌کند.

افراز کردن از طریق عناصر موجود در کل مجموعه

در این بخش وظیفه انتخاب کردن r عنصر از n آیتم را به وسیله بازبینی یک به یک آیتم‌ها انجام می‌دهیم. در مورد هر آیتم در مجموعه می‌توانیم یا آن را در گزینش خود بگنجانیم یا آن را کنار بگذاریم.

ما آیتم اول را در گزینش خود قرار می‌دهیم، سپس باید r-1 عنصر را از میان n-1 آیتم باقیمانده انتخاب کنیم. از سوی دیگر اگر آیتم نخست را کنار بگذاریم، در این صورت باید r عنصر را از میان n-1 آیتم باقی‌مانده انتخاب کنیم.

این وضعیت از نظر ریاضیاتی به صورت زیر توصیف می‌شود:

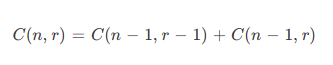
اینک به بررسی پیاده‌سازی بازگشتی این رویکرد می‌پردازیم:

1private void helper(List<int[]> combinations, int data[], int start, int end, int index) {
2    if (index == data.length) {
3        int[] combination = data.clone();
4        combinations.add(combination);
5    } else if (start <= end) {
6        data[index] = start;
7        helper(combinations, data, start + 1, end, index + 1);
8        helper(combinations, data, start + 1, end, index);
9    }
10}

متد کمکی دو فراخوانی بازگشتی به خود ارائه می‌کند. فراخوانی نخست شامل عنصر کنونی است. فراخوانی دوم عنصر کنونی را کنار می‌گذارد.

سپس تولیدکننده ترکیب را با استفاده از متد کمکی می‌نویسیم:

1public List<int[]> generate(int n, int r) {
2    List<int[]> combinations = new ArrayList<>();
3    helper(combinations, new int[r], 0, n-1, 0);
4    return combinations;
5}

در کد فوق متد generate فراخوانی نخست به متد کمکی را تنظیم کرده و پارامترهای مناسب را ارسال می‌کند.

سپس این متد را برای تولید ترکیب‌ها فراخوانی می‌کنیم:

1List<int[]> combinations = generate(N, R);
2for (int[] combination : combinations) {
3    System.out.println(Arrays.toString(combination));
4}
5System.out.printf("generated %d combinations of %d items from %d ", combinations.size(), R, N);

در زمان اجرای برنامه، خروجی زیر را به دست می‌آوریم:

1[0, 1]
2[0, 2]
3[0, 3]
4[0, 4]
5[1, 2]
6[1, 3]
7[1, 4]
8[2, 3]
9[2, 4]
10[3, 4]
11generated 10 combinations of 2 items from 5

در نهایت حالت تست را می‌نویسیم:

1@Test
2public void givenSetAndSelectionSize_whenCalculatedUsingSetRecursiveAlgorithm_thenExpectedCount() {
3    SetRecursiveCombinationGenerator generator = new SetRecursiveCombinationGenerator();
4    List<int[]> selection = generator.generate(N, R);
5    assertEquals(nCr, selection.size());
6}

به سادگی مشاهده می‌شود که اندازه پشته مورد نیاز برابر با تعداد عناصر مجموعه است. زمانی که تعداد عناصر موجود در مجموعه بزرگ و برای نمونه بالاتر از بیشینه عمق پشته فراخوانی باشد، با سرریز پشته مواجه می‌شویم و خطای StackOverflowError را دریافت می‌کنیم. از این رو این رویکرد در صورت بزرگ بودن ورودی عملی نخواهد بود.

افراز کردن به وسیله عناصر موجود در ترکیب

در این روش به جای ردگیری عناصر در مجموعه ورودی، وظیفه مورد نظر را با ردگیری آیتم‌ها در زیرمجموعه انتخابی اجرا می‌کنیم. ابتدا، آیتم‌های موجود در مجموعه ورودی را با استفاده از اندیس‌های 1 تا n مرتب می‌کنیم. سپس می‌توانیم آیتم نخست را از میان n-r+1 آیتم موجود انتخاب کنیم.

فرض کنید که آیتم K-اُم را انتخاب کرده‌ایم. سپس باید r-1 آیتم را از میان n-k آیتم که از k+1 تا n اندیس‌گذاری شده‌اند انتخاب کنیم. این فرایند از نظر ریاضیاتی به صورت زیر توصیف می‌شود:

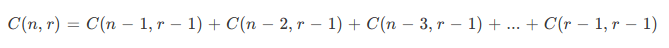
سپس متد بازگشتی را برای پیاده‌سازی این رویکرد می‌نویسیم:

1private void helper(List<int[]> combinations, int data[], int start, int end, int index) {
2    if (index == data.length) {
3        int[] combination = data.clone();
4        combinations.add(combination);
5    } else {
6        int max = Math.min(end, end + 1 - data.length + index);
7        for (int i = start; i <= max; i++) {
8            data[index] = i;
9            helper(combinations, data, i + 1, end, index + 1);
10        }
11    }
12}

در کد فوق، حلقه for آیتم بعدی را انتخاب می‌کند. سپس متد کمکی ()helper را به صورت بازگشتی برای انتخاب از میان آیتم‌های باقی‌مانده فراخوانی می‌کند. زمانی که تعداد مورد نیاز آیتم‌ها انتخاب شدند حلقه را متوقف می‌کنیم.

سپس از متد helper برای تولید زیرمجموعه‌ها استفاده می‌کنیم:

1public List<int[]> generate(int n, int r) {
2    List<int[]> combinations = new ArrayList<>();
3    helper(combinations, new int[r], 0, n - 1, 0);
4    return combinations;
5}

در نهایت حالت تست را می‌نویسیم:

1@Test
2public void givenSetAndSelectionSize_whenCalculatedUsingSelectionRecursiveAlgorithm_thenExpectedCount() {
3    SelectionRecursiveCombinationGenerator generator = new SelectionRecursiveCombinationGenerator();
4    List<int[]> selection = generator.generate(N, R);
5    assertEquals(nCr, selection.size());
6}

اندازه پشته فراخوانی مورد استفاده این رویکرد برابر با تعداد عناصر موجود در زیرمجموعه انتخابی است. از این رو این رویکرد می‌تواند برای ورودی‌های بزرگ نیز استفاده شود. تنها شرط این است که تعداد عناصر انتخابی کمتر از بیشینه عمق پشته فراخوانی باشد. توجه داشته باشید که اگر تعداد عناصری که باید انتخاب شوند نیز بزرگ باشد، این متد کار نخواهد کرد.

الگوریتم تکراری

در رویکرد «تکراری» (Iterative) ما کار خود را با یک ترکیب اولیه آغاز می‌کنیم. سپس به تولید ترکیب‌های بعدی از ترکیب کنونی ادامه می‌دهیم، تا این که همه ترکیب‌ها را تولید کنیم.

فیلم آموزش ساختمان داده ها و الگوریتم ها در جاوا Java در فرادرس

کلیک کنید

اگر ترکیب‌ها را با ترتیب «لغتنامه‌ای» (lexicographic) تولید کنیم، باید کار خود را از کوچک‌ترین ترکیب لغتنامه‌ای آغاز کنیم. برای به دست آوردن ترکیب بعدی از ترکیب کنونی، باید موقعیت عنصری که در انتهای سمت راست ترکیب کنونی قرار دارد و می‌تواند افزایش یابد را بیابیم. سپس موقعیت را افزایش می‌دهیم تا کوچک‌ترین ترکیب لغتنامه‌ای ممکن سمت راست آن موقعیت را تولید کنیم. کد این رویکرد را به صورت زیر می‌نویسیم:

1public List<int[]> generate(int n, int r) {
2    List<int[]> combinations = new ArrayList<>();
3    int[] combination = new int[r];
4 
5    // initialize with lowest lexicographic combination
6    for (int i = 0; i < r; i++) {
7        combination[i] = i;
8    }
9 
10    while (combination[r - 1] < n) {
11        combinations.add(combination.clone());
12 
13         // generate next combination in lexicographic order
14        int t = r - 1;
15        while (t != 0 && combination[t] == n - r + t) {
16            t--;
17        }
18        combination[t]++;
19        for (int i = t + 1; i < r; i++) {
20            combination[i] = combination[i - 1] + 1;
21        }
22    }
23 
24    return combinations;
25}

در ادامه حالت تست را می‌نویسیم:

1@Test
2public void givenSetAndSelectionSize_whenCalculatedUsingIterativeAlgorithm_thenExpectedCount() {
3    IterativeCombinationGenerator generator = new IterativeCombinationGenerator();
4    List<int[]> selection = generator.generate(N, R);
5    assertEquals(nCr, selection.size());
6}

در بخش بعدی از کتابخانه‌های جاوا برای حل این مسئله کمک می‌گیریم.

کتابخانه‌های جاوا برای پیاده‌سازی مسئله ترکیب‌ها

باید تا آنجا که ممکن است از پیاده‌سازی‌های کتابخانه‌های موجود به جای نوشتن کد خود استفاده کنیم. ما کتابخانه‌های زیر را یافته‌ایم که به پیاده‌سازی ترکیب‌ها کمک می‌کنند:

• Apache Commons
• Guava
• CombinatoricsLib

فیلم آموزش برنامه نویسی جاوا Java در فرادرس

کلیک کنید

کتابخانه Apache Commons

کلاس CombinatoricsUtils در کتابخانه Apache Commons تابع‌های کاربردی زیادی در ارتباط با ترکیب‌ها ارائه می‌کند. به طور خاص متد combinationsIterator یک تکرار کننده را بازگشت می‌دهد که ترکیب‌ها را با ترتیب لغتنامه‌ای بازگشت می‌دهد.

ابتدا وابستگی Maven با نام commons-math3 را به پروژه اضافه می‌کنیم:

1<dependency>
2    <groupId>org.apache.commons</groupId>
3    <artifactId>commons-math3</artifactId>
4    <version>3.6.1</version>
5</dependency>

سپس از متد combinationsIterator برای نمایش ترکیب‌ها استفاده می‌کنیم:

1public static void generate(int n, int r) {
2    Iterator<int[]> iterator = CombinatoricsUtils.combinationsIterator(n, r);
3    while (iterator.hasNext()) {
4        final int[] combination = iterator.next();
5        System.out.println(Arrays.toString(combination));
6    }
7}

کتابخانه Google Guava

کلاس Sets در کتابخانه Google Guava متدهای کاربردی برای عملیات مرتبط با مجموعه ارائه می‌کند. متد combinations همه زیرمجموعه‌های با اندازه مفروض را بازگشت می‌دهد.

ابتدا وابستگی Maven با نام Guava library را به پروژه اضافه می‌کنیم:

1<dependency>
2    <groupId>com.google.guava</groupId>
3    <artifactId>guava</artifactId>
4    <version>27.0.1-jre</version>
5</dependency>

سپس از متد combinations برای تولید ترکیب‌ها استفاده می‌کنیم:

1Set<Set<Integer>> combinations = Sets.combinations(ImmutableSet.of(0, 1, 2, 3, 4, 5), 3);

در این کد ما از متد ImmutableSet.of برای ایجاد یک مجموعه از اعداد مفروض استفاده کرده‌ایم.

کتابخانه CombinatoricsLib

CombinatoricsLib یک کتابخانه ساده جاوا برای محاسبه جایگشت‌ها، ترکیب‌ها، زیرمجموعه‌ها، افرازهای صحیح و ضرب دکارتی است. برای استفاده از آن در پروژه باید وابستگی Maven با نام combinatoricslib3 را به پروژه اضافه کنیم:

1<dependency>
2    <groupId>com.github.dpaukov</groupId>
3    <artifactId>combinatoricslib3</artifactId>
4    <version>3.3.0</version>
5</dependency>

سپس از این کتابخانه برای نمایش ترکیب‌ها استفاده می‌کنیم:

1Generator.combination(0, 1, 2, 3, 4, 5)
2  .simple(3)
3  .stream()
4  .forEach(System.out::println);

اجرای این دستور خروجی زیر را تولید می‌کند:

1[0, 1, 2]
2[0, 1, 3]
3[0, 1, 4]
4[0, 1, 5]
5[0, 2, 3]
6[0, 2, 4]
7[0, 2, 5]
8[0, 3, 4]
9[0, 3, 5]
10[0, 4, 5]
11[1, 2, 3]
12[1, 2, 4]
13[1, 2, 5]
14[1, 3, 4]
15[1, 3, 5]
16[1, 4, 5]
17[2, 3, 4]
18[2, 3, 5]
19[2, 4, 5]
20[3, 4, 5]

برای مشاهده مثال‌های بیشتر می‌توانید به این آدرس (+) مراجعه کنید.

سخن پایانی

در این مقاله اقدام به پیاده‌سازی چند الگوریتم برای تولید ترکیب‌ها کردیم. همچنین چند پیاده‌سازی کتابخانه را مورد بررسی قرار دادیم. به طور معمول بهتر است از این کتابخانه‌ها به جای نوشتن کدهای شخصی استفاده کنیم.

فیلم مجموعه آموزش جاوا Java – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش ترکیب، تساوی و اعمال جبری روی توابع در ریاضی پایه
• مجموعه آموزش‌های جاوا (Java)
• جایگشت و ترکیب — به زبان ساده
• یادگیری ترکیب و جایگشت به همراه مثال های عینی — به زبان ساده
• درک ترکیب در ریاضی با استفاده از مفهوم ضرب — به زبان ساده

==