الگوریتم K–نزدیک‌ترین همسایگی به همراه کد پایتون

«k-نزدیک‌ترین همسایگی» (k-Nearest Neighbors) یک روش ناپارامتری است که در داده‌کاوی، یادگیری ماشین و تشخیص الگو مورد استفاده قرار می‌گیرد. بر اساس آمارهای ارائه شده در وب‌سایت kdnuggets الگوریتم k-نزدیک‌ترین همسایگی یکی از ده الگوریتمی است که بیشترین استفاده را در پروژه‌های گوناگون یادگیری ماشین و داده‌کاوی، هم در صنعت و هم در دانشگاه داشته است.

یکی از دلایل اصلی پرکاربرد بودن الگوریتم‌های طبقه‌بندی (Classification) آن است که «تصمیم‌گیری» یکی از چالش‌های اساسی موجود در اغلب پروژه‌های تحلیلی است. برای مثال، تصمیم‌گیری درباره اینکه آیا مشتری X پتانسیل لازم برای مورد هدف قرار داده شدن در کارزارهای دیجیتال یک کسب‌و‌کار را دارد یا خیر و یا اینکه آیا یک مشتری وفادار است یا نه از جمله مسائل تصمیم‌گیری به حساب می‌آیند که در فرآیند تحلیل قصد پاسخ‌دهی به آن‌ها وجود دارد.

نتایج این تحلیل‌ها بسیار تأمل‌برانگیز هستند و به‌طور مستقیم به پیاده‌سازی نقشه راه در یک سازمان یا کسب‌و‌کار کمک می‌کنند. در این نوشتار، به یکی از روش‌های پرکاربرد طبقه‌بندی، یعنی روش k-نزدیک‌ترین همسایگی پرداخته شده و تمرکز آن بر چگونگی کار کردن الگوریتم و تأثیر پارامترهای ورودی بر خروجی و پیش‌بینی است.

سرفصل مطالبی که در این مطلب به آن‌ها پرداخته شده است:

• چه زمانی باید از الگوریتم k-نزدیک‌ترین همسایگی استفاده کرد؟
• الگوریتم k-نزدیک‌ترین همسایگی چگونه کار می‌کند؟
• پارامتر k چگونه انتخاب می‌شود؟
• شبه کد الگوریتم k-نزدیک‌ترین همسایگی
• پیاده‌سازی k-نزدیک‌ترین همسایگی در پایتون
• مقایسه مدل ارائه شده پایتون در این نوشتار با مدل موجود در scikit-learn

چه زمانی باید از الگوریتم k-نزدیک‌ترین همسایگی استفاده کرد؟

الگوریتم k-نزدیک‌ترین همسایگی برای مسائل طبقه‌بندی و رگرسیون قابل استفاده است. اگرچه، در اغلب مواقع از آن برای مسائل طبقه‌بندی استفاده می‌شود.

فیلم آموزش ریاضی برای یادگیری ماشین + پیاده سازی در پایتون در فرادرس

کلیک کنید

برای ارزیابی هر روشی به طور کلی به سه جنبه مهم آن توجه می‌شود:

1. سهولت تفسیر خروجی‌ها
2. زمان محاسبه
3. قدرت پیش‌بینی

در جدول ۱ الگوریتم نزدیک‌ترین همسایگی با الگوریتم‌های «رگرسیون لجستیک»، «CART» و «جنگل‌های تصادفی» (random forests) مقایسه شده است. همان‌گونه که از جدول مشخص است، الگوریتم k-نزدیک‌ترین همسایگی بر اساس جنبه‌های بیان شده در بالا، نسبت به دیگر الگوریتم‌های موجود در جایگاه مناسبی قرار دارد. این الگوریتم اغلب به دلیل سهولت تفسیر نتایج و زمان محاسبه پایین مورد استفاده قرار می‌گیرد.

جدول ۱. مقایسه مدل‌ها

الگوریتم k-نزدیک‌ترین همسایگی چگونه کار می‌کند؟

برای درک بهتر شیوه کار این الگوریتم، عملکرد آن با یک مثال ساده مورد بررسی قرار گرفته است.

در شکل ۱ نحوه توزیع دایره‌های قرمز (RC) و مربع‌های سبز (GS) را مشاهده می‌کنید.

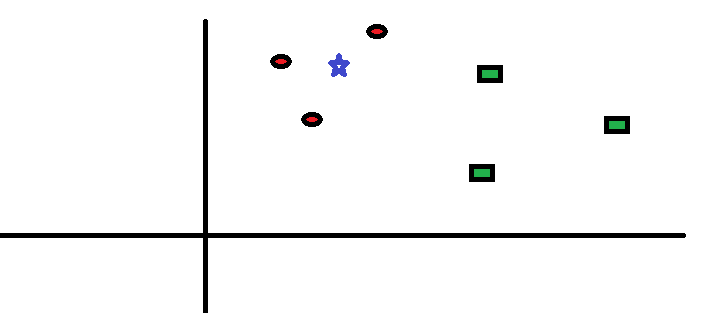
شکل ۱. توزیع نمونه‌ها

فرض کنید قصد پیدا کردن کلاسی که ستاره آبی (BS) متعلق به آن است را دارید (یعنی دایره‌های قرمز). در این مثال در کل دو کلاس دایره‌های قرمز و مربع‌های سبز وجود دارند و ستاره آبی بر اساس منطق کلاسیک می‌تواند تنها متعلق به یکی از این دو کلاس باشد. «K» در الگوریتم k-نزدیک‌ترین همسایگی، تعداد نزدیک‌ترین همسایه‌هایی است که بر اساس آن‌ها رأی‌گیری درباره وضعیت تعلق یک نمونه داده به کلاس‌های موجود انجام می‌شود. فرض کنید k = ۳ است. یک دایره آبی دور سه تا از نزدیک‌ترین همسایه‌های ستاره آبی ترسیم شده (شکل ۲) است. برای جزئيات بیشتر نمودار شکل ۲ را نگاه کنید.

شکل ۲. تعیین کلاس نمونه جدید

سه نقطه نزدیک‌تر به BS، همه دایره‌های قرمز هستند. با میزان اطمینان خوبی می‌توان گفت که ستاره آبی به کلاس دایره‌های قرمز تعلق دارد. در این مثال، انتخاب بسیار آسان است چون هر سه نزدیک‌ترین همسایه ستاره آبی، دایره‌های قرمز هستند و در واقع هر سه رأی متعلق به دایره‌های قرمز است. انتخاب پارامتر k در الگوریتم k-نزدیک‌ترین همسایگی، بسیار حائز اهمیت است. در ادامه عوامل تأثیرگذار بر انتخاب بهترین k، مورد بررسی قرار می‌گیرند.

پارامتر k چگونه انتخاب می‌شود؟

در ابتدا بهتر است تأثیر انتخاب k در الگوریتم k-نزدیک‌ترین همسایگی بر نتایج خروجی مورد بررسی قرار بگیرد. اگر به مثال پیشین توجه کنید، می‌بینید که هر شش نمونه (دایره‌های قرمز و مستطیل‌های سبز) ثابت هستند و تنها انتخاب k می‌تواند مرزهای یک کلاس را دستخوش تغییر کند.

فیلم آموزش تقلیل ابعاد در یادگیری ماشین (رایگان) در فرادرس

کلیک کنید

در ادامه مرزهای دو کلاس که با انتخاب k‌های گوناگون تغییر پیدا می‌کنند (شکل ۳) را مشاهده می‌کنید.

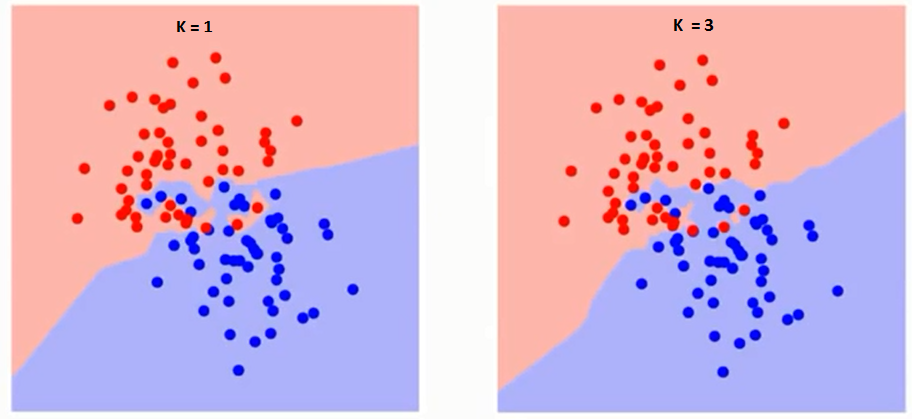
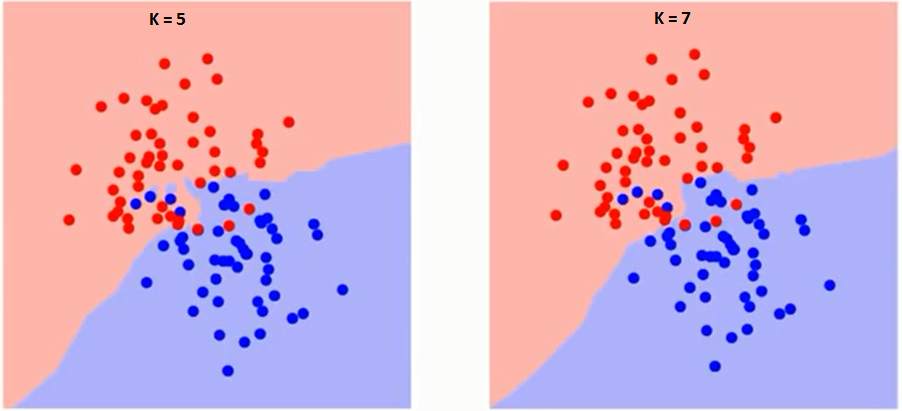
شکل 3. تغییر مرزهای کلاس‌ها با انتخاب k

همان‌طور که از تصاویر مشهود است، با افزایش مقدار k، مرزهای کلاس‌ها روان‌تر می‌شود. با افزایش k به سمت بی‌نهایت، بسته به اکثریت مطلق نمونه‌ها در نهایت یک کلاس آبی یا قرمز وجود خواهد داشت. نرخ خطاهای آموزش (training) و ارزیابی (evaluation) دو عاملی هستند که برای تعیین مقدار k مناسب به آن‌ها نیاز داریم. نمودار خطی در شکل ۴ بر اساس مقدار خطای آموزش برای k‌های گوناگون ترسیم شده است.

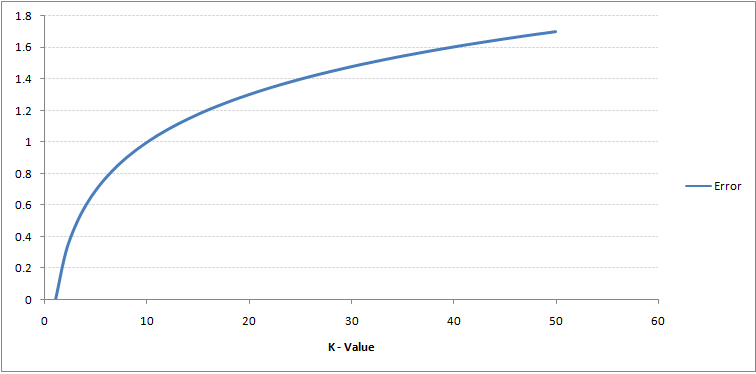
شکل 4. نرخ خطای آموزش برای k‌های گوناگون

چنان‌که مشاهده می‌کنید، نرخ خطا هنگامی‌که k = ۱ است، برای نمونه‌های آموزش صفر باقی می‌ماند. این امر بدین دلیل است که نزدیک‌ترین نقطه به هر داده آموزش، خود آن داده است. بنابراین نتایج پیش‌بینی با k = ۱ صحیح است. اگر k = ۱ باشد نمودار خطای ارزیابی نیز روند مشابهی دارد. نمودار خطای ارزیابی با مقادیر گوناگون k در شکل ۵ نمایش داده شده است.

شکل 5. نرخ خطای ارزیابی برای k‌های گوناگون

هنگامی که k = ۱ است مرزها دچار بیش برازش (overfit) شده‌اند. بنابراین نرخ خطا کاهش پیدا کرده و در واقع به حداقل میزان خود می‌رسد و با افزایش k مقدار خطا نیز افزایش پیدا می‌کند. برای انتخاب مقدار بهینه k می‌توان داده‌های آموزش و ارزیابی را از مجموعه داده اولیه جدا کرد. سپس با رسم نمودار مربوط به خطای ارزیابی مقدار بهینه K را انتخاب کرد. این مقدار از k باید برای همه پیش‌بینی‌ها مورد استفاده قرار بگیرد و در‌ واقع برای همه مراحل پیش‌بینی باید از یک k مشخص استفاده شود.

شبه کد k-نزدیک‌ترین همسایگی

پیاده‌سازی مدل k-نزدیک‌ترین همسایگی با استفاده از شبه کد زیر امکان‌پذیر است:

1. بارگذاری داده‌ها
2. انتخاب اولیه مقدار k
3. برای ایجاد کلاس‌های پیش‌بینی، از مقدار ۱ تا تعداد کل نقاط داده آموزش تکرار شود:
   1. فاصله داده‌های تست از هر سطر مجموعه داده آموزش محاسبه شود. در اینجا از فاصله اقلیدسی به عنوان فاصله سنجش استفاده می‌شود که مرسوم‌ترین روش است. دیگر سنجه‌های قابل استفاده عبارت‌اند از فاصله چبیشف، کسینوس و دیگر موارد
   2. فاصله‌های محاسبه شده بر اساس مقدار فاصله به‌صورت صعودی مرتب شود
   3. سطرهای k بالایی از آرایه مرتب شده انتخاب شود
   4. کلاس‌های دارای بیشترین تکرار در این سطرها دریافت شود
   5. مقدار کلاس پیش‌بینی‌شده بازگردانده شود

پیاده‌سازی الگوریتم K-نزدیک‌ترین همسایگی در پایتون

در ادامه از مجموعه داده معروف Iris برای ساخت مدل KNN استفاده شده است.

فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین در فرادرس

کلیک کنید

این مجموعه داده را می‌توانید از اینجا دانلود کنید.

# Importing libraries
import pandas as pd
import numpy as np
import math
import operator

#### Start of STEP 1
# Importing data
data = pd.read_csv("iris.csv")
#### End of STEP 1
data.head()

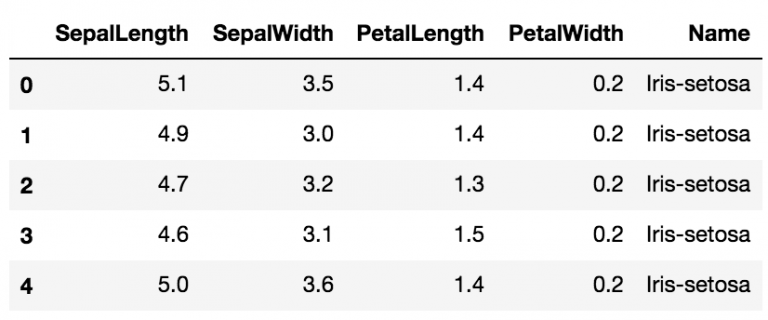
# Defining a function which calculates euclidean distance between two data points
def euclideanDistance(data1, data2, length):
distance = 0
for x in range(length):
distance += np.square(data1[x] - data2[x])
return np.sqrt(distance)
# Defining our KNN model
def knn(trainingSet, testInstance, k):
distances = {}
sort = {}
length = testInstance.shape[1]
#### Start of STEP 3
# Calculating euclidean distance between each row of training data and test data
for x in range(len(trainingSet)):
#### Start of STEP 3.1
dist = euclideanDistance(testInstance, trainingSet.iloc[x], length)
distances[x] = dist[0]
#### End of STEP 3.1
#### Start of STEP 3.2
# Sorting them on the basis of distance
sorted_d = sorted(distances.items(), key=operator.itemgetter(1))
#### End of STEP 3.2
neighbors = []
#### Start of STEP 3.3
# Extracting top k neighbors
for x in range(k):
neighbors.append(sorted_d[x][0])
#### End of STEP 3.3
classVotes = {}
#### Start of STEP 3.4
# Calculating the most freq class in the neighbors
for x in range(len(neighbors)):
response = trainingSet.iloc[neighbors[x]][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
#### End of STEP 3.4
#### Start of STEP 3.5
sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)
return(sortedVotes[0][0], neighbors)
#### End of STEP 3.5

# Creating a dummy testset
testSet = [[7.2, 3.6, 5.1, 2.5]]
test = pd.DataFrame(testSet)

#### Start of STEP 2
# Setting number of neighbors = 1
k = 1
#### End of STEP 2
# Running KNN model
result,neigh = knn(data, test, k)
# Predicted class
print(result)
-> Iris-virginica

# Nearest neighbor
print(neigh)
-> [141]

اکنون با جایگزینی مقدار K، می‌توان شاهد تغییرات نتایج پیش‌بینی‌ها بود:

# Setting number of neighbors = 3
k = 3
# Running KNN model
result,neigh = knn(data, test, k)
# Predicted class
print(result) -> Iris-virginica

# 3 nearest neighbors
print(neigh)
-> [141, 139, 120]

# Setting number of neighbors = 5
k = 5
# Running KNN model
result,neigh = knn(data, test, k)
# Predicted class
print(result) -> Iris-virginica

# 5 nearest neighbors
print(neigh)
-> [141, 139, 120, 145, 144]

مقایسه مدل ارائه شده در این نوشتار با scikit-learn

با استفاده از scikit-learn مطابق قطعه کد زیر، طبقه‌بندی با الگوریتم k-نزدیک‌ترین همسایگی روی داده‌های Iris انجام می‌شود.

from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(data.iloc[:,0:4], data['Name'])
# Predicted class
print(neigh.predict(test))
-> ['Iris-virginica']
# 3 nearest neighbors
print(neigh.kneighbors(test)[1])
-> [[141 139 120]]

هر دو مدل، کلاس مشابه (Iris-virginica) و همسایگی‌های مشابهی ([141 139 120]) را پیش‌بینی کرده‌اند. بنابراین نتیجه گرفته می‌شود که مدل ارائه شده در این نوشتار به شکلی که از آن انتظار می‌رود کار می‌کند.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

سخن پایانی

الگوریتم k-نزدیک‌ترین همسایگی یکی از ساده‌ترین الگوریتم‌های طبقه‌بندی است. اما با وجود سادگی، نتایج آن به وضوح قابل رقابت با دیگر الگوریتم‌ها است. این الگوریتم برای حل مسائل رگرسیون نیز قابل استفاده است. در این راستا، تنها تفاوت آن با روشی که در این نوشتار ارائه شده، استفاده از میانگین نزدیک‌ترین همسایه‌ها به جای رأی‌گیری از نزدیک‌ترین همسایه‌ها است.

• ۳۰ پرسش و پاسخ درباره‌ی الگوریتم نزدیکترین K همسایه
• آموزش‌های مدل سازی، برازش و تخمین
• گنجینه آموزش های برنامه نویسی پایتون (Python)
• آموزش خوشه بندی با استفاده از الگوریتم های تکاملی و فراابتکاری
• آموزش ​اصول و روش های داده کاوی (Data Mining)
• مجموعه آموزش های داده کاوی یا Data Mining در متلب

==

^^