بزرگترین کران پایین (Inf) و کوچکترین کران بالا (Sup) مجموعه — به زبان ساده

یکی از مفهوم‌های کاربردی و مهم در ریاضیات و بخصوص آنالیز ریاضی، اصطلاح بزرگترین کران پایین (Inf) و کوچکترین کران بالا (Sup) است که برای یک مجموعه یا حتی تابع مورد محاسبه قرار می‌گیرد. در دیگر نوشتارهای فرادرس که مرتبط با نظریه اعداد هستند، با مفهوم یا اصل خوش ترتیبی (Well-ordering theorem) آشنا شدید و دیدید که مثلا برای مجموعه اعداد صحیح، خاصیت ترتیب وجود داشته و در اصل خوش‌ترتیبی صدق می‌کند. با استفاده از این اصل و قضیه‌های دیگر وجود بزرگترین کران پایین یا کوچکترین کران بالا برای مجموعه‌ها اثبات می‌شود.

برای آشنایی بیشتر با اصطلاحاتی که در این نوشتار به کار رفته است، بهتر است متن مجموعه ها در ریاضیات – مفاهیم پایه و اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده را مطالعه کنید. همچنین خواندن اکسترمم مطلق — به زبان ساده و ماکزیمم و مینیمم تابع — به زبان ساده نیز خالی از لطف نیست.

بزرگترین کران پایین (Inf) و کوچکترین کران بالا (Sup) مجموعه ها

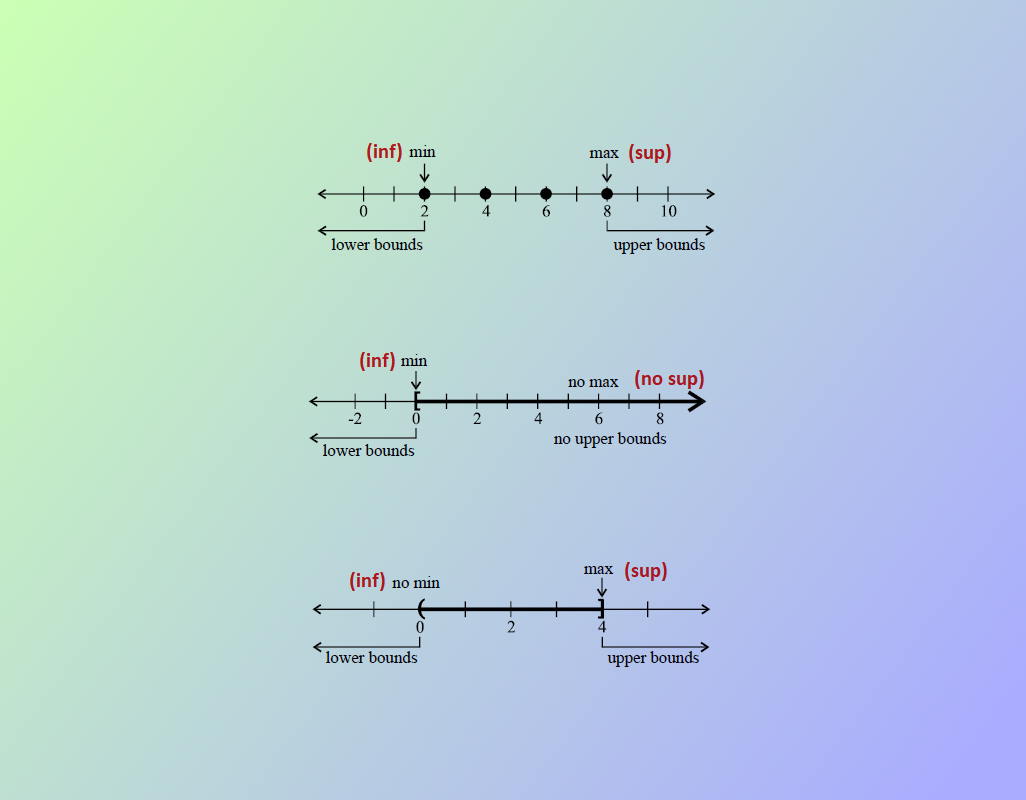
در ریاضیات بزرگترین کران پایین یک مجموعه را با Infimum یا به اختصار Inf نشان می‌دهند. منظور از بزرگترین کران پایین یک مجموعه، بزرگترین مقداری است که از همه عناصر مجموعه کوچکتر است. این امر به مانند مقدار کمینه یا Minimum در یک مجموعه است با این تفاوت که مقدار کمینه یک مجموعه باید عضوی از آن مجموعه باشد ولی در مورد Inf چنین شرطی وجود ندارد.

فیلم آموزش ریاضیات گسسته در فرادرس

کلیک کنید

بنابراین چون Inf ممکن است عضوی از مجموعه مورد نظر نباشد، آن را به عنوان یک کران در نظر می‌گیرند و بزرگترین کران پایین نام‌گذاری کرده‌اند.

از طرفی منظور از کوچکترین کران بالا یک مجموعه که با Supremum یا به اختصار Sup نشان داده می‌شود، کوچکترین مقداری است که از همه اعضای مجموعه بزرگتر است. Sup درست مانند مقدار بیشنیه یا Maximum است، با این تفاوت که مقدار بیشینه باید عضوی از مجموعه باشد ولی در مورد Sup چنین شرطی وجود ندارد.

به همین ترتیب چون Sup ممکن است عضوی از مجموعه اصلی نباشد، آن را به عنوان کران بالا برای مجموعه در نظر می‌گیرند که از بقیه کران‌های بالا، کوچکتر است.

نکته: گاهی Inf را بنا به تعریف به صورت GLB یا بزرگترین کران پایین (Greatest Lower Bound) نیز نشان می‌دهند. همچنین Sup را با نماد LUB یا کوچکترین کران بالا (Least Upper Bound) هم به کار می‌برند.

بزرگترین کران پایین (Inf)

مجموعه‌ $$S$$ که دارای ترتیب جزئی (Partially Ordered Set)  روی مجموعه $$T$$ است را در نظر بگیرید. کران پایین مجموعه $$S$$ به صورت زیر نشان داده می‌شود.

$$\large LB(S)=\{a\in T;\; a\leq x \forall x \in S\}$$

به این ترتیب مقادیری مثل $$a$$، کران پایین مجموعه $$S$$ را تشکیل می‌دهند. واضح است که $$a$$ در مجموعه $$T$$ قرار دارد.

نکته: مجموعه $$T$$ را یک مجموعه مرتب جزئی می‌نامند اگر روی اعضای آن رابطه ترتیبی $$\leq$$ برقرار باشد. چنین وضعیتی را به صورت $$(T,\leq)$$ نشان می‌دهند.

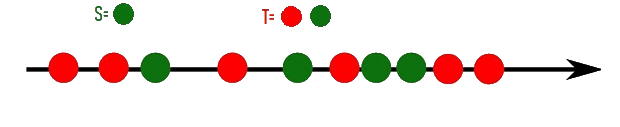
در تصویر بالا، $$T$$ یک مجموعه مرتب جزئی است زیرا توانسته‌ایم اعضای آن را روی محور اعداد به ترتیب نمایش دهیم. از طرفی مجموعه $$S$$ نیز زیر مجموعه‌ای از مجموعه $$T$$ است. حال به دنبال کران‌هایی پایین مجموعه $$S$$ می‌گردیم. واضح است که بزرگترین کران پایین برای $$S$$، همان Inf خواهد بود.

بزرگترین کران پایین یا Inf مجموعه $$S$$ را هم به صورت زیر تعریف می‌کنند.

$$\large a \text{ is inf};\;\; \forall y \in LB(S)\subseteq T, y\leq a$$

این امر به این معنی است که در بین همه کران‌های پایین مجموعه $$S$$، مقدار $$a$$ از همه بزرگتر است. در این صورت می‌نویسیم:

$$\large \inf(S)=a$$

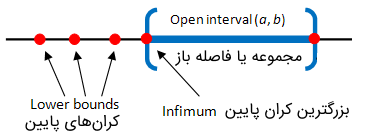
همانطور که در مجموعه‌های باز و بسته توضیح دادیم، فاصله‌های باز مثل $$(a,b)$$ یک مجموعه باز (Open Set) هستند. در این حالت مقدار $$a$$ بزرگترین کران پایین مجموعه باز $$(a,b)$$ است.

نکته: همانطور که خواندید، Inf و Sup ممکن است عضوی از اعضای مجموعه نباشند، در حالیکه Min و Max از اعضای مجموعه مورد نظر هستند.

مثال ۱

بازه $$(1,5)$$ را در نظر بگیرید. از آنجایی که این مجموعه، یک فاصله باز است، مقدار ۱ را بزرگترین کران پایین یا inf این مجموعه می‌نامیم. بنابراین اگر $$A=(1,5)$$ آنگاه $$\inf(A)=1$$.

مثال ۲

دنباله زیر را در نظر بگیرید. مشخص است که صفر، بزرگترین کران پایین این مجموعه محسوب می‌شود.

$$\large S=\{\frac{1}{n}, n \in N\}, \;\;\; \inf(S)=0$$

عناصر این دنباله به صورت زیر هستند:

$$\large S=\{1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\ldots\}$$

واضح است که کوچکترین عضو برای چنین مجموعه‌ای وجود ندارد ولی ۰ عضوی از مجموعه اعداد حقیقی است که از همه اعضای مجموعه $$S$$ کوچکتر بوده ولی از بقیه کران‌های پایین این مجموعه، بزرگتر است. به این ترتیب می‌توان گفت که این دنباله به صفر همگرا است.

نکته: همانطور که مشاهده می‌کنید برای دنباله یا سری‌ها نزولی، وجود بزرگترین کران پایین، می‌تواند برای نشان دادن همگرایی آن‌ها موثر باشد.

کوچکترین کران بالا (Sup)

تعریف کوچکترین کران بالا (Sup) نیز درست به مانند Inf صورت می‌گیرد. مجموعه مرتب جزئی ($$T,\leq$$) را در نظر بگیرید. برای زیر مجموعه $$S$$ از آن، کران پایین به صورت زیر تعریف می‌شود.

$$\large GB(S)=\{b\in T;\; x\leq b \forall x \in S\}$$

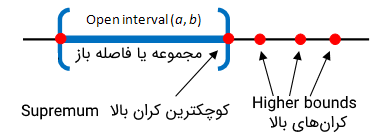
بر همین اساس و به کمک مجموعه $$GB$$، کوچکترین کران بالا را به عنوان Sup‌ مجموعه $$S$$ در نظر می‌گیریم. به عبارت دیگر کوچکترین عضو مجموعه $$GB$$ همان Sup مجموعه $$S$$ خواهد بود.

$$\large b \text{ is sup};\;\; \forall z \in GB(S)\subseteq T, b \leq z$$

مثال ۳

فاصله باز $$(a,b)$$ را در نظر بگیرید. مشخص است که $$b$$ در این مجموعه قرار ندارد ولی یکی از کران‌های بالای مجموعه یا فاصله باز $$(a,b)$$ است. از آنجایی که $$b$$ از همه کران‌های بالای این مجموعه، کوچکتر است، $$b$$ را Sup این مجموعه می‌شناسیم.

$$\large B=(a,b),\;\;b =\sup(B)$$

به این ترتیب کوچکترین کران بالا برای فاصله $$(1,5)$$ برابر است با ۵ زیرا:

$$\large 5 \in GB, \;\; 5 \leq z ,\forall z \in GB$$

مثال ۴

دنباله یا سری زیر را در نظر بگیرید.

$$\large S=\left\{(-1)^{i}-{\tfrac {1}{i}}\mid i=1,2,3,\ldots \right\}$$

اعضای این دنباله به صورت زیر هستند.

$$\large S=\{-2,\frac{1}{2},\frac{-4}{3},\frac{3}{4},\ldots\}$$

همانطور که دیده می‌شود، همه مقادیر مثبت این دنباله، از یک کوچکتر هستند، پس کوچکترین کران بالا برای چنین مجموعه‌ای همان ۱ خواهد بود.

$$\large {\displaystyle \sup \left\{(-1)^{i}-{\tfrac {1}{i}}\mid i=1,2,3,\ldots \right\}=1}$$

خصوصیات Inf و Sup

ممکن است برای یک مجموعه، Inf یا Sup وجود نداشته باشد. مجموعه‌ای که کراندار نباشد، نمی‌تواند بزرگترین کران پایین یا کوچکترین کران بالا داشته باشد. به همین دلیل پیدا کردن Inf یا Sup برایش امری محال خواهد بود.

فیلم آموزش ساختمان گسسته با رویکرد حل مساله در فرادرس

کلیک کنید

قوانین و خصوصیات زیر برای Inf و Sup، همچنین کران‌های بالا و پایین مجموعه، وجود دارد.

• مقدار کمینه (Minimum) در صورت وجود، یکتا است.
• مقدار بیشینه (Maximum) در صورت وجود، یکتا است.
• اگر مقدار کمینه برای مجموعه $$S$$ وجود داشته باشد، Inf آن هم موجود بوده و با هم برابر هستند. $$\min(S)=\inf(S)$$
• گر مقدار بیشینه برای مجموعه $$S$$ وجود داشته باشد، Sup آن هم موجود بوده و با هم برابر هستند. $$\max(S)=\sup(S)$$
• هر مجموعه از بالا کراندار مثل $$S$$ که زیر مجموعه اعداد حقیقی ($$\mathcal{R}$$) باشد،‌ دارای یک Sup است. این امر نشان می‌دهد که مجموعه اعداد حقیقی، کامل (Complete) هستند.

فرض کنید $$A$$ و $$B$$ دو زیر مجموعه از اعداد حقیقی باشند. همچنین در نظر بگیرید که Inf و Sup این دو مجموعه نیز موجود است.

مجموعه‌های $$A+B$$ و $$\lambda A$$ و $$AB$$ را به صورت زیر تعریف می‌کنیم.

$$\begin{align}\large \lambda A& =\large \{ \lambda x : x \in A \},\\ \large A + B &\large = \{ x + y : x \in A, y \in B \}\\ \large AB &\large = \{ xy : x \in A, y \in B \}\end{align}$$

آنگاه خصوصیات زیر برای Inf و Sup در چنین مجموعه‌هایی وجود دارد:

• $$p=\inf(A)$$ اگر و تنها اگر برای هر $$\epsilon>0$$، عضوی از مجموعه $$A$$ مثال $$x$$ وجود داشته باشد که $$x<p+\epsilon$$ و برای هر $$x$$ در $$A$$ داشته باشیم $$x\geq p$$.
• $$p=\sup(A)$$‌ اگر و تنها اگر هر $$\epsilon>0$$، عضوی از مجموعه $$A$$ مثال $$x$$ وجود داشته باشد که $$x>p-\epsilon$$ و برای هر $$x$$ در $$A$$ داشته باشیم $$x\leq p$$.
• اگر $$A$$ زیر مجموعه $$B$$ باشد آنگاه رابطه‌های زیر برای Inf و Sup آن‌ها برقرار است.

$$\large A \subseteq B \rightarrow\; \inf(A) \geq \inf(B),\;\;\;\; \sup(A) \leq \sup(B)$$

• برای هر $$\lambda\geq 0$$ داریم:

$$\large \inf(\lambda A)=\lambda \inf(A) ,\;\; \sup(\lambda A)=\lambda \sup(A) $$

• برای هر $$\lambda< 0$$ خواهیم داشت:

$$\large \inf(\lambda A)=\lambda \sup(A) ,\;\;\;\sup(\lambda A)=\lambda \inf(A) $$

• بین Inf و Sup برای دو مجموعه $$A$$ و $$B$$ و مجموع این دو مجموعه رابطه زیر برقرار است:

$$\large \inf(A+B)=\inf(A)+\inf(B), \;\;\;\sup(A+B)=\sup(A)+\sup(B)$$

• اگر $$A$$ و $$B$$ دو مجموعه ناتهی و با مقادیر نامنفی باشند، آنگاه برای ضرب این مجموعه داریم:

$$\large \inf(AB)=\inf(A)\cdot\inf(B),\;\;\;\sup(AB)=\sup(A)\cdot\sup(B)$$

اگر نگاهمان را به جای اعداد حقیقی به «مجموعه اعداد حقیقی توسعه یافته» (Extended Real Numbers Set) متمرکز کنیم، خصوصیات جالب دیگری برای Inf و Sup پیدا خواهیم کرد. فرض بر این است که برای مجموعه‌ای که از پایین کردان‌دار نیست مثل $$S$$ مقدار Inf به صورت زیر مشخص می‌شود.

$$\large \inf(S)=-\infty$$

و اگر $$S$$ از بالا کراندار نباشد، مقدار Sup را به شکل زیر در نظر می‌گیریم.

$$\large \sup(S)=\infty$$

از آنجایی که در مجموعه تهی ($$\emptyset$$) هیچ عضوی وجود ندارد، همه مقادیر اعداد حقیقی، هم کران بالا و هم کران پایین برای آن محسوب می‌شوند. در نتیجه مقدار Inf و Sup برای مجموعه تهی برابر است با:

$$\large \sup (\emptyset) =\min(\{-\infty ,+\infty \}\cup \mathbb {R} )=-\infty$$

و

$$\large \inf(\emptyset) =\max(\{-\infty ,+\infty \}\cup \mathbb {R} )=+\infty$$

نکته: مجموعه $$\{-\infty,\infty\}\cup R$$ را مجموعه اعداد حقیقی توسعه یافته می‌نامند که شامل دو عضو «مثبت بی‌نهایت» ($$+\infty$$) و «منفی بی‌نهایت» ($$-\infty$$) است.

خلاصه و جمع‌بندی

در این نوشتار به دو مفهوم مرتبط با مجموعه و دنباله‌ها پرداختیم که با عنوان بزرگترین کران پایین (Inf) و کوچکترین کران بالا (Sup) شناخته شده‌اند. یکتایی Inf و Sup برای یک مجموعه یا دنباله، روشی برای نشان دادن همگرایی دنباله‌ها است.

با استفاده از خصوصیاتی که برای Inf و Sup برشمردیم، همگرایی دنباله‌های ریاضیاتی مشخص شده و اثبات می‌شوند. موضوع همگرایی مجموعه‌ها و دنباله‌ها در نوشتار دیگر مورد بحث و بررسی قرار گرفته است ولی در مطالب بعدی به صورت تخصصی و با تکیه بر آنالیز ریاضی به بررسی موضوع همگرایی و اصطلاحات lim sup و lim inf خواهیم پرداخت.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• آموزش مبانی آنالیز حقیقی
• مجموعه آموزش‌ های دروس دانشگاهی
• تقسیم عدد صحیح — به زبان ساده
• مجموعه باز و بسته در ریاضیات --- به زبان ساده
• قواعد بخش پذیری یا عاد کردن — به زبان ساده