فرادرسکره هیل (Hill Sphere) — به زبان ساده
در مطالب گذشته وبلاگ فرادرس در مورد مفاهیم مربوط به گرانش و هم‌چنین دیدگاه سنتی و مدرن نسبت به آن بحث شد. لذا در این مطلب قصد داریم تا در مورد فضایی صحبت کنیم که وابسته به میدان گرانشی بوده و با توجه به اندازه این نیرو تعریف می‌شود. این مفهوم تحت عنوان کره هیل یا شعاع هیل شناخته می‌شود.
کره هیل
به فضای اطراف هر جسم فضایی (ستاره، سیاره و ...) که در آن دیگر اجسام فضایی مشخصا تحت نیروی جاذبه آن هستند، کره هیل گفته می‌شود. برای نمونه به‌منظور این‌که ماه در مدار زمین قرار بگیرد، باید در شعاعی مساوی یا کمتر از کره هیل نسبت به زمین قرار داشته باشد. حتی ماه نیز کره هیل اطراف خودش را دارد. مجموعه زمین و ماه نیز در کره هیل خورشید قرار می‌گیرند. می‌توان گفت هر جسم فضایی که در کره هیل جسم بزرگتری قرار گرفته باشد، ماهواره آن جسم محسوب می‌شود.
این مفهوم توسط ستاره‌شناس آمریکایی، «جورج ویلیام هیل» (George William Hill) تعریف شد. او این تعریف را به کمک مطالعات «ادوارد رُش» (Édouard Roche)، ستاره‌شناس فرانسوی انجام داد. به همین دلیل برخی از منابع این فضا را کره رش نیز می‌نامند. در تصویر زیر کره هیل مربوط به خورشید و زمین نشان داده شده است.
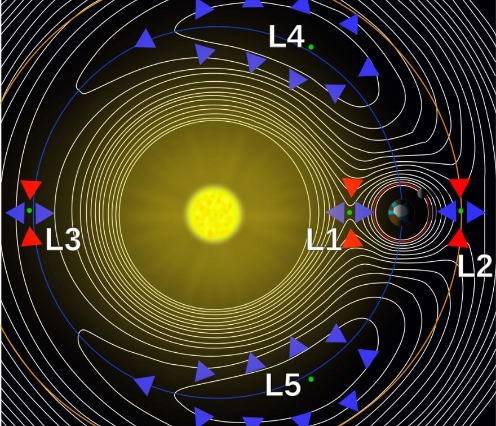
در تصویر فوق ۵ نقطه لاگرانژی بین زمین و خورشید نشان داده شده‌اند. نقاط لاگرانژی، نقاطی هستند که در آن‌ها گرانش دو جسم برابر بوده و در نتیجه یکدیگر را خنثی می‌کنند. همان‌طور که مشاهده می‌کنید به دلیل گرانش قدرتمندتر خورشید، نقطه لاگرانژی بین زمین و خورشید به زمین نزدیک‌تر است. مینیمم قطر شعاع هیل در نقطه‌ای قرار دارد که متصل‌کننده مراکز زمین و خورشید است. از این رو حد شعاع هیل متناسب با این نقاط محاسبه می‌شود. اگر ماه در بیرون از کره هیلِ زمین قرار داشته باشد به دور آن می‌چرخد ولی با گذشت زمان مدار ماه به جای زمین، به دور خورشید ثابت خواهد شد.
روابط حاکم
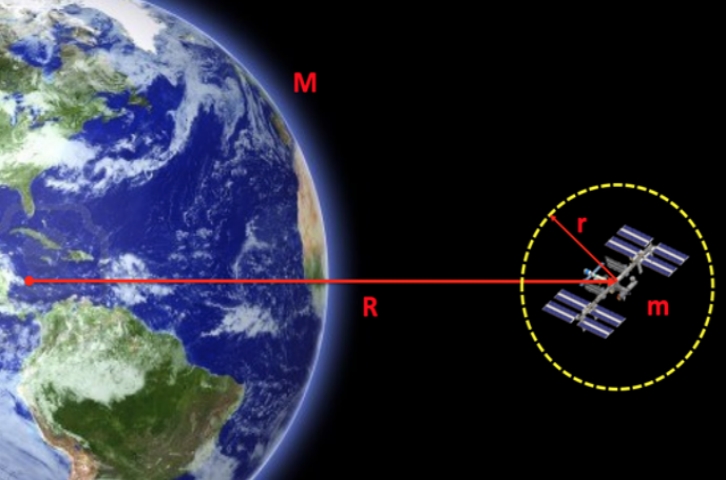
فرض کنید جرم جسمی فضایی همچون زمین برابر با $$ m $$ باشد. این جرم به دور جرمی سنگین‌تر همچون خورشید (به جرم $$ M $$) با نیم‌قطر $$ a $$ در حال حرکت است. هم‌چنین خروج از مرکز حرکت را برابر با $$ e $$ در نظر بگیرید. در این صورت شعاع هیل جسم کوچک‌تر (زمین) برابر است با:
$$ { \displaystyle r _ { \mathrm { H } } \approx a ( 1 - e ) { \sqrt[{3 \ \ } ] { \left ( \frac { m } { 3 M } \right ) } } } $$
با صرف نظر کردن از خروج از مرکز، معادله شعاع هیل به‌صورت زیر بدست خواهد آمد.
$$ { \displaystyle r _ { \mathrm { H } } \approx a { \sqrt[ { 3 \ \ } ] { \left ( \frac { m } { 3M } \right ) } } } $$
برای نمونه زمین را در نظر بگیرید. زمین به جرم $$ 5 . 9 7 × 10 ^ { 2 4 } \ k g $$ به دور خورشید به جرم $$ 1.99 × 10 ^ {30} \ kg $$ و در فاصله $$ 149.6 $$ میلیون کیلومتری در حال چرخش است. با توجه به ثابت‌ها، شعاع هیل برای زمین حدود $$1.5$$ میلیون کیلومتر بدست می‌آید. بنابراین در فاصله‌ای کمتر از این عدد، با گذشت زمان اجسام در مدار زمین قرار خواهند گرفت. برای نمونه شعاع مدار ماه برابر با $$ 0.384 $$ میلیون کیلومتر است. توجه داشته باشید که تمامی ماهواره‌های ارسال شده در مدار زمین نیز در شعاعی کمتر از شعاع هیل زمین قرار می‌گیرند. نهایتا شعاع هیل را می‌توان مطابق با نسبت بیان شده در زیر بدست آورد.
$$ { \displaystyle 3 { \frac { r_ { \mathrm { H } } ^ { 3 } } { a^ {3} } } \approx {\frac {m}{ M } } } $$
همان‌طور که می‌بینید رابطه فوق بر حسب توان سوم بدست آمده است. از این رو می‌توان گفت که این رابطه نشان‌دهنده نسبت حجم کره هیل به حجم مداری است که جسم کوچک‌تر به دور جسم بزرگ‌تر دوران می‌کند.
راه دیگری که می‌توان با استفاده از آن شعاع هیل را یافت، این است که نیروی گرانشی و نیروی مرکزگرا را برای یک جسم نمونه، برابر قرار داد. فرض کنید فاصله بین دو جسم فضایی (برای مثال زمین و خورشید) به جرم $$ m $$ و $$ M $$، برابر با $$ r $$ باشد. اگر جسم نمونه دقیقا بین دو جسم فضایی و در فاصله شعاع هیل ($$ r_H $$) از جسم کوچک‌تر دوران کند. در این صورت نیروی وارد شده به آن در نتیجه دو جسم با هم برابر خواهد بود. از این رو تعادل نیرویی را می‌توان به‌صورت زیر بیان کرد:
$$ { \displaystyle { \frac { G m } { r _ { \mathrm { H } } ^ { 2 } } } - { \frac { G M } { ( r - r _ { \mathrm { H } } ) ^ { 2 } } } + \Omega ^ { 2 } ( r -r _ { \mathrm { H } } ) =0 } $$
در رابطه فوق $$ G $$، نشان‌دهنده ثابت گرانشی بوده و $$ \Omega $$ سرعت زاویه‌ای جسم کوچک‌تر را نشان می‌دهد. مقدار این سرعت زاویه‌ای برابر است با:
$$ \large { \displaystyle \Omega = { \sqrt { \left ( \frac { G M } { r ^ { 3 } } \right ) } } } $$
توجه داشته باشید که در روابط فوق فرض $$ { \displaystyle m \ll M } $$ نیز در نظر گرفته شده است. این رابطه را می‌توان به‌صورت زیر نیز بیان کرد:
$$ { \displaystyle { \frac { m } { r _ { \mathrm { H } } ^ { 2 } } } - { \frac {M}{ r ^ { 2 } } } \left(1-{\frac { r _ { \mathrm { H } } } { r } }\right ) ^ { - 2 } + { \frac { M }{ r ^ { 2 } } } \left(1-{\frac { r _ { \mathrm { H } } } { r } } \right ) = 0 } $$
$$ \Rightarrow { \displaystyle { \frac { m } { r _ { \mathrm { H } } ^ { 2} } } - { \frac { M } { r ^ { 2 } } } \left ( 1 + 2 { \frac { r _ { \mathrm { H } } } { r } }\right)+{\frac {M}{ r ^{ 2 } } } \left(1-{\frac { r _ { \mathrm { H } } } { r } } \right)\approx {\frac {m}{ r _ { \mathrm { H } } ^ { 2 } } } - { \frac { M } { r^ {2 } } } \left ( 3 { \frac { r _ { \mathrm { H } } } { r } } \right ) \approx 0 } $$
در نتیجه نسبت شعاع کره هیل به فاصله دو جسم برابر می‌شود با:
$$ { \displaystyle { \frac { r _ { \mathrm { H } } } { r } } \approx { \sqrt [ { 3 } \ \ ] { \left ( \frac { m } { 3 M } \right ) } } } $$
توجه داشته باشید که اگر مدار جسم ثانویه به دور جسم اولیه به‌صورت بیضی باشد، در این صورت شعاع هیل در «اوج» (Apocenter) ماکزیمم است. به همین صورت همین شعاع در «حضیض» (Pericenter) نیز مینیمم است. در آینده و در مطلب معادلات کلپر در مورد این مفاهیم به‌صورتی کمی‌تر بحث خواهیم کرد.
در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
^^
