پیمایش گراهام (Graham Scan) – به زبان ساده

«پیمایش گراهام» (Graham Scan) روشی برای پیدا کردن «پوش محدب» (Convex Hull) برای یک مجموعه متناهی از نقاط موجود در صفحه است. این الگوریتم، به افتخار «رونالد گراهام» (Ronald Graham) که در سال ۱۹۷۲ الگوریتم اصلی را منتشر کرد، پیمایش گراهام نام‌گذاری شده است. الگوریتم پیمایش گراهام، همه راس‌های قرار گرفته در امتداد مرزهای پوش محدب را پیدا می‌کند. در الگوریتم پیمایش گراهام از «پشته» برای شناسایی و حذف موثر تقعرها در مرزها استفاده می‌شود. پیچیدگی زمانی این روش از درجه O(n log n)‎ است. در این مطلب، به طور کامل و به زبان ساده، به پیمایش گراهام پرداخته و پیاده‌سازی آن در «زبان برنامه‌نویسی پایتون» (Python Programming Language)، زبان C، «سی‌پلاس‌پلاس» (C++‎)، «گو» (Go)، «جاوا» (Java)، «جاوا اسکریپت» (Java Script)، «جولیا» (Julia) و «هسکل» (Haskell) انجام شده است.

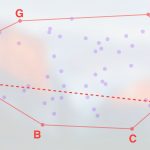
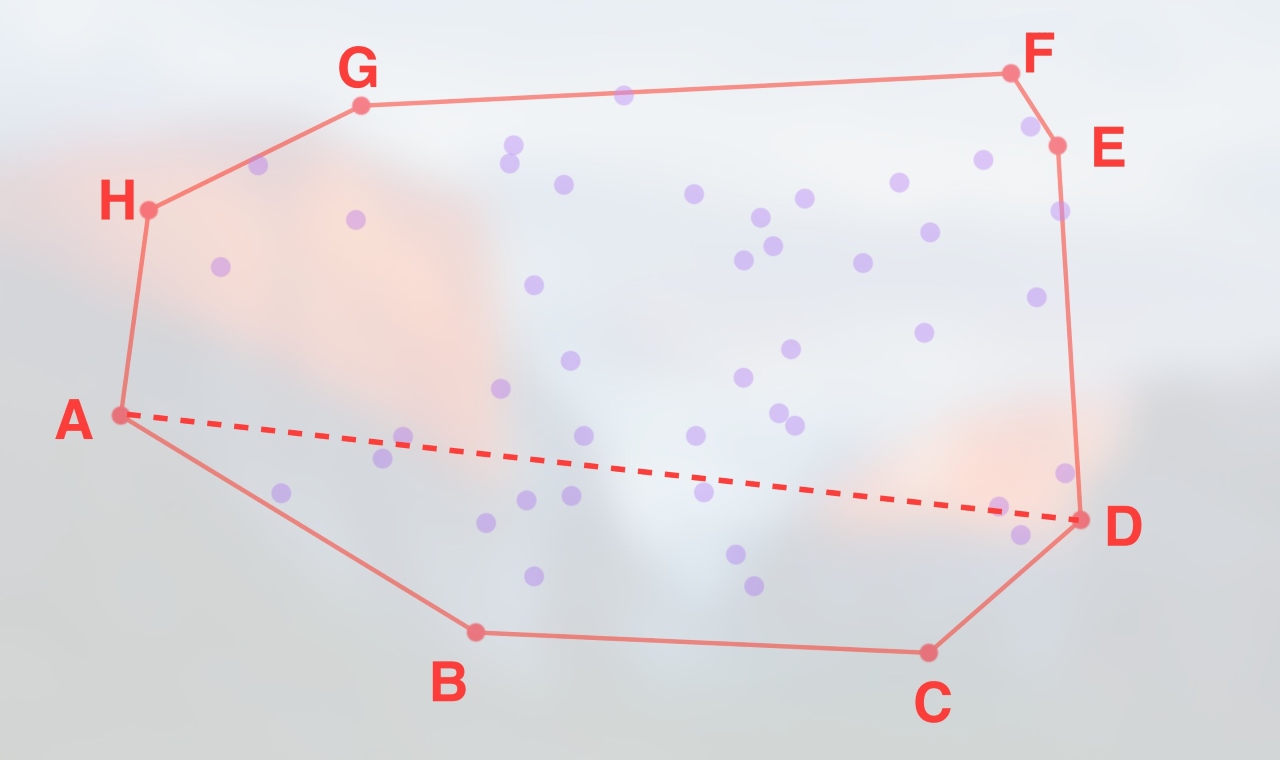
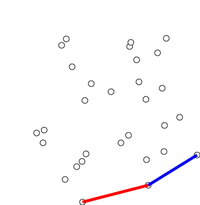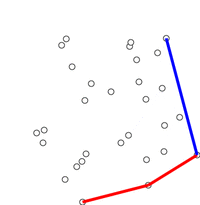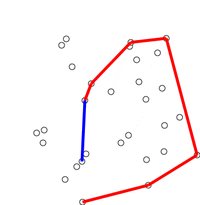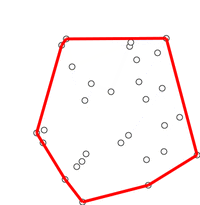
پیمایش گراهام

تقریبا به طور هم‌زمان با «جارویس مارس» (Jarvis March)، «رونالد گراهام» (R. L. Graham) نیز الگوریتمی را برای پیدا کردن پوش محدب یک مجموعه تصادفی از نقاط ارائه داد. برخلاف روش جارویس مارچ که عملیاتی از درجه O(nh)‎ است، پیمایش گراهام از مرتبه O(nlog(n))‎ است. در پیچیدگی زمانی بیان شده، n تعداد نقاط و h اندازه پوش است. این یعنی پیچیدگی پیمایش گراهام به خروجی حساس نیست. علاوه بر آن، مواردی وجود دارند که روش جارویس مارس برای حل آن‌ها بهینه‌تر است. این موضوع بستگی به اندازه پوش و تعداد نقاط قابل پوشش دارد.

در الگوریتم پیمایش گراهام، برخلاف الگوریتم جارویس مارس که کار از سمت چپی‌ترین نقطه شروع می‌شود، پیمایش از پایین آغاز می‌شود. سپس، توزیع نقاط بر مبنای زاویه بین پایین‌ترین نقطه، نقطه اصلی و هر یک از دیگر نقاط مرتب‌سازی می‌شود. پس از مرتب‌سازی، به صورت نقطه به نقطه، جستجو برای نقاط پوش محدب انجام و سایر نقاط به دور انداخته می‌شود. این کار با جستجو کردن به صورت چرخش پادساعت‌گرد انجام می‌شود. اگر زاویه بین سه نقطه، درونی شود، شکل قطعا پوش نیست. بنابراین، می‌توان این نتیجه را به دور انداخت. همچنین، می‌توان بررسی کرد که چرخش پادساعت‌گرد با توابع مثلثاتی و یا با استفاده از ضرب داخلی مانند آنچه در زیر وجود دارد است.

کد پایتون

کد C

کد ++C

کد Go

کد جاوا

کد جاوا اسکریپت

کد جولیا

کد هسکل

اگر خروجی این تابع ۰ باشد، نقاط خطی هستند. اگر خروجی مثبت باشد، نقاط یک چرخش چپ پادساعت‌گرد را شکل می‌دهند. اگر خروجی منفی باشد، نقاط یک چرخش راست ساعت‌گرد را شکل می‌دهند. اساسا، چرخش ساعت‌گرد مد نظر نیست، زیرا این به معنای قرار داشتن در زاویه داخلی است.

فیلم آموزش الگوریتم های مرتب سازی در زبان برنامه نویسی پایتون با مثال (رایگان) در فرادرس

کلیک کنید

برای کاهش مصرف حافظه و اجتناب از عملیات پرهزینه append()‎، در نهایت جستجو برای نقاطی که باید روی پوش باشند انجام می‌شود و آن‌ها با اولین عناصر موجود در آرایه جا به جا می‌شوند. اگر M عنصر روی پوش وجود داشته باشند، M عنصر اول در توزیع تصادفی خروجی نقاط، پوش خواهند بود. در پایان، کد باید به صورت زیر باشد.

کد پایتون

کد C

کد ++C

کد Go

کد جاوا

کد جاوا اسکریپت

کد جولیا

کد هسکل

نمونه کد پیمایش گراهام در پایتون

نمونه کد پیمایش گراهام در C

نمونه کد پیمایش گراهام در ++C

نمونه کد پیمایش گراهام در Go

نمونه کد پیمایش گراهام در جاوا

نمونه کد پیمایش گراهام در جاوا اسکریپت

نمونه کد پیمایش گراهام در جولیا

نمونه کد پیمایش گراهام در هسکل

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌‌نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• رنگ‌آمیزی گراف به روش حریصانه — به زبان ساده

^^