دنباله هندسی و مجموع آن — به زبان ساده

در این مطلب از مجله فرادرس همانطور که از عنوان آن بر می‌آید به مبحث دنباله هندسی می‌پردازیم و مثال‌هایی را نیز پیرامون همین موضوع عنوان خواهیم کرد.

دنباله چیست؟

به رشته ای از اعداد که پشت سر هم نوشته می شوند، دنباله عددی گفته می‌شود. به هر کدام از اعداد این دنباله، یک جمله گفته می‌شود. اعداد و یا به عبارتی جملات یک دنباله ممکن است با هم ارتباط داشته باشند یا نداشته باشند. اولین جمله دنباله را با a₁ و دومی را با a₂ و در نهایت جمله n-اُم را با a_n نشان می دهیم که n شماره جمله دنباله است و همواره یک عدد طبیعی است.

اگر بین جملات دنباله رابطه‌ای وجود داشته باشد، به این رابطه الگوی دنباله گفته می‌شود. بنابراین الگوی دنباله، رابطه‌ای است بین شماره جملات (1,2,3,4,.. ) و جملات (..., a₁ ,a₂). به فرم کلی این الگو، جمله عمومی میگویند و با نماد (a_n) نشان داده می‌شود.

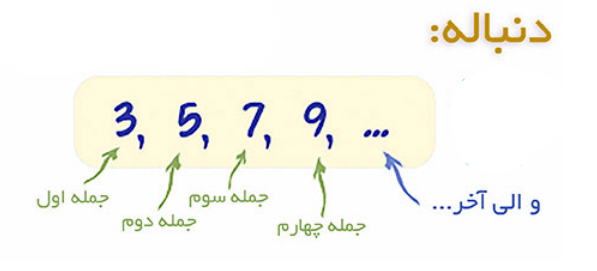
همان‌گونه که در دنباله بالا مشاهده می‌کنید، فاصله اعداد آن مقداری ثابت است. به این نوع از دنباله اصطلاحا تصاعد حسابی گفته می‌شود.

دنباله هندسی

در یک دنباله هندسی هر جمله به وسیله ضرب یک عدد ثابت در عدد قبلی به دست می آید.

مثال:

2, 4, 8, 16, 32, 64, 128, 256, ...

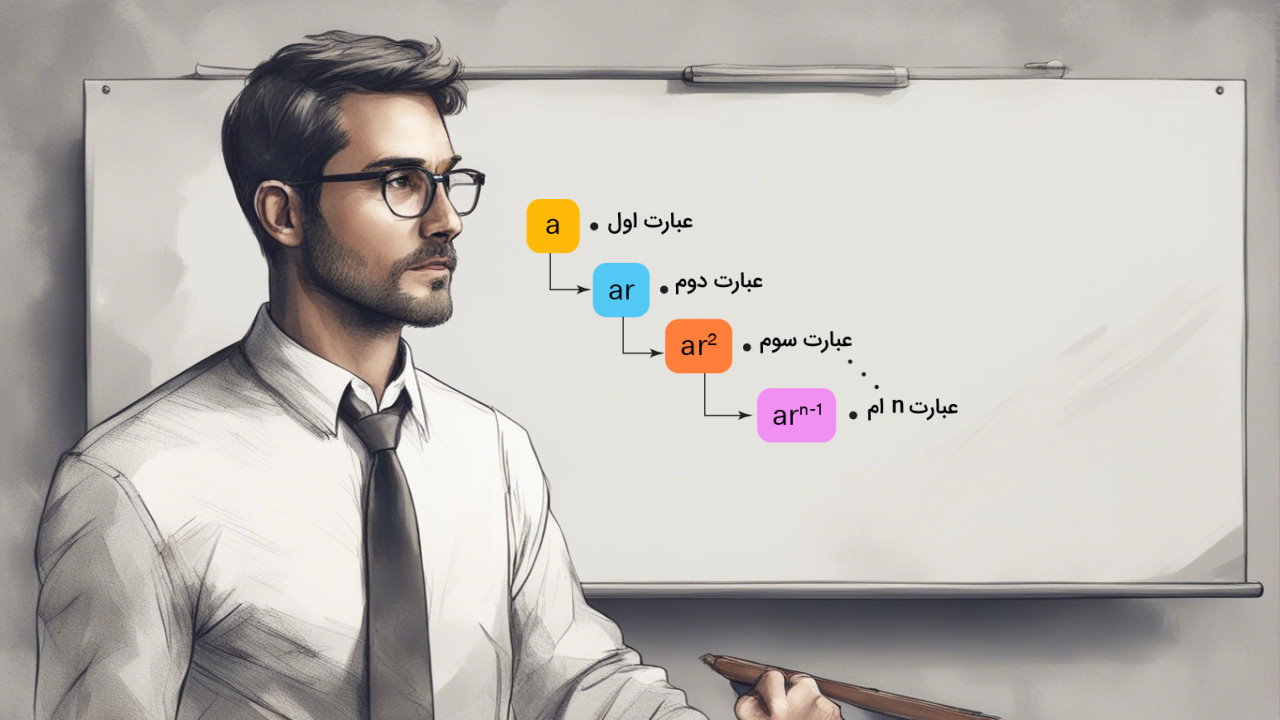
دنباله فوق، مضربی از 2 بین هر عدد دارد. هر جمله، به جز جمله اول به وسیله ضرب عدد قبلی در 2 به دست می‌آید. به طور کلی ما یک دنباله هندسی را به این شکل می‌نویسیم:

{a, ar, ar², ar³, ...}

که:

• a اولین جمله است، و
• r مضرب بین جملات است که به نام «قدر نسبت» نامیده می‌شود.

مثال:

{ 1, 2, 4, 8, ... }

دنباله از 1 شروع می شود و در هر مرحله دو برابر می شود، پس

• a = 1 اولین جمله است.
• r = 2 «قدر نسبت» بین جملات باعث دو برابر شدن جمله بعدی می شود.

و داریم:

{a, ar, ar², ar³, ... }

= {1, 1×2, 1×2², 1×2³, ... }

= {1, 2, 4, 8, ...}

اما باید توجه داشته باشید که r نمی‌تواند 0 باشد:

• اگر r = 0 دنباله ما به شکل { ... ,0 ,0 ,a} در می‌آیند که یک دنباله هندسی نیست.

ضابطه

به الگوی کلی جملات یک دنباله، ضابطه آن دنباله گفته می‌شود. بنابراین از روی ضابطه یک دنباله می‌توان هر جمله آن را به دست آورد.

فرمول یافتن جمله n-ام یک دنباله هندسی به صورت زیر است:

X_n = ar^(n-1)

دلیل این که از n-1 استفاده می‌کنیم، ابن است که ar⁰ برای جمله اول است.

مثال:

10, 30, 90, 270, 810, 2430, ...

این دنباله در بین جملات خود از مضرب 3 استفاده کرده است.

مقادیر a و r برابرند با:

• a = 10 (اولین جمله)
• r = 3 (قدر نسبت)

ضابطه این دنباله به صورت زیر است:

xⁿ = 10 × 3^(n-1)

پس، جمله چهارم برابر است با:

x₄ = 10 × 3^(4-1) = 10 × 3³ = 10 × 27 = 270

و جمله دهم برابر است با:

x₁₀ = 10 × 3^(10-1) = 10 × 3⁹ = 10 × 19683 = 196830

از طرفی باید بدانیم که همه دنباله‌ها به صورت صعودی نیستند و دنباله های نزولی نیز وجود دارند. به عبارت دیگر در یک دنباله هندسی ممکن است رفته‌رفته اندازه هر جمله کمتر شود:

مثال:

4, 2, 1, 0.5, 0.25, ...

این دنباله مضربی از 0.5 بین جملات خود دارد.

و ضابطه آن برابر است با:

x_n = 4 × (0.5)^n-1

چرا به این نوع دنباله، دنباله «هندسی» گفته می‌شود؟

دلیل این که این نوع دنباله ، هندسی نامیده می‌شود این است که حملات دنباله با ترتیبی همانند افزایش ابعاد در هندسه بسط می‌یابند.

برای مثال:

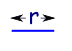 یک خط «یک بعدی» است و طول آن برابر با  r است.

 در «دو بعد» قرار دارد و یک مربع با مساحتی برابر با r2 است.

 در «سه بعد» قرار دارد و مکعبی با  حجم r3 است.

و این فهرست به همین ترتیب ادامه دارد. باید توجه داشته باشید که در  ریاضیات، می‌توانیم 4 بعد یا بیشتر نیز داشته باشیم. همچنین به خاطر بسپارید که به دنباله های هندسی، گاهی اوقات «تصاعد» هندسی نیز گفته می‌شود.

 جمع کردن یک سری هندسی

هنگامی که نیاز به جمع کردن یک دنباله هندسی داریم، یک فرمول برای این کار وجود دارد.

برای جمع کردن:

a + ar + ar² + ... + ar^(n-1)

هر جمله برابر ar^k است که k از صفر شروع می شود و تا n-1 پیش می رود. به طور کلی می‌توانید از این فرمول استفاده کنید:

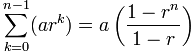
در رابطه فوق، a اولین جمله است. r برابر «قدر نسبت» بین جملات است و n نیز تعداد جملات است. شاید از خود بپرسید این علامت جالب چیست؟ به علامت Σ ، «نماد سیگما» گفته می‌شود که به معنی «جمع کردن» است. در زیر و بالای این نماد مقدار‌های آغازی و پایانی سری جمع مشخص شدهاند:

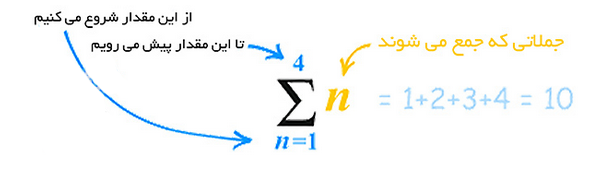
معنی نماد فوق این است که n ها را با هم جمع کنید، به طوری که n از 1 تا 4 باشد. و پاسخ آن نیز برابر با 10 است. این فرمول استفاده آسانی دارد. فقط کافی است مقادیر a، r و n را مشخص کنیم.

مثال: 4 جمله اول این دنباله را جمع کنید.

10, 30, 90, 270, 810, 2430, ...

این دنباله مضرب 3 بین جملات خود دارد.

مقادیر a, r و n برابرند با:

• a = 10 (جمله اول)
• r = 3 (قدر نسبت)
• n = 4 (می خواهیم 4 جمله اول را با هم جمع کنیم)

پس:

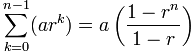
که داریم:

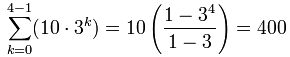
خودتان می‌توانید صحت را بررسی نمایید:

10 + 30 + 90 + 270 = 400

جمع کردن عادی مقدار جملات در مثال فوق آسان بود، چرا که تنها 4 جمله را جمع کردیم؛ اما فرض کنید به جمع کردن 50 جمله نیاز بود. در این صورت می‌بینیم که استفاده از فرمول روشی بسیار آسان‌تر است.

استفاده از فرمول

مثال: دانه‌های برنج روی یک صفحه شطرنج

فرض کنید روی یک صفحه شطرنج به ترتیب زیر دانه برنج قرار می‌دهیم:

• 1 دانه در مربع اول
• 2 دانه در مربع دوم
• 4 دانه در مربع سوم
• ...

یعنی در هر مربع دو برابر دانه‌های خانه قبلی، دانه قرار دهیم. اینک سوال این است که  کلا چند دانه برنج روی صفحه داریم؟ در این مثال روابط زیر برقرار هستند:

• a = 1 (جمله اول)
• r = 2 (در هر مرحله دو برابر می شود)
• n = 64 (چون 64 مربع روی یک صفحه شطرنج وجود دارد)

پس:

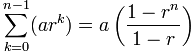
و داریم:

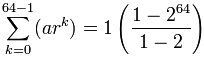
= (1 - 2⁶⁴) / ( - 1) = 2⁶⁴ - 1

= 18,446,744,073,709,551,615

همان طور که می‌بینید مجموع دانه‌های برنج عدد بسیار بزرگی است. برای این که به بزرگی این عدد بهتر پی ببرید اشاره می‌کنیم که هر کیلو برنج تقریباً 50،000 عدد برنج است. با تقسیم عدد فوق بر این مقدار به عدد 368،934،881،474 تن دست می‌یابیم. باز برای این که بتوانید تصور بهتری داشته باشید باید بیان کنیم که مصرف کل برنج ایران، سالانه 3،200،000 تن است. یعنی با برنج‌هایی که بر اساس دنباله هندسی فوق روی صفحه شطرنج قرار دادیم، می‌توانیم مصرف برنج 115،292 سال ایران را تامین کنیم!

برای یادگیری بهتر به یک مثال دیگر توجه کنید. این بار قدر نسبت تصاعد هندسی را کوچکتر از 1 در نظر گرفته‌ایم:

{ ¹/₂, ¹/₄, ¹/₈, ¹/₁₆, ...}

مقادیر a, r و n برابرند با:

• a = ¹/₂ (جمله اول)
• r = ¹/₂ (در هر مرحله جملات نصف می شوند)
• n = 10 (ده جمله را جمع می کنیم)

پس:

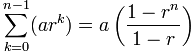
و داریم:

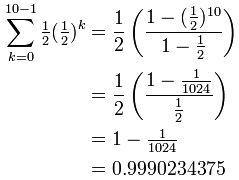
می‌بینیم که نتیجه بسیار به 1 نزدیک است. سوالی که پیش می‌آید این است که اگر به افزایش تعداد n ادامه دهیم، چه اتفاقی می‌افتد؟

آیا فرمول درست کار می‌کند؟

برای این که ببینیم چرا فرمول درست کار می‌کند، از یک ترقیند جالب استفاده می‌کنیم که ارزش شناختنش را دارد.

ابتدا، جمع کل را یادداشت می‌کنیم و آن را S می‌نامیم:

S = a + ar + ar² + ... + ar^(n-2)+ ar^(n-1)

سپس، S را در r ضرب می‌کنیم:

S·r = ar + ar² + ar³ + ... + ar^(n-1) + arⁿ

دقت کنید که S و S.r شبیه هم هستند. اکنون آنها را از هم تفریق کنید.

جالب است. می بینیم که تمام جملات میانی کاملا حذف شدند و این همان ترفندی بود که در ابتدای این بخش از آن صحبت کردیم. با تفریق S.r از S نتیجه ساده زیر به دست می‌آید:

S - S.r = a - arⁿ

ترتیب را طوری می‌چینیم که S را پیدا کنیم:

از S و a فاکتورگیری می‌کنیم:

S (1 - r) = a (1 - rⁿ)

سپس بر 1 منهای r تقسیم می‌کنیم:

S = a(1 − rⁿ) / (1 − r)

می‌بینیم که همان فرمول جمع دنباله به دست آمده است.

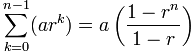
سری‌های هندسی نامتناهی

شاید از خود بپرسید اگر n تا بی‌نهایت پیش برود، چه اتفاقی می افتد.

هنگامی که r کمتر از 1 باشد، rⁿ به سمت صفر می‌رود و داریم:

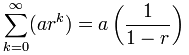
توجه داشته باشید که اگر r بزرگتر یا مساوی 1 باشد (یا کمتر از 1- باشد) این فرمول صادق نیست. r باید بین 1 و 1- باشد و شامل خود این اعداد نباشد و همچنین r نباید 0 باشد چون دنباله ما به شکل زیر خواهد بود که هندسی نیست:

{ a, 0, 0, ... }

بیایید مثال قبلی را بررسی کنیم و ببینیم چه می‌شود:

مثال: تمامی عضو‌های دنباله هندسی که در هر مرحله نصف می‌شود را با هم جمع کنید:

{ ¹/₂, ¹/₄, ¹/₈, ¹/₁₆, ... }

داریم:

• a = ¹/₂ (جمله اول)
• r = ¹/₂ (در هر مرحله نصف می شود)

پس:

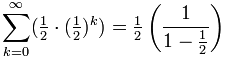
= ¹/₂ × 1 / ¹/₂ = 1

می‎بینیم  که مجموع این اعداد دقیقاً برابر با 1 است. برای درک بهتر این مجموع به مربع زیر نگاه کنید:

از طریق جمع  ¹/₂, ¹/₄, ¹/₈, ¹/₁₆, ... یک مربع تشکیل می‌شود.

اعداد اعشاری با دوره گردش

آیا ...0.999 برابر با 1 است؟ برای پاسخ به این سوال، از فرمول معروف خود استفاده می‌کنیم.

مثال: مقدار ...0.999 را حساب کنید

می توانیم اعداد اعشاری با دوره گرد را به شکل زیر بنویسیم:

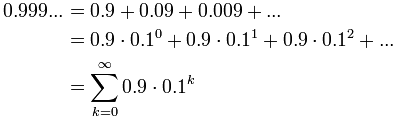
و اکنون می توانیم از فرمول استفاده کنیم:

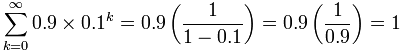
بدین ترتیب می‌بینیم که 0.999 با 1 برابر است. در این نوشته مشاهده کردیم که دنباله های هندسی و مجموع آن‌ها، انواع کارهای عالی و سخت را به خوبی انجام می‌دهند.