متغیر تصادفی و توزیع هندسی — به زبان ساده

دنباله‌ای از آزمایش‌های تصادفی برنولی مستقل از یکدیگر را در نظر بگیرید که احتمال موفقیت برای هر یک ثابت و برابر با $$p$$ باشد. اگر متغیر تصادفی $$X$$ را تعداد آزمایش‌ها برای رسیدن به اولین موفقیت در نظر بگیریم، این متغیر تصادفی دارای توزیع احتمال با نام «هندسی» (Geometric) خواهد بود. پس بین آزمایش برنولی و متغیر تصادفی و توزیع هندسی ارتباطی وجود دارد.

برای مثال فرض کنید پزشکی در یک روستا به معاینه مردم می‌پردازد تا به اولین نشانه بیماری دیابت برسد. احتمال شیوع بیماری دیابت از قبل برآورد شده و برابر با $$p$$‌ است. شانس اینکه پزشک با معاینه نفر ۵ام به نشانه‌های دیابت برخورد کند از توزیع هندسی قابل محاسبه است.

در این حالت احتمال مشاهده اولین موفقیت در اولین پرتاب، دومین پرتاب و ... را می‌توان محاسبه کرد. پس مجموعه مقدارها یا تکیه‌گاه این متغیر تصادفی به صورت $$x=1,2,\ldots$$ خواهد بود. در نتیجه این متغیر تصادفی نیز به مانند متغیر تصادفی برنولی و دو جمله‌ای از نوع گسسته است، با این تفاوت که جامعه آماری که توسط متغیر تصادفی هندسی توصیف می‌شود، نامتناهی است.

برای آشنایی با توزیع‌های آماری و خصوصیات آن‌ها نوشتار توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس را مطالعه فرمایید. همچنین خواندن توزیع های گسسته آماری و رابطه بین آنها — به زبان ساده نیز خالی از لطف نیست.

متغیر تصادفی و توزیع هندسی

همانطور که اشاره شد، متغیر تصادفی هندسی تعداد تکرارهای آزمایش تا رسیدن به اولین موفقیت در یک دنباله از آزمایش‌های تصادفی برنولی است. برای تاکید بیشتر و مشخص شدن خصوصیاتی که باید تکرار آزمایش برنولی داشته باشند، به نکات زیر اشاره می‌کنیم:

• دنباله آزمایش‌های تصادفی باید مستقل از یکدیگر باشند.
• دنباله آزمایش‌های تصادفی باید از نوع برنولی باشند.
• پارامترهای دنباله آزمایش‌های برنولی باید ثابت باشند.

فیلم آموزش تئوری احتمالات در فرادرس

کلیک کنید

با توجه به تعریف این متغیر تصادفی، فرم تابع احتمال یا جرم احتمال آن به صورت زیر است:

$$\large P(X=x)=p(1-p)^{x-1}=pq^{x-1}\;\;\;\;\,x=1,2,\ldots$$

در این حالت می‌نویسیم $$X\sim Ge(p)$$ و می‌خوانیم X دارای توزیع هندسی با پارامتر p است.

نکته: براساس تصاعد هندسی داریم:

$$\large \sum_{x=1}^{\infty}p(1-p)^{x-1}=1$$

البته گاهی ممکن است تعریف متغیر تصادفی هندسی را به صورت تعداد شکست‌های لازم برای رسیدن به اولین موفقیت در نظر گرفت. در این حالت اگر $$Y$$ تعداد شکست‌های لازم برای رسیدن به اولین موفقیت در نظر گرفته شود،  تکیه‌گاه $$Y$$ برابر با $$y=0,1,2,3,\ldots$$ و تابع احتمال آن به صورت زیر درخواهد آمد.

$$\large P(Y=y)=p(1-p)^{y}=pq^{y}\;\;\;\;\,y=0,1,2,\ldots$$

به این ترتیب بین دو متغیر تصادفی X و Y‌ رابطه X=Y+1 برقرار است.

مثال ۱

فرض کنید سکه سالمی را تا مشاهده اولین شیر پرتاب می‌کنیم. اگر تعداد پرتاب‌ها به عنوان متغیر تصادفی در نظر گرفته شوند،‌ تابع احتمال به فرم توزیع هندسی با پارامتر $$\frac{1}{2}$$ است و احتمال اینکه در دومین پرتاب شیر مشاهده کنیم به صورت زیر محاسبه می‌شود.

$$\large P(X=x)=\tfrac{1}{2}(1-\tfrac{1}{2})^{2-1}=0.25$$

اگر برای چنین حالتی مقدار احتمال را برای تکیه‌گاه متغیر تصادفی ترسیم کنیم، نموداری مانند تصویر ۱ ایجاد می‌شود که برای احتمال موفقیت $$p=0.5$$ نقاط با رنگ بنفش مشخص شده‌اند. این نمودار شبیه تابع نمایی با پایه کوچکتر از یک است.

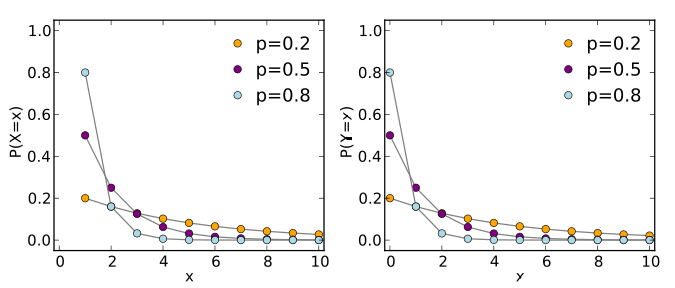
در نمودارهای تصویر ۱، مقدار متغیر تصادفی در محور افقی و مقدار احتمال در محور عمودی رسم شده است. همینطور نقاط با استفاده از یک خط به هم متصل شده تا شکل منحنی توزیع هندسی نیز نمایش داده شود. در سمت راست تصویر ۱،‌ با توجه به تکیه‌گاه متغیر تصادفی، منحنی مربوط به احتمال متغیر تصادفی هندسی به فرم Y (تعداد شکست‌ها) نمایش داده شده و در سمت چپ نیز تابع احتمال برای متغیر تصادفی هندسی به فرم X (تعداد آزمایشات) دیده می‌شود.

باید توجه داشت که با افزایش p شیب این منحنی نیز بیشتر خواهد شد.

میانگین و واریانس متغیر تصادفی هندسی

با توجه به تعریفی که برای متغیر تصادفی هندسی ارائه شد، امید-ریاضی و واریانس آن را محاسبه می‌کنیم.

برای محاسبه امید-ریاضی کافی است که مجموع حاصل‌ضرب مقدار متغیر تصادفی را در احتمال رخداد آن بدست آوریم. این کار در واقع محاسبه میانگین وزنی برای مقدارهای متغیر تصادفی با وزنی برابر با احتمال‌شان است. بنابراین اگر $$X\sim Ge(p)$$، امید-ریاضی برای آن به صورت زیر محاسبه می‌شود:

$$\large E(X)=\sum_{x=1}^{\infty}(xpq^{x-1})=p\sum_{x=1}^{\infty}(xq^{x-1})=\dfrac{p}{(1-q)^2}=\dfrac{p}{p^2}=\dfrac{1}{p}$$

زیرا براساس $$q<1$$ در تصاعد هندسی داریم:

$$\large \sum_{x=1}^{\infty}xq^{x-1}=\dfrac{1}{(1-q)^2}$$

به همین شکل برای محاسبه واریانس متغیر تصادفی هندسی براساس شکل‌های مختلف تصاعد هندسی داریم:

$$\large V(X)=E(X^2)-E^2(X)=\dfrac{1-p}{p^2}$$

ولی اگر مبنای تابع احتمال متغیر تصادفی هندسی را Y=X-1 قرار دهیم امید-ریاضی و واریانس به صورت زیر در خواهد آمد:

$$\large E(Y)= \dfrac{(1-p)}{p}$$

$$\large V(Y)=\dfrac{1-p}{p^2}$$

مثال ۲

احتمال برخورد گلوله تانک به هدف طبق ادعای کارخانه سازنده، 0.65 است. متخصص تانک باید به طور متوسط 1.54 بار (حدود ۲ بار) شلیک کند تا یکبار به هدف بزند. زیرا:

$$\large E(X)=\dfrac{1}{p}=\dfrac{100}{65}=1.54$$

مثال ۳

فیوز برق در 5٪ اوقات درست عمل نمی‌کند. پس اگر صحیح عمل نکردن فیوز را به عنوان موفقیت در نظر بگیریم، شانس موفقیت 0.05 است. احتمال اینکه فیوز پس از ۱۰۰ بار استفاده خراب شود، به صورت زیر محاسبه می‌شود:

در این حالت باید ۱۰۰ بار از فیوز استفاده کنیم تا شاهد خرابی آن باشیم، پس داریم $$X\sim Ge(0.05)$$ و باید $$P(X=100)$$ را محاسبه کنیم.

$$\large P(X=100)=pq^{99}=(0.05)(0.95)^{99}=3 \times 10^ {-4}$$

مثال ۴

اگر احتمال شیوع بیماری دیابت طبق برآوردهای انجام شده برابر با ۱٪ باشد، در یک روستا، پزشک باید به طور متوسط چند نفر را معاینه کند تا به اولین نشانه دیابت برخورد کند؟

با توجه به تعریف مسئله مشخص است که تعداد معاینات تا برخورد با اولین نشانه دیابت از توزیع هندسی با پارامتر 0.01 برخوردار است. پس داریم $$X\sim Ge(0.01)$$ است. برای پاسخ به پرسش نیز کافی است که امید-ریاضی X را محاسبه کنیم. با توجه به $$p=0.01$$ مشخص است که امید-ریاضی مقدار $$\dfrac{1}{0.01}=100$$ محاسبه خواهد شد. با توجه به نتیجه به دست آمده حال می‌توان گفت که پزشک باید به طور متوسط 100 نفر را معاینه کند تا به اولین فرد بیمار برخورد کند.

نکته: همه این مثال‌ها برحسب تعداد آزمایش‌ها تا رسیدن به اولین موفقیت نوشته شده. بنابراین از رابطه تابع چگالی که برای $$X$$ معرفی کردیم، بهره برده‌ایم.

خاصیت عدم حافظه برای متغیر تصادفی هندسی

اگر رابطه زیر برقرار باشد، متغیر تصادفی X یا توزیع متغیر تصادفی دارای خاصیت عدم حافظه است:

$$\large P(X\ge t+s|X\ge t)=P(X\ge s)$$

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

اگر X را طول عمر یک دستگاه تا خرابی در نظر بگیریم،‌ این تساوی به این معنی است که چنانچه بدانیم دستگاه تا زمان t خراب نشده، احتمال اینکه s زمان دیگر هم کار کند، مستقل از طول عمر گذشته‌اش است.

می‌توان اثبات کرد که متغیر تصادفی هندسی دارای خاصیت عدم حافظه است.

مثال ۵

با توجه به مثال ۴ اگر بدانیم پزشک با معاینه ۵ مریض به بیماری دیابت برخورد نکرده است،‌ احتمال اینکه مراجعین تا نفر هفتم دچار بیماری دیابت نشده باشند چقدر است؟

از آنجایی که متغیر تصادفی معرفی شده در مثال ۴ هندسی بوده و خاصیت عدم حافظه دارد، کافی است که براساس تعریف تابع توزیع احتمال و مکمل پیشامدها، محاسبات زیر را انجام دهیم:

$$\large P(X\geq 8|X\geq 5)=P(X\geq 5+3|X\geq 5)=P(X\geq 3)=1-P(X<3)=1-P(X\leq 2)=$$

$$\large 1\;-\;(P(X\;=\;1)+P(X\;=\;2))=1\;-\;(\;0.0099\;+\;0.0098\;)=1\;-\;0.0197=\;0.9803$$

اگر مطلب بالا برای شما مفید بوده است، احتمالاً آموزش‌هایی که در ادامه آمده‌اند نیز برایتان کاربردی خواهند بود.

• مجموعه آموزش های برنامه نویسی متلب برای علوم و مهندسی
• متغیر های تصادفی – میانگین، واریانس و انحراف معیار – به زبان ساده
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش آمار و احتمال مهندسی
• متغیر تصادفی و توزیع برنولی --- به زبان ساده
• متغیر تصادفی و توزیع دو جمله‌ای --- به زبان ساده

^^