اطلاع فیشر (Fisher Information) – مفاهیم و کاربردها

یکی از مباحثی که از دستاوردهای آمارشناس و ریاضی‌دان بزرگ «رونالد فیشر» (Ronald Fisher) محسوب می‌شود، «اطلاع فیشر» (Fisher Information) یا به اختصار «اطلاع» (Information) است. براساس این نظریه، می‌توان مقدار اطلاعاتی را اندازه‌گیری کرد که یک نمونه تصادفی برای شناخت از پارامتر نامعلوم جامعه ($$\theta$$) در خود دارد. حتی می‌توان به نوعی میزان «اطلاع فیشر» را حساسیت تابع درستنمایی نسبت به تغییرات پارامتر در نظر گرفت.

برای آشنایی با مباحث مطرح شده در این نوشتار، بهتر است مطالب تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده و امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتار متغیر تصادفی و توزیع برنولی — به زبان ساده و توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها نیز خالی از لطف نیست.

اطلاع فیشر (Fisher Information)

مفهوم و نحوه محاسبه «اطلاع فیشر» توسط بسیاری از آمارشناسان از جمله «پیرسون» (Pearson) و «فیلون» (Filon) مورد بررسی و تحقیق قرار گرفت. ولی این آمارشناس آمریکایی «فیشر» (Fisher) بود که با ابداع «برآوردگر حداکثر درستنمایی» (Maximum Likelihood Estimator) و ارتباط دادن آن با اطلاع فیشر، در نظریه آمار دست به ابتکار زد. براساس اطلاع فیشر می‌توان میزان اطلاعاتی را که مشاهدات یک متغیر تصادفی در مورد پارامتر نامعلوم جامعه در خود دارند، اندازه‌گیری کرد. فرض کنید تابع توزیع احتمال یا تابع چگالی احتمال برای متغیر متغیر تصادفی $$X$$ به صورت $$f_X(x;\theta)$$ نشان داده شود. این تابع به نوعی احتمال مشاهده X را با معلوم بودن پارامتر $$\theta$$ محاسبه می‌کند.

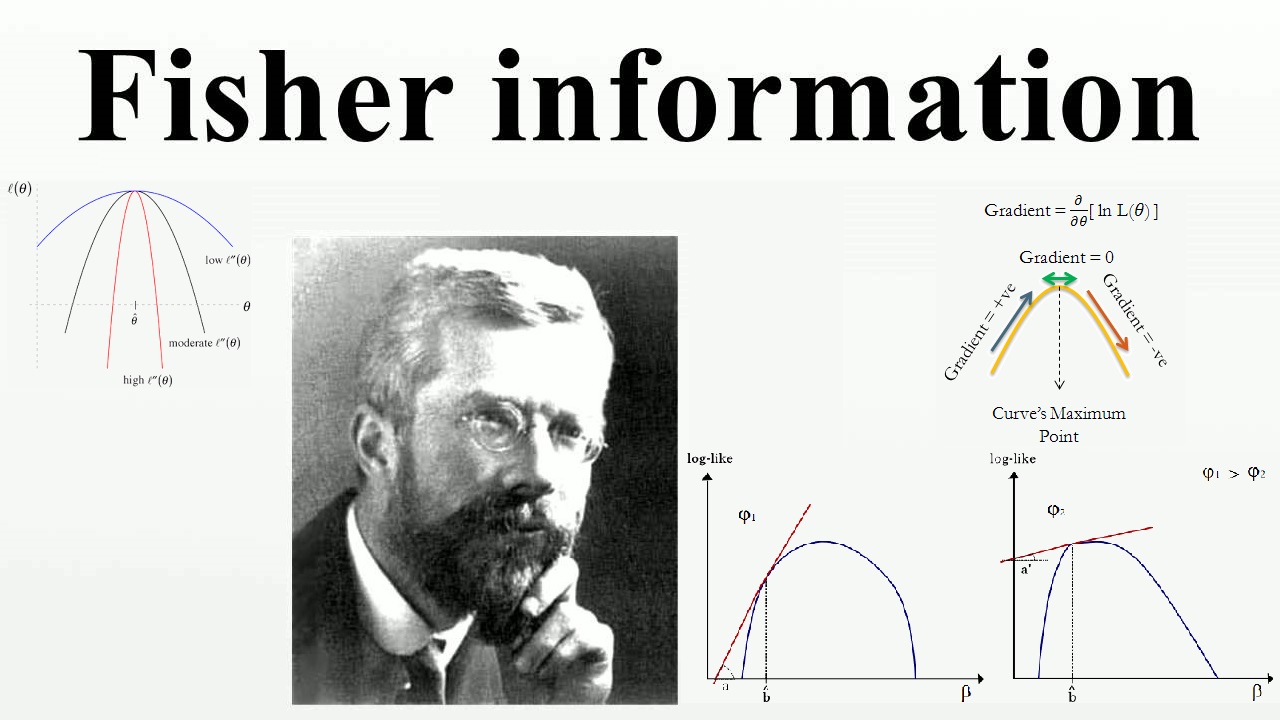
حال اگر پارامتر جامعه را به صورت یک متغیر تصادفی در نظر بگیریم، این تابع چگالی به صورت یک تابع چگالی شرطی در خواهد آمد. در این حالت اگر مشاهدات، موجود فرض شوند، این تابع را یک «تابع درستنمایی» (Likelihood Function) محسوب می‌کنند. اگر این تابع براساس تغییرات $$\theta$$ به عنوان متغیر رسم شود و منحنی دارای یک قله (حداکثر مقدار) باشد، می‌توان نتیجه گرفت که مشاهدات از مقادیر $$X$$ می‌توانند برآوردگر خوبی برای پارامتر جامعه $$\theta$$ باشند. پس داده‌ها و مقادیر مشاهده شده از متغیر تصادفی $$X$$ دارای اطلاعات زیادی در مورد پارامتر جامعه هستند.

برعکس، اگر تابع درستنمایی به صورت گسترده و پهن باشد، می‌توان نمونه‌های زیادی مانند $$X$$ داشت که برآوردگر مناسب برای پارامتر $$\theta$$ باشند، پس به نظر می‌رسد که $$X$$ اطلاع زیادی از پارامتر نخواهد داشت.

نکته: توجه داشته باشید که در اینجا فرض بر این است که مقادیر متغیر تصادفی مشاهده شده‌اند و هدف تعیین تغییرات پارامتر است. برای اندازه‌گیری میزان تغییرات تابع درستنمایی نسبت به پارامتر نیز از مشتق تابع درستنمایی نسبت به پارامتر استفاده خواهیم کرد.

مفهوم اطلاع فیشر

با توجه به توضیحات قبلی، این طور به نظر می‌رسد که لازم است، واریانس تغییرات تابع درستنمایی (یا تابع یکنوای از آن) را برحسب نمونه‌های تصادفی، اندازه‌گیری کنیم. از طرفی می‌دانیم که تغییرات یک تابع نسبت به متغیر توسط مشتق آن تابع شناخته شده و تعیین می‌شود.

مشخص است که مقدار اطلاعاتی که نمونه‌های تصادفی در اختیارمان قرار می‌دهند، متفاوت است. در ادامه خواهیم دید که متوسط این تغییرات به ازای نمونه‌های مختلف (امید ریاضی مشتق تابع درستنمایی) برابر با صفر خواهد بود. پس باید مشخص کنیم که پراکندگی تغییرات تابع درستنمایی برای نمونه‌های مختلف چقدر است. به این ترتیب از واریانس به عنوان معیار مقایسه استفاده خواهیم کرد. همانطور که در نوشتار مربوط به امید ریاضی خوانده‌ایم، می‌دانیم که برای پیدا کردن واریانس یک متغیر تصادفی باید از رابطه زیر کمک گرفت.

$$\large \operatorname{Var}(X)=\operatorname{E}(X^2)-\operatorname{E}^2(X)$$

رابطه ۱

البته از آنجایی که در اکثر مواقع تابع درستنمایی به شکل نمایی نوشته شده است، استفاده از عملگر لگاریتم تاثیری در تعیین رفتار تابع درستنمایی نخواهد داشت. پس عمل مشتق‌گیری را بر روی لگاریتم تابع درستنمایی انجام خواهیم داد و سپس واریانس تابع حاصل را برحسب نمونه‌های تصادفی محاسبه می‌کنیم.

$$\large \operatorname{Var}({\frac {\partial }{\partial \theta }}\log f(X;\theta ))$$

اغلب به مشتق لگاریتم تابع درستنمایی، «تابع امتیاز» (Score Function)، می‌گویند که حساسیت تابع درستنمایی را به پارامتر تعیین می‌کند. به این ترتیب مشخص است که واریانس تابع امتیاز، همان اطلاع فیشر خواهد بود.

با توجه به رابطه ۱ و مفهوم اطلاع فیشر خواهیم داشت:

$$\large \operatorname{Var}({\frac {\partial }{\partial \theta }}\log f(X;\theta ))=\operatorname{E}\Big({\frac {\partial }{\partial \theta }}\log f(X;\theta )\Big)^2-\operatorname{E^2}\Big ({\frac {\partial }{\partial \theta }}\log f(X;\theta )\Big)$$

برای شروع کار بهتر است اصطلاح شرایط نظم را شرح دهیم، زیرا اطلاع فیشر براساس «شرایط نظم» (Regularity Condition) راحت‌تر محاسبه می‌شود.

شرایط نظم (Regularity Condition)

همانطور که دیدید، برای ساده‌تر کردن و انجام محاسبات مربوط به اطلاع فیشر از شرایط نظم اسم برده شد. در این قسمت به معرفی شرایط نظم خواهیم پرداخت. این شرایط را مطابق فهرست زیر می‌شناسیم.

• پارامتر مجهول ($$\theta$$) یک فاصله باز از اعداد حقیقی است. ($$\theta \in \Theta \subset R$$)
• مشتق تابع چگالی احتمال متغیر تصادفی $$X$$ وجود دارد.
• جابجایی بین عملگرهای مشتق و انتگرال امکان‌پذیر است.
• رابطه زیر برای هر نقطه از پارامتر برقرار است. به این معنی که گشتاور دوم مشتق تابع لگاریتم درستنمایی موجود بوده، مخالف صفر است.

$$\large \operatorname {E} \left[\left.\left({\frac {\partial }{\partial \theta }}\log f(X;\theta )\right)^{2}\right|\theta \right] >0$$

محاسبه اطلاع فیشر در حالت یک متغیره

تحت «شرایط نظم» (Regularity Conditions) که معرفی شده‌ است، می‌توان نشان داد،‌ امید ریاضی مشتق لگاریتم تابع درستنمایی نسبت به پارامتر $$\theta$$ براساس نمونه تصادفی $$X$$ صفر است. زیرا داریم:

$$\large \begin{aligned}\operatorname {E} \left[\left.{\frac {\partial }{\partial \theta }}\log f(X;\theta )\right|\theta \right]&=\int {\frac {{\frac {\partial }{\partial \theta }}f(x;\theta )}{f(x;\theta )}}f(x;\theta )\,dx\\&={\frac {\partial }{\partial \theta }}\int f(x;\theta )\,dx\\&={\frac {\partial }{\partial \theta }}1=0.\end{aligned}$$

در نتیجه جمله دوم از سمت راست رابطه ۱ صفر بوده و کافی است که فقط جمله اول را برای محاسبه واریانس بدست آوریم. این مقدار به عنوان اطلاع فیشر معروف است و بوسیله رابطه زیر محاسبه می‌شود.

$$\large I(\theta )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \theta }}\log f(X;\theta )\right)^{2}\right|\theta \right]=\int \left({\frac {\partial }{\partial \theta }}\log f(x;\theta )\right)^{2}f(x;\theta )\,dx$$

البته باز هم تحت «شرایط نظم» و با فرض وجود مشتق دوم برای تابع درستنمایی می‌توان شکل ساده‌تری برای محاسبه اطلاع فیشر نیز ایجاد کرد.

$$\large I(\theta )=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta ^{2}}}\log f(X;\theta )\right|\theta \right]$$

رابطه ۲

علت این امر آن است که براساس مشتق دوم لگاریتم تابع درستنمایی می‌توان رابطه‌های زیر را نوشت:

$$\large \frac {\partial ^{2}}{\partial \theta ^{2}}\log f(X;\theta )={\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}-\left({\frac {{\frac {\partial }{\partial \theta }}f(X;\theta )}{f(X;\theta )}}\right)^{2}=\\ \large {\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}-\left({\frac {\partial }{\partial \theta }}\log f(X;\theta )\right)^{2}$$

باز هم تحت شرایط نظم، امید ریاضی جمله اول سمت راست تساوی برابر با صفر است. زیرا با توجه به مفهوم و خصوصیت تابع چگالی احتمال و امکان جابجایی مشتق و انتگرال طبقه شرایط نظم، مقدار انتگرال زیر برابر با ۱ شده و مشتق مقدار ثابت برابر با صفر است. به این ترتیب امید ریاضی اولین جمله سمت راست تساوی بالا برحسب نمونه تصادفی (توزیع متغیر تصادفی $$X$$)، صفر خواهد بود.

$$\large \operatorname {E} \left[\left.{\frac {{\frac {\partial ^{2}}{\partial \theta ^{2}}}f(X;\theta )}{f(X;\theta )}}\right|\theta \right]={\frac {\partial ^{2}}{\partial \theta ^{2}}}\int f(x;\theta )\,dx=0.$$

در نتیجه کاملا مشخص است که با توجه به وجود شرایط نظم برای تابع چگالی متغیر تصادفی $$X$$ می‌توان اطلاع فیشر را به شکل ساده‌تری، مطابق با رابطه ۲، نوشت.

در ادامه به بررسی یک مثال برای متغیر تصادفی گسسته برنولی می‌پردازیم. البته در این مورد توجه داشته باشید که دامنه تغییرات برای پارامتر این توزیع زیرمجموعه‌ای از اعداد حقیقی است و با توجه به پیوستگی و مشتق‌پذیر بودن تابع درستنمایی یا چگالی احتمال برحسب پارامتر $$\theta$$ امکان جابجایی انتگرال و مشتق وجود دارد.

مثال ۱- اطلاع فیشر برای پارامتر توزیع برنولی

متغیر تصادفی برنولی را در نظر بگیرید. مشخص است که در این حال پارامتر $$\theta$$ احتمال موفقیت در نظر گرفته شده است. مقدارهای متغیر تصادفی نیز به صورت دو وضعیتی با ۰ برای شکست و ۱ برای موفقیت تعیین شده.

فیلم آموزش آمار ریاضی ۲ – آزمون فرض در فرادرس

کلیک کنید

با توجه به متغیر تصادفی برنولی، می‌دانیم امید ریاضی آن برابر با پارامتر $$\theta$$ است. حال اطلاع فیشر برای پارامتر $$\theta$$ به صورت زیر نوشته خواهد شد.

$$\large \begin{aligned}I(\theta )&=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta ^{2}}}\log \left(\theta ^{X}(1-\theta )^{1-X}\right)\right|\theta \right]\\&=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta ^{2}}}{\big (}X\log \theta +(1-X)\log(1-\theta ){\big )}\right|\theta \right]\\&=\operatorname {E} \left[\left.{\frac {X}{\theta ^{2}}}+{\frac {1-X}{(1-\theta )^{2}}}\right|\theta \right]\\&={\frac {\theta }{\theta ^{2}}}+{\frac {1-\theta }{(1-\theta )^{2}}}\\&={\frac {1}{\theta (1-\theta )}}.\end{aligned}$$

اگر یک نمونه n تایی از این متغیر تصادفی وجود داشته باشد، اطلاع فیشر برای چنین نمونه‌ای به صورت زیر در خواهد آمد.

$$\large I(\theta )={\frac {n}{\theta (1-\theta )}}$$

 رابطه ۳

همانطور که دیده می‌شود، این مقدار معکوس واریانس متغیر تصادفی برنولی با n بار تکرار است.

خاصیت زنجیره‌ای اطلاع فیشر

«اطلاع فیشر» برای دو متغیر تصادفی $$X$$ و $$Y$$ را می‌توان به دو بخش تفکیک کرد. به این تفکیک «خاصیت زنجیره‌ای» (Chain Rule) می‌گویند. فرض کنید که این دو متغیر تصادفی دارای توزیع توام باشند. آنگاه اطلاع فیشر این دو متغیر تصادفی به صورت زیر تفکیک می شود.

$$\large I_{X,Y}(\theta )=I_{X}(\theta )+I_{Y\mid X}(\theta )$$

توجه داشته باشید که منظور از $$I_{Y\mid X}(\theta )$$، اطلاع فیشر $$Y$$ نسبت به $$\theta$$ براساس تابع چگالی شرطی $$Y$$ با معلوم بودن $$X=x$$ است.

اگر دو متغیر تصادفی $$X$$ و $$Y$$ مستقل از یکدیگر باشند، رابطه به شکل ساده‌تری در خواهد آمد که در ادامه قابل مشاهده است.

$$\large I_{X,Y}(\theta )=I_{X}(\theta )+I_{Y}(\theta )$$

مشخص است که اطلاع توام متغیرهای $$X$$ و $$Y$$ به صورت جمع اطلاع فیشر هر یک نوشته شده است. بر همین اساس می‌توان اطلاع فیشر یک نمونه تصادفی nتایی (مستقل و هم توزیع) را به صورت جمع اطلاع فیشر هر یک از اعضای نمونه نوشت. این خاصیت را برای محاسبه رابطه ۳ به کار برده‌ایم.

ارتباط با کران پایین کرامر-رائو (Cramér–Rao bound)

حداقل ممکن برای واریانس برآوردگر توسط «کران پایین کرامر-رائو» (Cramér–Rao bound) بیان می‌شود. به این ترتیب اگر واریانس برآوردگری به کران پایین کرامر-رائو برسد، دیگر نمی‌توان آن را بهبود دارد و اگر کم بودن واریانس را ملاک انتخاب برآوردگر مناسب در نظر بگیریم، آن برآوردگری که واریانس آن برابر با کران پایین کرامر-رائو باشد، بهترین برآوردگر خواهد بود.

فرض کنید $$\theta$$ پارامتر جامعه و برآوردگر نااریب آن نیز $$\widehat{\theta}$$ باشد. اگر اطلاع فیشر برای این برآوردگر را با $$I(\theta)$$ نشان دهیم، می‌توان رابطه زیر را بین واریانس این برآوردگر و اطلاع فیشر نوشت.

$$\large \operatorname {Var} \left({\hat {\theta }}\right)\geq {\frac {1}{I\left(\theta \right)}}$$

به این ترتیب اگر واریانس برآوردگر یعنی $$\operatorname {Var} \left({\hat {\theta }}\right)$$ را به معنی دقت برآوردگر در نظر بگیریم، کران پایین برای آن معکوس اطلاع فیشر خواهد بود.

نکته: در اینجا کران پایین کرامر-رائو را برای برآوردگرهای نااریب (Unbiased Estimator) نوشته‌ایم. برآوردگرهایی نااریبی که واریانسی برابر با کران پایین کرامر-رائو داشته باشند، برآوردگرهای نااریب با کمترین واریانس یکنواخت (UMVUE- Uniform Minimum Variance Unbiased Estimator) گفته می‌شوند.

آماره بسنده و اطلاع فیشر

براساس تعریف «آماره بسنده» (Sufficient Statistic) می‌دانیم، بیشترین اطلاعات در مورد پارامتر، توسط آماره بسنده ارائه می‌شود. فرض کنید که $$X$$ نمونه تصادفی باشد، مشخص است که این نمونه تصادفی بیشترین اطلاعات را در مورد پارامتر دارد. اگر آماره بسنده برای پارامتر $$\theta$$ به صورت $$T(X)$$ نمایش داده شود، میزان اطلاعاتی که آماره بسنده در مورد پارامتر دارد برابر با نمونه تصادفی است.

اگر $$T(X)$$ یک آماره بسنده برای پارامتر $$\theta$$ باشد، می‌توان تابع چگالی احتمال برای متغیر تصادفی $$X$$ را به صورت زیر تجزیه کرد. این تجزیه به «معیار تفکیک نیمن» (Neyman's Factorization Criterion) مشهور است و به کمک آن می‌توان آماره بسنده را شناسایی کرد.

$$\large f(X;\theta )=g(T(X),\theta )h(X)$$

در این رابطه، $$g$$ تابعی برحسب $$T$$ (آماره بسنده) و پارامتر بوده ولی تابع $$h$$ فقط به نمونه تصادفی بستگی دارد. حال براساس این تفکیک، اطلاع فیشر را محاسبه می‌کنیم. از آنجایی که $$h(X)$$ به پارامتر بستگی ندارد، هنگام مشتق‌گیری از تابع درستنمایی حذف خواهد شد. در نتیجه خواهیم داشت:

$$\large \frac {\partial }{\partial \theta }\log \left[f(X;\theta )\right]={\frac {\partial }{\partial \theta }}\log \left[g(T(X);\theta )\right]$$

به این ترتیب به کمک این تساوی مشخص می‌شود که اطلاع فیشر حاصل از نمونه تصادفی با آماره بسنده برابر است. پس اطلاع فیشر براساس آماره بسنده نااریب $$I_{T(X)}$$، کران پایین برای واریانس هر برآوردگر نااریب دیگر مثل $$Z(X)$$ خواهد بود.

$$\large \operatorname {Var}(Z(X)) \geq \operatorname {Var}(T(X))$$

زیرا بین اطلاع فیشر هر یک از آن‌ها رابطه زیر برقرار است:

$$\large I_{Z(X)}(\theta )\leq I_{T(X)}(\theta )$$

ماتریس اطلاع فیشر (Fisher Information Matrix-FIM)

اگر توزیع آماری متغیر تصادفی $$X$$ دارای $$N$$ پارامتر باشد آنگاه بردار پارامتر به صورت  $$\theta ={\begin{bmatrix}\theta _{1},\theta _{2},\dots ,\theta _{N}\end{bmatrix}}^{\mathrm {T} }$$ نوشته شده و اطلاع فیشر برای این توزیع برحسب پارامتر، یک ماتریس $$N \times N$$ خواهد بود.

در این حالت ماتریس اطلاع فیشر (Fisher Information Matrix-FIM)  دارای عناصری به صورت زیر خواهد بود.

$$\large {\bigl [}{I}(\theta ){\bigr ]}_{i,j}=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \theta _{i}}}\log f(X;\theta )\right)\left({\frac {\partial }{\partial \theta _{j}}}\log f(X;\theta )\right)\right|\theta \right]$$

تحت شرایط خاص نظم، می‌توان عناصر ماتریس فیشر را به شکل ساده‌تری درآورد تا محاسبات راحت‌تر صورت گیرد. رابطه زیر جملات یا عناصر ماتریس فیشر را بر اساس مشتق دوم نمایش می‌دهد.

$$\large \big[{I}(\theta ){\bigr ]_{i,j}=-\operatorname {E} \left[\left.{\frac {\partial ^{2}}{\partial \theta _{i}\,\partial \theta _{j}}}\log f(X;\theta )\right|\theta \right]}$$

با کمی دقت متوجه خواهید شد که این رابطه درست به مانند رابطه مربوط به متغیر تک بعدی نوشته شده است.

به این ترتیب می‌توان «پارامترهای عمود برهم» (Orthogonal Parameters) را تعریف کرد. پارامترهای $$\theta_i$$ و $$\theta_j$$ را عمود بر هم گویند اگر عناصر سطر iام و ستون jام ماتریس اطلاع فیشر، صفر باشد. از آنجایی که صفر بودن این عناصر نشان دهنده مستقل بودن برآوردگرهای حداکثر درستنمایی این پارامترها است، به راحتی امکان بدست آوردن این برآوردگرها وجود دارد. به همین دلیل محققین به دنبال نشان دادن عمود بودن پارامترهای توزیع‌ هستند تا بتوانند با شیوه «حداکثرسازی تابع درستنمایی» (Maximum Likelihood Method)، برآوردگرها را محاسبه کنند.

مثال ۲- اطلاع فیشر برای پارامترهای توزیع چند متغیره نرمال

ماتریس اطلاع فیشر برای «توزیع نرمال چند متغیره» دارای شکل خاصی است. در این مثال به محاسبه و بررسی این ماتریس می‌پردازیم. فرض کنید که متغیر تصادفی $$X$$ دارای توزیع نرمال چند متغیره باشد، یعنی داریم $$X\sim N\left(\mu (\theta ),\Sigma (\theta )\right)$$. در اینجا بردار میانگین و ماتریس واریانس-کوواریانس، برحسب پارامتر $$\theta ={\begin{bmatrix}\theta _{1},\dots ,\theta _{K}\end{bmatrix}}^{\mathrm {T} }$$ نوشته شده‌اند. بنابراین ماتریس اطلاع فیشر (FIM) به صورت زیر در خواهد آمد.

$$\large I_{m,n}=\frac{\partial \mu^\mathrm{T}}{\partial \theta_m} \Sigma^{-1} \frac{\partial \mu}{\partial \theta_n} + \frac{1}{2} \operatorname{tr} \left(\Sigma^{-1} \frac{\partial \Sigma}{\partial \theta_m} \Sigma^{-1}\frac{\partial \Sigma}{\partial \theta_n} \right)$$

که در آن منظور از $$(.)^T$$، ترانهاده بردار و $$tr(.)$$ نیز «اثر ماتریس» (Trace) است. یعنی:

$$\large \frac {\partial \mu }{\partial \theta _{m}}={\begin{bmatrix}{\frac {\partial \mu _{1}}{\partial \theta _{m}}}&{\frac {\partial \mu _{2}}{\partial \theta _{m}}}&\cdots &{\frac {\partial \mu _{N}}{\partial \theta _{m}}}\end{bmatrix}}^{\mathrm {T} }$$

و همچنین برای ماتریس واریانس-کوواریانس نیز خواهیم داشت.

$$\large \frac {\partial \Sigma }{\partial \theta _{m}}={\begin{bmatrix}{\frac {\partial \Sigma _{1,1}}{\partial \theta _{m}}}&{\frac {\partial \Sigma _{1,2}}{\partial \theta _{m}}}&\cdots &{\frac {\partial \Sigma _{1,N}}{\partial \theta _{m}}}\\ \large {\frac {\partial \Sigma _{2,1}}{\partial \theta _{m}}}&{\frac {\partial \Sigma _{2,2}}{\partial \theta _{m}}}&\cdots &{\frac {\partial \Sigma _{2,N}}{\partial \theta _{m}}}\\ \large \vdots &\vdots &\ddots &\vdots \\ \large {\frac {\partial \Sigma _{N,1}}{\partial \theta _{m}}}&{\frac {\partial \Sigma _{N,2}}{\partial \theta _{m}}}&\cdots &{\frac {\partial \Sigma _{N,N}}{\partial \theta _{m}}}\end{bmatrix}}$$

نکته: اگر همه مولفه‌های ماتریس واریانس-کوواریانس برابر و بستگی به $$\theta$$ نداشته باشند، (یعنی داشته باشیم $$\Sigma (\theta )=\Sigma$$)، فرم اطلاع فیشر به صورت ساده‌تری در خواهد آمد. به رابطه زیر توجه کنید.

$$\large I_{m,n}=\frac{\partial \mu^\mathrm{T}}{\partial \theta_m}\Sigma^{-1}\frac{\partial \mu}{\partial \theta_n}$$

کاربردهای اطلاع فیشر

در «آمار بیز» (Bayesian Statistics) اگر هیچ اطلاع یا توزیعی پیشینی برای پارامتر $$\theta$$ نتوان در نظر گرفت، از توزیع «پیشین جفریز» (Jeffreys Prior) که برحسب اطلاع فیشر محاسبه می‌شود، استفاده می‌کنند. پیشین جفریز را به عنوان پیشین استاندارد یا پیشین «بدون اطلاع» (Non-informative) برای توزیع‌های پیوسته در نظر می‌گیرند.

همچنین از اطلاع فیشر در تکنیک‌های «یادگیری ماشین» (Machine Learning) مانند روش «تثبیت وزن‌های الاستیک» (Elastic Weight Consolidation) که به اختصار EWC نامیده می‌شود، بهره می‌برند.

در مسائل «طرح آزمایشات» (Experimental Design) از اطلاع فیشر استفاده می‌شود. زیرا برحسب نسبت واریانس برآوردگر و اطلاع فیشر، می‌توان با حداقل کردن واریانس نسبت به حداکثر کردن اطلاع فیشر، برآوردگر مناسب را پیدا کرد. در آزمون همزمان والد نیز ماتریس اطلاع فیشر به کار رفته و در انجام محاسبات مربوط به این آزمون به کار گرفته می‌شود.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• آموزش آمار و احتمال مهندسی
• آزمایش تصادفی، پیشامد و تابع احتمال
• مجموعه آموزش‌های نرم‌افزارهای آماری
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^